考虑材料参数不确定性的皮肤伤口缝合力预测模型*

温广全, 纪小刚,2, 段玉顺, 邓 霖

(1. 江南大学 机械工程学院, 江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122)

0 引 言

皮肤伤口缝合作为临床医生的必备技能,是外科手术治疗的重要环节．随着科学技术的进步,机器人手术缝合技术得到快速发展[1],拓展了外科医生的诊断治疗能力．对于机器人手术缝合过程,力觉信息对其缝合效果的影响至关重要[2],了解闭合伤口所需缝合力对机器人缝合算法的开发具有重要的指导作用[3]．

近年来,数值仿真技术已成为研究皮肤等生物软组织力学响应的强大工具[4],可有效地用于预测闭合伤口所需的力[5]．然而,皮肤等生物组织材料具有一定的特殊性及复杂性[6],材料模型往往难以与皮肤真实的力学响应完全匹配[7]．尽管现在各国学者提出了一些更为复杂,针对性更强的材料模型[8-9],大大提高了模型的准确性和预测能力,但材料参数的确定依赖实验数据的准确性与多样性,且材料特性受年龄、性别、身体部位等因素影响具有较大的差异性[10],这就造成数值计算过程存在输入材料参数的不确定性,如不加以考虑,可能会导致计算结果产生波动甚至偏离预期[11]．为了严格评估材料参数的不确定性对伤口缝合力预测结果的影响,亟需一套不确定性传播分析方法．

决策和优化过程中,不确定性传播分析在减少不确定性的影响方面起着关键作用,已被应用于解决科学和工程领域的各种现实问题[12]．然而,很少有针对皮肤组织数值计算不确定性问题的相关研究．为了得到可靠的伤口缝合力预测结果,如何在充分了解皮肤力学特性的基础上,量化影响皮肤伤口缝合数值计算结果的不确定性材料参数,进一步获取材料参数不确定性影响下皮肤伤口缝合力的概率统计信息,是亟需解决的问题．Monte-Carlo(MC)方法[13]结合代理模型技术[14]为此问题的解决提供了有效的思路．MC方法因构造简单,在不确定性传播分析中应用广泛[15]．而代理模型通过构建一个数学表达式来描述输入变量和输出响应之间的关系,只需要运行有限数量的仿真计算,便可得到宽泛参数空间下的预测结果,用于解决MC方法对计算资源需求大的问题[16]．同时通过使用光滑连续的插值函数,代理模型可以有效减少数值计算过程产生的噪声．常用的代理模型方法有响应面模型、Gauss过程回归和人工神经网络[17]等．其中,人工神经网络方法具有近似复杂非线性函数的能力、极好的泛化能力,在预测材料的力学响应方面具有一定的优势[18]．

本文基于皮肤组织结构及力学特性,通过文献归纳及相关皮肤力学试验,获取了大量构建不确定性皮肤伤口缝合力预测模型所必需的力学参数信息．然后将椭球基(elliptical basis functions, EBF)神经网络代理模型方法与有限元方法、MC方法相结合,构建出皮肤伤口缝合力预测模型．最后分析了皮肤材料参数的不确定性对计算结果的影响,并通过实验对预测结果进行验证,以期为机器人手术缝合提供可靠的力学参考数据．

1 皮肤伤口缝合力数值计算

1.1 皮肤材料本构模型

皮肤结构从上到下分为表皮层、真皮层和皮下组织,其中真皮层是主要承载层,由嵌在基质中的纤维网络组成．在力学上,皮肤表现出非线性的应力-应变响应特性,且在很小的外力下即可产生较大的变形,Holzapfel超弹性本构模型可以很好地描述其力学行为[8-9]．其应变势能函数为

(1)

(2)

应变能函数中C10,k1,k2,D,κ是有限元分析的输入参数．其中,C10与材料的剪切模量相关,反应皮肤非胶原纤维部分的组织刚度;k1代表皮肤纤维的刚度模量;k2为无量纲参数,反应组织的非线性力学性能;D与材料的体积模量相关,参数κ(0<κ<1/3)描述了皮肤纤维方向的分散程度,κ= 0纤维完全对齐,κ= 1/3纤维随机分布,材料呈各向同性．

1.2 皮肤伤口有限元模型

使用ABAQUS有限元分析软件对皮肤伤口进行建模计算．伤口轮廓如图1所示．皮肤组织被简化为100 mm×100 mm的平面,伤口形状被定义为纺锤形,尺寸由长短轴确定．长轴a固定为40 mm,短轴b分别取5 mm,10 mm,15 mm,20 mm,模型厚度t参考人体皮肤厚度范围[4]分别取1.5 mm,2 mm,2.5 mm,3 mm,3.5 mm,4 mm．缝合间距取5 mm,伤口共计需缝合7次,缝合点位置如图1所示．

图1 皮肤伤口轮廓 图2 皮肤伤口有限元简化模型 Fig. 1 The skin wound profileFig. 2 The simplified finite element model for the skin wound

考虑到模型的对称性, 取伤口的二分之一进行分析．短轴b与厚度t排列组合, 24种伤口尺寸模型被创建．皮肤组织采用Holzapfel超弹性本构模型,C10,k1,k2,D,κ是需要输入的材料参数．鉴于皮肤软组织通常被认为是近似不可压缩的[19],同时为了保证所有输入参数的收敛,D被固定为0.2．在分析中,假设κ= 1/3,皮肤表现为各向同性．虽然皮肤的确表现出各向异性,但纤维色散相对较大[20],随机纤维色散是一种合理的近似．以往关于皮肤力学特性的研究[10, 20],为人体皮肤本构模型参数C10,k1,k2提供了合理的取值范围,归纳如表1所示．此外,由于活体皮肤正常情况下处于张力状态[4],为得到皮肤组织中力学响应更真实的预测,分别在平面模型X,Y方向横截面上施加预应力σX,σY,取值参考文献[5],归纳如表1所示．为了模拟手术缝合过程,减少建模过程对分析结果的影响,模型统一采用八节点线性六面体单元,根据缝合间距统一单元尺寸为5 mm．通过设置7个静力通用分析步,在伤口边缘节点处逐次施加线性位移约束,以模拟伤口的闭合．有限元简化模型如图2所示．有限元计算结果为7个分析步中,施加位移约束节点的反力,记为F1～F7,以此作为伤口缝合过程中缝合线对伤口边缘的缝合力．

表1 人体皮肤材料参数取值范围

2 皮肤伤口缝合力预测模型构建

2.1 样本数据的获取

以尺寸及材料参数的不同组合得到的皮肤伤口缝合力数值计算结果,作为构建皮肤伤口缝合力预测模型的样本数据．考虑表1获取的材料参数可能存在误差,本文将表1的参数范围进一步扩展20%,以便在较大参数范围内训练代理模型后,用来传播更小范围的、真实的参数联合概率分布信息．

为充分探索整个材料参数范围对输出结果产生的响应,采用优化拉丁超立方采样方法,创建了基于参数b,t,σX,σY,C10,k1和k2的2 000组不同组合,总共进行了2 000次仿真计算．本文首先随机抽取1 400组仿真数据用来构建代理模型,剩余600组数据用作验证数据集,以校验代理模型的拟合精度．

2.2 EBF神经网络模型的构建

EBF神经网络模型采用椭圆单元隐层和线性单元输出层,来描述输入变量和输出响应之间的关系．本文所构建的EBF神经网络模型基本结构如图3所示．其中输入层的x1～x7分别代表伤口尺寸b,t和材料参数σX,σY,C10,k1,k2,输出层的y1～y7分别代表有限元输出结果F1～F7．

图3 EBF神经网络基本结构Fig. 3 The basic structure of the EBF neural network

设输入层中变量个数为N,隐含层样本数为n,输出层响应变量个数为M．以待测点与样本点之间的Mahalanobis距离为自变量,通过线性叠加构造出EBF神经网络模型,其响应函数表达式如下:

(3)

式中,gi(x)为基函数,由式(4)给出

gi(x)≡g(‖x-xi‖m),i=1,2,…,N,

(4)

‖x-xi‖m=(x-xi)TS-1(x-xi),

(5)

(6)

式中,‖x-xi‖m是待测点与样本点之间的Mahalanobis距离,S为多维随机变量的协方差矩阵,μ为样本中心点．

式(3)中αi为权重系数,通过求解式(7)线性方程组求得

(7)

2.3 不确定性传播分析

构建好代理模型后,除了无需在特定输入上重新进行有限元计算便可得到预测结果外,还可以进行不确定性传播分析．本文将采用MC方法进行皮肤伤口缝合力预测中的材料参数不确定性问题分析．

MC方法也称统计试验方法, 是以概率统计理论为基础的一种数值计算方法．其基本思想是, 当想要获取某个随机变量的期望值时, 可以采用抽样试验或随机模拟的方法, 得到这个随机变量的平均值, 以此作为问题的解．

本文实现步骤为:

1) 假设皮肤材料参数围绕实验测量或经验评估结果呈正态分布,根据获取材料参数的可靠程度,给出参数的不确定度．本文统一设为±10%．

2) 采用描述抽样方法,抽取10 000个样本点,通过代理模型快速得到缝合力输出响应结果．需要强调的是,MC方法统计结果的准确性非常依赖于样本数据的规模,规模越大样本统计特性越优越,因此,在计算资源足够的情况下,应抽取尽可能多的样本数据．

(8)

(9)

其中,Q为抽样容量,yi(i=1,2,…,Q)为样本输出变量的响应值．

4) 计算输出结果总体均值的置信区间:

(10)

式中,zα/2为标准分数,置信水平为100(1-α),α通常取值0.1或0.05．

气象信息化建设是一项持续性的工作,对于基层气象部门来说,信息化基础设施构建要按照上级气象部门的统一部署,符合中国气象局《气象信息化发展规划(2018—2022年)》构建统筹集约、协同高效、开放共享、安全可靠的气象信息化体系的总体目标,在此基础上广泛应用成熟、先进的信息化技术、同时参考本地区气象部门经过实践检验,广泛应用的技术规范,以便和本地区气象部门顺利对接,逐步探索符合当地气象业务特点的气象信息化建设思路和建设模式,以期为提高本地区气象灾害监测防御能力,预防和减轻气象灾害损失,保障人民生命财产安全,促进当地经济社会健康发展提供强有力的保障。

3 案 例 分 析

文献表明,猪皮肤生理结构和力学特性与人体相似[21]．本文以普通家猪腹部皮肤组织为研究对象,通过实验测量缝合伤口所需的力,并与预测模型进行比较,以验证模型的可靠性．实验均在同一环境下进行,未考虑温度、湿度等外在因素的影响．

3.1 皮肤材料参数获取

由于缺乏家猪皮肤的材料参数信息,本文设计了两个实验来进行评估．需要获取的材料参数有:皮肤本构模型参数和皮肤预应力参数．

图4给出了通过试验最终得到的真实应力-应变曲线．为获取皮肤本构模型参数,我们制作了图4所示的厚度为3 mm的板状皮肤拉伸试样,试样取自五个月大、重约120 kg的普通家猪腹部．使用CTM2500万能材料试验机(最大荷重为10 kN,荷重精度为±0.01%,精度等级为0.5级,位移分辨率为0.03 μm)对试样进行单轴拉伸试验．试验采用楔形夹具,夹具与皮肤组织接触处有许多整齐的小齿,可以有效增大夹爪与皮肤组织之间的摩擦因数,避免试样在拉伸的过程中发生滑移．应变测量采用标距为25 mm,量程为25 mm的引伸计．根据大变形后体积V不变的假设,即A0L0=AL,真实应力σ=F/A=FL/(A0L0);真实应变ε=ln(L/L0)．其中,F为拉伸载荷,A0,A分别为试样初始及任一瞬时的横截面积,L0,L(L=L0+ΔL)分别为初始标距和任一瞬时的标距．由真实应力-应变曲线拟合得到皮肤的本构模型参数为C10=24.22 kPa,k1=24 421 kPa,k2=369.7．

图4 猪皮单轴拉伸试样尺寸、试验设备及应力-应变曲线Fig. 4 Sizes, the test equipment and the stress-strain curve of the pig skin uniaxial tensile test specimen

为获取皮肤预应力信息,参考金属构件残余应力测量方法[22],从普通家猪腹部切取100 mm×100 mm皮肤组织试样进行实验．由于预应力释放,切取的皮肤组织轮廓产生尺寸收缩．假设尺寸收缩是由皮肤预应力弹性释放造成的,并且皮肤横截面在预应力释放过程中产生等变形收缩．如果施加外力将变形后的皮肤组织恢复到切割前的状态,所得到的截面应力就等效于切割前该截面的预应力．基于此,采用弹性有限元方法,计算皮肤轮廓恢复到切割前的应力状态．具体步骤如下:

1) 在ABAQUS中以收缩后的试样尺寸建模,鉴于模型的对称性,取皮肤组织四分之一进行建模,并采用八节点线性六面体单元划分网格;

2) 本构模型参数采用上述单轴拉伸试验结果;

3) 模型边界施加对称约束并限制底面Z向位移,切割横截面上施加位移约束使试样尺寸变为初始尺寸100 mm×100 mm,如图5(a)所示;

3.2 伤口缝合力测量

在普通家猪腹部分别设计了40 mm×10 mm和40 mm×14 mm、厚度为3 mm的各3组皮肤伤口;使用精度为0.01 N,型号为AIPLI-SF-10的电子拉力计测量闭合伤口所需的力;采用单纯间断缝合法闭合伤口,缝合线两端水平对齐,同时拉动两端缝合线,使伤口边缘沿中轴线紧密对齐;重复测量,记录均值与标准差,伤口尺寸及缝合力测量方法如图6所示,两种伤口缝合力测量结果如图7所示．其中横坐标1～7代表伤口的7个缝合点,其位置如图1所示,纵坐标为该点缝合力测量结果．

(a) 边界条件 (b) 横向预应力 (c) 纵向预应力 (a) Boundary conditions(b) Transverse prestresses (c) Longitudinal prestresses图5 皮肤组织预应力释放的反向模拟边界条件及计算结果Fig. 5 Boundary conditions and calculation results of the reverse simulation of prestress release in the skin tissue

图6 伤口尺寸及缝合力测量方法Fig. 6 Measurement of wound sizes and suture forces

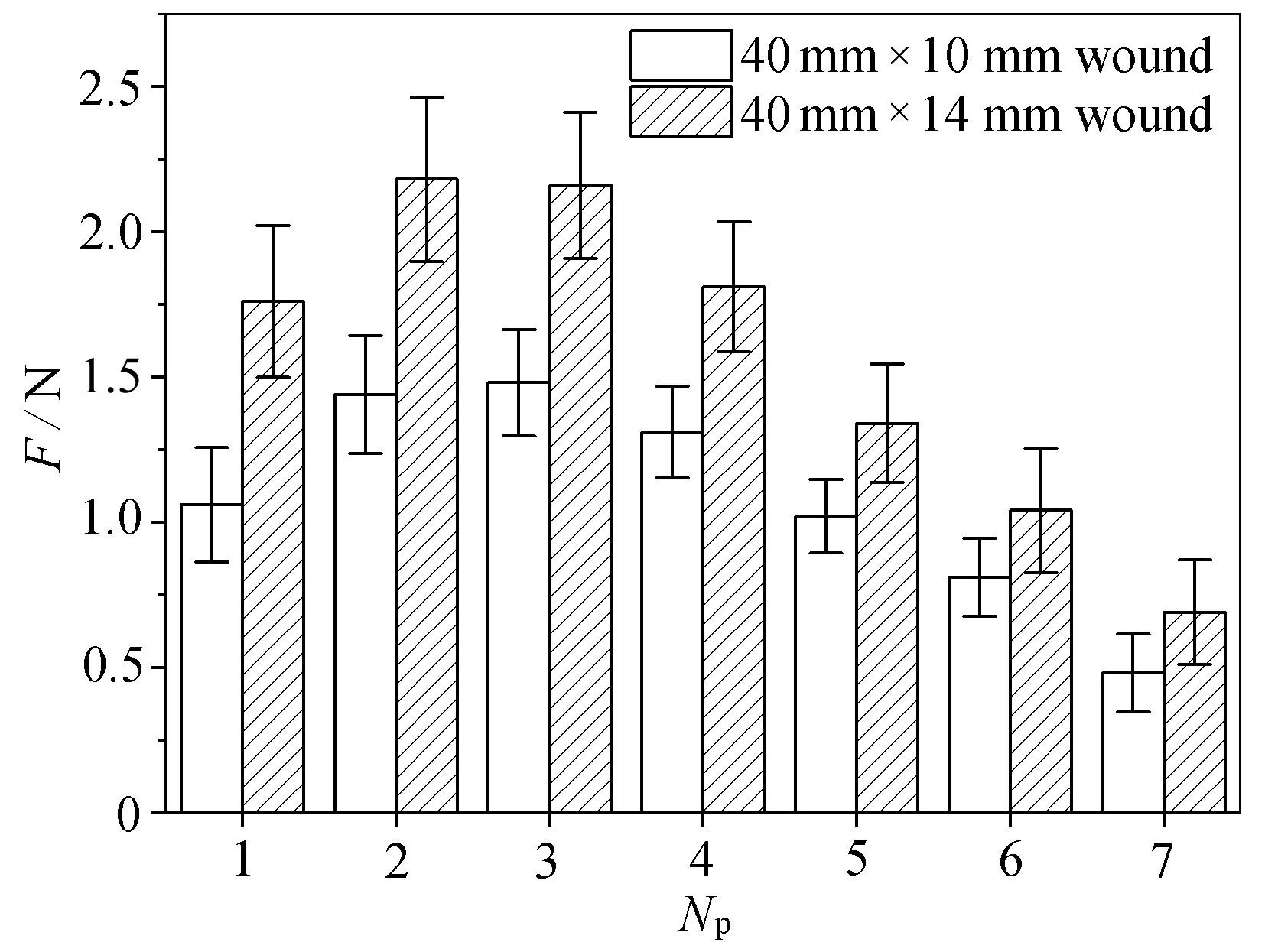
图7 伤口缝合力测量结果Fig. 7 Wound suture force measurement results

3.3 模型预测结果统计分析

材料参数取实验估计值时,40 mm×10 mm伤口缝合力有限元计算结果如图8所示．其中图8(a)为伤口施加预应力后的初始状态,图8(b)—(h)为缝合过程．可以看出施加位移约束节点处,即缝合点处力最大,并且7个缝合点处缝合力大小按缝合针次依次呈先增高后逐渐降低趋势,缝合力大小在0～1.5 N之间,与图7实验测量结果接近．

图8 有限元模拟缝合过程Fig. 8 The finite element simulation of the suture process

构建的EBF神经网络模型需要进行校验,本文采用式(11)的决定系数R2来评估所构建代理模型的拟合精度:

(11)

图9 3种代理模型拟合精度 图10 输出响应概率分布图 Fig. 9 The fitting precision of 3 proxy modelsFig. 10 The output the response probability distribution graph

输入测得的猪皮材料参数及伤口尺寸参数,通过构建的皮肤伤口缝合力预测模型,计算得到各输出变量的概率密度分布、均值以及标准差．以40 mm×10 mm伤口中心节点处缝合力F4的统计结果为例,得到输出响应的概率分布,如图10所示．可以看出,结果呈现出良好的正态分布,表明参数样本具有良好的统计特性,同时受材料参数不确定性影响,伤口缝合力预测结果表现出较高的离散性．

模型预测结果与实验测量结果的对比如图11所示．结果显示,采用间断缝合椭圆形皮肤伤口,所需缝合力呈先增后减趋势,峰值力发生在伤口中线前．40 mm×10 mm伤口缝合力峰值约为1.7 N;40 mm×14 mm伤口缝合力峰值约为2.5 N．受材料参数不确定性影响,缝合力预测结果最大有±0.6 N的波动,随着所取置信水平的增大,模型预测结果的置信区间变大,绝大部分实验测量结果落在95%置信区间范围,少数结果超出这一范围,所有测量结果均落在90%置信区间范围,相比于单纯地进行一次仿真计算,考虑了参数的不确定性后得到的结果更加稳健可靠．从40 mm×14 mm伤口对比结果可以看出,对于建模尺寸外的伤口,预测模型亦有较好的预测效果．决策者可以根据不同的精度要求,选择相信不同置信水平对应的缝合力置信区间,作为机器人缝合算法的参考输入．

(a) 40 mm×10 mm伤口 (b) 40 mm×14 mm伤口 (a) 40 mm×10 mm wound (b) 40 mm×14 mm wound图11 伤口缝合力预测结果与实验测量结果对比Fig. 11 The prediction results of wound suture forces compared with the experimental results

4 结 论

本文应用有限元理论对皮肤伤口缝合过程进行力学仿真计算,并将代理模型方法及MC方法结合,得到了考虑皮肤材料参数不确定性的皮肤伤口缝合力预测模型．通过与普通家猪皮肤伤口缝合实验结果相比较,验证了模型的可靠性．

此外,皮肤材料实际上还表现出黏弹性、可压缩性、各向异性等材料力学特性,本文方法为分析皮肤等生物软组织数值仿真不确定传播问题提供了一般思路,额外考虑皮肤的黏弹性、可压缩性、各向异性,并与皮肤力学特性在体测试技术相结合,将得到更加准确的预测结果．同时该方法还可以扩展到更广泛的伤口尺寸及形状,期望能为机器人手术缝合算法的开发及术前指导提供参考依据．