基于键型近场动力学非连续Galerkin有限元法的爆炸毁伤模拟*
成嘉禾, 顾 鑫, 章 青
(河海大学 力学与材料学院, 南京 211100)
0 引 言
随着全世界范围内因政治、经济和宗教等因素引发各类型爆炸事故的发生,国内外对爆炸研究的关注度有所提升[1].爆炸荷载作为一种非常规极端荷载,以其传播迅速、峰值大、作用时间短以及具有负超压等特点[2],极易导致目标结构发生灾变破坏,造成严重的人员伤亡和经济损失[3].为了确保结构安全,研究爆炸荷载作用下结构的毁伤破坏效应,进而揭示爆炸毁伤破坏的作用机制,具有重要意义.
目前,数值计算与仿真技术在结构爆炸毁伤模拟中发挥重要作用[4].Ruwan等[5]针对钢筋混凝土框架进行爆炸荷载数值模拟,研究了框架结构在爆炸荷载作用下的倒塌机制;Xu等[6]基于ANSYS/LS-DYNA对爆炸荷载作用下钢筋混凝土板产生的碎片进行模拟分析;朱劲松等[7]采用ALE算法,模拟了炸药爆炸后桥梁结构的动态响应和毁伤失效过程.上述数值模拟方法大都建立在经典连续介质力学基础上,在求解裂纹等不连续处的微分方程时遭遇奇异性困扰[8],不能自发地模拟裂纹的生成、扩展,也无法直接描述碎块形成与剥离的过程,模拟结构爆炸毁伤的能力尚有不足.
近场动力学(peridynamics, PD)[9-12]兼具连续介质力学和分子动力学的特点,作为一种新兴的积分型非局部连续介质力学方法,通过求解空间内一系列包含物性信息的物质点的运动方程组,以描述材料的变形和破坏过程,在固体破坏问题分析中具有独特优势[13].近场动力学主要采用强形式方程的无网格粒子类显式动力学方法进行求解[14-15],该类解法要求结构离散为高密度的均匀离散点阵,离散粒子或结点数量众多,计算效率低,且相比于传统局部有限元方法,近场动力学方法还存在表面效应问题与自然边界条件施加的困难.
近年来,弱形式近场动力学方程的非连续Galerkin有限元方法得到发展[16-18].非连续Galerkin有限元法通过形函数插值构建单元内连续的位移场,采用分段连续位移场代替近场动力学的位移近似场,再求解弱形式的近场动力学方程,在有限元框架内实现基于近场动力学理论的数值计算,以充分利用有限元法的通用高效求解器.需要指出,局部模型的非连续Galerkin有限元方法需要额外设定单元间的数值通量限制条件[19],但在近场动力学理论中,通过各离散点之间的键建立了单元间的连通性,无需增加额外的限制条件.该方法采用Gauss积分点进行积分运算,既放松了有限元法对位移解连续性的要求,又保持了有限元格式,还继承了有限元法能直接施加局部边界条件、约束和接触条件以及适应非均匀网格的优点,并可以通过修正边界附近积分点上键对应的微弹性模量,确保整体材料等效性能的均匀分布,可有效避免传统近场动力学方法的表面效应问题.2011年,Chen等[20]开创性地将非连续Galerkin有限元法应用于近场动力学模型,并求解了一维问题;Aksoy等[21]利用非连续Galerkin有限元法构建了键型近场动力学的控制方程;2015年,键型近场动力学的非连续Galerkin有限元法被置入大型商业软件LS-DYNA中;Ren等[22-23]将该方法应用于脆性材料和纤维增强复合材料的破坏分析中.但总体来看,国内外现有文献对于近场动力学非连续Galerkin有限元方法的数值实施方案描述不够清晰,缺少具体算法细节,且鲜有大变形破坏问题的研究成果报道.
本文阐述了键型近场动力学的非连续Galerkin有限元法的算法细节,计算模拟了脆性玻璃板动态开裂过程中的裂纹分叉问题.在此基础上,采用该方法对爆炸冲击荷载作用下混凝土板的毁伤过程进行了建模分析,获得了混凝土板损伤产生、裂纹扩展直至破坏的全过程,为结构爆炸毁伤过程的破坏模拟提供了新的途径.
1 键型近场动力方程及其弱形式
近场动力学将研究对象离散为一系列物质点,采用空间积分型运动方程描述物质点的运动和变形,物质点的受力变形等状态取决于该点与其所在的有限空间内其他物质点间的非局部相互作用.考虑三维空间中的计算域Ω∈R3,对于任一物质点X与其周围一定范围内的其他物质点X′∈Ω:‖X′-X‖≤δ,在时刻t存在相互作用力,则近场动力学运动方程为
(1)
其中,ρ为物质密度,u为物质点位移矢量,HX表示以δ为半径的近场邻域,f为物质点X和点X′的近场动力学键力密度函数,b为体力密度函数,VX′为物质点体积.
在键型近场动力学中,对于均匀微观弹性材料,物质点间“键”所蕴含的能量密度ω与键力密度函数满足如下关系[14]:
(2)
式中,ξ=X′-X为两物质点的相对位置,η=u(X′,t)-u(X,t)表示两物质点的相对位移.
键型近场动力学中的微观弹性材料可以是各向同性或各向异性材料,经典微弹脆性(prototype micro-brittle, PMB)材料是线性各向同性的,其能量密度ω可以表征为[14]
(3)
式中,c=18k/(πδ4)是微弹性模量[22],k为体积模量;s=(|η+ξ|-|ξ|)/|ξ|表示键的伸长率,则物质点间的键力密度函数为[14]
(4)
材料的损伤通过物质点之间的相互作用进行描述,当“键”的伸长率s超过了其临界值s0时,“键”断开,损伤发生,相应的键力将不可逆地永久消除[15].临界伸长率s0与经典断裂力学中的断裂能释放率Gc有关,基于能量守恒原理,可以求得三维键型近场动力学模型的临界伸长率[22],具体为
(5)
当物质点X具有完整近场邻域HX(X,δ)时,通过假设物质点的弹性能密度与其所有键在各向同性变形条件下的应变能密度相等,建立刚度系数与微弹性模量之间的等效关系[22]:
(6)
式中,E为弹性模量.为满足弹性能密度与应变能密度的一致性,根据式(6)的等效关系,人为修正边界周围物质点间键的微弹性模量,从而确保整体材料等效性能的均匀分布,避免近场动力学的表面效应问题,具体为椭球体校准算法,通过键之间的球坐标关系校正微弹性模量,可参考文献[24].
式(1)的解属于受限的Banach空间,记计算域Ω的位移边界为Su,位移解u和权函数v定义在L2函数空间内,即
(7)
其中,S(Ω)为Banach仿射空间,S′(Ω)为子空间,Xg为Gauss点坐标,g(Xg)为Gauss点在位移边界的已知值.
运动方程两端同乘以权函数矩阵v(X)后,在求解域内积分,得到积分弱形式的控制方程:
∀u(X)∈S(Ω),v(X)∈S′(Ω).
(8)
2 键型近场动力学的非连续Galerkin有限元方法
如图1所示,传统有限元域相邻单元共享节点,而非连续Galerkin有限元法离散采用非连续网格,即相邻单元间不共用节点,以反映非连续变形效应,则节点总数等于所有单元的节点数之和.

图1 传统有限元的连续网格(左)与非连续Galerkin有限元的网格(右)[22] Fig. 1 The continuous mesh of traditional finite elements (left) and the mesh of non-continuous Galerkin finite element (right) [22]
类似于连续Galerkin有限元法[25],位移解u(X)和权函数v(X)分别由形函数插值得到
u(X)=N(X)d,v(X)=N(X)vi,
(9)
式中,d为单元节点位移列向量,vi为节点对应的权函数列向量.
将求解域Ω划分为若干个单元,并选择单元体积Ωe作为积分域,将近似解和权函数代入近场动力学积分弱形式方程(8),可得到
(10)
对上式中的积分进行离散化处理,即可得到离散化的弱形式方程:
(11)

将式(11)中的相关项记为单元质量矩阵Me和单元荷载列阵Fe,即
(12)
需要指出的是,上式推导不包含边界单元的情形.当涉及到边界单元求解时,由于近场动力学的自然边界条件施加不同于传统的有限元法,需要将面力转化为体力密度施加于边界物质点上,通过形函数插值实现单元表面面力到Gauss点体力密度的转换,并保持有限元格式,即
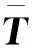
为简便计,Gauss点Xg的初始位置矢量也记为Xg,这个位置矢量和位移矢量ug可由所属单元节点列向量插值得到,分别为
(13)

于是,Gauss点的相对位置和相对位移为
(14)
分别使用i,j(i=1,2,…,n;j=1,2,…,ng′)表征Gauss点Xg,Xg′,可以将相对位移表示为矩阵形式:
ηji(Xg,Xg′)=Njdj-Nidi=[Nji][dji],
(15)

根据近场动力学PMB模型线性化后的键力密度函数表达式,经推导后不难得到Gauss点间键力的矩阵形式[24]:
(16)
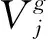
这样,式(11)右端第一项可改写为
(17)
在计算域内,对Gauss点i=1,2,…,n的近场范围内的所有Gauss点j=1,2,…,ng′进行二重循环求和,可以求得单元劲度矩阵,再按照总体节点编号进行组装,即可形成整体劲度矩阵K.再将单元质量矩阵与单元荷载列阵进行整体组装,得到整个系统的运动方程:
(18)
相应的静力平衡方程表示为
[K]3N×3N[U]3N×1+[Fe]3N×1=0.
(19)
至此,根据式(18)和(19),施加边界条件后即可求解整个系统方程.由于近似场是通过传统的有限元形函数构造的,所以边界条件可由有限元法的标准形式执行.对于应力边界条件,面力可直接转化为等效节点荷载; 对于位移边界条件,可将其表示为约束方程GU+U*=0,其中G为约束方程系数矩阵,与未知位移向量U相关,U*为已知位移约束值构成的列阵.引入Lagrange乘子法λ,对系统平衡方程和约束方程的混合变分形式进行重构,得到求解U和λ的代数方程组:
(20)
该方程组可采用MKL英特尔数学核心函数库提供的大型稀疏方程组求解器PARDISO或GMRES等求解.
3 算 例 分 析
3.1 玻璃板的动态裂纹扩展模拟
如图2所示,含预制裂纹玻璃板的长度为100 mm,宽度为40 mm,左端预制裂纹长50 mm.玻璃板[26]的材料参数为:弹性模量E=72 GPa,密度ρ=2 240 kg/m3,能量释放率Gc=135 Ν/m,Poisson比μ=0.25.板的上下两端受均匀拉伸应力载荷σ=14 MPa作用,持续时间为t=5×10-5s.

图2 含预制裂纹玻璃板及其外荷载Fig. 2 The pre-cracked glass panel and its external load
采用基于键型近场动力学的非连续Galerkin有限元方法对上述问题进行求解.考虑Δx=1 mm,0.5 mm,0.25 mm三种不同的物质点间距,近场范围为δ=3 mm,显式动力求解的时间步长取为Δt=2.5×10-8s.Ha等[26]采用基于均匀粒子离散的传统键型近场动力学方法对该问题进行了模拟计算,但应力边界条件进行了特殊处理.图3和图4分别给出了本文方法和Ha等[26]计算得到的裂纹扩展结果,从所示结果可以看出,三种不同物质点间距的结果均能反映玻璃板的裂纹萌生、扩展过程,只是当物质点间距为Δx=1 mm时裂纹扩展路径较为粗糙,本文得到的裂纹扩展路径和裂纹分叉特征与Ha等[26]的结果非常相似,物质点间距的不同对裂纹分叉点的位置几乎没有影响,但间距过大会使得裂纹扩展路径不够平顺.

(a) Δx=1 mm

图4 本文方法(上)与Ha等[26]方法(下)得到的裂纹在分叉点演变情况Fig. 4 The evolution of crack bifurcation points obtained with the present method (top) and the method of Ha et al.[26] (bottom)
为了比较基于键型近场动力学的非连续Galerkin有限元方法与传统键型近场动力学方法的计算效率,本文还采用Ha等[26]的方法对上述问题进行了模拟计算,两种方法的物质点间距和近场范围等计算条件均保持相同.表1给出了本文方法与传统键型近场力学方法的计算时间对比情况,表明本文方法相较于传统键型近场力学方法在计算效率上有较大提升.

表1 计算时间对比
3.2 三维混凝土板的爆炸模拟
三维素混凝土板的长度、宽度和厚度分别为1 m,1 m和40 mm[27],考虑在板的中心正上方有TNT炸药发生爆炸.采用本文的基于键型近场动力学的非连续Galerkin有限元方法进行计算模拟,研究板的边界条件、爆距和炸药当量对混凝土板毁伤破坏模式的影响.材料参数为:密度ρ=2 750 kg/m3,弹性模量E=38.2 GPa,临界断裂能释放率Gc=120 J/m2,Poisson比μ=0.25.采用八节点六面体单元离散混凝土板,在板的长、宽和厚度方向上,单元网格尺寸分别为10 mm,10 mm和8 mm.
对于爆炸荷载,本文采用美国陆军技术手册TM5-855-1提供的Kingery-Bulmash经验公式[28],将TNT炸药爆炸后产生的冲击波直接施加到混凝土板迎爆面所有单元表面上,考虑了入射压力和反射压力等的作用,具体为
P(t)=Pr(t)cos2θ+Pi(t)(1+cos2θ-2cosθ),
(21)
式中,P为施加到单元表面上的压力值;θ为入射角,即单元上表面中心和爆源连线与单元法线的夹角;Pi为入射压力,Pr为反射压力,可表示为
(22)
式中,Pio和Pro分别为入射压力峰值和反射压力峰值,与炸药性能、炸药当量、冲击波荷载作用点与爆炸中心的距离等有关,可参考文献[28],a和b为衰减系数,to为正压作用时间,同样可参考文献[28].
3.2.1 不同边界条件对混凝土板毁伤的影响
考虑两种边界条件,一种是对边固定,另一种是四边固定,相应的几何模型如图5所示.爆炸中心距离混凝土板的上表面中心0.4 m,TNT炸药当量为0.15 kg.

图5 左右两边固定约束(左)与四周固定约束(右)的几何模型Fig. 5 Geometric models with fixed constraints on the left and right sides (left) and fixed constraints on all sides (right)
以炸药起爆时刻为零点,图6给出了对边固定条件下混凝土板受爆炸冲击载荷作用后不同时刻的毁伤情况.在0.9 ms时刻,由于左右两边固定边界的混凝土板迎爆面和背爆面的对边边界内缘处均出现裂纹,迎爆面裂纹更长,已逐渐延伸至混凝土板的上下边缘处,整体动态响应下背爆面中心处开始出现不规则裂纹.在5.0 ms时刻,混凝土板迎爆面左右两边裂纹扩展至板的上下边缘,中心出现较多的裂纹,并随着损伤累积向边界方向扩展,且竖向产生了贯穿性裂纹;背爆面远离直接荷载但裂纹扩展并未停止,出现的轻微裂纹数量更多,由混凝土板中心向四周扩展至边界.在11.5 ms时刻,混凝土板中部和约束内缘处出现断裂现象,产生这种情况的原因是混凝土板上下边界约束的缺失,中心裂纹更易沿竖向扩展形成贯穿性裂纹,混凝土板朝向背爆面挤压而逐渐脱离左右边框的固定约束,整体从中间发生断裂破坏.冲击波传播到混凝土板的背爆面,形成反射拉伸波,由于混凝土的低抗拉强度特性,导致了背爆面产生更多的竖向裂纹.
图7给出了四边固定条件下混凝土板受爆炸冲击载荷作用后不同时刻的毁伤情况.在0.9 ms时刻,混凝土板迎爆面裂纹相较于两对边固定板更为均匀,在边框内缘处形成了明显的环状裂纹角;背爆面边框内缘处出现环向裂纹,中心处出现环向裂纹并开始向四周扩展.在5.0 ms时刻,混凝土板迎爆面中心出现环形裂纹,四边内缘处的裂纹也有微小扩展;背爆面开裂显著,中心处的环形裂纹沿对角线扩展,并与边缘裂纹贯通,出现多条放射状裂纹,背爆面的毁伤情况要比迎爆面更为严重,反映了反射拉伸波的作用效果.在11.5 ms时刻,混凝土板迎爆面出现较大范围破碎现象,且有向外飞溅的趋势,中间环形裂纹沿对角线扩展贯通至边缘裂纹处;背爆面形成了对角贯穿裂纹,且有碎片向外飞溅.造成与对边固定板损伤情况不同的原因是四边固定的混凝土板受力更为均匀,在大变形情况下结构动态响应得到缓冲,虽然板的破损程度更为严重,有碎片向外飞溅现象,但四边固定混凝土板并未从中间断裂,能保持更好的稳定性,且由于结构整体性较强,损伤情况分布更加对称.

图7 四边固定混凝土板迎爆面(上)与背爆面(下)的毁伤情况Fig. 7 The damages of the front surface (top) and the back surface (bottom) of the concrete slab fixed on 4 sides
3.2.2 不同爆距对混凝土板毁伤的影响
考虑两对边固定的混凝土板,其他计算条件不变,研究炸药爆距对混凝土板爆炸毁伤的影响.TNT炸药当量还是为0.15 kg,爆距分别为0.4 m,0.5 m和0.6 m.图8给出起爆11.5 ms时刻、爆距0.5 m和0.6 m情况下,混凝土板迎爆面和背爆面的毁伤情况.当爆距为0.5 m时,混凝土板迎爆面中心出现较多的贯穿裂纹,当损伤累积不足以造成结构断裂时,裂纹在中心聚集形成了较大的破碎区域,背爆面出现了多条明显的竖向裂纹,中心有裂纹聚集的趋势.当爆距为0.6 m时,混凝土板的迎爆面出现了十字状裂纹,但由于爆距不足并未使得竖向裂纹贯通,遂出现了竖向碎片,且背爆面出现微少竖向裂纹.结合图6给出的爆距为0.4 m对应的混凝土板毁伤情况可以看出,爆距增大使得作用于混凝土板的爆炸冲击荷载有所减小,裂纹扩展阻塞导致了损伤区域化累积,迎爆面更易出现破片区域,背爆面裂纹更少,混凝土板的毁伤情况也随之减弱.

(a) 0.5 m爆距(a) 0.5 m blast distance

(a) 0.1 kg炸药当量(a) For the 0.1 kg explosive equivalent
3.2.3 不同炸药当量对混凝土板毁伤的影响
考虑两对边固定的混凝土板,其他计算条件不变,研究炸药当量对混凝土板爆炸毁伤的影响.固定爆距为0.4 m,炸药当量由0.15 kg分别减少到0.1 kg、增加到0.3 kg.图9给出了0.1 kg和0.3 kg炸药当量作用下混凝土板迎爆面和背爆面的毁伤情况.0.1 kg炸药当量作用下的混凝土迎爆面出现十字状裂纹,毁伤情况不明显;背爆面中心出现横向放射状裂纹,竖向裂纹仅中间裂纹较为严重.0.3 kg炸药当量作用下的混凝土迎爆面裂纹明显,由于冲击波压力增大造成混凝土板中间发生断裂且整体呈现向下凹陷趋势,毁伤情况较明显;背爆面毁伤情况较迎爆面轻微,混凝土板断裂造成中心竖向裂纹向角隅处延展,裂纹呈现蛛网形状.
结合图6给出的炸药当量为0.15 kg的毁伤情况,可以看出,炸药当量减少使得冲击波作用减弱,混凝土板毁伤情况不显著;增加炸药当量使得混凝土板更易断裂,迎爆面下陷导致了背爆面产生放射状裂纹延伸,显著加剧了混凝土板的毁伤程度.
4 结 语
本文阐述了键型近场动力学的非连续Galerkin有限元法的基本原理,导出了计算列式,计算模拟了脆性玻璃板动态开裂分叉问题,并对爆炸冲击荷载作用下混凝土板的毁伤过程进行了计算分析,研究了板的边界条件、炸药当量和爆距等对混凝土板毁伤情况的影响,得到了一些有益的认识.
本文的研究结果表明,键型近场动力学弱形式方程对应的非连续Galerkin有限元方法,能在有限元计算框架内充分发挥近场动力学特有的非连续变形分析能力,便于施加传统边界条件和减轻近场动力学的表面效应问题,且具有较高的计算效率,能够再现爆炸冲击荷载作用下结构的复杂破裂模式和毁伤破坏过程,是能模拟结构爆炸冲击毁伤效应的方法.

