船用断路器抗摇摆性能分析研究

奚育宏，谷腾飞，于庆瑞，王 军，孙 涛，黄文辉

(1. 甘肃机电职业技术学院，甘肃 天水 741001；2. 上海大学机电工程与自动化学院，上海 200444；3. 甘肃省中高压开关工程技术研究中心，甘肃 天水 741024；4. 西安交通大学电气工程学院，陕西 西安 710049)

0 引 言

船舶真空断路器是船舶电力系统中极其重要的控制和保护设备，其工作的稳定性和可靠性对保证电力系统的稳定运行发挥着重要的作用[1]。非接触爆炸激起的海浪会引起船体产生大幅度的摇摆。摇摆运动可分为横摇、纵摇和首摇3 种运动状态[2]。船体摇摆会导致船舶真空断路器的工作姿态发生改变，从而对设备工作性能和分合闸可靠性造成不良影响。因此开展对真空断路器触头系统在摇摆载荷下的变化关系研究具有重要意义。

关于摇摆理论的研究早在18 世纪就已经开始，1861 年，Froude[3]研究了入射波作用下船体的横摇运动，提出了古典运动理论；随后Kriloff[4]对船体垂荡、纵摇运动与入射波的关系进行了理论研究，上述的研究工作共同奠定了船体摇摆运动的理论基础。尽管理论方面的研究较为成熟，而国内外对摇摆工况下船用设备动态特性的研究较少，目前的研究主要集中在有限元法和解析法方面。在有限元法方面，Chen 等[5]基于机构动态特性完成了对高压真空断路器的有限元建模和仿真分析。Zhu 等[6]对真空断路器在分合闸中由触头振动引起的电弧对触头的烧蚀现象进行了探究，在保证正常开闭的前提下提出了动静触头和支撑架之间的最优质量比和等效刚度比。Jiang 等[7]基于涡流原理设计了一种短冲程快速排斥机构，实现了对动触头闭合或分离时反向速度的动态抑制。在解析法方面，Lei 等[8]建立了速度特性、接触超调和回弹幅度之间的函数关系，通过对数值方面的校核实现了对接触超调和弹跳冲击的有效抑制。Hashemi 等[9]研究了外界磁场对真空电弧的影响，提出了一种电流过零灭弧来 提升触头开断能力的新方法。Chen 等[10]提出了鲁棒优化设计的概念，综合考虑了操动机构各个部件的公差，建立了多目标优化的非线性规划问题模型来探究 各个变量的最优参数。

综上所述可知，目前学者对真空断路器内某个系统或部件的研究较多，但对真空断路器抗摇摆方面几近空白。本文从数值计算的角度出发，建立真空断路器整机动力学模型，基于线性和非线性摇摆理论以及相关标准确定不同工况下的摇摆载荷，实现对不同摇摆工况下船舶真空断路器动态特性的研究。最后，开展真空断路器摇摆试验验证动力学模型的准确性和仿真结果的可靠性，针对真空断路器在摇摆载荷下的薄弱部位进行优化设计。

1 非线性摇摆运动模型的建立

1.1 摇摆运动的形式和特点

船舶的运动形式可以总结为3 个方向上的摇摆运动，摇摆运动可分为纵摇、横摇和首摇，相同的摇摆诱因作用在船体及船体周围的不同位置处就可能引起不同的摇摆运动，因此船体的摇摆运动非常复杂。

1.2 摇摆运动模型的构建

对于船用设备摇摆模型的建立，目前主要是基于Conolly 理论来分析和研究，但该理论只适用于线性摇摆状态（摇摆角度小于8°），对于非线性摇摆运动（摇摆角度大于8°）需引入非线性摇摆恢复力矩和摇摆阻尼力矩构建船舶非线性摇摆运动数学模型，船体摇摆运动瞬时位置受力如图1 所示。

图 1 船体摇摆运动瞬时位置受力分析Fig. 1 Force analysis of the transient position of the hull swaying motion

非线性横摇运动的摇摆恢复力矩为：

式中：C1，C3与C5均为常数。

非线性阻尼力矩为：

式中：B1， B2均为常数。

将非线性摇摆恢复力矩和非线性阻尼力矩代入得非线性摇摆运动方程为：

同理，可对其左右两侧同除Ix+∆Ix后得：

考虑到有效波倾与表面波倾的关系可得：

在等式右侧即可输出船体的摇摆角，反之根据摇摆角就可以确定船用设备的惯性载荷和力矩。经过上述推导可以得出设备摇摆运动与所受载荷之间的联系，便于确定断路器受到的输入激励。

在数值模拟时，摇摆角度和周期可以根据相关比较准备来确定，摇摆工况可以做简谐运动周期变化处理，用正弦角位移曲线模拟摇摆载荷，如下式：

式中：θ为船体在t时刻的倾斜角；A为船体的最大摇摆角度；ω0为正弦运动的角频率；ϕ0为起始时的相位角。

根据国军标GJB150.23A-2009 军用装备实验室环境试验方法第23 部分：倾斜和摇摆试验 [11]中摇摆环境规定，水面舰船的摇摆参数如表1 所示。

表 1 水面舰船摇摆参数Tab. 1 Surface ship sway parameters

将表中的摇摆参数代入公式就可实现对不同摇摆方向、摇摆周期和摇摆角度的载荷模拟。

2 船用断路器动力学模型的建立

2.1 模型建立和简化

本文研究对象为某型船用高压真空断路器。整个断路器主要由储能部分（合闸弹簧）、传动部分（连杆机构）和控制部分（操动机构）组成。分闸弹簧为左右对称布置，合闸弹簧则居中安装，起到负载均衡降低冲击的作用。

船用断路器结构复杂，若对设备按照实际结构建立动力学模型必然会导致网格划分质量较差，出现求解不收敛等情况。因此，需对其进行合理的简化，几何模型简化需遵循以下2 条基本原则：

1）简化的模型结构对计算结果影响较小；

2）简化后模型质量及网格划分质量有明显改善。

经简化处理后，设备重量由557 kg 降至530.6 kg，简化前后质量偏差为4.7%，偏差较小，符合数值计算的前处理要求，最终建立的断路器动力学模型如图2 所示。

图 2 断路器动力学模型Fig. 2 Circuit breaker dynamics model

2.2 材料属性、模型约束和边界条件

断路器的动静触头为铜件以提高灭弧室的导电和耐热性能，支撑绝缘子、玻璃布板以及绝缘拉杆为环氧树脂材料，以提高其耐热性和绝缘性。其他零部件为常见金属材料。船用断路器的数值计算主要涉及到材料密度、弹性模量和泊松比这3 个材料属性参数，主要零部件的材料属性如表2 所示，主要零部件的约束如表3 所示。

表 2 主要零部件的材料属性Tab. 2 Material properties of main components

表 3 主要部件的连接关系Tab. 3 Connection relationship of main components

整个模型共产生了256 个约束关系，主要用到固定副、旋转副和平移副，以弹簧压缩或拉伸来实现对驱动源的模拟，通过上述设置完成了断路器各零部件约束关系的建立。

断路器支撑架底部与基座通过螺栓进行连接，在静力学分析模块添加螺栓预紧力和标准地球重力后，再将角度−时间激励施加于基座底部。

根据表1 确定的摇摆参数，在横摇摇摆倾角为±45°下，分别施加3 s，5 s，7 s，9 s，11 s 和14 s 的摇摆周期；在纵摇摇摆倾角为±10°下，分别施加4 s，6 s，8 s 和10 s 的摇摆周期，以不同摇摆方向和周期作为变量研究断路器在摇摆载荷下的响应特性。

3 摇摆响应分析

在数值计算后，将不同方向和周期下的响应剧烈部位及其应力值进行汇总，为便于探究不同摇摆工况对断路器动态特性的影响，引入无量纲失效系数“η值进行描述，η的计算方式如式(7)所示。在仿真中存在12 个考核点的动态响应较大，考核点如图3 所示” 。

图 3 设备考核点示意图Fig. 3 Schematic diagram of equipment assessment points

可以看出，当失效系数η<1 时，认为结构安全；η越小，则表明断路器在该考核点的抗摇摆性能越好。

选取对断路器分合闸性能影响较大的4 个考核点，即考核点8、9、10 和11，经计算η值后生成的曲线如图4 和图5 所示。

图 4 横摇不同周期下的η 值Fig. 4 η values for different periods of transverse shaking

图 5 纵摇不同周期下的η 值Fig. 5 η values for different periods of longitudinal shaking

可知，在横摇工况下当摇摆周期为3 s，倾斜±45°时的应力响应最为严酷；在纵摇工况下周期为4 s，倾斜±10°时最为恶劣。此外还可以看出，当倾斜幅度一定时，随着摇摆周期的延长，应力响应呈现快速降低的趋势，尤其是在横摇工况下这种衰减就更为明显。这主要是因为随着周期的延长，设备的最大切向加速度和最大径向加速度将会迅速降低的缘故。横摇工况下在考核点8（支撑绝缘子）、考核点10（动触头接头）处的强度破坏最为剧烈，最大η值分别为0.991 和1.554，需对其进行强度校核；在纵摇工况下的最大η为0.89，发生在动触头接头处，存在较大的破坏风险。

在横摇周期为3 s，倾斜±45°及纵摇周期为4 s，倾斜±10°下的整体应力云图及最大应力部位如图6 和图7所示。

图 6 横摇周期为3 s，倾斜±45°下的应力响应Fig. 6 Stress response with a transverse rocking period of 3 s and a tilt of ±45°

图 7 纵摇周期为4 s，倾斜±10°下的应力响应Fig. 7 Stress response with a longitudinal rocking period of 4 s and a tilt of ±10°

从横摇和纵摇的最大应力发生部位来看，动触头接头处的应力主要集中在下端，即动触头与动触头接头的连接处，最大应力为365.26 MPa。出现此问题的主要原因是由于接头处起到向动触头传递摇摆载荷的作用，承受的负载较大，易发生应力集中。

4 断路器耐摇摆试验

为验证上述模型和仿真分析的准确性，对断路器进行了耐摇摆试验。试验设备采用基于典型Stewart 机构设计而成的六自由度摇摆台。

以横摇周期3 s，摇摆幅度±45°以及纵摇周期4 s，摇摆幅度±10°为例将仿真和由试验计算后的等效应力进行对比，对比结果如表4 和表5 所示。

表 4 横摇时等效应力试验及仿真结果Tab. 4 Equivalent force test and simulation results during transverse rocking

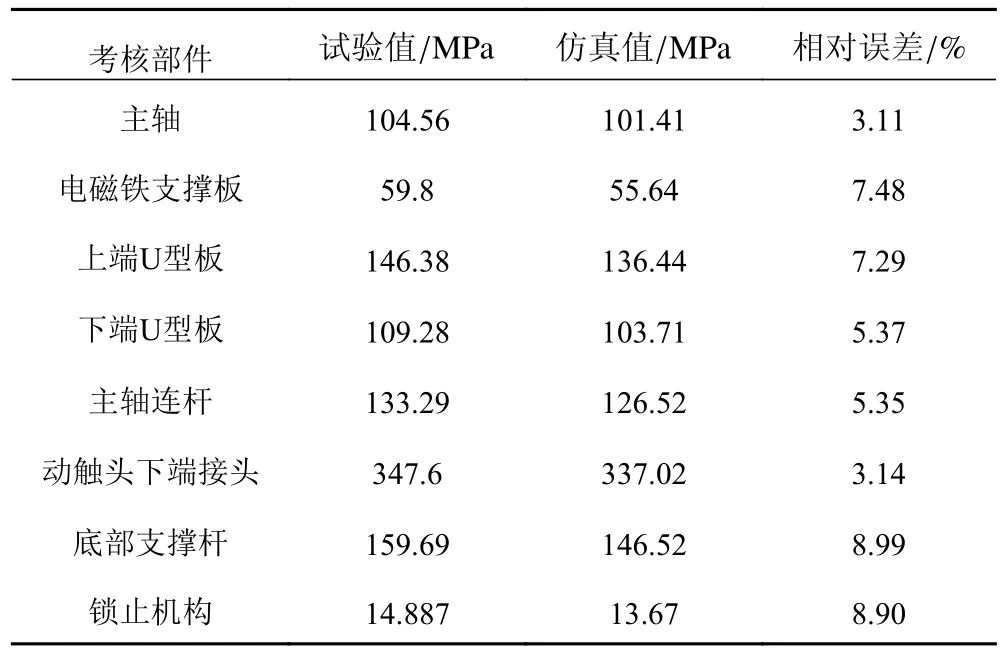
表 5 纵摇时等效应力试验及仿真结果Tab. 5 Equivalent force test and simulation results during longitudinal shaking

由表4 和表5 可见，试验与仿真的应力响应趋势基本一致，在不同摇摆工况下两者的相对误差均小于10%，验证了仿真模型的准确性。从总体上看仿真值要略小于试验值，说明在进行数值仿真和优化时需要留有较大的安全裕度以保证设备的耐摇摆性能。

5 断路器耐摇摆局部优化设计

根据整体分析的结果可知，应力分布主要集中于断路器下端接头，故在三维软件中对其采取局部倒圆角进行处理。考虑到断路器下端接头所受到的力是由U 形板自下而上传递而来的，故在本模型中将子模型局部加在区域设定在下端U 形板处。具体的加载位置如图8 所示。

图 8 载荷加载位置图Fig. 8 Loading position diagram

优化变量为接头半径R和接头圆角半径L，高度保持不变，提升接头结构的抗摇摆能力。动触头开孔直径应与接头直径相等，以便两者保持绑定接触连接关系，动触头和触头接头结构示意图如图9 和图10 所示，结构的初始参数及取值范围如表6 所示。

图 9 动触头接头示意图Fig. 9 Schematic diagram of the dynamic contact connector

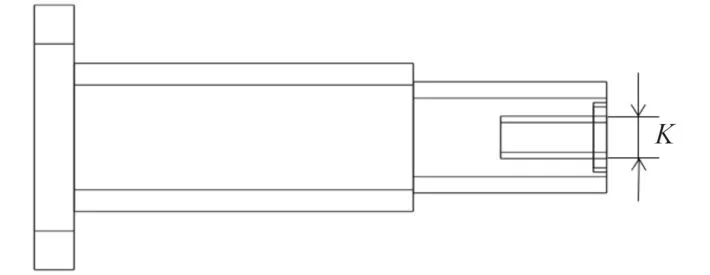
图 10 动触头结构示意图Fig. 10 Schematic diagram of the structure of the dynamic contact

表 6 动触头接头结构初始参数及取值范围Tab. 6 Initial parameters and range of values of dynamic contact joint structure

以结构的最大应力Dmax为优化目标，以优化变量的取值范围作为约束条件，约束条件为：

目标函数表示为：

对于动触头接头处，总共进行了63 次迭代，在经过32次迭代计算后目标值稳定在170 MPa 附近，迭代曲线如图11 所示。

图 11 动触头接头应力寻优迭代曲线Fig. 11 Iterative curve of dynamic contact joint stress search

在迭代的前几步，目标函数的波动十分明显，通过不断的迭代，目标函数下降的趋势越来越小，收敛过程也越发困难。由此可以看出在优化设计的开始阶段，不合理的尺寸设计在前几次迭代就会被删除，后面的迭代过程是对设计区域和尺寸的寻优逼近，因此可以在接近目标值的附近选取一个便于加工和生产的尺寸即可。经过63 次迭代，目标函数由365.26 MPa 降至166.1 MPa，最大应力值下降了54.5%，使得设备足以满足使用要求。

6 结 语

本文面向船用断路器抗摇摆性能的需求，建立船用断路器动力学模型，根据构建的非线性摇摆运动数学模型和摇摆参数，模拟断路器在摇摆工况下的动态响应，分析了断路器在不同摇摆方向、摇摆角度和摇摆周期下的应力分布，得出如下结论：

1）由断路器瞬态分析结果可知，在各种摇摆工况下，断路器的变形和应力最大位置均出现在断路器灭弧室下端接头部位。

2）通过对不同摇摆方向和周期的应力分布对比，当方向相同时摇摆周期越短则对应的应力破坏越大；当方向不同时，纵摇相较于横摇其应力分布会有所改善，在对断路器进行安装时应尽量选择纵摇以降低应力分布，提高断路器的稳定性和可靠性。

3）由应力分布可知，动触头底部接头位置出现了应力过大的情况，通过采取增设圆角的方式进行优化，经过63 次迭代计算，优化结果显示最大应力值下降了54.5%，设备强度满足使用要求。