基于VMD-Stacking混合模型的短期风速预测研究
张柯 刘海忠
摘 要: 由于风速序列高度非线性、间歇性和非平稳的特点,给预测带来了困难,从而影响了可再生能源制造。本文提出基于变分模态分解(VMD)和Stacking集成学习的短期风速混合预测方法。VMD将风速序列分解为平稳分量,以解决非平稳问题;考虑风速序列实质特征,Stacking的基学习器采用LightGBM、LSTM和全连接网络(FCN)算法。实验采用真实风速数据,VMD-Stacking混合模型的RMSE、MAE和MAPE分别为0.1772、0.1553和8.32%。与其他分解方法或不同的基学习器组合相比,VMD-Stacking充分利用时间序列特征和风速波动信息,提高了短期风速预测的准确性和稳定性。
关键词: 短期风速; 变分模式分解; LightGBM; LSTM; Stacking
中图分类号:TM614 文献标识码:A 文章编号:1006-8228(2023)05-40-05
Research on short-term wind speed prediction based on VMD-Stacking hybrid model
Zhang Ke, Liu Haizhong
(School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou, Gansu 730070, China)
Abstract: Due to the highly nonlinear, intermittent and non-stationary characteristics of wind speed series, it is difficult to predict and affects renewable energy production. A hybrid short-term wind speed prediction method based on VMD and Stacking integrated learning is proposed to improve the performance of short-term wind speed prediction. VMD decomposes the wind speed series into stationary components to solve the non-stationary problem. Considering the essential characteristics of wind speed series, LightGBM, LSTM and full connected network (FCN) algorithms are used in the basic learner of Stacking. Using real wind speed data for experiments, the RMSE, MAE and MAPE of the VMD-Stacking hybrid model are 0.1772, 0.1553 and 8.32% respectively. Compared with other decomposition methods or different basic learner combinations, VMD-Stacking makes full use of time series characteristics and wind speed fluctuation information to improve the accuracy and stability of short-term wind speed prediction.
Key words: short-term wind speed; variational mode decomposition (VMD); LightGBM; LSTM; Stacking
0 引言
能源在人們生活中一直扮演着不可替代的角色。现在许多国家都在大力发展可再生能源技术,以解决传统能源消耗的问题。许多学者已将研究重点转向风能,常用风速预测构建模型主要分为三类:统计模型、人工智能模型和混合预测模型。其中,统计模型有时间序列分析法、多元线性回归、卡尔曼滤波法等。但由于风速较强的非线性特征,其预测效果普遍较差。人工智能模型主要包括人工神经网络[1]、灰色预测[2]等,具有较强的非线性特征提取能力。然而,神经网络存在收敛速度慢[3]、对参数选择敏感、过拟合等问题,限制了其进一步发展。为了弥补其不足,混合预测模型被广泛应用。文献[4]发现,组合预测的精度高于任何单个预测,但这种高精度预测受单个模型预测误差之间的关系影响。文献[5]研究了风速序列的不同分解方法,如小波分解、经验模式分解(EMD)、变分模式分解(VMD),并比较了他们的有效性。文献[6]利用EEMD将原始风速分解为具有不同频率和一定规则的模态分量。然后将每个分量输入到遗传算法优化的BP神经网络中,每个分量的结果进行加和得到最终的预测结果。此模型有EEMD计算量大,分量不可控的问题,这往往导致函数不收敛而使风速数据的分解效果不佳。文献[7]结合了全连接网络(FCN)、长短期记忆网络(LSTM)和残差网络。通过多种模型的合理组合,取得了较好的预测结果。
为了填补上述空白,本文采用具有足够理论基础和性能优越的VMD分解方法。VMD是一种新的自适应时频分解方法,它对采样噪声具有更强的鲁棒性。此外,LSTM网络可充分利用时间序列数据之间的内在相关性,但预测精度一般[8]。LightGBM模型训练速度快、精度高,支持高效的并行训练[9],但缺乏对时间序列的整体感知能力。而对于残差变化较小的时间序列数据,FCN做为主流预测模型,精度更高。因此提出一种基于VMD-Stacking的短期风速混合预测模型。主要创新点包括:①VMD和Stacking的结合可提高风速序列预测的精度;②Stacking选择LSTM、LightGBM和FCN作为基学习器,不仅可以有效利用时间序列变化趋势,还可以充分挖掘不同波动水平下的序列信息。从这两个角度实现风速信息的全面提取,以便训练出更优越的预测模型。
1 理论介绍
1.1 变分模态分解
VMD[11]是一种新的自适应数据分解方法,根据各分解分量的中心频率和带宽,实现信号的频域分解和各分量的有效分离。VMD将信号分解,转换为变分模式,并寻找约束变分模型的最优解[12]。
对给定的信号序列y(t),VMD假设它由K个有限带宽的分量y(t)组成,通过求解约束变分问题来实现信号的分解:
[minuk,wkk=1K?tδt+jπt?uk(t)e-jwkt22s.t.k=1Kuk(t)=f] ⑴
其中,uk(t)是模态函数的输入信号,uk代表模态集合{u1,u2,…,uk},wk为第k个模态相对应的中心频率;δ(t)为狄利克雷函数,引入平衡约束参数α和拉格朗日乘法算子λ(t),以保证重构精度和约束条件的严格性,将其变为非约束优化问题:
[Luk,wk,λt=αk=1K?tδt+jπt?uk(t)e-jwkt22]
[+yt-k=1Kuk(t)22+λt,yt-k=1Kuk(t)] ⑵
利用交替方向乘子方法求解式⑵,即对uk、wk和λ(t)进行交替迭代,计算步骤见文献[13],迭代公式为:
[un+1kw=yw-i≠kuniw+0.5λn(w)1+2α(w-wnk)2]
[wn+1k=0∞wunkw2dw0∞unkw2dw]
[λn+1w=λnw+ρyw-k=1Kun+1k(w)]
其中,ρ是噪声容忍度,上式不断更新迭代,直到满足收敛精度,输出最终的uk,wk。
1.2 Stacking集成学习
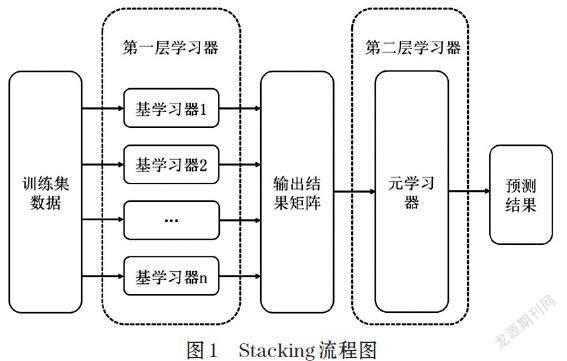
Stacking是一种分层融合模型,结构如图1所示。首先,将原始数据划分为几个子数据集后输入到第一层的每个基学习器中,其预测结果输出作为第二层元学习器的输入进行训练,由元学习器输出最终的预测结果。Stacking集成学习泛化了多个模型的结果,以提高总体预测精度[14]。
1.3 基学习算法
1.3.1 Lightgbm
LightGBM是一个基于决策树算法的GBDT推广框架[15],该算法的优点有训练速度更快、精度更高、支持并行学习等。其基本思想是将M个弱回归树线性组合成强回归树:
[FX=m=1Mfm(x)] ⑶
其中,[FX]为回归树最终的输出值;[fm(x)]为第m棵弱回归树的输出值。原理是将损失函数的负梯度作为当前决策树的残差近似值,去拟合新的决策树,即每一次迭代都保留原来的模型,再加入一个新的函数到模型中,使预测值不断逼近真实值。
1.3.2 长短期记忆神经网络(LSTM)
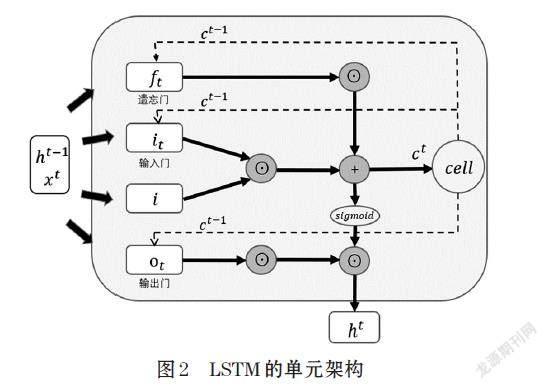
LSTM是一种深度学习算法[16],具体结构架构见图2。
每一个LSTM单元拥有一个具有记忆功能的细胞元组,其在时刻t的状态记为ct,LSTM单元通过输入门、遗忘门和输出门接收当前状态xt和上一时刻元组的状态ht-1。同时,记忆单元的状态ct-1作为内部信息将输入到各个门中。当接收输入信息后,输入门、遗忘门和输出门将进行内部运算。输入门的信号经过函数变换后,与遗忘门处理过的记忆单元状态叠加,形成新的记忆单元状态ct。最终,ct经过函数运算和输出门的控制形成LSTM单元的输出ht。各变量之间的计算公式如下:
[it=sigmoidWhi×ht-1+Wxi×xt+Wci×ct-1+bi]
[ft=sigmoidWhf×ht-1+Wxf×xt+Wcf×ct-1+bf]
[ot=sigmoidWho×ht-1+Wxo×xt+Wco×ct-1+bo]
[i=tanhWhg×ht-1+Wxg×xt+bc]
[ct=ft⊙ct-1+it⊙i]
[ht=ot⊙tanhct]
2 模型方法
2.1 VMD-Stacking模型基本信息
VMD-Stacking模型的結构如图3所示。将风速序列F分解为固有模态函数,然后将t-1时刻分解后的分量[(IMF1t-11,IMF2t-12,…,IMFnt-1)]分别输入到LightGBM和FCN以获得相应的预测结果。此外[(Ft-τ,…,Ft-2,Ft-1)]输入到LSTM,并使用每[τ]个相邻历史风速去预测t时刻的风速。最后,将三个基学习器的结果通过Stacking进行融合。
具体训练过程:
⑴ 利用MI理论选择历史风速序列的最佳预测步长([τ])。
⑵ 将数据每[τ]个分为一组,并与下一时刻的风速形成训练样本,即[(Ft-τ,…,Ft-2,Ft-1),Ft],t=τ+1,τ+2,…N,一共有N-τ组。N是训练集中的数据数,下标从1开始。
⑶ 进行归一化后,通过VMD分解以获得相应的分量{IMFt-1s},i=t-τ,t-τ+1,…,t-1,s=1,2…,n,,n是VMD的分解层数。
⑷ 分解得到的分量分别输入基学习器进行训练,{IMFt-1s}用作FCN和LightGBM的输入,(Ft-τ,…,Ft-2,Ft-1)作为LSTM的输入,分别预测t时刻的结果作为输出,然后根据结果Ft更新每个模型的参数。
⑸ 基学习器经过训练后,每个训练样本的输出形成一个三维向量[Ft`,Ft``,Ft```],作为第二层元学习器的输入,根据其输出,使用反向传播更新参数。
2.2 VMD分解
在变分模式分解过程中,当K值较小或较大时,很容易产生模态混叠或过度分解。这里采用观察中心频率的方法确定K值,从小到大取预设K值,当最后一层分量的中心频率保持相对稳定时,认为此时K值最佳。见表1,在K=8之后最后一层IMF分量的中心频率保持相对稳定,所以预设定K=8。分解结果如图4所示。
3 实验设置以及结果分析
3.1 实验数据和评价指标
实验中数据来自NOAA(美国海洋与大气管理局数据)网站获取的纽约地区2019年9月22日至27日的风速及相关的大气数据,共采集22日720个采样点,间隔为2min,其中90%数据作为训练数据,10%作为测试数据。相关模型在Python3.6环境下完成编程计算。预测评价指标采用平均相对误差eMAPE,相对均方误差eRMSE和平均绝对误差eMAE,具体如下所示:
[eMAPE=1ni=1nxj-x(i)x(i)×100%]
[eRMSE=1ni=1nxi-y(i)2]
[eMAE=1ni=1nxi-y(i)]
x(i)和y(i)分别表示i时刻的真实值和预测值;n为样本数量。
3.2 集成效果分析
由图5实验结果可知,采用Stacking集成模型的预测效果优于传统单一基础模型预测效果。表2中指标数据为重复10次预测所得到的平均值(表3、表4、表5同理),可知Stacking集成方法比单一模型的最好预测效果相对提升63.33%,有效结合了各单一算法优势,减少单一模型泛化性能不佳的风险。
3.3 分解去噪对比分析
圖6预测结果显示,使用不同的分解去噪技术对预测结果有较大影响。对比经EMD、EEMD、CEEMDAN分解处理的Stacking模型的实验结果,在此场景下,VMD对于短期风速的分解效果更佳,更为有效降低数据的复杂程度。
3.4 基学习器构建对比分析
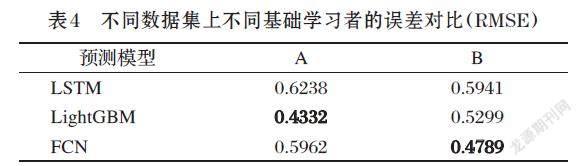
将22日至27日的4320条原始数据相邻时刻风速差设为新的序列G,G服从正态分布,称差值在区间(μ-2σ,μ+2σ)内的数据为数据A,其以外的数据称为数据B,它们分别代表风速变化幅度较小和较大的数据集合。表4为三个基学习器分别对A、B数据集的实验误差,表明对于残差变化较大的数据,LightGBM预测精度更高;对于残差变化较小的数据,FCN的预测精度更高,而LSTM对整体数据的残差的正负号预测高达89%,表明其能够一定程度上捕获时间序列变化趋势信息。综合以上分析可以得出,将三种模型进行组合后,可增强模型对长时间序列的感知力,同时充分挖掘不同波动程度下的序列信息。
由表5可知,使用不同的基学习器对预测结果有较大影响。用SVM算法来进行举例,去替换基学习器中任意一个,发现实验误差都会变大。从而验证对于Stacking基学习器选择的测试结果,并且剔除掉任何一个,评估性能都会有所下降。
4 结论
本文研究了一种基于VMD-Stacking集成学习的短期风速预测模型,并将模型应用于某风电场真实数据集,验证模型的预测精度,主要结论如下:
⑴ VMD分解可将具有强非线性、非平稳性的风速时间序列分解为相对稳定的数组IMF分量,可增强时间序列的可预报性。对比EMD、EEMD和CEEMDAN,VMD实验结果的RMSE降低了22.59%至39.97%,对于短期风速数据具有更好的分解效果。
⑵ Stacking选用的基学习器中,LSTM对风速变化正负值的预测高达89%,lightgbm在变化浮动较大的数据集上RMSE数值最小(0.4332),而FCN在浮动较小的数据集上RMSE数值最小(0.4789),三者结合具备更佳的预测效果。对比于用SVM去替换任意一个基学习器,本文模型都具有更为明显的优越效果。
⑶ VMD-Stacking的对短期风速预测误差指标RMSE、MAE、MAPE分别为0.1772、0.1553和8.32%。此模型可准确地追踪风速变化情况,在预测短期风速变化中表现出更好的预测度和稳定性。
参考文献(References):
[1] SINGH P, DWIVEDI P. Integration of new evolutionaryapproach with artificial neural network for solving short term load forecast problem[J]. Applied Energy,2018,217:537-549
[2] 焦润海,苏辰隽,林碧英,等.基于气象信息因素修正的灰色短期负荷预测模型[J].电网技术,2013,37(3):720-725
[3] 孔祥玉,郑锋,鄂志君,等.基于深度信念网络的短期负荷预测方法[J].电力系统自动化,2018,42(5):133-139
[4] BATES J M, GRANGER C W J. The combinationofforecasts[J]. Journal of the Operational Research Society,1969,20(4):451-468
[5] Qian Z, Pei Y, Zareipour H, et al. A review and discussionof decomposition-based hybrid models for wind energy forecasting applications[J]. Applied Energy,2019,235(FEB.1):939-953
[6] Wang S, Zhang N, Wu L, et al. Wind speed forecastingbased on the hybrid ensemble empirical mode decomposition and GA-BP neural network method[J]. Renewable Energy,2016,94:629-636
[7] 许言路,张建森,吉星,等.基于多模型融合神经网络的短期负荷预测[J].控制工程,2019,26(4):619-624
[8] 陆继翔,张琪培,杨志宏,等.基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化,2019,43(8):131-137
[9] 周挺,杨军,周强明,等.基于改进 LightGBM 的电力系统暂态稳定评估方法[J].电网技术,2019,43(6):1931-1940
[10] Lu X, Miao F, Xie X, et al. A new method fordisplacement prediction of 'step-like' landslides based on VMD-FOA-SVR model[J]. Environmental earth sciences,2021(80-17)
[11] 罗亦泳,姚宜斌,黄城,等.基于改进VMD的变形特征提取与分析[J].武汉大学学报·信息科学版,2020,45(4):613
[12] Hu H, Zhang J, Li T. A Comparative Study of VMD-Based Hybrid Forecasting Model for Nonstationary Daily Streamflow Time Series[J]. Complexity,2020(2):1-21
[13] Hamilton N, Ferry M. vmd: Variational Mode Decompo-sition,2017
[14] Zandi O, Zahraie B, Nasseri M, et al. Stacking machinelearning models versus a locally weighted linear model to generate high-resolution monthly precipitation over a topographically complex area[J]. Atmospheric Research,2022,272:106159
[15] Friedman J H. Stochastic gradient boosting[J].Computa-tional Statistics & Data Analysis,2002,38
[16] 張宇帆,艾芊,林琳,等.基于深度长短时记忆网络的区域级超短期负荷预测方法[J].电网技术,2019,43(6):1884-1891

