基于开源GIS 数据的广域小重叠卫星影像定位模型精化
王冬红,刘军,黄石生,张蕾,陈兴峰
(1.北京跟踪与通信技术研究所,北京 100094;2.中国科学院空天信息创新研究院,北京 100094)
0 引言
2010 年以来,随着我国高分辨率对地观测系统等重大专项的实施,国产高分遥感卫星进入密集发射期,呈现井喷式发展[1-2]。这些遥感卫星大多不具备立体成像能力,相邻影像在穿轨方向存在很小重叠,例如GF-1 卫星相邻2 台宽视场(Wide Field of Viev,WFV)相机的地面重叠仅约5%,重叠区域同名光线的交会几何条件较差[3]。
当前卫星遥感影像大多采用有理多项式模型(Rational Polynomial Camera,RPC)进行分发。为实现大区域正射影像图的快速制作,须解决广域小重叠卫星影像的区域网平差问题。2000 年以来,国内外学者对卫星影像RPC 模型的应用开展了深入研究[4-7],GRODECKI等[8-9]提出了RPC 模型系统误差的补偿方案以及区域网平差方法,随后被广泛采用。在弱交会条件下,通过引入DEM 进行RPC 模型的平面区域网平差也可取得较好定位精度[10-12]。但是,这些方法主要基于实测外业控制点开展,效率低,对于广域卫星影像将难以实施,另外对于极小重叠影像的处理考虑不足。
近年来,国际上公开的全球免费数字正射影像(Digital Orthophoto Map,DOM)、数字高程模型(Digital Elevation Model,DEM)数据源日益增多,分辨率与几何精度不断提高。基于这些开源地理信息系统(Geographic Information System,GIS)数据自动提取控制信息,可实现大区域、小重叠卫星影像RPC模型的快速精化并快速生成正射镶嵌产品,将具有广泛的应用需求和重要的实用价值。本文将以GF-1卫星的WFV 相机影像为例,通过设计无像幅约束的GPU 特征匹配以及由粗到精的RPC 模型优化方法,利用开源GIS 数据构建广域小重叠卫星影像快速几何处理的工艺流程,并对其有效性进行实验分析。
1 RPC 模型及其系统误差描述
1.1 有理多项式模型(RPC)
RPC 是国内外高分辨率遥感卫星影像分发普遍采用的成像几何模型,它将像点像素坐标(C,R)表示为以地面坐标(φ,λ,h)的有理多项式,隐藏了与传感器有关的成像参数信息,具体表达式如下[4]:
式中:p1(u,v,w)、p2(u,v,w)、p3(u,v,w)、p4(u,v,w)都是三次多项式;(u,v,w)、(c,r)为正则化的物方和像方坐标:
式中:(φ0,λ0,h0,C0,R0)为正则化平移参数;(φS,λS,hS,CS,RS)为正则化比例参数。
1.2 RPC 模型的系统误差
高分辨率卫星影像的RPC 模型是采用“地形无关”方式,通过对严格几何模型构建的控制网格点的拟合生成,而严格几何模型则须利用卫星星历、姿态数据直接建立[5]。由于卫星精密定轨、定姿系统的测量误差及其与星载相机之间的安置偏差等因素的系统性影响,高分辨率卫星影像的RPC 模型不可避免地存在系统性误差,在进行高精度几何处理时必须对其进行补偿。GRODECKI、FRASER等[8-9]提出通过在像方引入多项式来补偿RPC 模型系统误差的方法,成为RPC 模型区域网平差普遍采用的技术方案,即把由RPC 模型直接计算出的像点坐标(C,R)与实际像点坐标(S,L)之间的偏差(ΔC,ΔR),表达为(C,R)的多项式:
式中:ei、fi(i=0,1,2)为多项式系数。
通常,像方的仿射变换即可满足系统误差补偿的要求,此时RPC 模型区域网平差数学模型为[12]
1.3 广域小重叠卫星影像几何模型精化流程
由于RPC 模型系统误差的存在,大区域内的单景影像会因为较大的定位误差而无法准确接边。因此应采用区域网平差的方法,通过控制点和连接点的共同作用,提高RPC 模型的定位精度,将接边差降至像元级水平。针对广域、小重叠卫星影像,由于立体交会的几何条件差,常规的RPC 模型区域网平差方法难以收敛,须在DEM 支持下开展2D 区域网平差[11-12]。
广域卫星影像的区域网平差对控制点的需求较大,采用外业测量获取控制点的常规方式难以实施。也可通过集成星载激光测高仪,利用同步采集的激光脚点用于卫星影像的定位优化,但总体技术难度大,仅有ZY-3、GF-7 等极少数国产卫星配备有该辅载荷[13-14]。随着全球开源GIS 数据,例如Sentinel-2全球DOM、SRTM全球DEM以及Google、Bing、天地图等互联网地球/地图等公开数据集性能的不断改善,为广域卫星影像的几何处理提供了良好的物方参考信息。美国地质测量局(USGS)联合美国航空航天局(NASA)制作了全球陆地调查(Global Land Survey,GLS)系列数据集[15],最新的GLS2010 产品分辨率达15 m,RMSE 误差优于25 m[16];法国空间局(CNES)利用Sentinel-2A/B 数据制作了全球参考影像(Global Reference Image-GRI),在亚洲区域精度约20.1m[17]。全球开源DEM 有ASTER GDEM、SRTM、AW3D30 等。2014 年NASA 免费发布的SRTM全球DEMv3.0 产品,平均分辨率1″,标称绝对高程精度优于16 m LE90,相对高程精度优于10 m LE90[18];NASA ASTER GDEM 系列产品的空间分辨率为1″,2011 年发布的v2产品绝对高程精度约17mLE95[19]。这些公开数据集,为广域卫星影像几何定位精度的优化提供了全球尺度的物方参考数据。
基于RPC 模型2D 区域网平差思想,以GF-1 卫星WFV 影像为例,本文设计了一种基于开源DEM、DOM 数据的广域小重叠卫星影像RPC 模型精度快速精化的方法,以支撑大区域、多景卫星影像的快速精确镶嵌。其中的关键是小重叠卫星影像之间以及卫星影像与开源DOM 之间的快速、稳健匹配算法,本文通过改进对图像分辨率、方向具有较好适应性的尺度不变特征变换(Scale Invariant Feature Transform,SIFT)匹配算法[20],自动从参考DOM 中提取控制点信息。参考DOM 采用Landsat-8 卫星15 m 分辨率全色图像,参考DEM 采用SRTM 1″分辨率产品,整个算法流程如下:
步骤1导入WFV 影像,计算任务区的空间覆盖范围,并下载该区域Landsat-8 参考DOM 和SRTM 参考DEM。
步骤2WFV 图像与参考DOM 的分片、快速SIFT 特征提取。
步骤3控制点自动匹配与RPC 模型的第一次优化。①WFV 影像与参考DOM 的分片SIFT 特征匹配;② 采用RANSAC 算法剔除误匹配点;③采用单片空间后方交会方法,优化WFV 影像的RPC模型。
步骤4PRC 模型约束的连接点自动匹配。①依据RPC 模型以及参考DEM,两两计算WFV图像之间的重叠区域以及重叠度,并确定像对列表;② 针对每个像对,进行分片SIFT 特征匹配,获取同名点并剔除重复;③连接不同像对的匹配结果,构建各连接点在WFV 影像上的观测值列表;④在参考DEM 的支持下,采用RPC 模型的单片定位算法,计算连接点的地面坐初值[(φ,λ,h)]。
步骤5DEM 辅助RPC 模型区域网平差。①RPC 模型2D 区域网平差,求解仿射变换参数[ei,fi(i=0,1,2)]以及连接点平面坐标[(φ,λ)]改正数;② 在参考DEM 中内插连接点高程[h];③重复步骤1、步骤2,直至连接点坐标不再变化。
步骤6平差精度统计。
2 RPC 模型约束的控制点与连接点快速匹配
待平差的WFV 影像之间以及WFV 与参考DOM 之间存在投影、时相、尺度、色调等多方面的差异,因此需要可靠、高精度的影像匹配算法。近年来,特征检测算法取得了重要进展,出现了SIFT[20]、SUFR[21]、ORB[22-23]等性能良好的特征算子。本文采用David Lowe 在1999 年提出的SIFT 算法进行控制点和连接点匹配。SIFT 特征对旋转、尺度缩放、亮度变化保持不变性,独特性好,对视角变化、仿射变换、噪声也保持一定程度的稳定性[24]。
2.1 无像幅约束的SIFT 特征快速提取与匹配
经典的SIFT 算法运算量大,内存消耗高,匹配效率低。为实现连接点和控制点的快速匹配,拟采用WU 的SIFTGPU 实现[25]。针对WFV 图像和参考DOM 像幅大的问题,采用了分块提取和分块匹配的策略,使匹配不受内存和显存的限制,具体方法为:①根据内存、显存容量,选择合适的滑动窗口大小,将WFV 和参考DOM 图像分为若干瓦片,每个瓦片分别导入SIFTGPU 提取SIFT 特征描述子;② 分块存储各瓦片的SIFT 特征描述子;③针对主影像的每个瓦片,依据RPC 模型和参考DEM 计算其四角点在辅影像上的位置,确定在辅影像上的瓦片组,然后在主影像瓦片与辅影像瓦片组的SIFT描述子之间采用SIFTGPU 进行特征匹配;④ 遍历主影像各个瓦片,重复开展上一步的匹配处理,汇总得到整个影像的匹配结果。
SIFTGPU 在处理较大幅面的图像时,受GPU存储容量的局限通常会降分辨率处理。本文设计的上述匹配方法,使SIFT 特征的提取与匹配过程不受GPU 存储能力的限制,适合任意大小的遥感图像。由于它是在图像的原始分辨率而不是缩小片上开展运算,保证了SIFT 特征提取与匹配的精度。
2.2 控制点匹配与RPC 模型的第一次精化
采用上述SIFT 分块匹配算法,可在WFV 影像与参考DOM 之间匹配出大量同名点,得到控制点平面坐标(φ,λ),然后在参考DEM 中内插出高程h,即可得到每个WFV 影像完整的控制点坐标。此时匹配得到的控制点,存在大量的误匹配,需要进行初始匹配点的自动粗差剔除,拟采用近年来兴起的随机抽样一致性RANSAC 算法。RANSAC 算法在对可能包含被粗差(outliers)污染的数据进行模型参数估计时,具有很强的鲁棒性,可以容忍样本中存在50%左右的粗差[26]。
利用剔除粗差后的控制点,采用单片空间后方交会的方法,逐个WFV 影像求解式(4)的仿射变换参数ei、fi(i=0,1,2),对RPC 模型的系统误差进行补偿,实现对RPC 模型进行第一次优化,将其定位精度提高到像元级水平,从而为连接点匹配提供更高精度的几何模型约束。
2.3 RPC 模型约束的连接点快速匹配
基于优化后的RPC 模型,采用SIFT 分块匹配算法,可在相邻WFV 影像之间匹配出大量连接点。由于此时的RPC 模型已具有较高的精度,匹配与粗差剔除的过程将比较简单,其中的关键是RPC 模型单片定位算法,亦即如何利用像坐标(S,L)和参考DEM,计算相应的地面坐标(φ,λ,h)。
RPC 模型单片定位计算的原理如图1 所示。先给定初始高程h0,然后将其代入RPC 模型,计算出地面点P0(φ0,λ0);利用(φ0,λ0)在DEM 中内插出高程h1;利用h1和RPC 模型计算出新的地面点P1(φ1,λ1)。上述过程迭代进行,直至地面点坐标不再变化时停止。采用上述算法,相邻WFV 影像之间的连接点匹配将具有较高的成功率和较好的匹配效率。

图1 RPC 模型的单片定位原理Fig.1 Principle of single image positioning based on the RPC model
3 DEM 辅助的小重叠卫星影像区域网平差
常规的RPC 模型区域网平差算法,要求立体影像之间具有较好的交会条件,仅适用于IKONOS、GeoEye-1、ZY-3 等测绘卫星立体影像。然而对于类似于GF-1 等地球资源卫星获取的具有少量重叠影像对,同名光线交会条件很弱,采用传统的RPC区域网平差算法极易造成高程求解的异常。为此,需要引入DEM 对平差过程进行约束,采用2D 区域网平差算法对RPC 模型进行优化,以适用于GF-1大区域、多景影像的联合平差处理。
RPC 模型的2D 区域网平差,数学模型仍为式(4)所表示的扩展RPC 模型,只是在平差过程中仅求解连接点平面坐标的改正数。其基本误差方程为
在区域网平差的每一次迭代中,先采用2D 区域网平差求解出平面坐标(φ,λ),在DEM 中内插出各连接点对应的高程h,然后进行下一次的迭代计算,直至参数ei、fi不再改变。
4 实验与分析
4.1 实验数据
本文采用2014 年3 月17 日GF-1 卫星获取的我国中部地区的宽幅影像对文中的算法进行验证。实验影像共包含24 标准景WFV 影像,由4 台WFV相机在一次轨道飞行中获取,地面覆盖总范围近100 万km2,分布如图2 所示。其中,有4 景影像云量超过20%,测区左上角2 景影像云量更是超过45%,这将对控制点和连接点匹配造成不利影响。下载该区域Landsat-8 参考DOM 共计32 景,并同时下载该区域30″格网间距的SRTM 参考DEM 数据。

图2 GF-1WFV 影像与匹配的控制点、连接点分布Fig.2 Distribution of GF-1 WFV images and matched control and tie points
4.2 控制点匹配与RPC 定位误差分析
按照上文的控制点匹配思路,先逐个将参考DOM 与WFV 影像进行SIFT 特征匹配,然后采用RANSAC 算法进行粗差剔除。经统计,在24 景WFV 影像中,最多成功匹配3 862 个地面特征点,最少也匹配成功45 个地面特征点,如图2 所示(经抽稀处理)。由于云层遮挡的影响,实验区北部的WFV影像上成功匹配的地面特征点相对而言明显偏少。
将每景WFV 影像上匹配出的特征点,利用参考DOM 的定位参数计算出相应的平面坐标,然后在SRTM 参考DEM 中内插出高程,得到该特征点的三维空间坐标。利用WFV 影像附带的RPC 模型,将各特征点投影到像方,计算出像点坐标(C,R),将其与该特征点匹配出的WFV 像点坐标(S,L)比较,得到RPC 模型的像方定位误差(Root Mean Square Error,RMSE),并按WFV 相机的编号统计,见表1。

表1 WFV 影像RPC 模型的像方定位误差(RMSE)Tab.1 Positioning RMSE of the RPC model for WFV images
从表1 可以看出,本次实验所采用的WFV 影像定位精度较差,在列方向尤其明显,都有近60 像元的系统偏差。4 台WFV 相机的定位精度也有明显差异,WFV4 的精度要明显优于其他3 台相机,WFV1 的定位精度最差。在不考虑参考DOM、DEM 数据误差的情况下,按照16 m 的像元分辨率计算,24 景WFV 影像原始RPC 模型的平均定位精度约为1 km。
6 景WFV1 影像RPC 模型在列、行方向的定位残差沿CCD 线阵的分布如图3 所示。从图中可以看出,L1 级WFV 影像的定位误差存在明显的系统性。从RPC 模型的生成原理可知,这主要是由于卫星的姿态数据误差和相机内参数检校误差等共同引起的,极可能是前期在轨几何标定的参数发生了一定变化,需要重新进行几何标定。
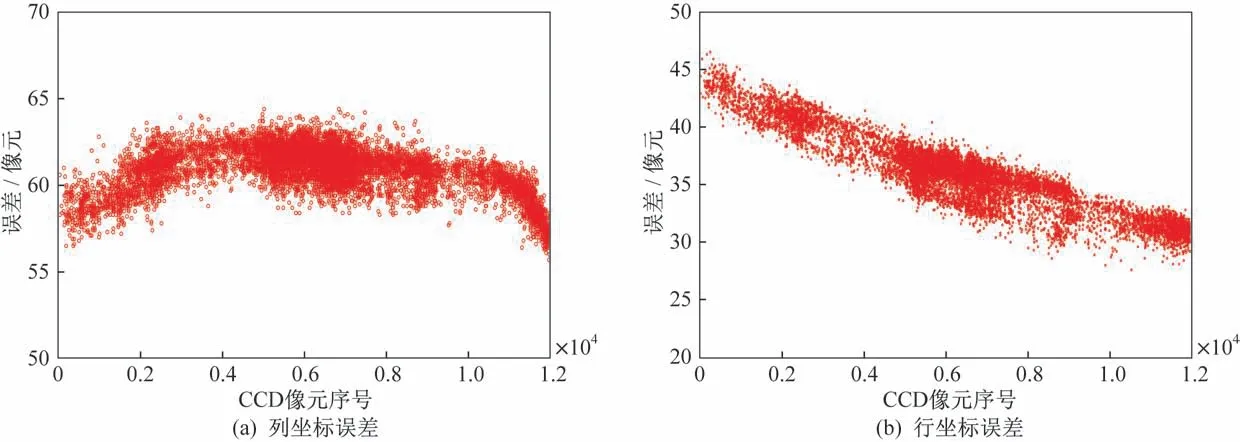
图3 WFV1 相机的像方定位残差分布Fig.3 Positioning residual distribution of WFV1 images
4.3 区域网平差后的检查点精度分析
将WFV 影像与参考DOM 匹配出的地面特征点,按照1∶4 的比例随机抽取部分点作为地面控制进行2D 区域网平差,其余点用于平差精度的检核。区域网平差完成后,将检查点地面坐标代入优化后的RPC 模型,计算出像点坐标(C,R),将其与该特征点匹配出的WFV 像点坐标(S,L)比较,得到优化后RPC 模型的像方定位误差,并按WFV 相机的编号统计,如图4 所示。

图4 各影像检查点的像方反投影RMS 误差Fig.4 Back projection error(RMS)of the check points on each image
从图4 的结果可以看出,经过区域网平差之后,RPC 模型的定位精度得到显著提高。经统计,在参与平差的24 景WFV 图像上,检查点反投影到像方后列坐标的RMS 误差平均为0.6 像元,行坐标RMS误差平均为0.5 像元。与表1 所示的平差前的定位精度相比有了显著提高,在行、列方向均达到子像元级。上述结果表明本文设计的方法是有效的,可为大区域小重叠卫星影像的正射镶嵌提供理想的技术手段。
4.4 平差后正射校正的接边误差分析
利用区域网平差精化后的RPC 模型对参与平差的WFV 影像进行正射校正,不同景WFV 图像生成的DOM 影像之间仍会存在接边误差,该误差可通过连接点来进行分析。基于连接点的像坐标,利用精化的RPC 模型,在参考DEM 的支持下采用单片定位方法计算出地面坐标,然后通过比较连接点在左右影像上的地面坐标之差即为DOM 接边误差。将接边误差按照WFV 影像的分辨率换算为像元,并统计为分布直方图,如图5 所示。

图5 连接点地面坐标差分布直方图Fig.5 Histogram of the ground coordinate differences for tie points
从图5 可知,经过区域网平差后RPC 模型的精度显著提高,生成的DOM 接边误差较小,优于0.6像元的连接点占总数的92.5%。经统计,平面方向接边误差的RMS 误差约0.4 像元,可较好保证DOM 的镶嵌精度。
5 结束语
由于卫星星历与姿态数据误差的影响,高分辨率卫星遥感影像RPC 模型的定位误差主要呈现系统性,在进行大区域正射影像图制作时需要进行区域网平差处理,但对于非立体测绘卫星获取的小重叠像对,由于极弱的立体交会条件常规的三维区域网平差方法难以获得理想结果。本文设计了一种基于开源DOM、DEM 数据的广域,小重叠度卫星影像RPC 模型精度优化的方法,并利用GF-1 WFV影像进行了验证。结果表明:RPC 模型经过两次优化之后,可以达到像元级的定位精度,为大区域卫星正射影像图制作提供了另一种技术途径。

