插电混动汽车故障率研究
林 甄 陈奕健 谢金冶
(三亚学院,海南 三亚 572022)
0 引言
由于发展可靠性能够很好地减少产品带来的影响[1],因此插电混动汽车的可靠性研究十分重要,随着社会的飞速发展,人们的生活水平越来越好,消费需求更加旺盛,对产品的要求也越来越高。在国家大力提倡低碳出行、环保主义以及节能减排的背景下,插电混动汽车的到来无疑是雪中送炭[2]。
提高插电混动汽车的可靠性可以有效降低产品在整个寿命期间的费用。按照前期提出设想、规划、设计到开始试验、打造流程、试生产、运输、储存、使用、维修以及报废过程中产生的费用,都可以通过可靠性的研究来降低[3]。
1 故障率研究内容
该文针对插电混动车辆在行驶过程中出现的问题进行研究分析,以威布尔理论分布为基础,通过线性计算获得完整的函数图表,研究其损耗出现的原因以及如何减少劳损的方法等。
该文从安全性的基本理论出发进行概括性的阐述,进行整车的插电混合动车安全性的数据采集,包括线下走访、网页信息采集、对整理好的资料进行分析处理等。利用函数特性对工程可靠性理论进行分析,最终确定在实际工程中的适用范围。
其中理论分布的计算和验算以线上、线下采集的信息为准进行分组计算、查证,利用微软旗下的软件表格进行函数曲线图表的绘制,得出整体的故障概率走向,研究其分布规律并应用到实际中,最终对其可靠度进行计算验证。在此过程中可以利用现有的可靠性模型进行比对,建立一组具有插电混动汽车故障运行里程分布动态模型,其中包括损耗间隔里程概率密度模型、可靠度模型和消耗概率模型,并进行初始耗损期、特征亏耗期和损耗期的分析等[4-6]。
2 原始故障数据的获取和分析
该研究主要采用线下采集信息法、线上收集法、大数据挖掘等方式收集研究资料。利用文献分析梳理当前插电混动汽车大数据的研究现状。1)线下调查信息收集法:走访各个4S 店、汽车维修厂等。收集研究过程中所需要的新能源汽车的故障信息,进行统计、整理,得到数据。2)线上收集:通过互联网浏览、搜寻插电混动汽车论坛、问卷调查、政府政策网页与网站,查询相关电子数字资料,从中获得最新国外新能源汽车与大数据的动态信息。3)大数据挖掘:首先获取经授权采集的汽车网站数据,通过URL 管理模块对计划爬取或已经爬取的URL 进行管理,然后利用网页下载模块对URL 管理模块确定的URL 实施访问下载,将下载的内容清洗数据并保存。
经过上述数据整理后,根据大数据分析系统获得结果信息。具体数据见表1。
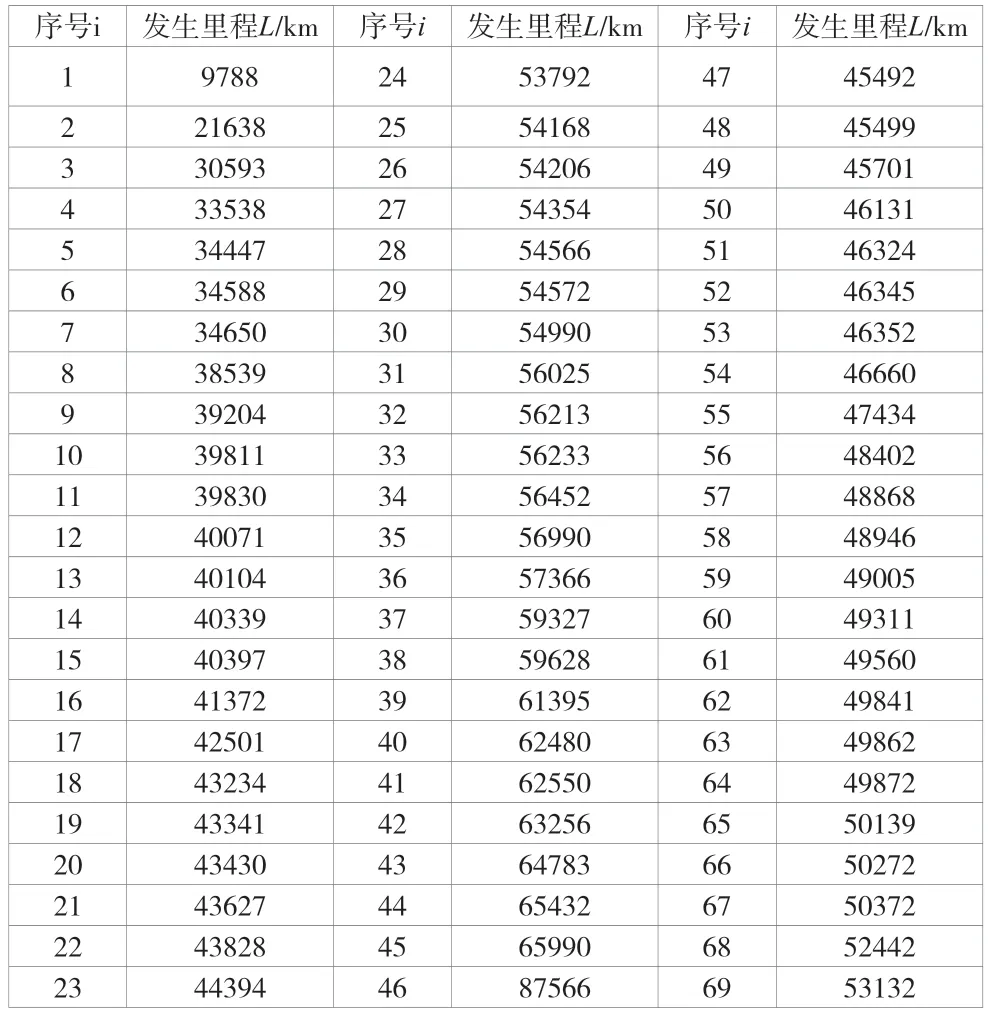
表1 故障数据表
从表1 可看出,行驶里程在3~4 万km 时发生的故障最多;在5~6 万km 后,车辆基本达到稳定状态,没有出现高频率故障。可以得出行驶里程5~6 万km 是车辆特征无故障工作里程,行驶里程3~6 万km 是车辆中位无故障工作里程。
3 插电混动汽车的故障发展规律模型
3.1 理论分布参数估计
基于前面收集到的汽车信息,可以对插电混动汽车的故障行驶里程进行近似等于威布尔分布,即服从两参数变量威布尔理论分布,通过观察分布规律建立一组参数模型。
观察规律演变时,应该先计算各个函数的分布值,通过计算结果和函数曲线图像的对比研究其规律频谱图的走向。
函数分布值有赋值法、特值法的计算方法以及整除特性的思想。但在理论分布研究中最常采用回归法。线性回归分析是一个专门处理变量的统计关系问题的数理统计技术,是用来确定2 种及2 种以上分布函数关系的一种统计方法。将涉及的函数先进行线性化处理,两边连续取对数之后展开分析,计算得出之前假设的模型变量,其中公式定义来自于艾艺红的概率论与数理统计[7]。
进行线性回归后的相关计算如下所示。
三参数威布尔分布W(b,θ,m)的故障概率密度函数f(L)、分布函数F(L)与故障率λ(L)分别如公式(1)~公式(3)所示。
式中:b为形状参数;θ为特征值,也称为尺度参数。
3.1.1 线性回归化
由可靠度R(L)与不可靠度F(L)的关系式R(L)+F(L)=1 可得公式(4)。
对公式(4)进行线性回归化,两边连续取2 次对数可得公式(5)。
通过对原函数的线性回归化,将原函数的参数估计转化为对线性函数的参数b、A的估计。
3.1.2 参数估计
通过数列(xi,yi)(i=1,2,3,...,n,n=69),利用最小二乘法,运用Excel 软件对函数关系式进行线性拟合,即可得出参数b、A的值。由公式(3)~公式(7)和表1 的各故障里程点L值可得出xi和yi,其中i=1,2,3,…,53。然后可以得出多组数列(xi,yi),拟合曲线图如图1 所示。
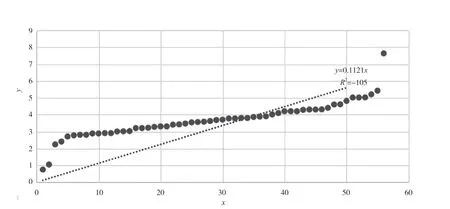
图1 拟合曲线图
拟合所得参数,b=0.769,A=2.7528,代入公式可得Θ=5.349。经理论分布假设检验后,可以判定故障发生里程数据服从威布尔分布的整体。
3.2 理论分布的假设检验
在3.1 节中,假设插电混动汽车故障数据的分布规律属两参数威布尔分布,然后对已知数据进行线性拟合,最终求出分布函数。
为了检验数据点符合拟合直线的程度,该文定义了拟合优度,如公式(9)~公式(11)所示。
式中:i=1,2,3,...,n,n=69;x、y与上节定义相同。
利用tn-2,1-a/2来确定临界拟合优度rc2,如公式(11)所示。
式中:a为1 分布的显著水平。
确定临界拟合优度rc2与拟合优度r2之后,通过验证是否满足不等式r2>rc2来判断y与x之间是否存在线性关系y=bx+A。
在新课程改革之前,传统的教学模式以老师为中心,灌输式地向学生传授书本知识,导致学生在课堂上昏昏欲睡,课堂效率低下,这是因为传统的教学观念完全忽视了学生才是教学的主体,没有考虑到学生接受知识的能力,因此,提高初中历史课堂教学的效率,教师必须摆脱传统教学观念,更新历史课堂的教学模式,为高效课堂的构建打下良好的基础,历史教师还应该具备现代化的教学理念,在高校课堂的教学中,以学生为中心,营造轻松的学习氛围,激发学生对历史的兴趣,提升学生自主思考的能力,帮助学生养成良好的思维习惯,为学生之后的学习打下坚实的基础。
计算得出=35,=3.6626,r2=0.91>0.9。
如果满足检验要求,则可以判断y与x之间存在的线性关系可信,可以判定故障发生里程数据服从威布尔分布的整体。
3.3 插电混动汽车故障分布规律的趋势研究
故障分布规律的趋势研究主要是以可信的理论分布得出相关的特征函数,如故障累计概率F(L)(既分布函数)、概率密度函数f(L)、失效率函数λ(L),绘制其总数居里程数的函数图。
由3.2 节得出可靠性数据服从于二参数威布尔分布W(0.0769,5.349),并检验其可信。
3.3.1 故障分布趋势分析
已知分布的参数,可得可靠度函数R(L)与故障分布函数F(L),如公式(12)、公式(13)所示。
故障概率密度函数f(L),如公式(15)所示。
3.3.3 故障率趋势分析
根据理论模型,可得故障率函数λ(L),如公式(15)所示。
3.4 故障发展规律寿命周期分析
该文的可靠性特征量估计值为以下各项数值。1)特征寿命L0.37。根据特征寿命的定义和威布尔分布参数的意义,θ即为特征寿命,单位为万km,根据计算可得L0.37=53490km。2)中位寿命L0.5。由可靠度关系式可知,里程点LR处的可靠度变换后可得。将R=0.5 时的里程值代入可得L0.5=9106km。3)可靠寿命L0.9=268km。4)平均故障间隔里程Lm。在该研究中,理论分布威布尔分布的概率密度函数f(L)为连续的+∝函数,则其中。当b=0.0769 时,由Γ 表可查出。代入参数,可得平均故障间隔里程Lm=44985km。
根据上文计算可靠性特征量估计值,通过这些数值可以将插电混动汽车的可靠性在量度方面进行评价,具体数据见表2。

表2 插电混动汽车可靠性特征量估计值
4 结论
该文首先对插电混动汽车现今所处地位以及未来的发展方向进行了概述,介绍了目前传统燃油车、新能源汽车和插电混动汽车三者的发展情况,结合现在环境问题以及能源危机的大背景讨论发展插电混动汽车的重要性以及提高汽车可靠性的意义。
其次,分析可靠性工作中数据处理的关键作用。按照以往的工作经验,可靠性数据的分布规律通常都可以用某些科学方法进行近似分析,而运用上述科学分布法可以针对实际工作问题进行可行性分析,论述了可信度研究工作中最常见的4 个科学方法:指数分布、正态分布、对数正态分布和威布尔分布(包括三参量与二参数)。利用威布尔二参数检验插电混动车辆故障发展变化规律,并对线性参量的回归化、模型拟合优度和临界模型拟合优度对特征量数据和所使用的样本数据的处理,得出汽车故障演变规律与里程L服从于威布尔分布。
分析收集到的69 条数据,最终得出插电混动汽车故障发生情况如图2 所示。可以看出与发动机有关的故障发生概率最大,总共出现18 次,其次就是与电机有关的。插电混汽车的故障规律主要体现在以上2 点。
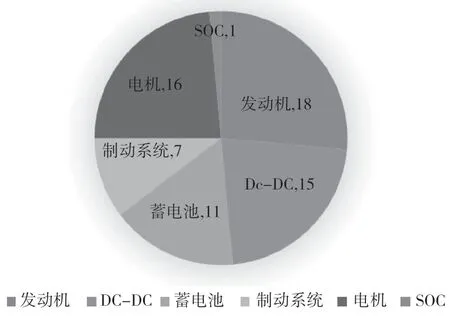
图3 故障规律分布图

