基于几何非线性动力组合地基梁模型的漏粪地板自振特性

李百丰 张焱辉 曹琼琼,2 罗 双,3 梁宗敏 蒋秀根*

(1.中国农业大学 水利与土木工程学院,北京 100083;2.铁总服务有限公司,北京 100844;3.中国农业科学院 基本建设局,北京 100081)

设施养殖由于其养殖工艺标准,生长环境可控,设施设备完备,满足健康、绿色、安全的要求,是现代养殖业的主流生产方式[1]。养殖设施的结构,需要满足对环境耐久性和对装备适用性的要求。以应用最为广泛的猪舍为例,为了满足清洁生产的需求,普遍采用条形漏粪孔地板下、配备自动清刮设备的粪沟[2]。除了满足常规荷载下地板的承载力要求外,漏粪地板还应满足由于振动产生的2方面功能需求：一是满足动物福利要求,对地板振动进行控制,不致由于地板的强烈振动,而引起猪的强烈应激;二是满足地板耐久性要求,不致由于猪粪便的强腐蚀性和振动产生的裂缝损伤积累2个因素的效应叠加,而引起的使用年限明显降低。与一般建筑物楼板振动舒适性设计不同的是,漏粪地板简单支承于粪沟两侧的地面上,可视为由两端的弹性地基梁和中段的普通梁组成的连续梁,呈现出典型的组合地基梁特征,其振动分析必须考虑组合弹性地基梁的受力特征。

弹性地基梁是指支承在连续弹性地基上的梁。在结构分析时应该将其看作是结构-地基之间相互作用的模型进行力学分析,即应考虑弹性地基梁与地基之间协调变形。由于连续弹性地基的存在,弹性地基梁具备了受力及变形2方面特征：由连续分布支承提供分布力的作用;由弹性支承同时提供几何约束和梁端自然边界条件[3-4]。在实际工程中,房屋建筑工程中基础梁板、护坡,交通工程中的公路面板和机场跑道等结构具有典型的弹性地基梁受力特征,设施农业建筑中的地板也应按照弹性地基梁模型进行分析。

当遇到动力作用时,结构在变形过程中产生的惯性力,除了引起附加的内力和变形,影响结构的安全性和适用性外,产生的振动还会引起结构舒适性以及混凝土的裂缝损伤积累导致的耐久性下降[5]。因此对于弹性地基梁分析,除了要考虑基本的静力分析外,还应考虑结构的动力响应分析。

国内外已有研究在弹性地基梁的静动力响应方面取得了一系列成果,包括弹性地基梁静力内力及变形的有限差分求解方法[6];压剪地基上Timoshenko梁的动力分析问题求解方案[7];基于微分变换法的自振频率初参数求解办法[8];不同边界条件下的弹性地基梁自振频率解析解[9];基于最小势能原理的弹性地基梁静力求解办法[10-11];移动动力荷载下黏弹性地基平动Euler梁的动力响应分析方法[12-13]。但目前关于弹性地基梁分析模型问题的研究相对较少。基于分布质量模型的Winkler弹性地基Euler梁求解办法,对于地基和梁的剪切效应并未考虑[14]。Mously等[15]对Pasternak地基上的平转动Timoshenko梁进行研究,给出了基本固有频率近似显式计算模型,但研究仅基于近似位移方程而不具有普遍性。黏弹性Pasternak地基平动Timoshenko梁的自振特性分析模型未考虑地基梁的转动特性[16]。王亚升等[17]采用最小势能原理方法,获得了受轴向压力双参数弹性地基平动Euler梁自振问题的求解办法,但仅考虑了单参数弹性地基,未能构建全参数的弹性地基梁分析模型。围绕楼板振动对人以及仪器设备的舒适度影响已展开了许多研究,如对各国建筑结构设计规范中楼面舒适度设计要求的汇总和对比,以及以频率和峰值加速度作为控制参数的建议指标限值[18-19];基于人体动力试验的人体舒适度评价方法[20];楼板自振频率和加速度的简便求解方法[21];通过蒙特卡洛随机模拟过程给出的人行荷载下复杂结构楼板振动舒适度评价标准[22]。

本研究拟对猪舍中漏粪地板的自振特性进行分析,考虑地基的压缩和剪切刚度、梁的弯曲和剪切变形、运动的平动和转动惯性力,以期建立几何非线性双参数弹性地基梁运动方程,给出组合地基梁自振周期求解模型。

1 基本模型与理论

1.1 模型及假定

对于弹性地基梁,按照右手螺旋准则建立坐标系,以梁的左端截面形心为原点O,梁轴线为x轴,向右为正;y轴垂直于梁轴线,向下为正;z轴垂直于xOy平面,向内为正。对弹性地基梁进行受力分析见图1。

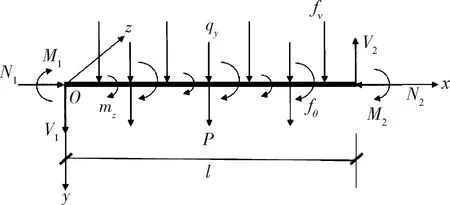
V1,V2分别为左端截面和右端截面的剪力;M1,M2分别为左端截面和右端截面的弯矩;N1,N2分别为左端截面和右端截面的轴力;l为弹性地基梁长度。V1 and V2 are shear force of left section and right section.M1 and M2 are bending moment of left section and right section.N1 and N2 are axial force of left section and right section.l is elastic foundation beam length.图1 弹性地基梁坐标系及受力示意图Fig.1 Coordinate system and force diagram of elastic foundation beam

弹性地基梁所受外力包括,轴力N0、分布线荷载qy、分布弯矩荷载mz、截面上的地基反力P、惯性力fv、惯性力矩fθ。规定荷载方向与坐标轴方向一致为正,轴力以压力为正。内力包括弯矩M和剪力V。规定当截面法线方向与坐标x轴正向一致时,内力与坐标轴方向一致为正;当截面法线与坐标x轴正向相反时,内力与坐标轴方向相反为正。

弹性地基梁位移包括,挠度v、轴线转角φ、截面转角θ、截面剪切角γ、截面曲率κ。规定位移与坐标轴正向一致为正。

本研究基于以下基本假定：等直梁模型,梁的各个截面相等且始终保持为平面;Timoshenko梁模型,考虑剪切作用的影响,轴线转角等于截面转角与截面剪切角之和;全惯性模型,考虑梁的横向振动和转动惯性力;大挠度模型,考虑轴力在挠度上产生的二阶弯矩;线弹性模型,梁的刚度保持不变,内力和位移的关系服从胡克定律;压剪地基模型,梁与地基无分离,结构-地基之间竖向位移一致。

1.2 基本方程

弹性地基梁位移控制方程是在平衡方程、几何方程、物理方程和地基模型的基础上建立的。本研究以弹性地基梁微段隔离体为研究对象建立基本方程。

1.2.1平衡方程

分别建立剪力平衡方程和弯矩平衡方程：

(1)

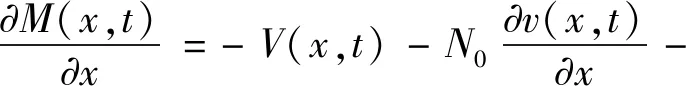
(2)

式中：b为弹性地基梁的宽,m;m为弹性地基梁的线密度,kg/m;ρ为材料体积密度,kg/m3;I为弹性地基梁对z轴的截面惯性矩,m4。

1.2.2几何方程

弹性地基梁的几何方程为[23]：

dv=tanφdx=φdx

(3)

(4)

(5)

1.2.3物理方程

弹性地基梁的物理方程为[24]：

M=EI·κ

(6)

(7)

式中：E为梁的弹性模量,GPa;G为梁的剪切模量,GPa;A为梁的截面面积,m2;μ为梁的截面剪应力分布不均匀系数。

1.2.4地基模型

压剪地基模型单位面积上地基反力的表达式为[3]：

(8)

式中：k为地基压缩刚度,N/mm3;Gp为地基剪切刚度,MPa。

1.3 控制方程

采用分离变量法,令：

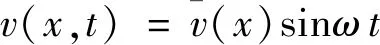
(9)

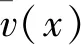
综合基本方程(1),(2),…,(8),结合式(9),得到弹性地基梁挠度控制方程为：

(10)

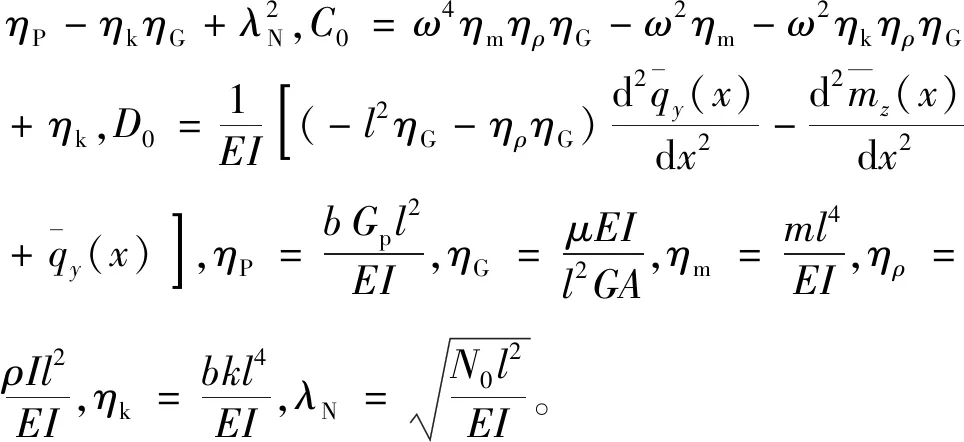
进一步,得到截面转角及截面剪切角控制方程为：

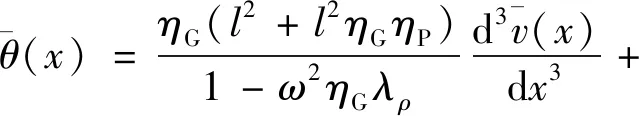
(11)

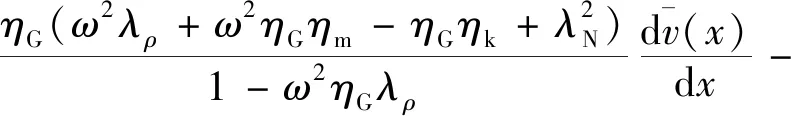
(12)

1.4 位移及内力

1.4.1挠度

求解控制方程(10),得到弹性地基梁挠度四阶齐次微分方程通解的一般形式为：

(13)

式中：c1,c2,…,c4为位移系数;r1,r2,…,r4为方程的特征根。

挠度通解(13)的向量格式为：

(14)

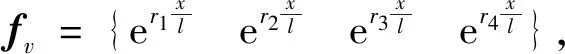
基函数导数向量表达式为：

f′v=fvZv

(15)

式中：Zv为挠度基函数向量对应的导数转换矩阵。不同工况下挠度基函数向量表达式见表1。

表1 不同工况下挠度基函数向量表达式Table 1 Deflection basis function vector expressions under different working conditions

导数转换矩阵可由基函数向量求导得到。例如,对于工况5导数转换矩阵为：

(16)

对于工况7导数转换矩阵为：

(17)

1.4.2变形

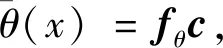
1.4.3内力

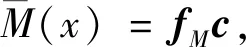
2 组合地基梁自振分析

2.1 结构模型及边界条件

典型的组合地基梁为由两端搭支在弹性地基上的弹性地基梁与中间悬空的普通梁组成的三段连续梁(图2)。结构参数为：支承长度lⅠ=lⅢ=250 mm;沟宽lⅡ=3 000 mm;地基压缩刚度k=100 N/mm3;地基剪切刚度GP=40 MPa。组合地基梁的边界条件见表2。

Ⅰ、Ⅱ、Ⅲ为杆件编号;1,2,…,4为节点编号。Ⅰ、Ⅱ、Ⅲ are lever number,1,2,…,4 are node number.图2 组合地基梁示意图Fig.2 Diagram of combined foundation beam

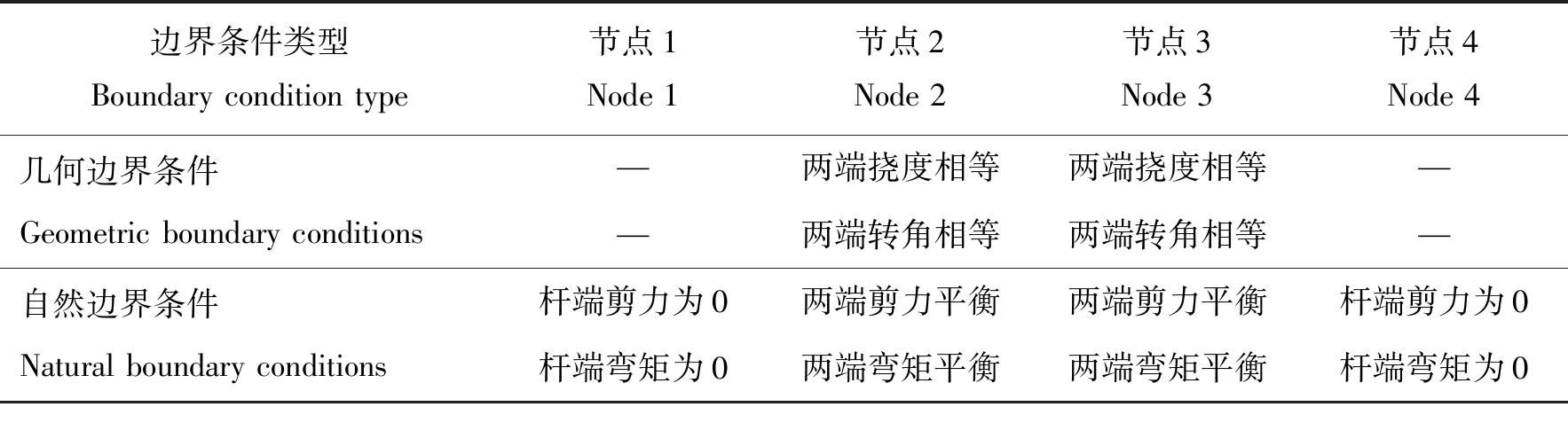
表2 组合地基梁边界条件Table 2 Combined foundation beam boundary conditions

2.2 组合地基梁自振方程

依据组合地基梁边界条件,代入位移及内力表达式建立自振方程：

Acoefc=0

(18)

式中：Acoef为系数矩阵,表达式为：

(19)

式中,c为位移系数向量,c={c1c2…c12}T。

2.3 自振周期及振型分析

Acoef中的元素均是与自振频率ω相关的表达式。对于齐次线性方程组,振动时有非零解,须满足系数矩阵行列式等于0,即得到自振频率的特征方程：

|Acoef|=0

(20)

采用数值计算方法,求解方程(20)得到组合地基梁的自振频率。将自振频率代入周期计算公式：

(21)

计算出组合地基梁的自振周期。将自振频率回带自振方程(18),求得对应的位移系数向量。结合挠度表达式(14)得到各模态下弹性地基梁振型曲线。

3 算例与分析

3.1 组合地基梁自振特征

为研究组合地基梁的自振特征,以典型漏粪地板为分析对象,采用压剪地基平转动Timoshenko梁模型对其进行自振分析。结构参数为：截面尺寸100 mm×100 mm、支承长度lⅠ=lⅢ=250 mm、沟宽lⅡ=3 000 mm、地基压缩刚度k=100 N/mm3、地基剪切刚度GP=40 MPa、材料的弹性模量E=32.5 GPa、剪切模量G=11.4 GPa、密度ρ=2 400 kg/m3、截面剪应力分布不均匀系数μ=1.2。

采用本研究模型,计算得到组合地基梁前5个模态的振型曲线见图3。结果表明：1)采用本研究模型可以有效得到组合地基梁的自振周期和振型曲线;2)与普通梁相比,组合地基梁的振型出现了非单调波形增加的现象。

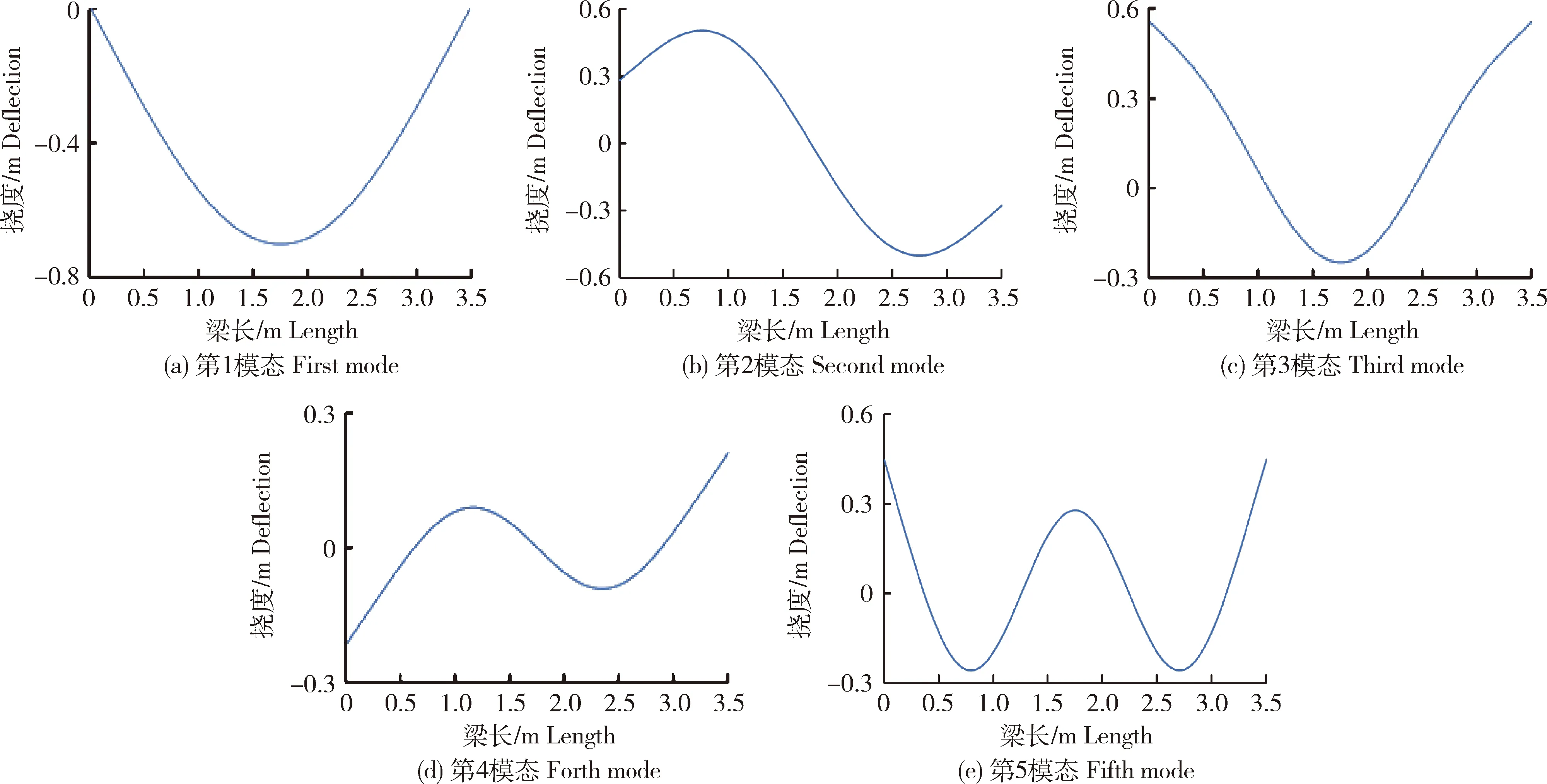
图3 组合地基梁前5模态的振型曲线Fig.3 The first five mode shape curves of combined foundation beams

为进一步研究组合地基梁的自振规律,本研究选取了10个结构模型,在总梁长不变的前提下,分别改变其沟宽尺寸和地基刚度,得到了各模型下的自振周期及对应的振型曲线。自振周期计算结果见表3。典型组合地基梁(模型4)和典型弹性地基梁(模型7)的振型曲线分别见图4和图5。由计算结果可以看出：组合地基梁的模态与普通等直梁的模态有明显差别,表现在不仅自振频率不同,振型分布也存在差异性。模型7为典型的弹性地基梁,前5阶振型曲线呈现典型的单一梁自振规律,其他所有组合地基梁的振型曲线分布均和全参数典型漏粪地板模型结果一致。其原因是,中间普通梁段的刚度较小,基本周期较大,在长周期状态下,弹性地基梁段尚未发生振动,中间普通梁段带动了两边地基梁段的振动,弹性地基梁段发生了近似刚体位移。

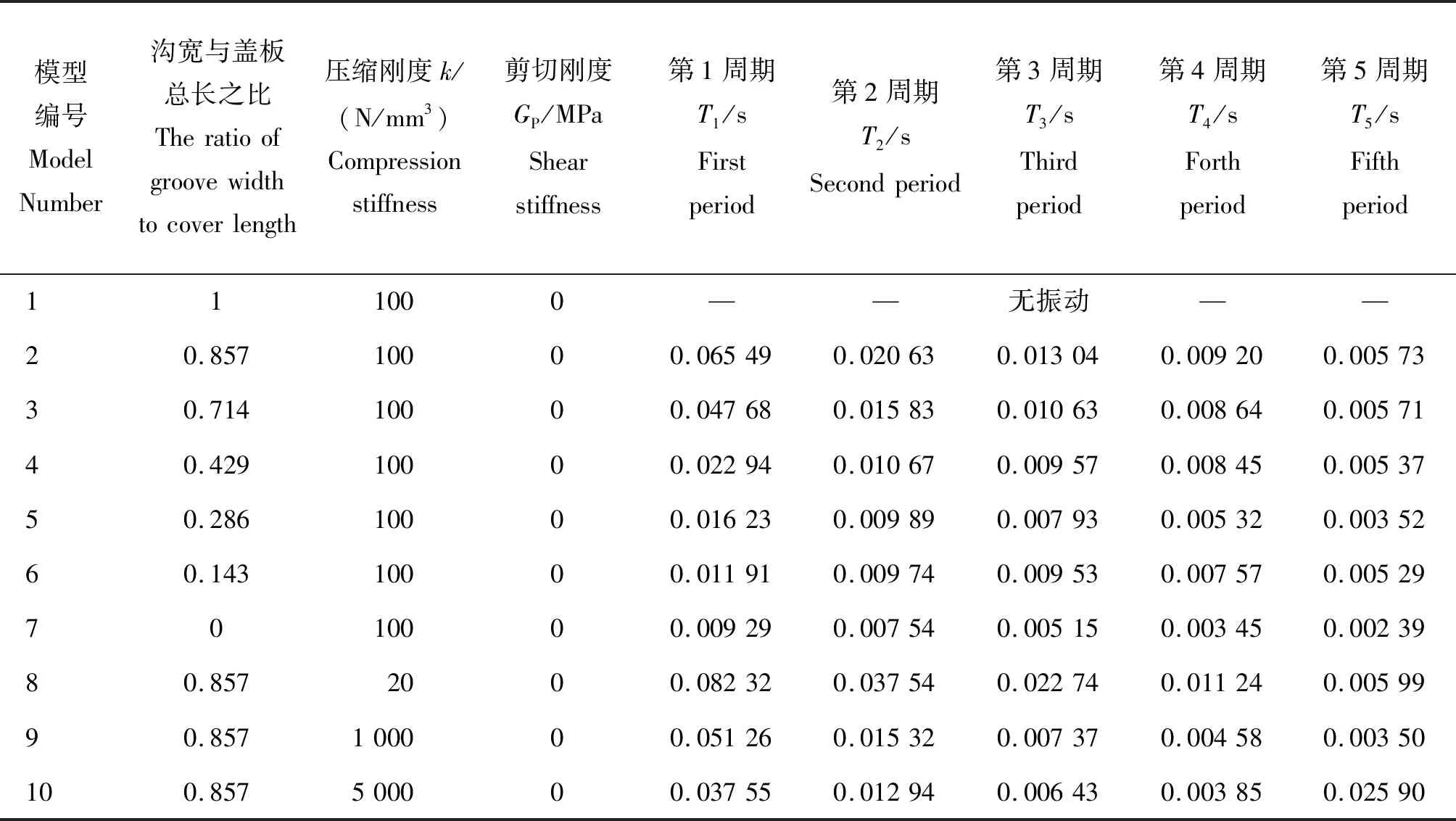
表3 组合地基梁不同模型结构参数及自振周期Table 3 Structural parameters and natural vibration period of different combined foundation beam models

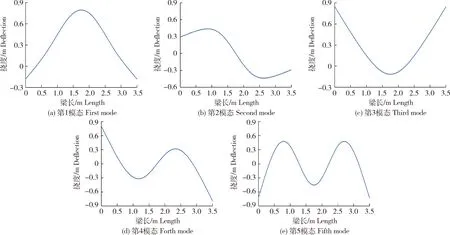
图4 模型4前5模态的振型曲线Fig.4 The first five mode shape curve of mode 4

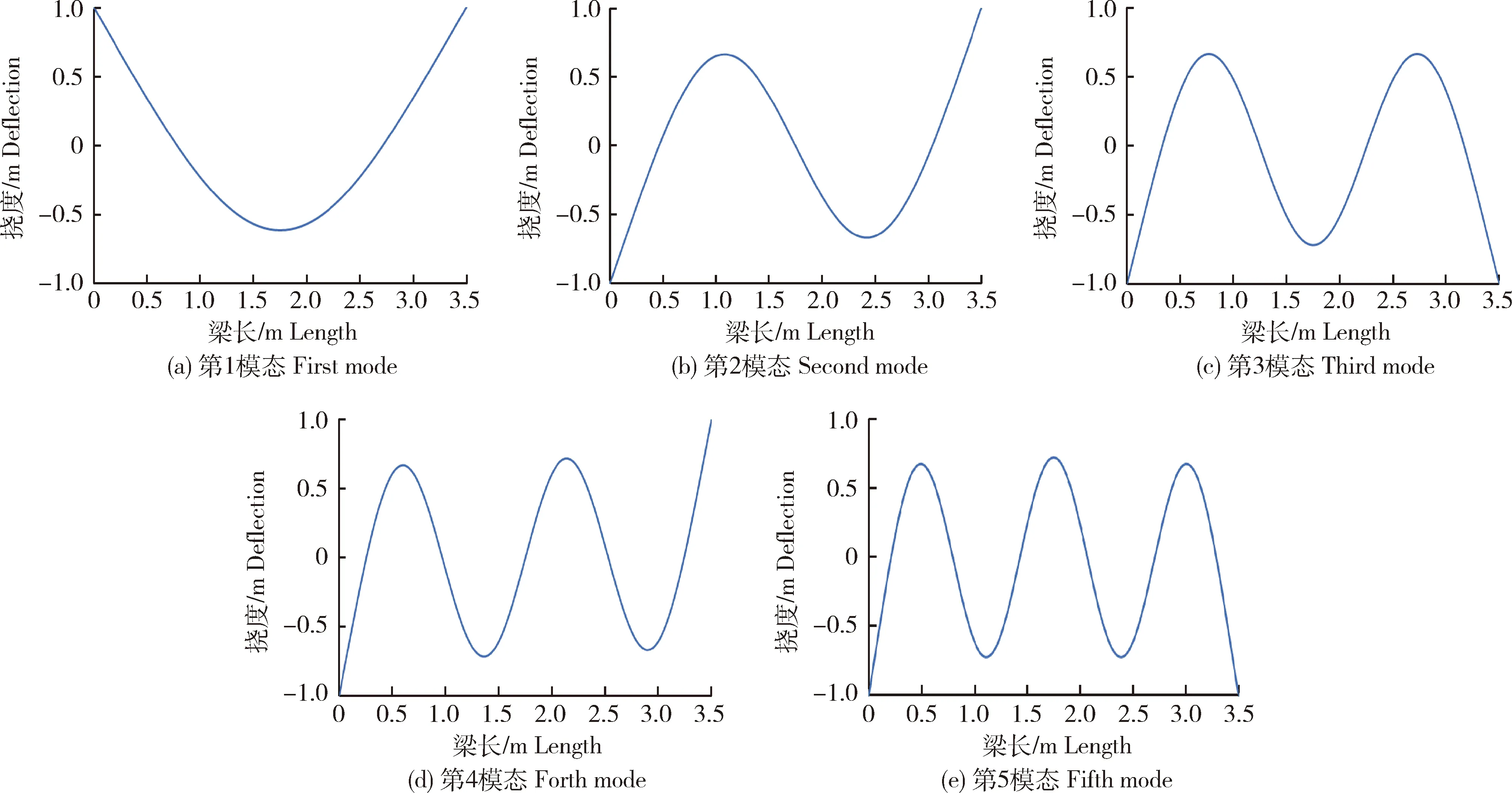
图5 模型7前5模态的振型曲线Fig.5 The first five mode shape curve of mode 7

3.2 漏粪地板自振周期

为得到典型钢筋混凝土漏粪地板的自振周期,本研究采用不同的分析模型,计算漏粪地板的自振周期。共选取了10种工况,其中工况1为简支普通等直梁模型。漏粪地板弹性模量E=32.5 GPa;剪切模量G=11.4 GPa;密度ρ=2 400 kg/m3;截面剪应力分布不均匀系数μ=1.2;沟宽lⅡ=3 000 mm;梁长l=2lⅠ+lⅡ;截面高度h=100 mm;支承长度lⅠ除工况4为500 mm外,其余均为250 mm;截面宽度b除工况3中bⅠ=bⅢ=125 mm外,其余均为100 mm。漏粪地板模型及结构参数见表4,自振周期计算结果见表5。由计算结果可以看出：

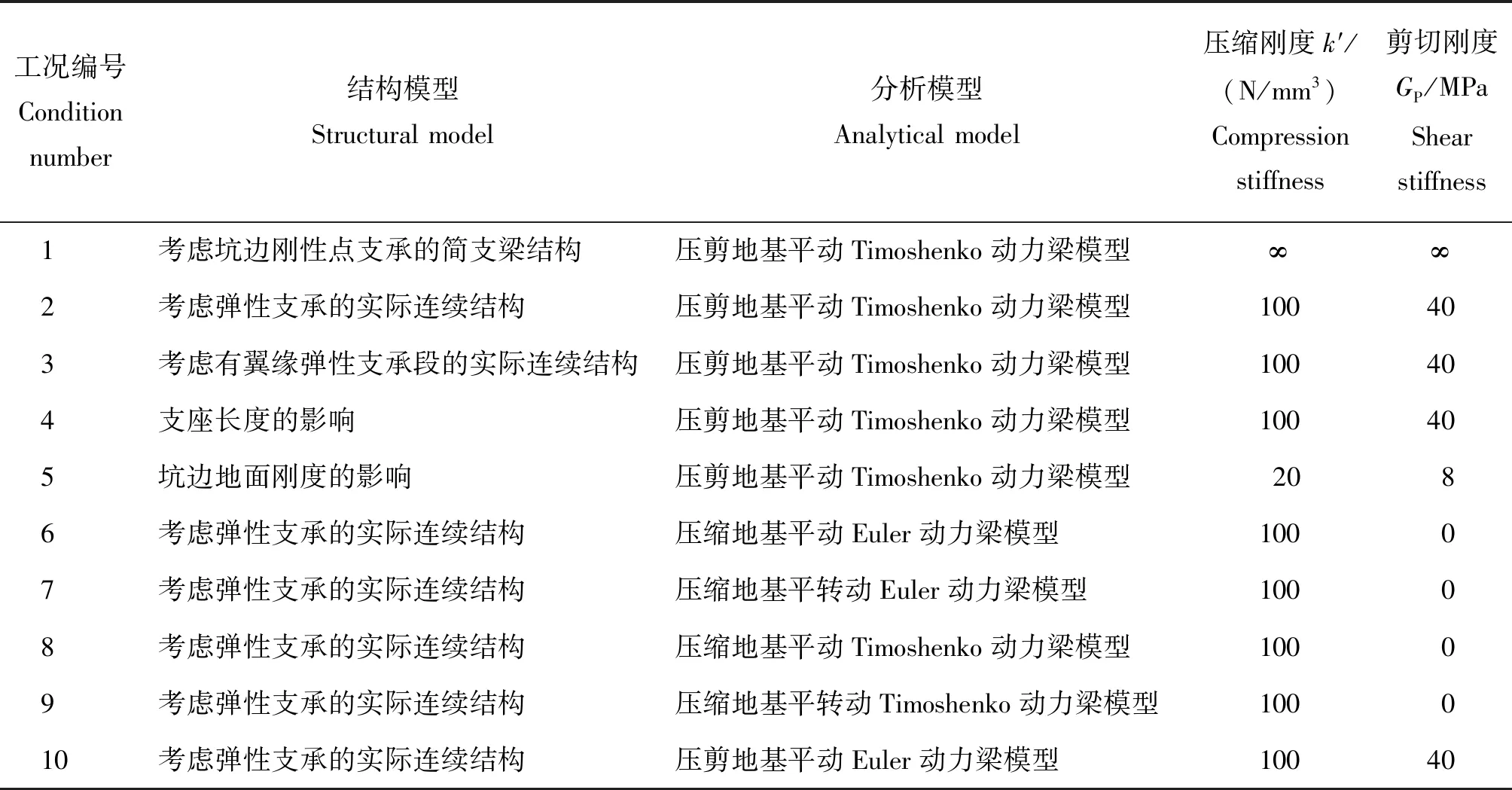
表4 漏粪地板模型及结构参数Table 4 Models and structural parameters of leakage floor

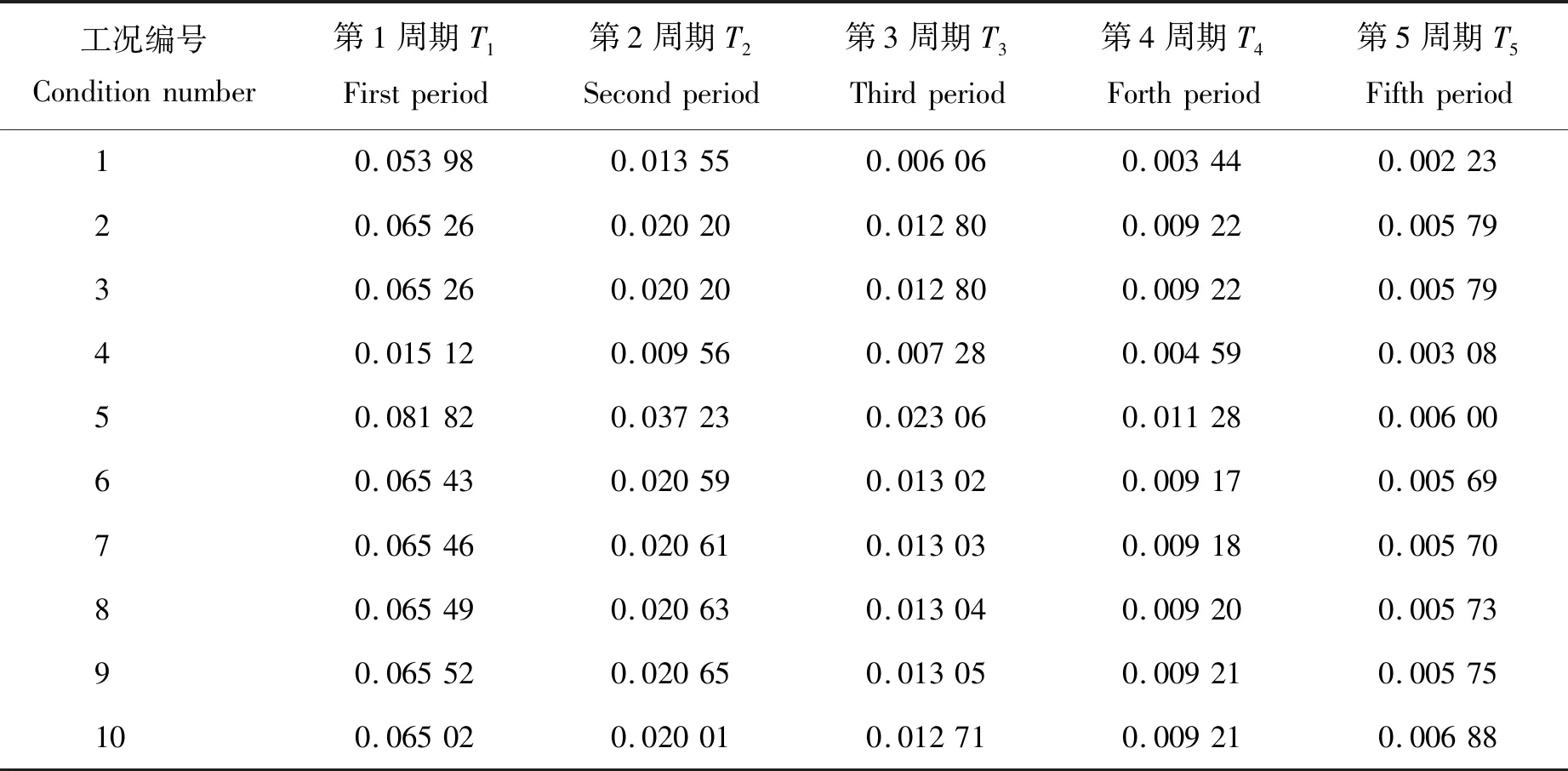
表5 漏粪地板自振周期Table 5 Natural vibration period of leakage floor s

1)工况1比工况2基本周期短17.29%,这是因为考虑坑边刚性点支承的简支梁结构忽略了地基的变形,导致梁支座刚度变大,自振周期减小明显;工况3与工况2的基本周期完全一致,这是由于板带模型宽度不改变板的振动特性;工况4比工况2基本周期短76.83%,这是因为支承长度的增加导致了组合地基梁支承刚度增加,自振周期减小。工程中,可以通过调整支承长度改变漏粪地板的自振周期,使其满足舒适性要求。

2)工况5比工况2基本周期长25.38%,随着地基压缩刚度的增大,漏粪地板自振周期的呈减小趋势,但减小渐缓,其原因是地基刚度的提高使得结构整体刚度随之增大,自振周期减小,但当地基刚度足够大后,地基变形增加不再明显,组合地基梁逐渐呈现出坑间简支梁的变形特征,因此可以通过改变地基垫层密实度来对漏粪地板进行振动控制;工况6和8及7和9对比发现Timoshenko梁模型比Euler梁模型的基本周期长0.09%左右,相差不大,其原因是Timoshenko梁模型考虑了剪切变形,使得结构刚度减小,自振周期增加,相差不大的原因是与跨度相比地板厚度较薄,剪切变形与弯曲变形相比可以忽略;工况6和7及8和9对比发现平转动模型比平动模型的基本周期长0.04%以内,相差细微,其原因是平转动模型考虑了转动惯性力,增加了结构的位移,导致结构刚度减小,自振周期增加,相差细微的原因是与跨度相比地板厚度较薄,截面抗弯刚度较小,转动惯性力与平动惯性力相比可以忽略;工况6和10及8和2对比发现压剪地基梁模型比压缩地基梁模型的基本周期短0.7%以内,偏差较小,其原因是压剪地基梁模型考虑了地基的剪切刚度,导致结构整体刚度增加,自振周期减小,偏差较小的原因是两端弹性地基梁段振型呈拟刚体运动特征,局部位移为直线分布,二阶导数近似为零,由于地基反力剪切项与竖向位移的二阶导数成正比,该分项较小,剪切引起的地基反力与压缩引起的地基反力相比可以忽略。

为反映漏粪地板自振周期和地基刚度的关系,根据表3中的计算结果,漏粪地板第1周期随压缩刚度的变化见图6。

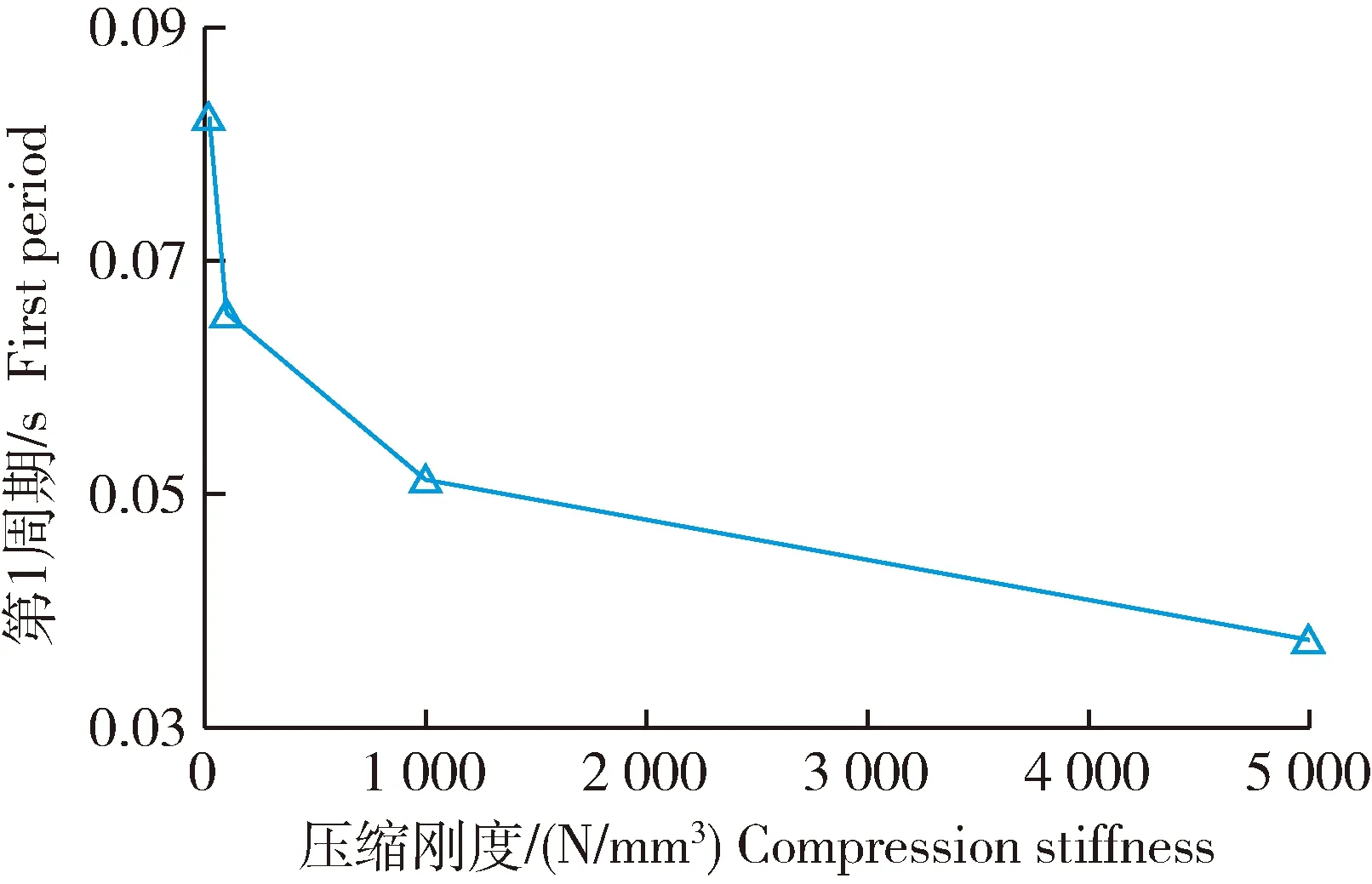
图6 漏粪地板第1周期随压缩刚度变化Fig.6 The curve of first period of the leakage floor with compression stiffness

3.3 简化漏粪地板自振周期计算方法

对漏粪地板进行自振周期分析时,在保证工程精度要求的前体下,应采用组合弹性地基梁模型,为计算简便考虑,可忽略端部缝间板条、梁的剪切变形、转动惯性力和地基的剪切刚度的影响。亦即采用压缩地基平动Euler组合地基梁模型对漏粪地板进行计算。

对于压缩地基平动Euler组合地基梁模型,其挠度基函数向量为：

(22)

由式(19)可得系数矩阵表达式为：

(23)

式中：ZvⅠ和ZvⅢ由式(17)得到,ZvⅡ由式(16)得到。

4 结束语

本研究综合考虑了地基的压缩和剪切刚度、梁的弯曲和剪切变形、运动的平动和转动惯性力以及轴力的二阶效应,建立了几何非线性压剪平转动Timoshenko弹性地基梁动力模型。给出组合地基梁自振特性计算方法,并对漏粪地板的自振特性进行了分析。研究表明,组合地基梁的自振特性与普通梁相比存在明显差异。各结构参数对组合地基梁的自振周期存在不同程度的影响：端部缝间板条无影响;支承长度及地基刚度影响明显,不可忽略;剪切变形、转动惯性力和地基的剪切刚度的影响较小,可以忽略不计。本研究建立的模型可对漏粪地板自振周期进行简化计算。