引入正弦余弦算子和新自花授粉的花授粉算法

张 超, 杨 忆

(1.宿州职业技术学院 计算机信息系, 安徽 宿州 234000;2.淮北师范大学 计算机科学与技术学院, 安徽 淮北 235000)

0 引 言

群智能优化算法作为人工智能学科一个重要分支,近年来该领域的研究比较活跃,新型的群智能优化算法不断涌现,如鲸鱼优化算法[1]、斑点鬣狗优化算法[2]、樽海鞘算法[3]、哈里斯鹰优化算法[4]、人工生态系统优化算法[5]、麻雀搜索算法[6]、政治优化算法[7]等。这些算法已帮助人们解决了现实世界的很多实际问题,如图像特征选择、芯片设计优化等[8]。基于“无免费午餐”定理,任何算法都不能适应于解决所有实际问题;在大数据时代,优化问题的决策变量与目标函数越来越多和复杂:这为新算法的提出和对现有算法的改进提供了更多研究空间。

花授粉算法(flower pollination algorithm,FPA)是YANG通过模拟自然界显花植物授粉过程,仿生设计的元启发式算法[9]。FPA只有一个全局搜索和局部开发转换的概率参数,结构简单,在处理低维优化问题时有较好的收敛精度,已在数据聚类[10]、机器人系统优化[11]等领域成功应用,但在处理高维优化问题时,亦存在收敛精度较低,易陷入局部极值等元启发式算法共有的缺陷。为了提高FPA的寻优性能,国内外学者使用不同的策略对其进行了改进:肖辉辉等将引力搜索算法融入FPA中,使用万有引力和FPA自身的Lévy飞行共同引导花粉个体位置更新,提升了FPA的寻优能力[12];李煜等使用反向学习策略初始花粉种群,采用逐维随机扰动策略更新自花授粉阶段的花粉个体位置,提高了FPA在求解大规模优化问题时的寻优性能[13];张慧颖等采用有利于全局广泛搜索的自适应移动因子提高FPA的收敛速度,并将其应用到室内可见光定位系统中[14];DRAA通过数值实验对FPA的性能做了详细的定量和定性分析[15];NABIL将FPA与克隆选择算法进行杂交,提高了算法的收敛精度[16];ABDEL-BASET等提出了一种复数编码的花授粉算法,将种群更新分为实部和虚部2个部分,以扩大个体基因中包含的信息量,进而增强花粉群体的多样性[17];NGUYEN等使用并行技术将花粉种群划分为若干亚种群独立迭代更新,以增强空间探索的多样性,使用紧凑技术减少算法在无线传感器网络节点优化过程中的存储变量和运行时间[18];OZSOYDAN等修改了非生物局部授粉的方式,并在算法的全局和局部授粉中采用了步长函数和随机因子,生成了基于物种的FPA[19]。

上述算法通过参数优化、与其他元启法式算法混合、采用不同编码方式、改进全局或局部授粉方式等策略对FPA进行了改进,并在实际应用中解决一些特定问题,取得了一定优化效果。不过,通过研究分析文献发现:①一些变体在不同程度地提升算法性能的同时,由于改进策略过于复杂,使得算法的计算复杂度大幅提升,导致算法的时间复杂度增加;②一些变体一定程度上提升了算法处理高维优化问题的寻优能力,但在一些经典的低维函数上的测试实验显示,其收敛精度甚至不如基本FPA算法,即改进算法失去了基本FPA处理低维优化问题的良好性能。

为了解决上述问题,本文提出一种引入正弦余弦算子和新自花授粉方式的改进算法(sine cosine flower pollination algorithm,SCFPA)。SCFPA做了2方面的改进工作:①使用振幅自适应指数非线性调整的正弦余弦算子,逐维扰动花粉个体以保持花粉个体的多样性;②基于优胜劣汰的自然法则思想,算法的自花授粉只在适应度排名在25%～75%之间的骨干花粉个体与前10%的精英个体之间随机展开,淘汰排名靠后的25%的劣质个体,防止“劣币驱逐良币”,以提高算法的寻优性能。

在9个基准测试函数上做仿真实验,验证了SCFPA的寻优性能和鲁棒性;并将其应用到悬臂梁设计、压力容器设计2个经典的机械工程实例上,验证了算法在解决实际工程问题时的有效性和实用性。

1 花授粉算法(FPA)

FPA是在4个理想规则[9]假设下,使用式(1)和式(3)分别模拟显花植物异花授粉和自花授粉过程,驱使花粉种群迭代更新,从而达到寻优的目的。FPA通过转换概率参数p控制算法进入异花授粉过程和自花授粉过程,即算法进行全局搜索和局部开发的转换。

(1)

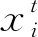
(2)

式中:λ=1.5;Γ(λ)为标准伽玛函数。

(3)

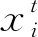
2 SCFPA改进策略

本小节介绍在异花授粉阶段和自花授粉阶段本文的改进策略以及SCFPA。

2.1 正弦余弦算子逐维扰动的异花授粉策略

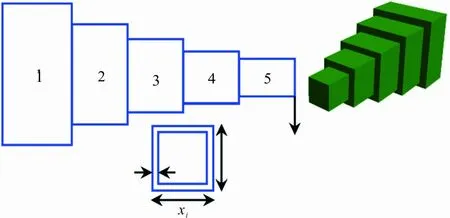
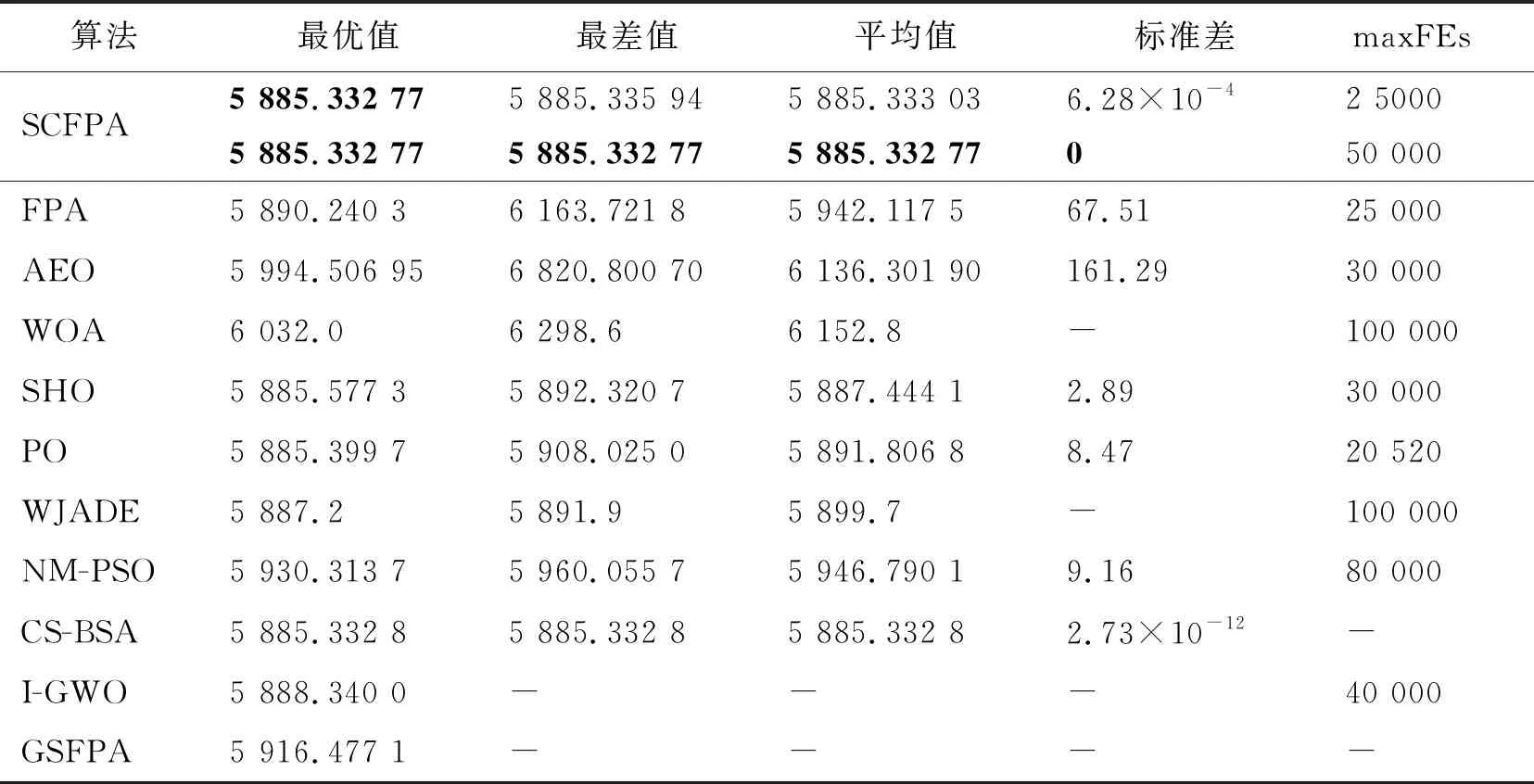
正弦余弦算法[20](sine cosine algorithm,SCA)是MIRJALILI于2016年,根据正弦余弦函数的周期性,提出的基于种群的群体智能优化算法。本文利用SCA中的正弦余弦算子对异花授粉阶段的花粉个体位置向量实施逐维扰动,并继承基本FPA以Lévy飞行向全局最优解方向迭代更新的策略不变。SCFPA通过定义正弦余弦算子转换概率参数Psc∈[0,1],将算法异花授粉阶段花粉位置的更新按2种方式随机进行:如果Psc

(4)

式中:A为正弦函数和余弦函数的振幅;a∈[0,2π]为服从均匀分布的随机数;L为Lévy飞行分布;g*为到当前为止最优花粉个体的位置;r∈[0,1]为服从均匀分布的随机数,控制算法以相等概率执行正弦算子或余弦算子。

算法迭代初期种群个体需在尽可能大的空间范围搜索,以勘探最有希望的区域;而在迭代中后期,种群个体应在最有希望的区域进行精细化搜索,以期收敛到最佳全局最优解。SCFPA中,这一过程通过正弦余弦函数设计自适应指数非线性调整的振幅模拟实现,使用式(5)计算。

A=β·exp(-100·(t/T)m)

(5)

式中:β为一个常量;t为当前迭代次数,T为最大迭代次数;m为形状调整参数,主要控制指数递减函数的下降速率。可根据实际优化问题设置合适的下降速率,m≥1,一般不超过3,如图1所示。随着算法的运行,振幅A可以以不同的下降速率自适应指数递减。

图1 不同下降速率的振幅A

式(4)对花粉个体位置向量实施正弦余弦算子逐维扰动变异,并继承基本FPA以Lévy飞行向全局最优解方向迭代更新的机制。在保持提升原算法寻优性能的同时,因正弦余弦算子的逐维扰动操作,有效增加了花粉种群的多样性,避免了算法因失去多样性而停滞收敛,进而达到提高算法性能的目的。

2.2 基于优胜劣汰法则的自花授粉策略

基本FPA中,自花授粉在任意2个花粉个体之间进行。因其选择的随意性,容易造成当前个体朝着不如自己适应度好的劣质花粉个体进化,进而导致算法收敛速度变慢,收敛精度下降,影响算法寻优性能。鉴于此,本文借鉴自然界优胜劣汰的生存法则思想,SCFPA的自花授粉只在适应度排名在25%～75%之间的骨干花粉个体与前10%的精英花粉个体之间随机展开,控制当前花粉个体不朝向适应度排名靠后的25%的劣质个体进化。该策略可以充分保持种群进化的优越性,充分发挥精英个体和骨干个体对种群的引领作用;同时,多精英个体的设置,又可避免算法陷入局部极值,提高收敛精度。此种策略与自然界中的真实授粉相符合,例如蝴蝶、蜜蜂等传粉者总是偏好造访花形大、颜色鲜艳的花朵,这样的花朵也优先得到授粉,繁育下一代。新的自花授粉策略计算方法为

(6)

2.3 SCFPA的执行流程

SCFPA的主要执行流程伪代码如下:

开始

算法参数设置:设置自花授粉和异花授粉转换概率参数P、正弦余弦算子转换概率参数Psc、常量β、形状调整参数m

在解空间随机初始化花粉种群

whilet

ifP

ifPsc

按式(1)更新异花授粉花粉个体位置

else

按式(4)更新异花授粉花粉个体位置

end if

else

按式(6)更新自花授粉花粉个体位置

end if

更新全局最优花粉适应度及位置

end while

2.4 SCFPA的时间复杂度分析

假设花粉种群规模为N,最大迭代次数为T,问题维度为D,转换概率参数为P。FPA重复执行的基本语句为异花授粉和自花授粉过程中花粉个体的位置更新语句。因此,根据时间复杂度运算规则,FPA异花授粉的时间复杂度为(N×D×T×P),自花授粉的时间复杂度为(N×D×T×(1-P)),二者合并后的FPA时间复杂度为(N×D×T)。

SCFPA自花授粉过程的算法结构与FPA一样,因此,自花授粉过程的时间复杂度为(N×D×T×(1-P))。SCFPA异花授粉阶段,由参数Psc控制分为2个过程随机进行,过程1的时间复杂度为(N×D×T×P×Psc),过程2的时间复杂度为(N×D×T×P(1-Psc)),二者合并后的SCFPA异花授粉的时间复杂度为(N×D×T×P),将SCFPA自花授粉和异花授粉的时间复杂度合并计算后(N×D×T)。因此,SCFPA与FPA属于同一数量级。

3 仿真实验与结果分析

3.1 测试函数和对比算法

在9个基准测试函数上做仿真实验,以客观评价SCFPA的寻优性能。9个测试函数的名称、变量区间、目标精度等信息见表1。

表1 基准测试函数

9个测试函数的具体表达式可参见文献[3-5]。其中,f1～f4为高维单峰函数,f5～f7为高维多峰函数,f8和f9为固定维度多峰函数。

对比算法包括基本FPA[9],花授粉的改进算法MFPA[16]和EOBLFPA[21],其他智能算法及其改进算法WOA[1]、SSA[6]、SCA[20]和灰狼优化算法的改进算法I-GWO[8]。通过对以上多元对比算法的选择,确保了充分客观地评价SCFPA的性能。

算法参数设置:SCFPA和FPA的自花授粉和异花授粉的转换概率参数设置一样,都为P=0.4。SCFPA的其他参数经数值实验得出:当β=6,在f1～f7高维函数上m=1,Psc=0.5;在f8～f9固定维度函数上m=2,Psc=0.1,此时算法的寻优效果较好。其他对比算法均使用对应参考文献推荐的参数设置。所有算法的种群规模为30,最大迭代次数为1 000。

3.2 与标准FPA的性能比较

与FPA进行比较时,在f1～f7高维函数上做维度分别为30、1 000和5 000的仿真实验,以侧重检验SCFPA在解决大规模优化问题(问题的决策变量,即维度大于等于1 000维以上[13])时的寻优性能。表2为2种算法分别独立运行30次的实验结果,其中“—”表示数据无法获得。下述各表格中,比较结果的较优值或最优值用黑体编排。

表2 SCFPA与基本FPA比较的实验结果

从表2可见,在高维单峰和多峰函数上,SCFPA在f1～f3、f5、f7等5个函数3种维度实验中每次都收敛到函数的理论最优值;在f4和f6函数上,SCFPA的各指标均明显优于FPA。从寻优精度与维度增长之间的关系看,随着维度大幅增长到1 000、5 000时,SCFPA的寻优精度基本不受影响,而FPA的寻优精度呈指数级增长,算法陷入了“维数灾难”。特别在f2上,维度增长到1 000维以后,FPA已不能进行寻优,而SCFPA仍能收敛到函数的理论最优值。可见,SCFPA较FPA在高维优化问题上的寻优性能得到大幅提升。

在f8和f92个固定维度多峰函数上,SCFPA在预设精度下的寻优成功率都为100%。从最小值、最大值、平均值和标准差指标可知,SCFPA每次都能收敛到函数的理论最优值,算法的鲁棒性较好。FPA虽能够收敛到函数的理论最优值,但从最大值、标准差和成功率指标看,FPA易陷入局部极值,算法不够稳定。

综上,SCFPA在高维上的寻优性能较FPA大幅提升,结论可拓展到有效求解问题维度达到1 000维以上的大规模优化问题;在低维上进一步增强了FPA的寻优性能。因此,本文提出的在异花授粉阶段引入正弦余弦算子策略,在自花授粉阶段引入基于优胜劣汰法则的新授粉方式策略,显著地提升了FPA的寻优性能。

3.3 与FPA改进算法和其他智能算法性能比较

表3是SCFPA与FPA改进算法,及近年出现的其他智能算法和改进算法的对比实验的结果,其中高维函数的维度为30。使用平均值和标准差作为算法性能评价指标;使用Wilcoxon秩和检验,做p=5%的显著性水平检验,验证实验数据的真实性,并决策SCFPA与对比算法的性能优劣:优于、劣于和相当于3种等级使用“+”“-”和“=”符号标记,决策结果在表3中最后一行列出。

从表3中可见:SCFPA在9个函数上均优于SCA、I-GWO和MFPA;SCFPA在8个函数上优于WOA,在f5函数上性能相当;SCFPA在6个函数上优于SSA,在f5～f7函数上性能相当;SCFPA在4个函数上优于EOBLFPA,在5个函数上性能相当,但EOBLFPA在固定维度多峰函数上易陷入局部极值,收敛精度较低。与多元的对比算法的比较结果表明,SCFPA具有显著寻优性能,在智能优化算法中具有竞争性。

表3 SCFPA与其他FPA改进算法和其他智能算法比较的实验结果

3.4 收敛曲线分析

限于篇幅,图2仅列出SCFPA和FPA、MFPA、EOBLFPA、I-GWO、WOA、SSA等对比算法在部分函数上寻优的收敛曲线。图2中,对所有函数的适应度值(F)做以10为底的对数处理。

从图2可见,SCFPA在f1、f2、f3、f5、f7上分别运行到大约170、220、150、40、40代,已经收敛到函数的理论最优值,收敛速度较对比算法优势明显。从SCFPA在f4函数上的收敛曲线可见,其收敛到的最佳精度优于所有对比算法。因此,进一步验证了本文提出的改进策略,有效地提升了基本FPA的收敛速度。

3.5 消融实验

均匀随机选择SCFPA的正弦算子或余弦算子,对花粉个体进行逐维扰动。将仅使用正弦算子,余弦算子扰动的算法分别记为SINFPA、COSFPA;将SCFPA与上述2种算法进行消融实验,结果见表4。

表4 正弦余弦算子消融实验结果

从表4可见:在高维函数上仅使用单一算子和均匀随机选择算子的寻优效果相当,但在固定维度多峰函数上,均匀随机选择算子较单一算子的扰动,使得算法性能稳定性有所提升。

4 SCFPA工程实例应用

机械工程约束优化是优化领域的一个重要分支,经典的机械工程实例常作为检验工程约束优化算法性能优劣的标准。应用SCFPA求解悬臂梁设计和压力容器设计2个著名机械工程实例,以检验算法的性能和解决现实世界中相似工程约束优化问题时的适用性。目前,公认的最有效的处理约束优化方法,是通过定义罚函数将约束优化转化为无约束优化求解。使用的罚函数定义为

(7)

式中:F(x)为罚函数;f(x)为原目标函数;φ≫1是惩罚因子,本文取φ=1030;n为约束不等式数量;gj(x)为不等式约束;

(8)

本文取k=2。

4.1 悬臂梁设计问题

悬臂梁由5个等厚空心砌块组成,其结构如图3所示。

图3 悬臂梁设计问题

梁为刚性支撑,垂直力作用于第5块的自由端。这个问题需优化5个构件的高度或宽度,使悬臂的总质量最小。该问题数学描述如下:

将SCFPA和FPA对悬臂梁问题求解的最优解与相关文献报道的SCAHGM[22]、SSA[3]、AEO[5]、GOA[23]、SOS[24]和MFA[25]等算法求解的最优解进行比较。为了客观公正地评价SCFPA,并使比较有意义,将SCFPA的种群规模设为20,最大迭代次数设为700,即最大适应度函数评价次数(maximum fitness evalutions,maxFEs)为14 000,比较结果见表5。

表5中“-”表示对比算法文献没有给出实验数据(下文同)。从表5可见,SCFPA明显优于FPA;在算法的最大适应度函数评价次数设置整体少于其他对比算法的情况下,除了SSA外,SCFPA求解的最优解优于所有其他对比算法,与SSA相当。对比结果说明,SCFPA在解决实际工程约束优化问题时具有一定优势。

表5 悬臂梁设计问题的最优解对比

4.2 压力容器设计问题

压力容器结构如图4所示。

图4 压力容器设计

压力容器共有4个设计参数,即半球形盖子厚度 (Th)、圆柱形管子内径(R)、圆柱形管子厚度(Ts)和长度(L)。设计目标是4个参数在满足一定约束条件下的总成本最少。该问题的数学描述如下:

其中(x1,x2,x3,x4)=(Ts,Th,R,L)。

约束条件:

g1(x)=-x1+0.019 3x3≤0,

g2(x)=-x2+9.54×10-3x3≤0,

g4(x)=x4-240≤0,

其中,0≤x1,x2≤99,10≤x3,x4≤200。

使用SCFPA求解该问题,程序独立运行30次。与解决该问题相关文献报道的AEO[5]、WOA[26]、SHO[2]、PO[7]、WAROA+JADE[26](简记为WJADE)、NM-PSO[27]、CS-BSA[28]、I-GWO[8]、GSFPA[12]等算法的结果进行了比较,比较结果见表6。

表6 压力容器设计问题的统计结果比较

为了使比较有意义,突出SCFPA的性能,将SCFPA的种群规模设为25,最大迭次数分别设为1 000和2 000,即maxFEs分别为25 000和50 000。从表6可见:在SCFPA的最大适应度函数评价次数为25 000,整体上远小于对比算法的情况下,除了CS-BSA外,SCFPA在4个指标上的值均优于所有对比算法,而且SCFPA的最优值优于CS-BSA;在评价次数提升到50 000次时,SCFPA在获得最佳解的同时,其标准差为0,优于所有对比算法,表现出了良好的稳定性。SCFPA获得的最佳解为:Ts=0.778 168 641,Th=0.384 649 163,L=200,R=40.319 618 72。

综上所述,SCFPA在求解2个经典机械工程优化问题上,在收敛到的最优解和稳定性方面优于文献报道的对比算法,说明SCFPA适应于求解现实世界的工程约束优化问题,具有良好性能。

5 结 语

花授粉算法在解决高维优化问题时,存在易陷入局部极值、收敛精度较低的缺陷。为此,本文在异花授粉阶段,引入振幅具有自适应指数非线性调整的正弦余弦算子,对花粉个体逐维扰动;在自花授粉阶段引入基于优胜劣汰生存法则的新授粉方式,对花授粉算法进行了改进。在9个包含高维单峰、多峰和固定维度多峰函数上的实验结果表明:SCFPA巩固提高了基本FPA处理低维优化问题的能力,大幅提升了处理高维优化问题的性能。在维度不小于1 000维,达到5 000维的大规模优化问题上,算法仍具有良好的寻优能力。在2个经典的机械工程实例上的实验结果表明:SCFPA在最大适应度函数评价次数远少于对比算法的情况下,收敛的精度和稳定性优于对比算法,说明SCFPA在处理实际工程问题时具有良好性能。鉴于SCFPA良好的大规模优化问题处理能力,后续将在解决具体的大规模应用问题上开展进一步研究。