基于PSO的GPC-PID的细纱机锭速控制算法

王延年,范 昊,李鹏程,王 栋

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

细纱机的卷绕成纱是纺纱过程中重要的一个环节[1]。纱锭的数量和纱线的断头率直接影响到纺织厂的效益,尤其是断头率对其影响极大。造成纱线断头的原因之一是在纺纱过程中,锭子无刷直流电动机转速波动较大,使纱线张力和强力的波动也随之增大,最终导致纱线出现断头[2]。

为了解决以上问题,人们采用不同的方法控制锭子的转速。文献[3]通过选用合适的材料对纺纱器械硬件设备进行升级改造,从而提高转速的稳定性。文献[4]采用子结构传递矩阵法计算出了锭子的转速范围,从而控制锭速。但是,这些控制方法不能实时地调控电动机的转速,并且不具备预测的功能,不能预知下一个周期系统的输出而提前调配参数,严重影响系统的稳定性和快速性,不能从根本上解决断头的问题。为此,本文提出了PSO算法优化GPC-PID控制算法来弥补以上方法的不足。

广义预测控制(generalized predictive control,GPC)是一种具有自适应功能的预测控制技术,能够很好地预测系统以后的输出,从而更好地对系统进行调控[5-6]。GPC是建立在一定模型的基础上,能够准确地预测未来的输出与对应的参数,然后将参数输入到传统的控制器中使之达到更好的控制效果,在控制领域颇受欢迎。文献[7-8]通过对GPC进行改进,预测PID的3个参数,虽然提高了系统的鲁棒性,但都存在一定的预测误差,导致整定的PID参数不精确;文献[9-10]分别用不同的方法改进广义预测,但是仍然存在以上的问题。PSO算法对目标函数和约束条件要求较低,同时也能较快地求解全局最优解,经常被用到处理各种优化难题当中[11-12]。因此,本文引入PSO算法解决广义预测算法预测精度低的问题。PSO算法优化GPC-PID算法首先对被控模型进行参数辨别,其次用PSO算法对广义预测算法进行优化得到最优控制参数,映射于PID控制器内,从而有效地控制电动机的转速与转矩脉动。采用该算法使锭子的转速与波动达到一个相对最优状态,这样纱线断头将会减少,达到本研究的预期目标[13-14]。

1 系统建模

1.1 细纱机工作原理

细纱机锭子结构图如图1所示。其工作原理为:粗纱经过粗纱管后,在纺纱段依靠前罗拉钳口进行拉伸变长; 拉长后的纱线通过导纱钩,穿过钢丝圈,最后紧密卷绕到锭子上的筒管上。

图1 细纱机锭子结构

1.2 电机数学模型

假定无刷直流电机的各项绕组对称,在不考虑各种非必要因素对参数影响的前提下,将无刷直流电机理想化,则BLDCM电压平衡方程为

(1)

式中:Ua、Ub、Uc为相电压;ia、ib、ic为相电流;ea、eb、ec为相反电动势;LM为每相绕组的自感与互感之差;r为电机相电阻;UN为中性点电压[15-16]。电机绕组星型连接相电流关系可表示为

ia+ib+ic=0

(2)

无刷直流电机电磁转矩与各相电流的关系可表示为

Te=(eaia+ebib+ecic)/ω

(3)

无刷直流电机运动方程可表示为

(4)

式中:Te为电磁转矩;TL为负载转矩;B为阻尼系数;ω为电机机械转速;J为电机转动惯量。

1.3 纺纱张力控制系统模型

卷绕电机的转速在不同的需求下设定为某一恒定值,在恒速运转期间希望纺纱张力保持恒定。但是,影响纺纱张力的因素有很多,例如气圈的大小、纱线是否有竹节、气圈的高度、锭子的转速等,其中最主要的影响因素是锭子的转速。因此,本文在假设其他影响因素不变的情况下,通过控制无刷直流电机的转速从而控制纱线的张力[17-18],并设计了如图2所示的恒张力控制系统。该控制系统由张力传感器、张力与速度对应转换机制和放大器组成。检测装置测量纺纱张力T,并将测得的张力由计算机转换为对应的速度信号v,与给定的速度v*作差输入到控制器中;控制器对其运算可得到所需的控制量u,控制逆变电路的输出电压,用于控制BLDCM的转速。从而更好地控制纱线张力,使张力达到一个不变的状态[19]。

图2 纱线恒张力控制系统流程

2 PSO算法优化GPC-PID控制器设计

2.1 PSO算法

PSO算法的作用是寻找整个过程的最优解。该优化算法是由多个粒子在一定的范围内运动,受粒子自身的最佳过去位置和整个群体的最佳过去位置的影响,最终在整个空间中寻找到具有最优解的粒子[20-21]。粒子的速度及位置更新公式[22-23]如下:

(5)

(6)

2.2 GPC-PID算法

GPC对模型参数要求少,更具有鲁棒性,并且能够实时地预测和优化未来,更适合应用在工业控制中[24]。GPC的结构如图3所示。

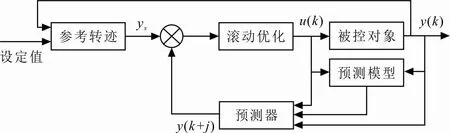
图3 GPC结构

1) 预测模型。GPC采用了受控自回归积分滑动平均模型,即

(7)

式中:z-1为后移算子;Δ=1-z-1为差分算子;ξ(k)为均值为零的白噪声序列。为了验证式(7),这里将设定c(z-1)=1。为了求出j步后输出y(k+j|k)的值,考虑下述丢番图方程:

1=Ej(z-1)A(z-1)Δ+z-jFj(z-1)

(8)

式中:Ej(z-1),Fj(z-1)只由表达式A(z-1)和j决定。其关系可以表述为

Ej(z-1)=ej,0+ej,1z-1+…+ej,j-1z-(j-1)

Fj(z-1)=fj,0+fj,1z-1+…+fj,naz-na

给式(7)两边同时乘以Ej(z-1)Δ并利用式(8),可得k+j时刻的输出关系式:

y(k+j|k)=Ej(z-1)B(z-1)·

Δu(k+j-1|k)+Fj(z-1)y(k)+

Ej(z-1)ξ(k+j)

(9)

由于ξ(k+j)未知,因此可以将其忽略不计,则y(k+j)最佳的预测值为

Δu(k+j-1|k)+Fj(z-1)y(k)

(10)

记Gj(z-1)=Ej(z-1)B(z-1),则根据式(10)可得

Fj(z-1)y(k)

(11)

2) 滚动优化。在GPC中,k时刻的性能指标具有以下形式:

(12)

其中,

ys(k+j)=αjy(k)+(1-αj)yr

(j=1,2,…,n)

式中:E(·)表示取数学期望;ys(k+j)为未来输出的参考轨迹;N1和N2分别为预测时域的开始和停止时刻;Nu为控制时域,u(k+j-1)=u(k+Nu-1|k),j>Nu;λ(j)为控制加权系数,一般取λ(j)=λ;y(k)、yr分别为输出、设定值;α为柔化系数,0<α<1。

利用预测模型式(11),可以得到

GN(z-1)Δu(k+N-1|k)+FN(z-1)y(k)=gN,0Δu(k+N-1|k)+…+gN,N-NuΔu(k+Nu-1|k)+…+gN,N-1Δu(k|k)+fN(k)

(13)

其中,

fN(k)=zN-1[GN(z-1)-

z-(N-1)gN,N-1-…-gN,0]·

Δu(k+N-1)+FN(z-1)y(k)

如果记

Δu(k|k)=

(Δu(k+1-1|k),…,Δu(k+N2-1|k))T

f(k)=(fN1(k),…,fN2(k))T

则可得

y(k|k)=GΔu(k|k)+f(k)

(14)

其中,

从而把式(12)性能指标写成向量形式:

J(k)=(y(k|k)-w(k))T·

(y(k|k)-w(k))+

λΔu(k|k)TΔu(k|k)

(15)

式中:

w(k)=(ys(k+N1),…,ys(k+N2))T

最优控制量为

Δu(k)=(1,0,…,0)(λI+GTG)-1GT·

(w(k)-f(k))

(16)

3) 在线辨别与校正。由于预测值随时都会受到环境因素的影响,因此引入在线辨识与校正,式(7)可转换为

Δy(k)=-A1(z-1)Δy(k)+

B(z-1)Δu(k-1)+ξ(k)

(17)

其中,A1(z-1)=A(z-1)-1。

把式(17)中的各种参数分别用向量表示为

θ=(a1,…,ana,b0,…,bnb)T

φ(k)=(-Δy(k-1),…,-Δy(k-na)·

Δu(k-1),…,Δu(k-nb-1))T

用渐消记忆的递推最小二乘法估计参数矢量:

(18)

式中:0<μ<1为遗忘因子;K(k)为权因子;P(k)为正定矩阵。在控制的每一步,首先要组成数据向量,根据式(18)可以求出θ(k)、K(k)、P(k),再根据各种参数的向量表示形式可得到A(z-1)、B(z-1)的参数,然后重新计算式(16)求出Δu(k)。

增量式数字PID控制算法表达式为

u(k)=u*(k-1)+kp[e(k)-e(k-1)]+

kie(k)+kd[e(k)-2e(k-1)+

e(k-2)]

(19)

其中u*(k)为控制量。定义

(20)

其中,

将式(19)、(20)改写成如下的形式:

u*(k)=u*(k-1)+L(k)TE(k)

(21)

结合式(15)和(21),得

J(k)=(y(k|k)-w(k))T(y(k|k)-w(k))+

λE(k)TL(k)L(k)TE(k)

(22)

令∂J(k)/∂L(k)=0,化简得优化解

(23)

通过得到的解便可得到控制器参数l1(k)、l2(k)、l3(k),从而得到PID控制器参数kp(k)、ki(k)、kd(k)[25]:

(24)

2.3 PSO算法优化PID-GPC

PSO算法优化的最终效果是使适应度函数f(k)取得最大值,而GPC-PID算法预测的最终目标是使得J(k)达到最小。为了满足2种算法各自的要求,将函数f(k)用式(25)表示,f(k)的取值范围为[0,1][26]。

(25)

根据式(25),对目标函数优化,使之满足上述要求,并求得最优的控制增量Δu(k)。此时将求出的Δu(k)以及y(k)和yr(k+1)代入式(23)中L(k)求出l1(k)、l2(k)、l3(k),根据式(24)即可得到kp(k)、ki(k)、kd(k)。PSO算法优化GPC-PID的流程如图4所示。

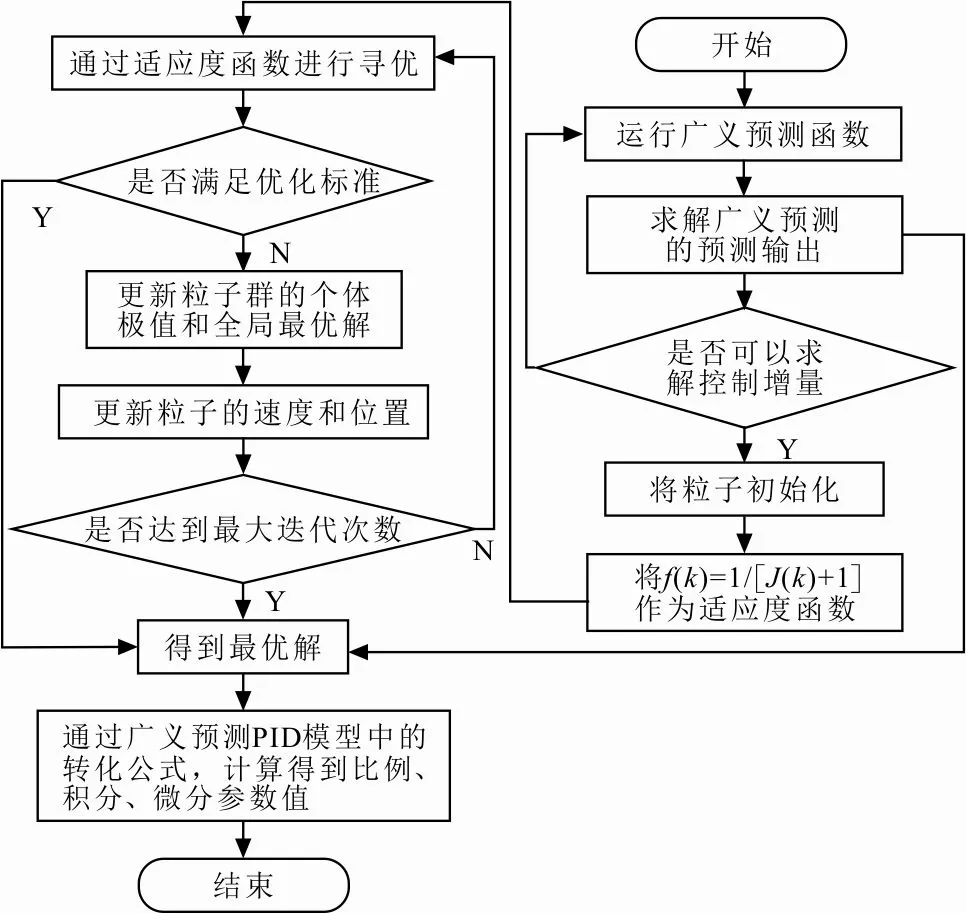
图4 PSO算法优化GPC-PID的流程

通过PSO算法优化GPC-PID,能够很好地将PSO和GPC-PID统一起来,发挥2种算法共同的优点。该控制器的控制量u(k)对应的是驱动电路中电流给定值I*。由于微分环节存在对高频噪声比较敏感且容易将噪声干扰扩大的不足,所以在PSO算法优化GPC-PID控制器后再加入一个内环电流PI调节器,从而计算出逆变电路所需要的输入电压U对电机进行调速,同时能够有效地消除微分带来的不利影响。锭子无刷直流电机双闭环控制系统如图5所示,图中虚线框内为GPC-PID控制器。

图5 无刷直流电机控制系统

3 实验结果与分析

为了验证本文所提出的PSO算法优化GPC-PID算法的效果,在MATLAB/Simulink中搭建BLDCM调速系统的模型并对其进行仿真,比较无刷直流电机调速系统分别在PSO算法优化GPC-PID算法和传统的GPC-PID算法的控制下的运行状况。选取额定电压24 V,额定电流1.5 A,极对数P=4,转矩系数0.035 N·m/A,阻尼系数B=0.01,采样时间T=0.000 1 s的三相无刷直流电机;选取广义预测参数N1=1,N2=6,Nu=2,α=0.995;选择种群规模为80,迭代次数为100次,c1=c2=2,惯性权重初始值Ws=0.9,惯性权重结束值We=0.4。

1) 系统的快速性与稳定性。设定无刷直流电机进入稳定状态时的转速为18 000 r/min,带负载TL=100 mN·m运行,模拟卷绕细纱过程。图6和7分别是电机在2种算法控制下转动开始时的转速变化轨迹和电机进入稳定状态时的转速变化轨迹,电机在2种算法控制下启动和稳定时的性能指标如表1所示。

图7 电机进入稳定状态时转速响应曲线

表1 电机启动和稳定时的性能指标

由表1可知:电机在传统的GPC-PID控制下调节时间较长,快速性略差,波动范围较大,超调量较大,速度最终稳定在18 100 r/min上下,稳定性较弱,与设定值存在较大的偏差; 而在PSO算法优化GPC-PID算法的控制下,波动较小,调节时间较短,收敛速度快,快速性好,并且电机转速的超调量较小,最终电机转速稳定在18 000 r/min上下,稳定性好,更加接近设定转速,比传统的GPC-PID控制效果更好。

2) 系统的抗干扰能力。运行时间为3.4 s时对系统输入干扰信号(将负载改为TL=150 mN·m),电机转速响应曲线如图8所示,电机在2种算法控制下遇扰动时的性能指标如表2所示。

图8 电机遇扰动时转速响应曲线

表2 电机遇扰动时的性能指标

由表2可知:当电机在工作时突遇一个扰动,在传统的GPC-PID算法控制下,虽然电机在遇到扰动时能恢复到稳定状态,但是用时较长,且波动较大,抗干扰性与稳定性较差; 而在PSO算法优化GPC-PID控制的电机在经历短暂的波动后,转速很快恢复到稳定状态,用时比前一种算法短,且波动较小,抗干扰性与稳定性较前一种算法都比较强,控制效果优于传统的GPC-PID控制。

4 结 语

为了提高纺织厂细纱的产量与质量,本文依据无刷直流电机的工作原理,从控制细纱机锭速入手,提出了基于PSO的GPC-PID算法。通过广义预测算法实时整定参数,并且采用粒子群算法对广义预测进行优化,最终使无刷直流电机的转速更加稳定,抗干扰能力加强,波动较小,减小了纱线的张力,降低了细纱卷绕过程中的断头率,提高了细纱产量。