基于分形齿面粗糙度的双渐开线齿轮时变啮合刚度研究
陈 亮, 樊智敏, 尹兆明, 曲 伟, 张耘瑞
(青岛科技大学 机电工程学院, 山东 青岛 266061)
传统的齿轮时变啮合刚度计算采用能量法[1-2]与有限元法[3-4],大部分未考虑到齿面形貌对齿轮时变啮合刚度的影响.齿轮由于其加工特点,齿面通常会存在一定的粗糙度,类似于许多微凸体在齿面分布,这一齿面形貌具有微凸体在小区域内随机分布、在整体范围内却自相似性分布的特征,因此运用M-B分形理论对啮合刚度进行研究可以从理论上系统地分析齿面形貌参数对齿轮啮合刚度的影响.
目前通过分形理论求解结合面接触刚度的研究已取得了诸多成果.张学良等[5]提出了根据分形理论的机械结合面法向接触刚度求解模型,并进行了试验验证.Buczkowski等[6]通过W-M函数对已有分形模型进行修正,提出了基于分形理论的结合面法向接触刚度求解的新型模型,并对粗糙平面试件进行了试验,验证了模型合理性.黄康等[7]基于分形理论,通过分析一对圆柱体之间接触与分形理论中假设模型接触的不同,构建了表面接触系数表达式,提出了一对圆柱体之间接触的分形接触模型.李小彭等[8]考虑摩擦因素,给出了含摩擦系数的微凸体由弹性变形到塑性变形时临界变形面积公式,剖析了摩擦系数等参数对系统不稳定性的影响.
随着研究的不断深入,部分学者将分形理论运用到齿轮啮合刚度求解研究当中.刘鹏等[9]结合分形理论在圆柱体表面接触的应用,考虑齿面摩擦以及齿面微观因素等,求解了微线段齿轮的啮合刚度.王晓鹏等[10]结合分形理论在圆柱体表面接触应用,计算了发生微点蚀的齿轮啮合刚度.杨荣松等[11]采用W-M函数与曲面分形接触模型,给出了考虑摩擦系数、不同曲率半径和粗糙度的摆线针轮接触刚度分形模型.
双渐开线齿轮是综合渐开线齿轮与圆弧齿轮优点的一种新型齿轮[12],其齿廓包含上下齿面渐开线、连接两段渐开线的齿腰过渡曲线和齿根过渡曲线,因其啮合传动时齿腰分阶位置轮齿不参与啮合,一般制成斜齿轮.由于渐开线斜齿轮副与双渐开线齿轮副不能直接等效为圆柱体接触,所以上述研究方法并不能很好地应用于这类齿轮啮合刚度分析.目前,双渐开线齿轮接触问题通常等效为一对反向阶梯圆锥滚子接触进行分析[13],并主要采用赫兹接触理论与有限元法[14-17]对齿轮接触特性研究,未考虑齿面形貌对齿轮接触特性的影响.由工程实践可知,齿面形貌是影响齿轮摩擦磨损和接触疲劳等性能至关重要的因素[18].本文中考虑齿面微观形貌与摩擦,结合一对反向阶梯圆锥滚子接触模型,将每一啮合时刻下齿轮接触线“分段”,每段接触线上的接触等效为圆柱体接触,并基于M-B分形理论与赫兹接触理论,建立考虑分形齿面粗糙度的双渐开线齿轮时变啮合刚度模型,分析齿面形貌参数与摩擦系数等对齿轮时变啮合刚度的影响.本文中所建立分形模型对双渐开线齿轮时变啮合刚度预估与齿轮加工工艺及材料选取等提供了理论依据.
1 双渐开线齿轮粗糙表面接触模型
1.1 双渐开线齿轮副的真实接触面积
双渐开线齿轮基本齿廓参数如图1所示,mn为法面模数;αa和αd分别为齿顶区域和齿根区域齿形角;和分别为齿顶区域和齿根区域切向变位系数;l∗a和分别为齿腰过渡圆弧齿顶区域和齿根区域高度系数;ρg和ρf分别为齿根区域和齿腰区域过渡圆弧半径;为齿顶高系数;c*为顶隙系数.
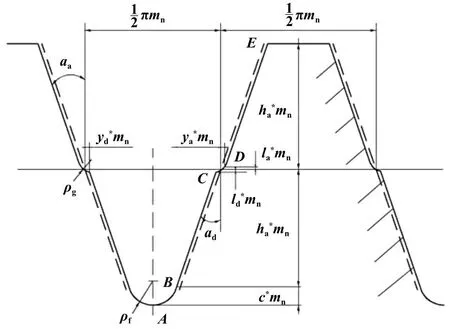
Fig.1 Basic tooth profile of double involute gear图1 双渐开线齿轮基本齿廓
双渐开线齿轮副中一对轮齿在t时刻啮合时,可近似等效为一对反向阶梯圆锥滚子接触[13],如图2所示.考虑齿轮在啮合过程中轮齿齿面上相同啮合时刻下不同啮合位置以及不同啮合时刻下相同啮合位置的啮合状态均表现出一定的差异.考虑粗糙齿面接触,结合M-B分形理论与圆柱体分形接触模型,为研究一对轮齿在t时刻沿接触线方向不同位置接触问题,图2中将其沿接触线li(t)等效为m对圆柱体接触,第j对圆柱体的半径分别为主动轮曲率半径和从动轮曲率半径,有效接触长度为,ω1为主动轮旋转角速度,ω2为从动轮旋转角速度.
图3所示为t时刻双渐开线齿轮接触线在基圆柱上的展开图,其中CDC'D'区域为齿腰分阶位置轮齿不参与啮合区域,βbp和βbg为基圆螺旋角,Pbt为端面基节,B为齿宽.
双渐开线齿轮端面重合度大于轴向重合度时,接触线li(t)长度可表示为
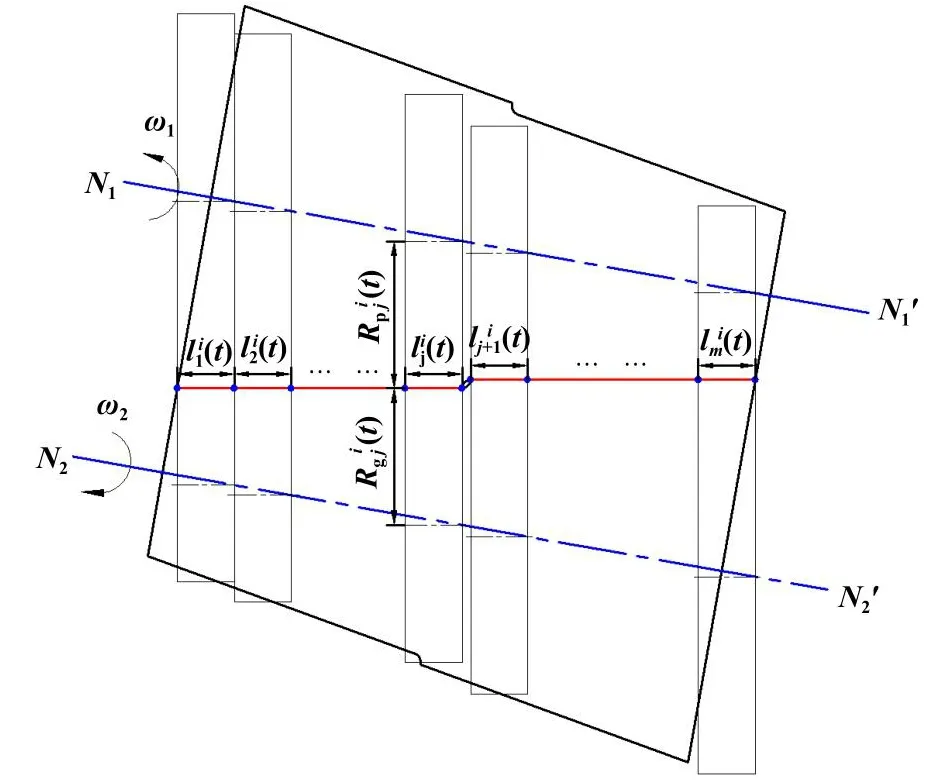
Fig.2 Simplified contact model of a pair of reverse step tapered rollers图2 简化后一对反向阶梯圆锥滚子接触模型
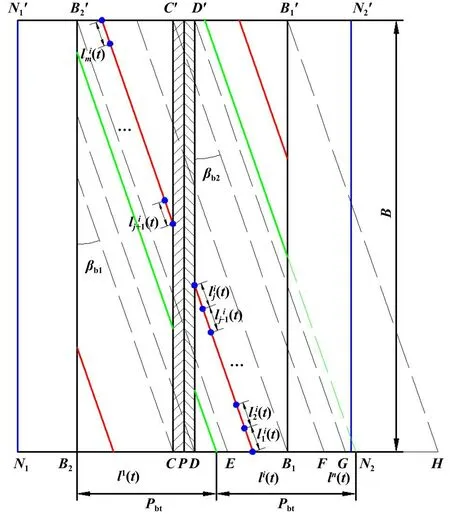
Fig.3 Expanded view of contact on the base cylinder图3 接触线在基圆柱上展开图
式中:rb1为主动轮基圆半径,N1N1'N2N2'为理论啮合区域,B2B'2B1B'1为实际啮合区域,N1和N2分别为齿轮的理论啮入点和啮出点,P为节点,B2和B1分别为齿轮的实际啮入点和啮出点,C和D分别为齿根分阶点和齿顶分阶点,E、F、G和H分别为接触线变化的特殊节点,Δl为齿腰分阶位置损失掉的接触线长度[19],
基于接触线百分比法,t时刻第i条接触线上第j段上的载荷为
式中:Pn为法向载荷,Pn=Tp/(rbp·cosβbp),Tp为主动轮输入转矩,rbp为主动轮基圆半径,假定t时刻下有n对轮齿同时啮合,LZ(t)为t时刻总接触线长度为
主动轮曲率半径为
式中:l为t时刻第i条接触线上第j段沿接触线方向到N1N2的距离,lCC′、lDD′以及l≥lB1B′1分别为t时刻第i条接触线沿接触线方向从N1N2到CC'、DD'以及B1B'1的距离.
M-B分形理论中所给出的模型是将粗糙表面的接触简化为1个粗糙平面与1个理想光滑平面之间接触,考虑到等效模型为m对圆柱体接触,引入表面接触系数[20](t)为
式中:E为齿轮综合弹性模量,E=1/[(1−)/Ep+(1−)/Eg],Ep为主动轮弹性模量,Eg为从动轮的弹性模量,υp为主动轮的泊松比,υg为从动轮的泊松比.
结合圆柱体分形接触模型,接触线li(t)上第j对等效圆柱体粗糙表面接触的微凸体分布函数nij(t,a)为
式中:a为此对圆柱体接触面上微凸体接触面积,为此对圆柱体接触面上微凸体最大接触面积,D为分形维数,Ψ为齿面微凸体大小位置分布的域扩展因子,物理意义见文献[21],其满足下列超越方程:
1.2 考虑粗糙度的法向载荷
在M-B分形接触模型中,微凸体未发生接触时的二维形貌可由如下数学表达式[22]拟合:
式中:G为粗糙度幅值.
由式(12)可知,微凸体接触变形量δ为
根据文献[8]可得,考虑摩擦的情况下,双渐开线齿轮齿面上微凸体在接触过程中由弹性变形转变为塑性变形时的临界面积ac为
式中:ϕ为双渐开线齿轮材料的特性参数,ϕ=σy/E,σy为双渐开线齿轮材料屈服强度,kμ为摩擦力修正因子,其表达式为
式中:μ为摩擦系数.
通过赫兹理论与式(13),可以得到齿面上单个微凸体在弹性变形时载荷表达式为
当齿面接触过程中,齿面上微凸体实际接触面积最大值al大于齿面上弹塑性变形临界面积ac时,其处于弹塑性变形阶段;当al小于ac时,其处于塑性变形阶段.根据式(8)、式(14)和式(16)可推导t时刻接触线li(t)上第j对等效圆柱体真实接触面积与载荷关系如下:
当al>ac时:
①D≠1.5
②D=1.5
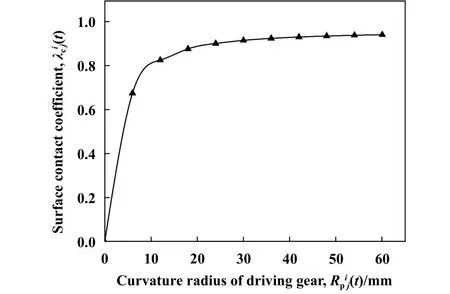
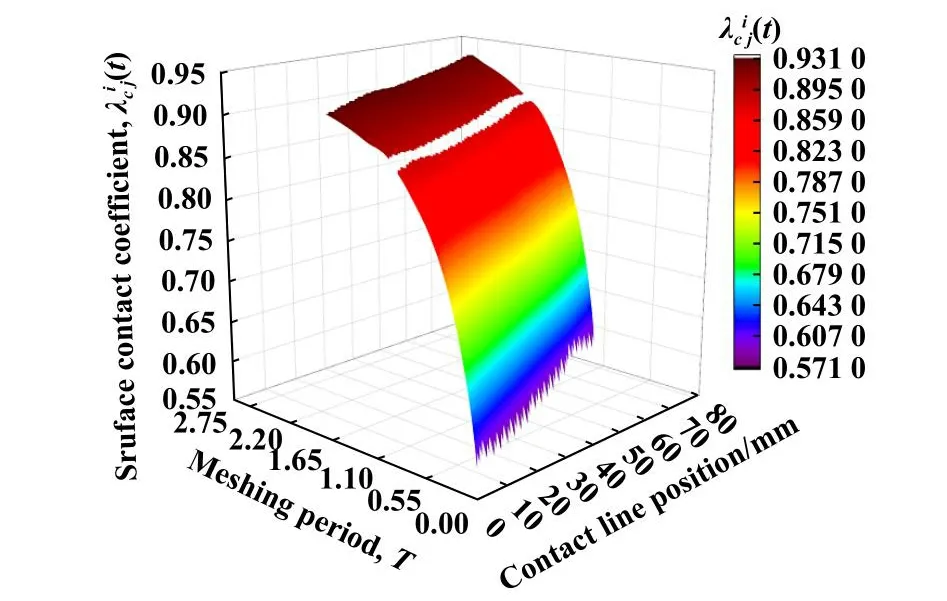
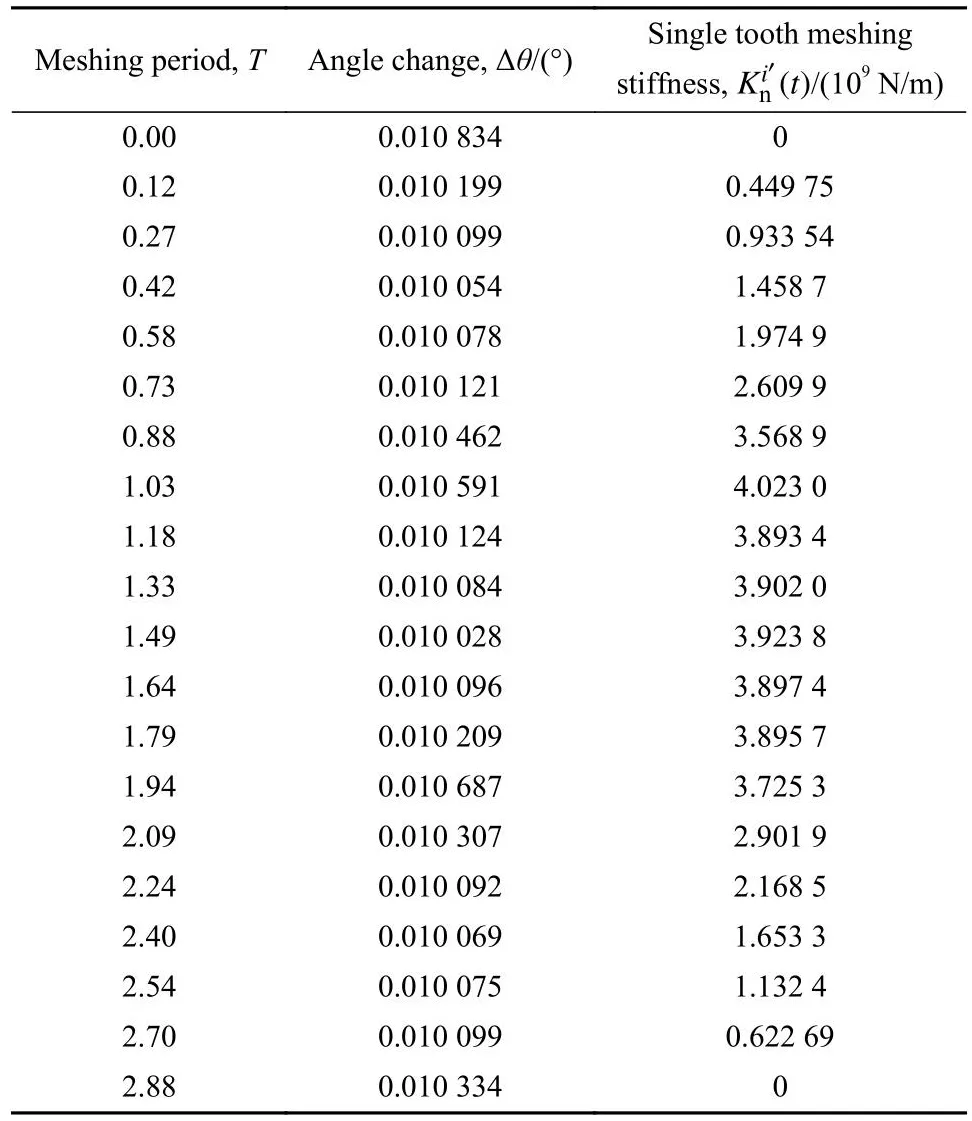
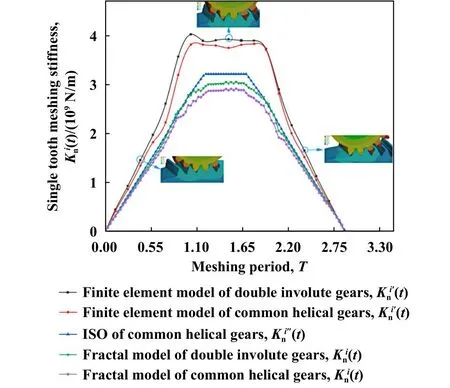
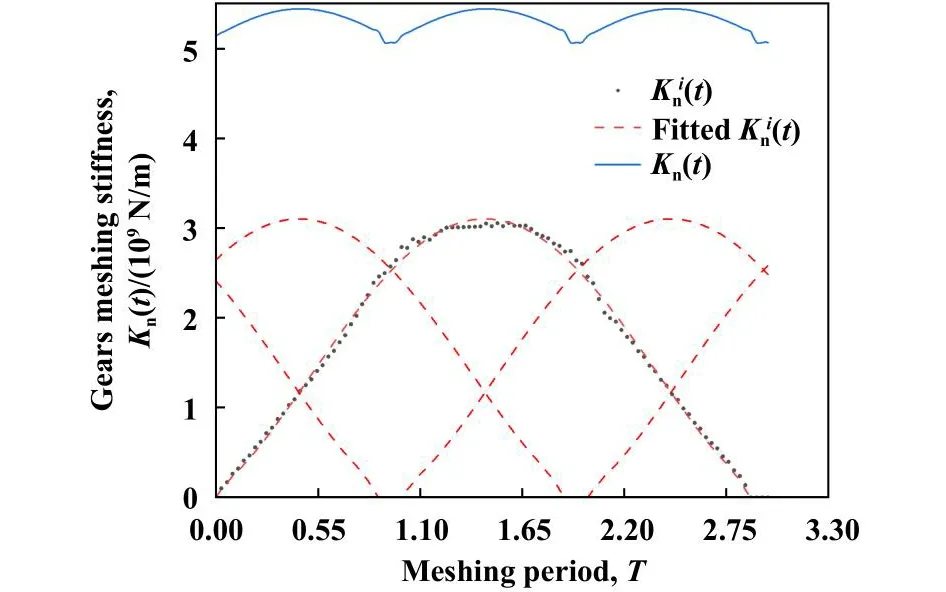
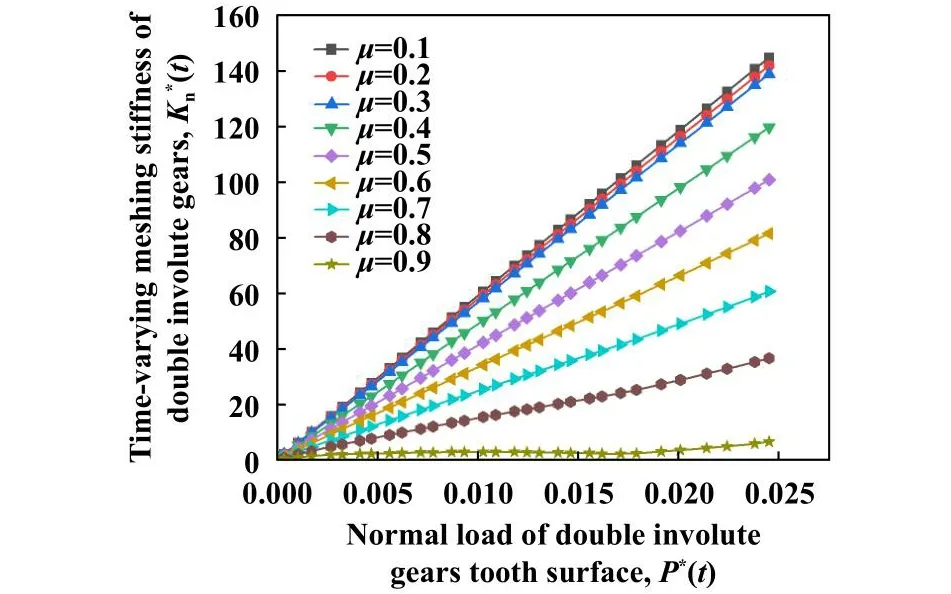
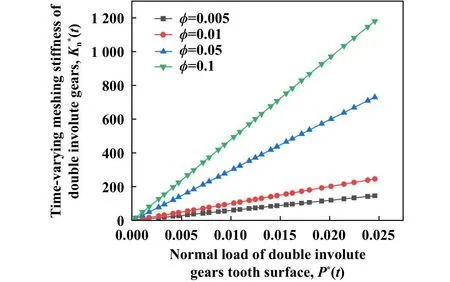
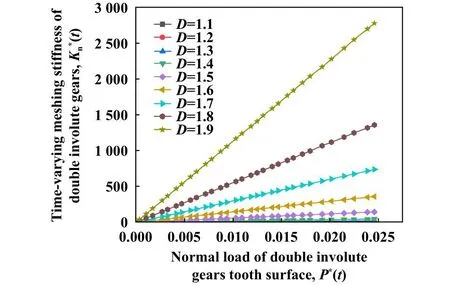
当al t时刻双渐开线齿轮真实接触面积与齿面法向载荷关系的无量纲形式为 根据式(13)和(16),得齿面上单个微凸体的接触刚度为 通过式(8)、式(14)和式(22)可推导t时刻接触线li(t)上第j对等效圆柱体真实接触面积与接触刚度关系为 双渐开线齿轮副基本参数列于表1中. 表1 齿轮主要参数Table 1 Main parameters of gears 假设双渐开线齿轮接触线li(t)上第j对等效圆柱体受 法 向 载 荷=1 kN,=80 mm,E=150 GPa,=60 mm,可变,图4所示为关系曲线图.由图4可知:的数值始终在大于0小于1的范围中,这是因为给定的两圆柱体接触并非无限区域接触,所以一对圆柱体表面接触的微凸体个数小于M-B分形理论中模型接触的微凸体个数;随着的增加而增加.此结论与文献[20]结果相符,所以选取合理. Fig.4 relational graph图4 关系曲线图 Fig.5 Surface contact coefficient distribution of double involute gears 图5 双渐开线齿轮表面接触系数分布 在分形模型中,假设Ra=1.6 μm,根据文献[23]中所述,确定分形维数D=1.51,粗糙度幅值G=10−6,通过式(17)~(21)可求出在一定齿面法向载荷下双渐开线齿轮在t时刻每段接触线上真实接触面积,再代入式(23)与(24)中,得到t时刻下的齿轮啮合刚度. 使用Matlab软件仿真,双渐开线齿轮有限元网格划分如图6所示,为避免较高的计算资源要求,考虑齿轮端面重合度接近于3,采用5齿啮合模型.通过对主动轮施加转矩,固定从动轮的方式,得到主动轮转角变形量Δθ,从而求出齿轮扭转啮合刚度KT(t),齿轮啮合刚度可以通过扭转啮合刚度与啮合刚度之间的转换表达式求出[24]. Fig.6 Schematic diagram of double involutegear finite element meshing图6 双渐开线齿轮有限元网格划分示意图 齿轮扭转啮合刚度KT(t)为 通过仿真,得到有限元仿真数据列于表2中. 表2 双渐开线齿轮有限元仿真数据Table 2 Finite element simulation data 同时对同参数普通渐开线斜齿轮进行仿真,并采用ISO 6336-1:2006 (E)[25-26]对其求解,其计算公式如下: 式中:z1为主动轮齿数,z2为从动齿轮齿数. 图7所示为双渐开线齿轮与同参数普通渐开线斜齿轮在分形模型与有限元模型和ISO 6336-1:2006 (E)方法下的时变啮合刚度计算结果对比图.由图7可知,单齿啮合刚度均随啮合时间的增加而先增大后减小;在相同啮合时间条件下,分形模型计算出的齿轮啮合刚度小于有限元模型中所求数值,但为同一数量级,这是由于在有限元模型齿面中为理想光滑曲面,未考虑齿面粗糙度,齿面接触面积较大,使得在相同载荷作用下,齿面变形量较小;在相同计算模型下,双渐开线齿轮比普通渐开线斜齿轮的单齿啮合刚度要略大一点;分形模型中普通渐开线斜齿轮的单齿啮合刚度最大值为2.915 62×109N/m,有限元模型中普通渐开线斜齿轮的单齿啮合刚度最大值为3.829 95×109N/m,而采用ISO 6336-1:2006 (E)计算出的普通渐开线斜齿轮的单齿啮合刚度最大值为3.215 33×109,本文中所提出的分形模型计算结果与ISO计算结果更为接近,之间的误差在9.4%以内.通过以上比较,表明所建分形模型合理可靠. Fig.7 Results comparison chart图7 结果对比图 为了便于观察分形模型中双渐开线齿轮时变啮合刚度变化趋势,通过6次多项式对分形模型单齿啮合刚度曲线进行拟合,双渐开线齿轮时变啮合刚度如图8所示. Fig.8 Time-varying meshing stiffness Kn(t) of double involute gears in fractal model 图8 分形模型中双渐开线齿轮时变啮合刚度,Kn(t) 改变不同参数数值(如摩擦系数、齿轮材料的特性参数、分形维数以及粗糙度幅值),探究双渐开线齿轮时变啮合刚度与各参数之间的相互关系与变化规律. 图9所示为ϕ=0.005,D=1.51,G=10−6时,摩擦系数μ与齿面法向载荷对双渐开线齿轮时变啮合刚度的影响.由图9可知,随着横坐标载荷增大,齿轮啮合刚度提高;同载荷条件下,随着摩擦系数μ增大,齿轮啮合刚度降低.由式(14)可知,摩擦系数μ增大,导致齿面上微凸体弹塑性变形的临界面积ac增大,即轮齿在啮合过程中弹性接触面积占比增大,所以使齿轮啮合刚度提高.从图9中还可以发现,摩擦系数μ的数值在(0.1~0.3)范围时,齿轮啮合刚度受摩擦系数μ的变化影响较小;当摩擦系数μ的数值在(0.3~0.9)范围时,齿轮啮合刚度受摩擦系数μ的变化影响较大.这一分析结论与文献[9]中的模型仿真结果吻合,同时也验证了本模型的正确性. 图10所示为μ=0.02,D=1.51,G=10−6时,齿轮材料的特性参数ϕ与齿面法向载荷对双渐开线齿轮时变啮合刚度的影响.由图10可知,同载荷条件下,随着齿轮材料的特性参数ϕ增加,啮合刚度提高.因此,齿轮材料的特性参数ϕ与啮合刚度为正比例关系.由式(14)可知,齿轮材料的特性参数ϕ增加,即齿轮材料的屈服极限σy增加,使轮齿在啮合过程中弹性接触面积占比增大,所以齿轮啮合刚度提高. Fig.9 The relationship between friction factor μ and meshing stiffness图9 摩擦系数μ与啮合刚度的关系 Fig.10 The relationship between the characteristic parameters of the gear material ϕ and the meshing stiffness图10 齿轮材料的特性参数ϕ与啮合刚度的关系 Fig.11 The relationship between fractal dimension D and meshing stiffness图11 分形维数D与啮合刚度的关系 图11所示为μ=0.02,ϕ=0.005,G=10−6时,分形维数D与齿面法向载荷对双渐开线齿轮时变啮合刚度的影响.由图11可知,同载荷条件下,双渐开线齿轮啮合刚度随分形维数D的增加而提高.这是由于分形维数D的增加导致齿面粗糙度降低,齿面变得较为光滑,接触面积增加,啮合刚度提高.当分形维数D<1.4时,D的取值对齿轮啮合刚度影响较小. 图12所示为μ=0.02,ϕ=0.005,D分别取1.5、1.6和1.7时,粗糙度幅值G与齿面法向载荷对双渐开线齿轮时变啮合刚度的影响.由图12可知,同载荷条件下,双渐开线齿轮啮合刚度随粗糙度幅值G的增加而降低.通过对比图12(a~c)可以发现,随着分形维数D越大,双渐开线齿轮啮合刚度随粗糙度幅值G变化的幅度越明显. 考虑齿面微观形貌与摩擦,结合一对反向阶梯圆锥滚子接触模型,将每一啮合时刻下齿轮接触线“分段”,把每段接触线上的接触等效为m对圆柱体接触,基于M-B分形理论与赫兹接触理论,建立了包含齿面摩擦系数μ、表面接触系数、齿面分形维度D、粗糙度幅值G和齿轮材料特性参数ϕ等因素的双渐开线齿轮时变啮合刚度分形模型. Fig.12 The relationship between roughness amplitude G and meshing stiffness图12 粗糙度幅值G与啮合刚度的关系 通过齿轮啮合刚度分形模型、有限元模型与ISO 6336-1:2006 (E)结果对比分析,验证了所建分形模型的合理性. 通过分析齿面形貌参数与双渐开线齿轮时变啮合刚度关系,得出以下结论: a.摩擦系数μ的增加,会导致双渐开线齿轮轮齿啮合刚度降低,当摩擦系数小于0.3之后对啮合刚度影响不大. b.齿轮材料特性参数ϕ的增加,使轮齿在啮合过程中弹性接触面积占比增大,提高了双渐开线齿轮啮合刚度. c.分形维数D增加、粗糙度幅值G减小,即齿轮齿面粗糙度Ra减小,均会使双渐开线齿轮啮合刚度提高,但分形维数D影响更大.1.3 考虑粗糙度的啮合刚度
2 分形模型与有限元模型对比及验证

2.1 双渐开线齿轮表面接触系数合理性分析
2.2 分形模型与ISO标准、有限元模型仿真对比

3 双渐开线齿轮分形模型影响因素分析
3.1 摩擦系数μ与双渐开线齿轮啮合刚度的关系
3.2 齿轮材料特性与双渐开线齿轮啮合刚度的关系
3.3 分形维数D与双渐开线齿轮啮合刚度的关系
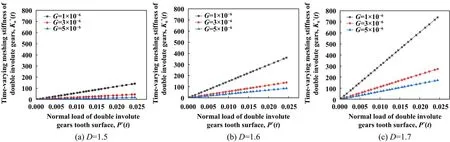
3.4 粗糙度幅值G与双渐开线齿轮啮合刚度的关系
4 结论