灰色系统理论在中国外贸出口额趋势预测中的应用

摘 要:对受复杂不确定因素影响的出口额进行预测对一国经济而言至关重要。文章通过灰色系统理论建立GM(1,1)模型,对数据量少且受未知复杂多因子影响的贸易出口额进行预测。结果表明,短期而言,模型预测效果良好,中国未来将依旧维持较高的出口额,政府与相关企业应积极参与外贸活动,创建稳态的外贸环境,从而促进经济良好发展。
关键词:灰色系统理论;外贸出口;趋势预测
中图分类号:F752.62 文献标识码:A 文章编号:1005-6432(2023)10-0009-05
DOI:10.13939/j.cnki.zgsc.2023.10.009
1 引言
作为拉动GDP的三驾马车之一,对外出口在一个国家的经济体系中占据重要的位置。数据显示,2000—2013年我国货物出口贸易总额提升了19604亿美元,一跃成为世界第一大货物出口国,但出口额高增长背后是我国出口产品的竞争力在全球仅为29位[1]。与此同时,近年来随着新型冠状病毒在全球的肆虐,无论是市场需求减退还是世界供应链危机加剧,都严重地冲击着世界的外贸体系。在这种情况下,2020年我国的外贸出口在新冠疫情显著的负面影响下也遭受打击[2]。但2021年随着国内疫情得到控制,各地企业全面复工,我国出口实现了新的增长。根据中国国家统计局数据计算,2021年我国外贸出口额同比增长21.23%,逆势上扬,极大促进了我国GDP的增长。因此面对外贸出口额所呈现出的复杂且重要的属性,无论是为了给亟待转型的我国外贸出口领域做出研究贡献,还是给相关企业制定相应策略与政府制定合理的利出口宏观政策提供建议,抓住外贸机遇促进我国经济进一步良性发展,对叠加疫情影响的出口数据趋势进行预测有着十分重要的意义。
对受复杂变量影响的数据的预测一直是数据研究的重点,各类方法繁多,但可大致分为三类。第一类是基于时间序列理论的统计学方法,其核心是将复杂的变量内化入原始数据内部,通过对数据的处理进行带有线性状态预测分析。如许立平等学者以ARIMA模型对带有波动性的黄金价格进行分析[3]。第二类是基于人工智能等网络技术,通过建立神经网络模型等方式进行的趋势预测分析。如李朋林等学者通过采用BP神经网络建立非线性模型对煤炭价格做出了精确的预测[4]。第三类是将上述两种或其他各类方法相结合,通过建立多个模型对预测结果进行优化。如陈蔚采用通过BP神经网络模型对基于ARIMA模型预测的出口额当中的非线性部分进行了补正,从而使模型呈现出更好的预测效力[5]。但无论是线性预测还是非线性预测抑或组合模型,具备良好预测效力的前提都是基于大量的历史数据,但对于包含较少数据的序列都难以使得预测模型对原始数据进行较好的拟合,从而很大程度上影响了模型的预测效力。
我国学者邓聚龙提出的灰色系统理论在针对少量样本且部分信息已知,部分信息未知的数据中呈现出较好的预测效果[6]。其中GM(1,1)模型作为灰色系统理论的核心,通过对经由累加处理的原始序列所构成的新序列建立相应的微分方程模型,最终可以实现对系统短期趋势的预测。由于我国出口额数据序列受包括疫情在内的原材料、价格、企业激励制度等多种不确定的复杂变量影响,且为了提高数据具备参考价值的自相关性,导致其所能选取的数据集中于近几年,数据量较少,其属于灰色系统理论适用的数据范畴,因此文章使用GM(1,1)模型对我国未来出口额进行趋势预测,并验证其结果的精确程度,从而针对预测结果对模型在实际应用中的优劣进行讨论,并从宏观和微观层面上分别对我国政府与外贸企业提出相应对策与建议。
2 灰色GM(1,1)预测模型
GM(1,1)模型是通过对信息不完全且数量较少的灰色系统内的样本序列利用累加生成法生成一个减少随机性干扰的新序列,通过建立并求解微分方程,从而描述其变化趋势的模型。
2.1 建模的条件
应选取在信息不完备的灰色系统中具有非负性的单调光滑的离散数据作为建模的数据[7]。设原始序列X(0)=(X(0)(1), X(0)(2), X(0)(3), …, X(0)(n)),则可求得序列的级比λ(k),即:
λ(k)=X(0)(k-1)X(0)(k),k=2, 3, …, n(1)
此时若原序列級比全部落在覆盖区间内,即λ(k)∈(e-2n+1, e2n+1),则说明原序列可进行GM(1,1)建模,并进行灰色预测。
2.2 序列的处理
由原序列X(0)做1-AGO序列X(1),即:
X(1)=(X(1)(1), X(1)(2), X(1)(3), …, X(1)(n))(2)
式中,X(1)(k)=∑ki=0X(0)(i), k=1, 2, …, n
2.3 邻值处理
由序列X(1)做邻值生成序列Z(1),即:
Z(1)=(Z(1)(1), Z(1)(2), Z(1)(3), …, Z(1)(n))(3)
式中,Z(1)(k)=12(X(1)(k)+X(1)(k-1)), k=2, 3, …, n
2.4 求解模型的微分方程
定义GM(1,1)的灰色微分方程为:
X(0)(k)+aZ(1)(k)=b(4)
将k=2,3,…,n代入式(4)可得并构造矩阵向量Y和B可得:
Y=X(0)(2)X(0)(3)…X(0)(n); B=-Z(1)(2)1-Z(1)(3)1……-Z(1)(n)1
此时可运用最小二乘法求出:
a︿=(a, b)T=(BTB)-1BTY(5)
基于式(4)中的GM(1,1)灰色微分方程,若将时刻k=2,3,…,n视作连续变量t, 则可得其对应的白化型微分方程:
dX(1)(t)dt+aX(1)(t)=b(6)
其解为:
X(1)(t)=(X(0)(1)-ba)e-a(t-1)+ba(7)
将式(8)中的时间变量t离散化后,可得GM(1,1)模型的时间响应序列,即:
X︿(1)(k+1)=((X(0)(1)-ba)e-ak+ba,k=1, 2, 3, …, n-1(8)
最后由序列 X︿(1)(k+1)累减还原得最终预测值为:
X︿(0)(k+1)=X︿(1)(k+1)-X︿(1)(k),k=1, 2, 3, …, n-1(9)
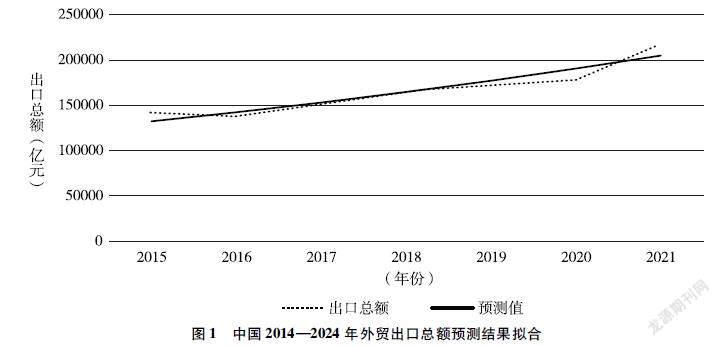
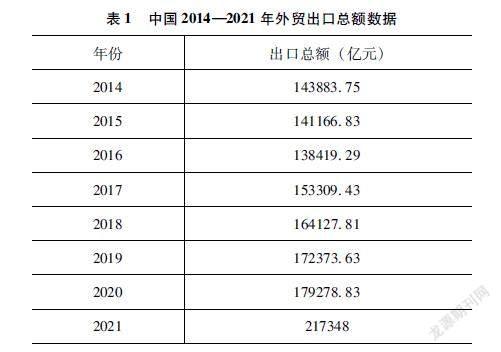
此过程中a为发展系数,且-2 2.5 模型的检验 2.5.1 平均绝对误差检验 文章用平均绝对误差百分比MAPE(mean absolute percentage error)作为模型残差检验的标准,模型的精度随着MAPE值与0的距离的减小而增大,当MAPE值大于100%时,则表示该预测模型为劣质模型。其公式为: MAPE=100%n∑ni=1At-FtAt(10) 式中,At为实际值,Ft为预测值。 2.5.2 后验比 C值检验 后验比C值用于模型精度等级检验,C值越小,模型精度越高,一般而言,C值小于0.35说明模型精度等级较好,C值小于0.65说明模型精确度基本合格[11],否则模型为劣质模型,其公式为: C= S21S20(11) 式中,S1为原始序列的标准差,S0为残差序列的标准差。 2.5.3 小误差概率检验 P=p{ε(k)-ε(k)<0.6745S0}(12) 3 基于GM(1,1)模型的中国外贸出口点额预测 3.1 数据来源 如表1所示,文章中的原始数据来自国家统计局,为使模型的预测结果更具备参考价值,文章选取近8年即2014—2021年的外贸出口总额数据进行原始序列的构建。3.2 预测结果 根据前文所述建模方法,通过Matlab工具输出数据可得中国2014—2024年外贸出口总额预测结果,如表2所示。 3.3 精度检验 在残差检验中,由表2中的绝对误差百分比相加取平均值,可以得到平均绝对百分比误差MPAE=3.4627%。平均误差在10%以内,预测精度较高。在模型检验中后验比C=0.3060<0.35,p=1.000>0.95。通过对已有的原始数据及预测数据的比较可做出预测结果的拟合图,如图1所示,两者的变化长趋势图像几乎完全重合,表明该模型拟合程度极高。综上所述,基于GM(1,1)模型的中国外贸出口额预测模型的预测效果极佳。 3.4 中国2022—2024年外贸出口额趋势预测 由表2预测数据可知,中国2024年外贸出口额将从2021年的217348亿元增长至2024年的254815.4058亿元,总体增长17%,平均每年增速可达4%以上,这意味着未来3年的出口额依旧维持持续正向增长趋势,而区别于2020—2021年出口额猛增的情况,2021年后我国外贸出口额年增速放缓。这一方面说明来自未知因子的影响在2021年后减弱,另一方面说明我国外贸出口额此时拥有相对稳定的增长趋势。 4 结论 4.1 模型评价 通过灰色系统理论所建立的GM(1,1)模型整体较为简单,对数据的需求量较少,适合中短期预测。文章根据其在我国外贸出口总额中趋势预测的应用对其适用性加以验证,并得出以下结论。 从理论角度看,文章基于中国外贸出口总额的统计数据和出口额预测的复杂及不确定性,通过其隶属于灰色系统的特性建立了中国外贸出口额的GM(1,1)灰色预测模型。通过对模型精度检验,中国外贸出口额GM(1,1)模型可以比较精确地预测未来几年的外贸出口额变化趋势,因此GM(1,1)模型在我国外贸出口额的短期预测上具有使用效力,具备一定参考价值。其中,不难发现预测模型在出口额的预测数据上呈现出较为稳定的每年7.5%左右的增长速度,这是由于GM(1,1)作为时间序列方法中的预测模型,其预测的依据全部来自前一期的原始数据,所以在變化趋势上会呈现出更加平稳的情况,因此在进行GM(1,1)短期预测时,构造原始序列的数据选取上应尽量选择靠近预测年份的数据,否则由于时间尺度太大,预测结果将很难具备参考价值。 从现实角度看,模型的结果反映了我国未来4年的外贸出口额将依旧维持较高的增长速度,这在问题研究的实际层面避开了需要对我国外贸出口额所受的不确定复杂因子的影响的分析来进行预测,而直接从预测结果本身反过来论证了我国高出口额背后是各类具备自相关的因素不断影响的结果,这一方面是对我国外贸出口行业中企业以及国家政策的肯定,另一方面也表明了我国企业与政策制定者需要继续通过调整企业经营策略与国家政策,从而共同维持与促进外贸出口额的相对稳定的总体增长趋势,推动我国经济发展。 4.2 建议 长期以来,我国出口产品一直存在数量评价显著好于质量评价的情况,这在客观上使我国面临在国际市场锁定低端产品加工生产的角色的情况[12]。因此,为了给我国政策制定者制定相关政策以及相关企业调整相关经营策略提供一些帮助,文章基于GM(1,1)模型的预测结果提出如下几方面建议。 4.2.1 微观层面 (1)企业应积极进行出口相关产品生产,为技术创新积累资本。高外贸出口额背后代表的是旺盛的市场需求,因此,在极度繁荣的出口需求下,无论是大型企业还是中小微企业都可以获得较好的收入,此时高额的技术研发费用带来的风险将相对降低,因此企业尤其是传统制造业应当利用短期优渥的出口环境积累技术研发的资金,并加大研发投入,从而通过技术型产品在国际市场上获得更多的竞争优势。 (2)龙头企业发挥作用,促进高技术产业集群。高外贸出口额数据带来的高利润可能集中在少数大型出口企业中,因此为了避免小企业因希望赶上短期内出口高增长的风头盲目开工而导致我国总体出口产品的产能过剩,进而导致各类企业只能通过压低产品价格以获得高份额的市场地位,使得我国外贸企业陷入恶性竞争,龙头企业不应以大资金维持低价格高数量的生产,而应该通过提高工资水平等方式吸引人才,从而提高企业调查与研发能力,向技术型企业发展,以此吸引如科研院所等相关行业配套机构在企业周边形成产业集群,通过产业集群的正外部性,吸引更多的机构与人才,从而使得我国外贸出口行业进入良性循环。 4.2.2 宏观层面 (1)打造可持续发展的绿色经济。我国能维持较高的出口额与我国的经济发展水平是密不可分的。大量的劳动力与产业集聚为制造业生产物美价廉的出口产品提供了优势。预测数据显示,我国外来出口额将继续维持高增长高数值,这对我国的经济显然有促进作用,但政策层面也应该注意到,大量的制造业工厂将对我国的社会环境产生负担,因此政府应制定政策引导企业走可持续的经营道路,与企业配合打造绿色经济。 (2)优化资金分配方式,减小地区间发展不平衡。高出口额的背后一定程度上也反映了我国沿海地区和中西部地区发展的不平衡。由于出口额的不断增长,越来越多的资金流入东部沿海的出口大省,这将使我国产业资本集中于东部沿海地区,导致中西部地区缺乏研发资金,有可能因此陷入低收入陷阱,加大地区间发展的不平衡。因此,在出口额快速增长带来的高GDP增速背后,政策层面也应该充分意识到其对我国整体经济结构的影响,国家政策制定者可利用高出口额积累的资金,通过加大对基础设施的资金投入力度,如建设5G网络基站等方式降低我国中西部与沿海城市的沟通与运输成本。另外,通过优化税制等财政制度的方式致力于打造中西部特色支柱产业,从而减小地区间发展的不平衡,进一步完善我国经济结构。 4.3 展望 对外贸出口额的预测作为极为重要的研究内容,虽然经由灰色理论建立的GM(1,1)模型在文章中呈现出较好的预测效果,但在实际的应用中依旧有重大缺陷和优化空间。其一,GM(1,1)模型在数据选取上要求有明显指数型变化的数据,且只适用于中短期预测,在面对长期存在稳定非自相关的数据时预测效力明显不足。其二,作为时间序列模型,其预测结果只能说明该数据未来的走向,对更深层次的如因果关系等研究帮助较少。其三,在质量这一指标已成为评判出口产业转型升级重要标志的今天[13],单一的GM(1,1)模型的预测结果只显示出我国贸易额呈现高增长高数值的结果,但这一结果背后所展现的产业竞争力则无从所知,因此难以很好纳入质量这一变量的GM(1,1)模型可能会使得数据本身具有一定的迷惑性,从而影响对预测结果的理解,进而影响基于此的一系列行为。其四,对于受复杂因子影响的数据研究如果仅仅通过GM(1,1)模型本身是完全不够的,当国家政策、消费者预期,甚至是统计口径发生变化時都会导致预测值与实际值产生偏差,此时,单一的GM(1,1)模型的预测值将需要进行一定的修正才能具备更好的参考价值,因此,在对出口额的预测的实际应用中,可通过组合模型法叠加如马尔可夫链模型等非时间序列类模型对预测数据进行补充及修正。 参考文献: [1]刘伟,高理翔.技能人才激励政策、技能赋能与出口质量跃升——来自微观企业的证据[J].产业经济评论,2022(2):74-92. [2]杨逢珉,田洋洋.新冠肺炎疫情对我国出口贸易的影响[J].郑州航空工业管理学院学报,2022,40(1):11. [3]许立平,罗明志.基于ARIMA模型的黄金价格短期分析预测[J].财经科学,2011(1):26-34. [4]李朋林,梁露露.基于BP神经网络的煤炭价格影响因素及预测研究[J].数学的实践与认识,2015,45(17):113-126. [5]陈蔚.基于线性ARIMA与非线性BP神经网络组合模型的进出口贸易预测[J].统计与决策,2015(22):47-49. [6]邓聚龙.灰色控制系统[J].华中工学院学报,1982(3):11-20. [7]尹连生,白玉皎.GM(1,1)模型建模条件及模型改造[C].中国土地学会首届青年学术年会论文集,1992. [8]黄锦祥,鄢新余,熊伟,等.基于 GM(1,1)模型的宁化县油料产量和播种面积预测[J].亚热带水土保持,2014(2):12-14 [9]杨环.基于GM(1,1)模型对杭州市商品房房价的预测分析[J].南阳理工学院学报,2021,13(4):5. [10]张小允,李哲敏.基于GM(1,1)模型的中国小杂粮种植面积预测分析[J].中国农业资源与区划,2018,39(9):6. [11]胡立和,商勇,王欢芳.长江经济带技术创新效率评价及影响因素分析[J].湖南社会科学,2020(3):87-93. [12]姬潇涵,周定根,刘东华.环境规制与中国制造企业出口升级——基于节能低碳政策的准自然实验证据[J].生态经济,2022,38(4):137-144. [13]HUANG X,SONG X.Internet use and export upgrading:firm-evel evidence from China[J].Review of international economics,2019,27(4):1126-1147. [作者简介]郑东权(1999—),男,福建福州人,硕士研究生(商业硕士),研究方向:国际商务。

