子空间在线辨识算法原理及应用技术研究
赵 昂
(中国空空导弹研究院,河南 洛阳 471000)
0 引言
关于船舶模型的辨识开始于20世纪末。FOSSEN等[1]提出采用平行离线EKF算法来辨识船舶模型中对应的水动力参数,但是算法较为复杂。WANG等[2]提出了LS-SVM算法对船舶中的水动力参数进行辨识,该算法仅适用于离线辨识领域,并且要求的数据量较多。FUJIMORI等[3]提出在连续时间系统辨识领域中采用迭代学习控制来辨识某一连续时间状态空间模型。BERGAMASCO等[4]将基于预测器的子空间连续时间辨识算法应用到了四旋翼飞行器的参数辨识中,并取得了较好的辨识结果。
传统的船舶模型需要辨识的动力参数较多且较为复杂,因此很多学者将研究的重点转移到了对船舶黑箱模型的辨识中。MOREIRA等[5]采用递归神经网络模型得到了船舶输入和输出之间的非线性关系。MENDES等[6]将T-S模糊模型作为船舶预测模型,并将其应用于船舶广义预测控制中。
在过去的20年间,子空间辨识算法得到了学者们的广泛关注。NOEL等[7]介绍了在频域中采用子空间辨识算法得到系统模型。YAN等[8]提出采用递推子空间辨识算法辨识得到AUV模型。XIA等[9]推导出了船舶Hammerstein模型,并且将子空间辨识算法应用到了该模型的辨识中。
本文以动力定位船舶为研究对象,构建了船舶Hammerstein黑箱模型,并提出以该模型为基础的子空间辨识算法,接着提出采用Givens旋转矩阵对算法中复杂QR分解进行简化,最终形成了适应船舶黑箱模型辨识的在线子空间辨识算法。
1 船舶非线性Hammerstein辨识模型推导
1.1 船舶Hammerstein模型
根据经典的船舶三自由度非线性模型[10],选取作用在船上的横向、纵向作用力和转艏力矩(τ)作为辨识输入。最终的船舶模型结构图见图1。图中,υ1(k)、ω(k)和υ2(k)分别表示输入、输出测量误差和过程噪声。定义非线性反馈映射为ffd(·),于是船舶Hammestein模型便具有如下形式:

图1 带有非线性反馈的船舶Hammerstein模型

(1)
式中:x(k)∈R3为系统状态;p(k)∈R3为与推进器有关的参数;y(k)=[uvr]T∈R3为系统的测量输出;A、Bin、Bf、C、Din、Df为具有适当维数的系统矩阵。
测量的输入、输出数据可以表示为如下的结构形式(假设模型中遇到白噪声):
1.2 船舶非线性Hammerstein模型的优化
首先对Hammerstein模型进行适当的参数化。选取截断的Fourier级数对系统的非线性部分进行逼近。定义基函数如下:
L1=(xmin)max,L2=(xmin)max
式中:j=1,2,…,p。
非线性函数fin(·)可以展开成如下的形式:
fin(p)=W·η(p)
Wi=[Wiu1Wiu2Wiu3]∈R1×3(2N+1)
Wiuj=[ωuj0ωuj1…ωujN]∈R1×(2N+1)
η(p)=[ηT(p1)ηT(p2)ηT(p3)]T∈R3(2N+1)×1
式中:N为基函数的长度。
同样地,对非线性反馈函数ffd(y(k))可以展开成类似的形式,船舶模型转换为

(2)
B=[BinWBfM)],D=[DinWDfM)]
ε(k)=[ηT(p(k))σT(y(k))]T代表了系统的输入向量。
至此,得到带有非线性反馈Hammerstein船舶模型。
2 基于船舶Hammerstein模型的在线子空间辨识算法
采用Givens旋转矩阵来提高QR分解和奇异值分解的速度。算法推导前做出如下假设[11]:
(1)系统满足持续激励条件。
(2)噪声项d(k)、w1(k)、w2(k)不相关。
2.1 子空间MOESP辨识算法
MOESP辨识算法的思想在于首先得到系统的广义能观矩阵,根据该矩阵得到对应的系统矩阵。
首先忽略噪声项d(k)、w1(k)和w2(k),得到如下的输出数据方程:
Yp=ΓiXp+HiEp
(3)
式中:带有下角标p的矩阵为包含系统已知数据的Hankel矩阵; 矩阵Yp、Ep为输入输出Hankel矩阵;Xp为状态矩阵;Hi为下三角Toepliloz矩阵。
经典MOESP辨识算法的核心即通过辅助数据方程分解得到广义能观矩阵Γi的一致估计:
(4)
将式(4)和式(3)结合在一起可以得到:
这表明Γi的列空间在矩阵R22的列空间中。因此,通过对R22进行SVD分解就可得到Γi[12]:
(5)
于是可以得到广义能观矩阵Γi=R22。根据子空间辨识算法的定义,可以求出系统矩阵的相似变换矩阵(ATBTCTD)形式[11]。
2.2 变量含误差的子空间MOESP辨识算法
考虑系统受到d(k)、w1(k)、w2(k)误差的影响,于是式(3)将变为如下形式:
(6)
式中:W2f、Ωf分别包含了w2(k)、d(k);矩阵P为下三角矩阵。
(7)
从矩阵R22的SVD分解中得到广义能观矩阵Γi的一致估计,于是系统矩阵就可以通过上节中介绍的方法进行求解。
2.3 基于Givens旋转矩阵的QR分解优化策略
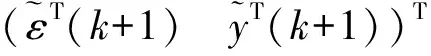
R(t+1)·QT(t+1)
(8)
接着,根据Givens旋转矩阵的特点,可以得到如下一系列Givens变换律:
R(t+1)QT(t+1)=R(t)G1G2…Gm·
Gi为Givens矩阵,且均为正交矩阵。于是括号中的矩阵乘积结果即形成了新的正交矩阵QT(t+1),最终可以得到:
R(t+1)=R(t)G1G2…Gm
即可以通过这样一系列的Givens变换进行更新。由于Givens矩阵的特殊结构,可以对该过程进行进一步的简化。假设当有新数据到来时,原矩阵R(t)具有如下的形式:
R(t)=[RΦnew data]=
最右边一列的数据为新测量得到的数据。首先,为了将Φ1置为0,定义:
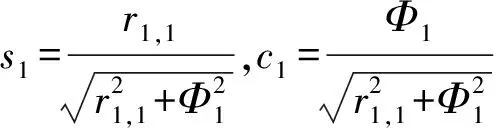
于是,对应元素(即第一列中的ri,1和最后一列中的元素Φi)可以通过如下的方式进行更新:
可以得到第一次递推之后的R(t)矩阵如下:

通过使用这种方法,可以直接处理原R矩阵中的对应列,降低了计算复杂度,提高了计算效率。
3 仿真验证
典型的动力定位系统方框图见图2。图中的虚线框部分为船舶模型辨识模块,并采用本文的算法对参数矩阵进行不断地在线调整。

图2 典型的动力定位系统框图
为了验证子空间辨识算法的有效性,对已经建模并修正过的实船数学模型进行20°Z形操舵实验,并将得到的输入输出数据用于子空间模型辨识算法[14]和经典船舶模型辨识算法中。对比仿真结果见图3~图4,可以看出子空间辨识算法的有效性。

图3 船舶速度辨识结果对比

图4 船舶速度辨识结果对比
假设系统的输入输出均受到白噪声的影响。算法中Fourier级数的项数取p=6。仿真中船舶初始位置为(0 m,0 m)~(+10 m,+8 m),分别为初始位置的正北和正东向。在定位到300 s的时刻,移动至(+5 m,+3 m),仿真结果见图5~图8。
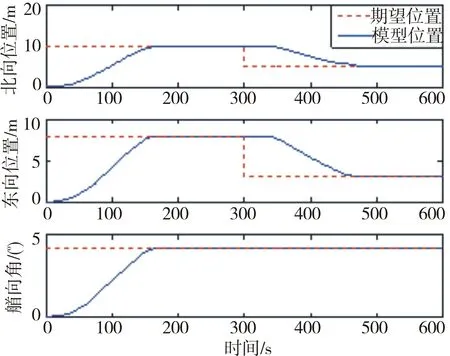
图5 位置和艏向跟踪情况
图5、图6表示船舶位置和艏向的跟踪情况和偏差,可以看出,基于船舶模型的预测控制算法能够满足动力定位系统的控制要求(位置偏差1 m以内,艏向误差1°以内)。从图7中可以看出,作用在船上的力和力矩均较为平滑。图8中数学模型的速度项输出(实线)和船舶仿真输出(虚线)结果基本重合,验证了辨识得到的船舶数学模型的正确性及本文在线子空间辨识算法的有效性。可以得出结论:基于子空间MOESP算法的辨识方法能够较为准确地辨识出船舶Hammerstein模型,实现了对船舶模型参数的实时调整,克服了传统船舶模型辨识算法只能对模型进行离线辨识的缺点,使得控制器的输入更为平滑。本文算法可以为紧急情况下的船位推算策略提供较为准确的模型依据,因此具有十分广阔的应用前景和工程意义。
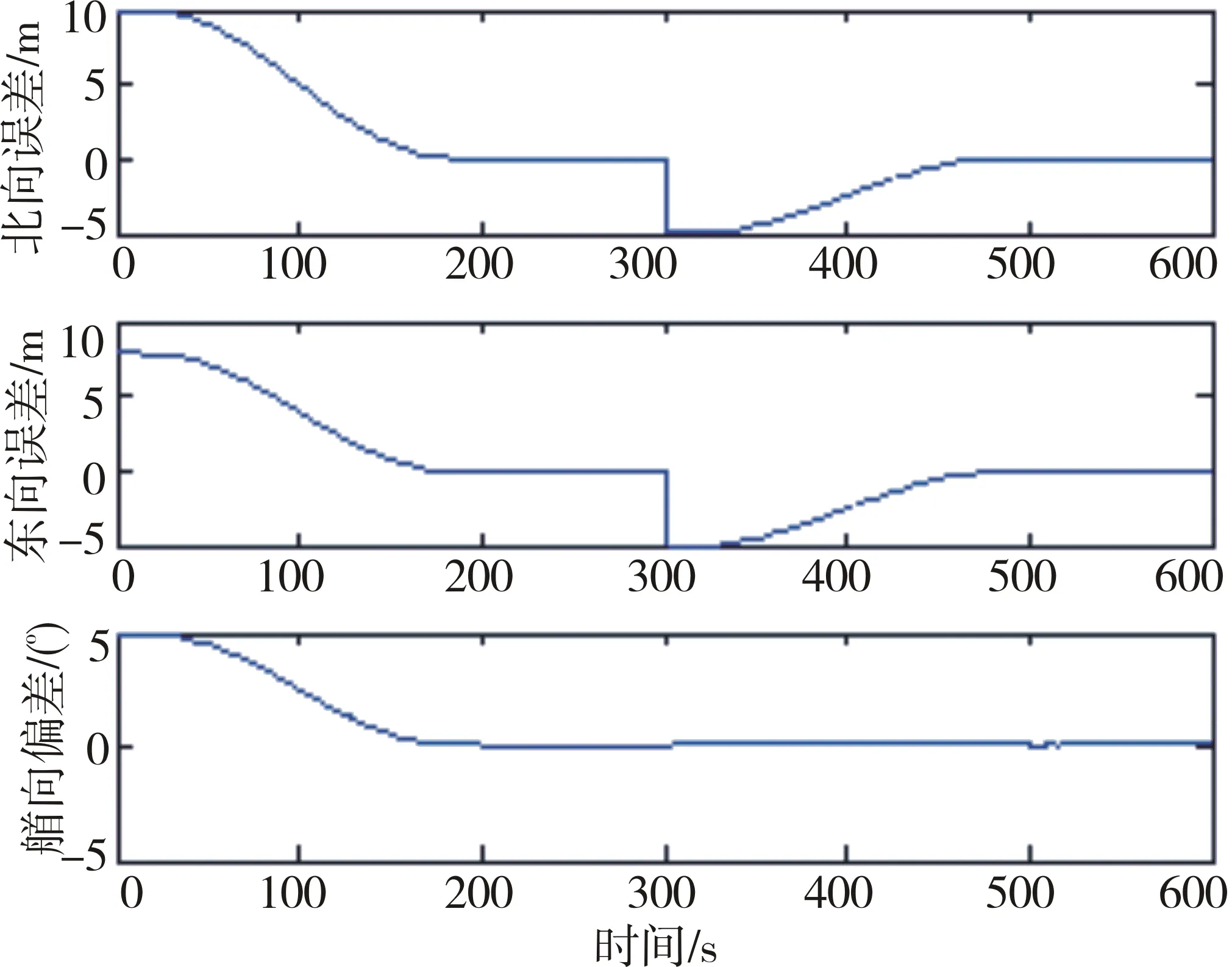
图6 跟踪误差

图7 船舶受到的纵向、横向、回转作用力和力矩
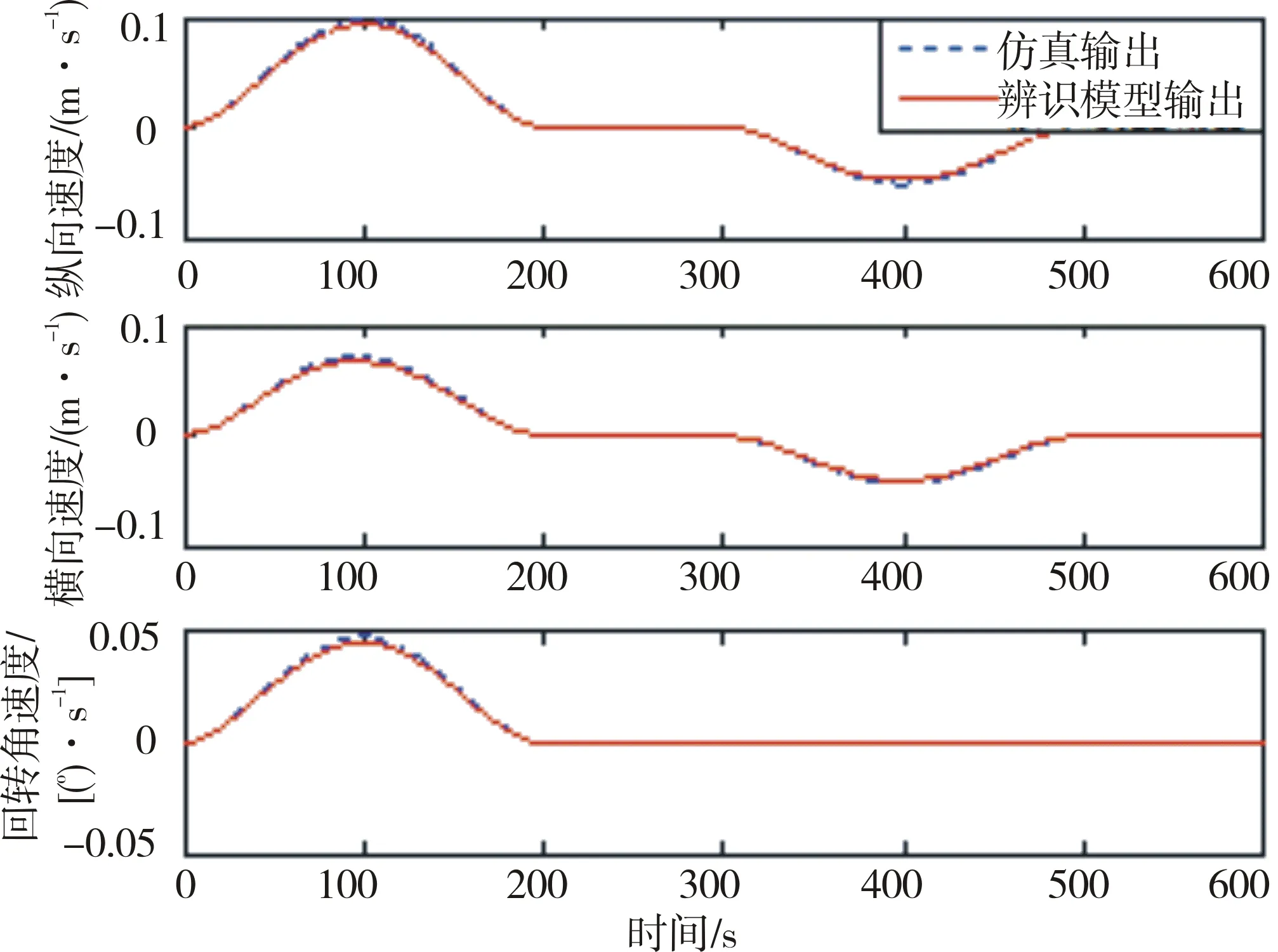
图8 辨识模型的速度项输出和仿真结果对比
4 结论
本论文推导了动力定位船舶非线性模型的Hammerstein结构形式,接着提出了基于MOESP算法的递推子空间辨识方法,使用简化的Givens旋转策略对子空间辨识中涉及到的复杂QR分解计算进行处理,降低了计算复杂度,实现了辨识算法的在线计算。最终将本文提出的子空间在线辨识算法应用到了船舶动力定位系统中,验证了基于子空间MOESP的在线辨识算法的有效性和适用性,为动力定位系统模型辨识提供了新思路。

