基于神经PID控制的随机分布系统的研究
屈 毅
(咸阳职业技术学院电子信息学院 陕西 咸阳 712000)
0 引 言
随机系统控制是控制领域中的一个研究方向,是用差分或微分方程定义的动态系统,系统变量的服从高斯统计特性,已形成较为完整的理论体系[1-5]。但是在许多工业生产过程中,系统变量的统计特性不满足高斯或者对称分布。Wang[6]提出了随机分布控制统计理论,建立系统的动静态数学模型,实现了概率密度函数统计控制策略,经过二十多年的研究与发展,初步构建了建模和控制理论,在建模方面,主要有线性B样条、平方根B样条、有理平方根B样条和有理B样条等模型理论[6-25];在控制算法方面,主要有线性系统控制、伪ARMAX系统控制、基于迭代学习控制、最小熵控制和自适应控制等算法[6-25]。
近年来,众多研究者在随机分布系统控制方面做出了一定的成效。例如,文献[8]提出了时滞系统的保性能控制方法;文献[9,15,23]研究了自适应容忍控制算法;文献[10]研究了基于神经的保性能控制策略;文献[11]提出了基于调和因子的容忍控制方法;文献[12,16,20,24]研究了时滞系统的故障检测与诊断控策略;文献[12,16,20,24]提出了时滞奇异系统的故障检测与诊断算法;文献[14]研究了基于PBF网络的容忍控制;文献[18-19,21]提出了基于学习因子的追踪控制方法;文献[22]研究了模糊随机分布系统的故障检测策略。随机分布系统虽已建立了一定的理论基础,但未知的领域还需继续研究与开拓。
对于非高斯连续随机分布系统追踪控制及控制中的干扰抑制问题,现有的文献鲜有报道。针对该问题,本文通过平方根B样条逼近建立系统输出概率密度函数模型(静态模型)和动态权值模型,接着设计神经PID控制器。控制器的目标是在满足系统规定的性能指标前提下,实现系统输出概率密度函数对目标概率密度函数的追踪。
1 建立系统静态模型
对于随机分布系统,如图1所示,在定义区间[a1,a2],概率密度函数τ(y,x(t))γ(y,u(k))是一致连续有界的,x(t)是系统的控制输入,y是系统的输出变量。则输出PDFγ(y,u(k))τ(y,x(t))的B样条平方根定义为:

图1 概率密度函数表达式示意图
(1)
式中:βi(y)(i=1,2,…,n)是已知的基函数;νi(x(t))(i=1,2,…,n)是与βi(y)对应Bi(y)的权值向量;δ(t)是系统静态模型的误差。
由式(1)可得:
(2)
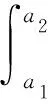
τ(y,x(t))=(υ0(t)β0(t)+υn(t)βn(t)+δ(t))2
(3)
式中:β0(t)=[β1(y),β2(y),…,βn-1(y)],υ0(t)=[v1(t),v2(t),…,vn-1(t)]T
定义δ(t)=ν0(y)δ0(t),δ0(t)为静态模型的补偿误差,则式(3)可表示为:
τ(y,x(t))=(β0(y)υ(t)+νn(t)βn(y))2
(4)
式中:υ(t)=υ0(t)+δ0(t)。
定义:

由式(4)可得:
νn(t)=h(ν(t))=
(5)
定义追踪的目标PDF为:
τg(t)=(β0(y)νg(t)+h(νg)βn(y))2
(6)
式中:τg(t)是目标PDF,νg是已知权值向量。随机分布系统控制的目的是调整输入x(t),使系统输出PDFτ(y,x(t))追踪目标PDFτg(t)。
定义随机分布系统输出PDF与目标PDF的误差为:
β0d(t)+[h(ν(t)-h(νg)]βn(y)
(7)
式中:d(t)=ν(t)-νg。

2 神经PID控制器的设计
随机分布系统神经PID控制是设计一个控制器,以H∞作为性能指标,使系统输出概率密度函数追踪目标概率密度函数,并使系统的鲁棒性和稳定性等得到满足。
2.1 神经PID控制器
采用含神经PID控制算法,其结构如图2和图3所示,在该算法中,用神经PID控制器调整权值线路,以实现在线的自适应控制和学习。

图2 随机分布系统神经PID控制器结构图

图3 三层神经网络PID结构
2.2 动态模型建立
随机分布系统输入和输出间关系转化为x(t)和权值ν(t)的关系,则x(t)和ν(t)的非线性动态模型为:
(8)

对于式(8),定义新的向量为:
(9)
则式(8)转化为:
(10)
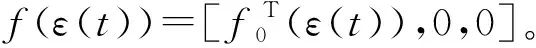

随机分布系统控制转化为系统稳定性问题,则神经PID控制器定义为:
(11)
对于ν(t),由李雅普诺夫条件可得:

H∞范数的定义:扰动w(t)到系统输出σ(t)的H∞范数定义为:

为了便于后边的证明,引入以下两个引理。
引理1给定适当维数矩阵D、E,对称矩阵Y,以及矩阵F(FTF≤I),要使下式成立:
Y+DFE+ETFTDT<0
当且仅当存在一个标量ε>0,使得:
Y+εDDT+ε-1ETE<0
引理2对于任意向量x,y和一个正定标量π,则下列矩阵不等式成立
2xTy≤πxTx+π-1yTy
2.3 设计方法
下面通过两个定理给出控制器设计的方法。

(12)

证明:定义Lyapunov-Krasovskii函数为:

(13)
对式(13)求导,并应用引理1,可得:
2εT(t)QTF0f(ε(t))+2xT(t)PTW0w(t)+
2εT(t)QTW0w(t)+λ-1εT(t)QTHHTQε(t)+
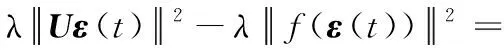
式中:

由H∞可得:



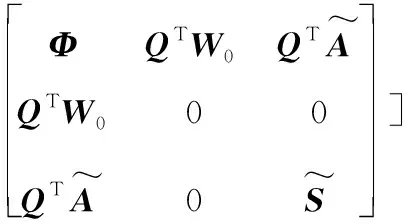



式中:
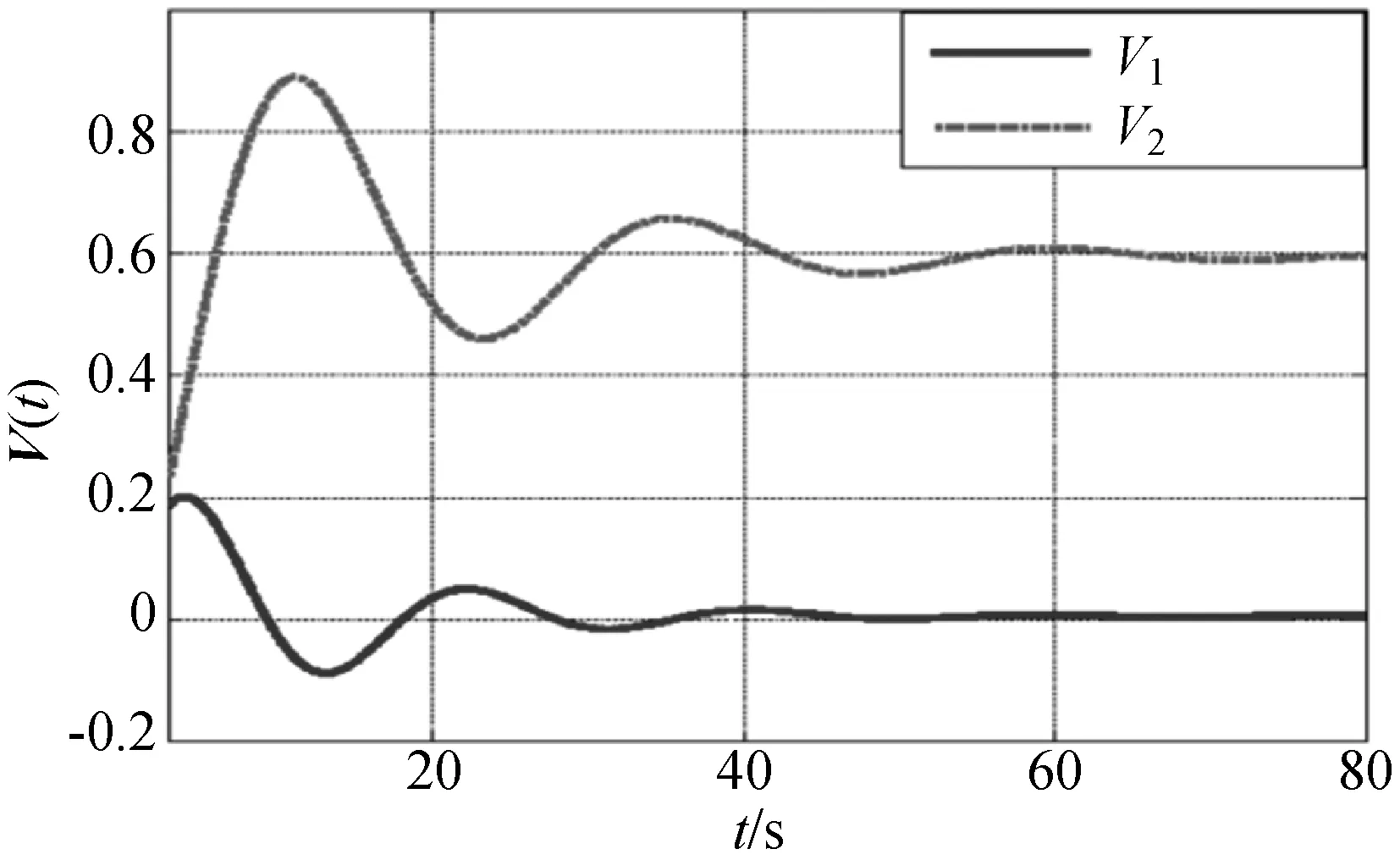
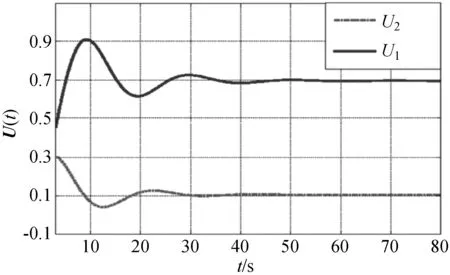
则有Ξ1 由矩阵不等式理论可知: 则进一步可得出: 应用初始条件V(0,0)=0,可得: 由于V(x(t),t)>0,可得: 证明完毕。 采用状态反馈H∞控制,将控制器x(t)=κε(t)代入式(10),则得到随机分布闭环系统,表示为: (14) 定理2为神经PID控制问题提供了一个解决方案。 定理2已知参数λ,ξi(i=1,2)和矩阵U,假设存在矩阵P=Q-T,Σ,Si>0,(i=1,2,…,n)和标量γ>0,使下列线性矩阵不等式(15)有可行解,则式(14)表示的闭环系统是稳定的。 (15) (16) 证明:在定理1的基础上,利用Lyapunov-Krasovskii函数式(13)可得: 2εT(t)QTFf(ε(t))+2εT(t)QTW0w(t)+ γ-1σT(t)σ(t)-γwT(t)w(t)= θ1εT(t)Pε(t) 定义: 由Υ>0,可得: (17) 在式(17)两边分别左乘和右乘diag{Q-T,I,I,Q-T,I,I,I},diag{Q-1,I,I,Q-1,I,I,I},可得 应用参数式(16)的定义,可得式(15)成立。进而可知: 则式(14)渐近稳定。 通过定理2,H∞优化PID控制器的设计转化为对解线性矩阵不等式(LMI)的求解。 为了验证提出算法的有效性,下面对提出的算法在MATLAB中的Simulink Library环境下仿真验证,在仿真中三个PID参数值[kp,ki,kd]调整状态向量和控制向量[V(t),U(t)]。 在数字仿真中,随机分布系统输出概率密度函数可使用平方根B样条逼近,表示为: 式(4)中n=3,y∈[0,1.6i],i=1,2,3。 采用平方根B样条逼近建立系统输出概率密度函数模型,因隐含条件存在,3个权值之中只有两个权值独立,假设v1、v2相互独立。 系统(10)的参数及其他参数取值如下: F=diag{0.6,0.6},B0=diag{0.5,0.5} Bτi=diag{-0.5,-0.5},W0=diag{-0.5,-0.5} U0=diag{0.3,0.5} λ=3,μ1=μ2=1,γ=0.6 则计算可得: 系统输出概率密度函数权值变化的响应如图4所示,系统控制输入变化的响应如图5所示。从图4和图5仿真的结果分析可得系统实际输出概率密度函数追踪逼近目标概率密度函数,可获得满意的扰动衰减性能,并可确保系统渐近稳定。 图4 系统静态模型对权值变化的响应 图5 系统控制输入变化的响应 本论文研究了随机分布系统的神经PID控制算法的问题。通过B样条平方根逼近建立系统的静态模型,提出神经PID控制器的结构,建立系统的动态模型,引入H∞范数,提出了系统稳定性的条件,在随机分布闭环系统的基础上,通过线性矩阵不等式的求解给出了在满足干扰抑制的条件下,神经PID控制器的设计方法。最后,计算机仿真验证表明:所提出的算法可满足追踪控制性能,并可抑制追踪控制中的干扰。


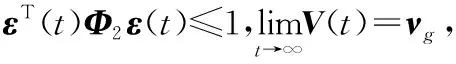

3 计算机仿真
4 结 语

