单位圆盘上几种Toeplitz算子的数值域①

丁宣浩， 王章逸， 邵长慧， 李永宁

1.重庆工商大学 数学与统计学院，重庆 400067；2.经济社会应用统计重庆市重点实验室，重庆 400067

设T为Hilbert空间上的有界线性算子.记T的谱为σ(T).记集合S的凸包为convS.则算子T的数值域定义为集合

W(T)={〈Tf,f〉:f∈H,‖f‖=1}

与算子的谱类似,算子的数值域是复平面中的子集,并且可以反映出算子的一些代数性质.例如,T是自伴算子当且仅当W(T)⊂R,T是半正定的当且仅当W(T)⊂[0,∞)．

由于本文的需要,这里列举一些算子数值域的简单性质,其证明可参见文献[1-2].更多关于算子数值域的知识,我们推荐文献[2-3]．

引理1[1]算子T的数值域W(T)具有下述性质:

(i)W(T)是凸集;

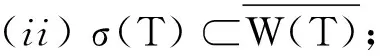
(iii) 对任意的α,β∈C,W(αT+βI)=W(T)+β;

(v) 对任何的酉算子U,W(U*TU)=W(T);

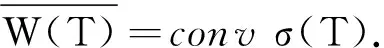
设H1,H2为Hilbert空间,记F为H1⊕H2上的由下述分块形式给出的线性算子

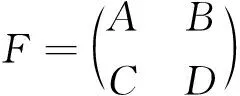
这里A和D分别表示H1和H2上的线性算子,B为从H2到H1上的线性算子,C为从H1到H2上的线性算子．

2×2分块算子的二次数值域的概念是由文献[4]引入的,定义为集合

下述关于F的二次数值域的性质在我们主要结果的证明中很有用,故我们引用如下(引理2),而且,为了读者阅读方便,这里我们用更直接的方法证明了第一条性质,这与文献[5]中的证明方法不同．

引理2[5]H1⊕H2上的线性算子F的二次数值域W(F)具有如下性质:

(i)W2(F)⊂W(F);

(ii)σ(F)⊂W2(F);

(iv) 若dimH2>1,则W(F)⊂W2(F); 若dimH1>1,则W(D)⊂W2(F)．

证(i) 对于任意给定的x∈H1,y∈H2且‖x‖=‖y‖=1,定义Fxy为

则Fxy是从C2到C2的有界线性算子.而且,易知

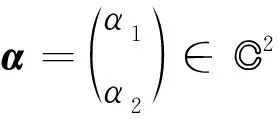
则有

令f=α1x+α2y.因为x⊥y,

由于

故可得

从而推出W(Fxy)⊂W(F).因为有限维线性空间上的有界线性算子的数值域是紧集,所以

由上述事实和引理1,可得

因此,对任意的x∈H1,y∈H2,则有

(1)

从而性质(i)得证．

对于有界线性算子,由引理2中的(i)和(ii)可知在线性算子的谱刻画方面,二次数值域能提供比数值域更精确的信息．

设D是复平面C上的单位开圆盘,H2是单位开圆盘上经典的Hardy空间,L2=L2(T)为单位圆周T={z∈C: |z|=1}上的Lebesgue空间.设H∞为D上的有界解析函数所构成的空间.根据Fatou定理和调和延拓定理[6],我们通常将H2与L2(T)中由解析函数构成的闭子空间等同起来．

设P为从L2到H2上的正交投影算子.对任意的φ∈L∞,Hardy空间上的Toeplitz算子Tφ定义为

Tφx=Pu(φx)x∈H2

Hφx=(I-P)(φx)x∈H2

Hardy空间的正交补空间(H2)⊥上的对偶Toeplitz算子Sφ定义为

Sφy=(I-P)(φy)y∈(H2)⊥

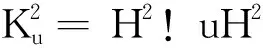
容易验证

记Mφ为L2上的乘法算子,则在L2=H2⊕(H2)⊥下,由简单计算可得

(2)

(3)

1 Hardy-Toeplitz算子的数值域和二次数值域

在本节,我们研究用Toeplitz算子的符号来刻画Hardy空间上Toeplitz算子的数值域和二次数值域.由Hardy空间上Toeplitz算子的代数性质[11]可知,所有的Hardy-Toeplitz算子均是凸算子.文献[12]应用算子的谱完全刻画了任意一个Hardy-Toeplitz算子的数值域．

引理3[13](i)若φ∈L∞为非常值函数且Tφ是正规算子,则σ(Tφ)是一条连接a和b的闭直线段[a,b],并且W(Tφ)是对应的开直线段(a,b);

(ii) 若φ∈L∞为非常值的函数且Tφ不是正规算子,则W(Tφ)=(convσ(Tφ))°,其中E°表示集合E的内部;

(iii) 若φ∈H∞,则W(Tφ)=convφ(D)．

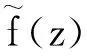
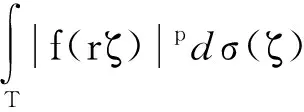
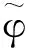
定理2设φ∈L∞,Mφ是L2上的乘法算子,则

(4)

证一方面,∀z∈D,

φ(z)=〈Mφkz,kz〉∈W(Mφ)

则有

φ(D)⊂W(Mφ)

从而

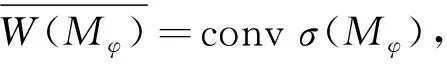
从而可得

将以上两方面结合起来,则结论得证．

下述定理3用符号的值域刻画了有界符号的Hardy-Toeplitz算子的数值域．

定理3设φ∈L∞,则

证一方面,由于Mφ在空间分解L2=H2⊕(H2)⊥下的表示为

以及dim(H2)⊥>1,根据引理2,可得

W(Tφ)⊂W2(Mφ)⊂W(Mφ)

另一方面,对任意的z∈D,因为

φ(z)=〈Tφkz,kz〉=〈φkz,kz〉∈W(Tφ)

则有φ(D)⊂W(Tφ).从而

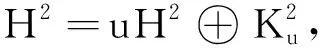
(5)

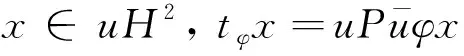
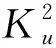
在Tφ的上述表示((5)式)下,Tφ的二次数值域为

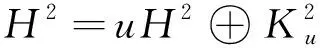
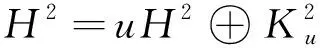
W2(Tφ)=W(Tφ)

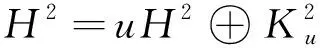
W(tφ)⊂W2(Tφ)⊂W(Tφ)

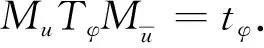
W(tφ)=W(Tφ)

从而

W2(Tφ)=W(Tφ)

2 Bergman-Toeplitz算子的数值域

在本节中,我们给出了Bergman空间上Toeplitz算子的数值域的刻画．

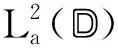
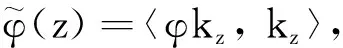
文献[19]研究了Bergman空间上调和符号的Toeplitz算子的性质,给出了有界调和符号的Bergman-Toeplitz算子的数值域刻画,并应用符号的值域刻画了解析符号的Bergman-Toeplitz算子的数值域,这里我们引用如下(引理4).由于调和符号的Bergman-Toeplitz算子和Hardy-Toeplitz算子的性质相似[20],本节我们运用符号的值域给出有界解析符号的Bergman-Toeplitz算子的数值域的类似刻画．

引理4[19](i) 设φ是单位圆盘D上的非常值的有界调和函数,且Tφ为正规算子,则存在常数a,b使得σ(Tφ)=[a,b]且W(Tφ)=(a,b);

(ii) 设φ是单位圆盘D上的非常值有界调和函数,且Tφ不是正规算子,则W(Tφ)是一个开凸集;

(iii) 若φ∈H∞,则W(Tφ)=convφ(D)．

类似定理2,应用Berezin变换可证得下述结论:

引理5设φ∈L∞(D),Mφ是L2(D)上的乘法算子,则

下面,我们给出有界调和符号的Bergman-Toeplitz算子的数值域的不同形式的刻画:

定理5设φ是单位圆盘D上的有界调和函数,则

W(Tφ)=convφ(D)

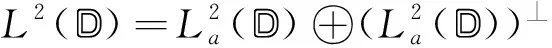
W(Tφ)⊂W2(Mφ)⊂W(Mφ)

(6)

对任意的z∈D,因为

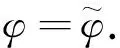
φ(D)⊂W(Tφ)

因此

根据引理5及关系式(6),可得

因为紧集的凸包仍是紧集,开集的凸包仍是开集,以及开凸集等于其闭包的内部,根据引理4,故可得

W(Tφ)=convφ(D)

3 对偶截断Toeplitz算子的数值域和二次数值域

(7)

其中Sφ为定义在(H2)⊥上的对偶Toeplitz算子.下面,我们给出Dφ的数值域和二次数值域的刻画:

定理6设φ∈L∞,u为阶大于1的内函数,则

证根据Dφ的表示(7)式以及引理2,可得

W(tφ)⊂W2(Dφ)⊂W(Dφ)

从而

可得

W(Dφ)⊂W2(Mφ)⊂W(Mφ)

从而

因为

故

φ(D)⊂W(tφ)⊂W2(Dφ)⊂W(Dφ)⊂W2(Mφ)⊂W(Mφ)

从而

因此可得

结论得证．