贸易去中心化对港口供应链的冲击效应

王 圣

(山东社会科学院 海洋经济文化研究院，山东 青岛266071)

一、引 言

近年来，国际贸易出现了明显的去中心化趋势，贸易份额的集中程度不断降低。相应地，区域间的贸易大幅度增长，贸易中心逐渐向不同区域扩散，东南亚国家联盟(ASEAN)、东盟、澳大利亚和新西兰自由贸易区(AANZFTA)、欧洲自由贸易联盟(EFTA)、欧洲联盟(EU)、区域综合经济伙伴关系(RCEP)、金砖国家(BRICS)等协议成员内部的贸易频率要远远高于对外的贸易活动[1]。从2019年开始，新冠疫情的爆发导致基于原有分工秩序的贸易体系逐渐瓦解，各国纷纷采取贸易收缩策略，尽量安排国内生产，以保证供应链的安全稳定性，这进一步加剧了贸易去中心化的趋势[2]。

在此背景下，物流企业开始构建更为扁平化的运输结构以适应贸易中心的分散，主贸易航线上钟摆型的物流模式正逐渐被辐射型的物流模式所取代[3]。贸易结构的转变改变了行业的竞争秩序，并促使物流部门建立新的核心能力，在这一过程中，大部分物流核心功能的重建和改进都是在港口供应链的基础下进行的[4]。归纳上述现象可以发现，宏观贸易环境决定了物流部门在既定政策背景下核心竞争力的构建方式，而核心竞争力的转变决定了节点企业的行动策略以及整体的物流结构。因此，通过港口供应链贸易效应的分析，可以总结物流部门在新贸易形势下的行为逻辑以及由此衍生出的物流结构。

根据上述研究思路，港口供应链的适应性变化应以贸易环境的转变为起点，笔者将通过文献综述的形式总结当前贸易格局的主要特征以及港口供应链核心竞争力的构建形式，在此基础之上，利用新古典经济学模型为港口供应链企业的行为策略提供经济学解释，并根据面板向量自回归模型对各决策变量间的理论关系进行验证，最后对全文的主要结论进行整理。

二、文献综述

贸易去中心化并非是当代特有的现象，近代东北与上海之间的大豆、棉布贸易及柞蚕丝转口贸易也出现过类似的变动趋势。1840年前后，上海借助江海交汇以及地处中部的区位优势成为我国最大的航运中心，由于南北方自然条件差异显著，商品贸易的互补性较强，通过网络密布的运河航道，在进行国内贸易的同时，东北生产的农产品大部分经由上海出口到日本、美国等地。但在1850年之后，由上海运往东北的商品结构出现了明显的变化，从棉花、布匹、茶叶逐渐转为洋货[5]。同时，东北港埠的开放使得土货不再依靠上海中转出口，洋货也直接从日本进口，东北和上海之间传统的往来贸易显现出衰退的迹象，上海贸易中心的地位也由于贸易航道的改变以及新商埠的出现而不断下降。这一变化对当时的航运业产生了巨大的影响，由于国内南北贸易被外贸取代，往来于大小运河航道的沙船运输业逐渐衰落，并最终在外商垄断和航运技术差距的压力下彻底消失。

二战结束后，美国凭借美元的中心地位成为世界最大贸易进口国，而欧洲各国也在美国的帮助下逐渐从战争的阴影中走出，率先实现了经济的复苏，欧美之间贸易的繁荣使得贸易中心逐渐聚集。进入21世纪后，多次金融、经济危机的爆发和亚洲地区经济的强势复苏使得全球经济再次进入了平衡发展的状态，贸易空间结构开始出现分散化的趋势[6]。在这一背景下，航运物流业的格局也在随之发生变化，原先作为欧洲、美洲货物集散中心的高雄港和釜山港，在长江三角洲腹地经济高速发展的竞争压力下，其航运中心的地位在不断降低，大量亚洲出口欧美的货物开始通过上海港、宁波—舟山港进行转运[7]。这一转变增加了海运行业的货源收集难度，并迫使其与更多的港口建立灵活的业务联系，使港口供应链出现了网络化的结构。

受新冠疫情的影响，全球范围内各国生产环节出现同步性差异，基于国际分工的比较优势逐步削弱，而协同成本却进一步上升。这导致原先的多边主义框架受到巨大冲击，出于国家安全的考虑，各国纷纷将产业链移至国内，使全球产业链出现区域化、碎片化的现象，中国作为全球制造业中心，受到的冲击尤为剧烈[8]。实际上，在新冠疫情发生之前，西方国家就存在一种观点，认为供应链的过度集中和单极化趋势极易引发战略风险，特别是在一些关键领域，一旦发生突发事件，将导致全球产业链布局的崩溃[9]。出于国家安全的考虑，不应将大部分的产业链节点集中于某一国家，而应采取更具弹性和多元化的方式，将产业链分散于不同的国家和地区。新冠疫情的爆发加速了这一去中心化的进程，未来的产业链布局很可能呈现出分散化特点[10]。在这一供应链外移作用的推动下，全球供应链布局最终将向终端消费者集聚，并形成仅具有弱关联甚至相互隔离的区域性供应链。

可以看出，历次贸易格局的演变均对港口、航运等港口供应链节点行业造成了系统性的冲击。近年来，随着贸易低迷状态的扩散，传统贸易中心的地位和作用也在不断弱化[13]。与之相反，作为建立贸易新秩序的尝试，区域间的贸易往来则逐渐升温。这一贸易去中心化的趋势势必影响港口供应链的整体收益以及节点部门的行为模式。

三、基于贸易离散效应的港口供应链模型

(一)背景与前提假设

随着美国经济主导地位的逐渐减弱，以此为基础的国际贸易格局也在发生变化。在此背景下，各国均试图建立以自身为中心的贸易新秩序，其主要的表现就是传统全球贸易中心的地位不断降低，而在区域合作组织(协议)框架下的地区间贸易则发展迅速。这意味着与之相关联的任何贸易活动都将不可避免地受到影响，在国际货物运输领域，商品在不同贸易航线上的比例变动是造成这一影响的直接原因[11]。与此同时，贸易格局的变化以及未来趋势的不确定性导致运输部门采取合作的方式应对风险，通过彼此竞争优势的整合实现价值链的重构，其中最典型的方式就是港口供应链整合。这种以任务为导向的灵活的组织结构，通过链接运输活动中的各个节点企业，以供应链收益最大化为目标，实现了竞争优势的重构，使所有节点企业的竞争力最终以供应链的方式体现出来。因此，在供应链的框架下讨论贸易去中心化对运输部门的影响更加符合当前的环境，而分析的重点则主要集中在不同贸易航线上的货运比例的变动对供应链的运力、资本以及节点企业物流服务均衡价格的影响。

港口供应链对贸易去中心化冲击的反应依赖于节点企业的联合决策，为建立准确的节点企业行为函数，需要对上述背景框架的一些具体细节进行设定。在港口供应链的结构方面，节点部门的类型包括：(1)陆上运输部门，如集卡运输公司、铁路货运公司等，主要负责港口至腹地企业的路上运输。(2)港口部门，按照港口的区位和货物吞吐量分为主线港和支线港两类，其中支线港又分为更靠近贸易主航线的沿海港口和更靠近腹地的内陆港口两类。(3)海运部门，如马士基等大型船公司，主要提供海上运输服务，船公司将根据具体的市场需求在贸易主航线和支线上合理配置运力[12]。在贸易去中心化的函数表达方面，为准确描述货物运输的分布变化，图1根据起讫港的特征对其进行分类(见图1)。全部贸易货物按运输线路分为主航线运输货物和支线运输货物，比重分别为1-α和α。其中，主航线运输货物分为直接由主航线启运以及由支线港启运再经主线港转运2种类型，比重分别为1-β和β。经主线港转运的主航线货物中，由沿海支线港启运的货物比重为μ，由内陆支线港启运的比重为1-μ。由于支线港口之间不一定存在直达航线，此时需要通过主线港进行转运，因此，所有的支线运输货物分为经主线港转运的支线货物以及由支线港直接运输的支线货物两类，比重分别为1-γ和γ。与主航线运输货物的情形相同，ν和ω分别代表相应类型下由沿海支线港口启运的货物比例，1-ν和1-ω为内陆港口启运的货物比例。

图1 港口运输货物分类

在考虑上述背景的前提下，还需要对港口和班轮公司的特征及行为进行刻画，具体假设如下：

假设1：基于货物运输平衡的要求，供应链各节点处理的进口和出口货物数量相等[14]。尽管存在贸易不平衡现象，但如果从全球贸易的角度考虑，进口和出口数量必然是相等的。

假设2：物流节点的拥挤成本随适应度(处理能力与实际处理量之比)的倒数呈指数式增长[15]。贸易格局的改变要求企业对物流资源(运输车队规模、港口码头设施、船舶运力及规模等)的配置进行及时的调整，如果资源配置不合理出现货物积压，则要支付额外的拥挤成本。

假设3：港口部门由1个主线港和2个支线港构成，其中支线港的区位特征存在差异。沿海支线港更靠近贸易主航线，货物海上运输距离较短，在干线运输上具有优势；内陆支线港距腹地较近，货物陆上运输距离较短，在货源收集上更具优势[16]。

假设4：港口供应链节点部门的边际收益不变，即每增加一单位(装卸或运输)货物所获得的利润是相同的。

假设5：模型仅考虑短期内贸易格局变化对港口供应链的影响，因此，港口供应链节点部门的规模和物流处理能力不变。

上述背景和假设为港口供应链节点企业的行为提供了一个基本的框架，在此框架下，企业将根据利润最大化原则进行独立决策。为考察贸易去中心化的影响，首先推导出节点企业决策变量的最优反应函数，并将其代回企业的行为函数，最后求出货物分布的变化对最大收益值的影响。

(二)港口供应链节点部门的利润函数

根据前文的分析，港口供应链的节点企业包括陆运公司、沿海支线港、内陆支线港、主线港、班轮公司，其行为函数均以利润最大化为原则建立。

πh={dm(1-α)(1-β)+df1[(1-α)βμ+

α(1-γ)ν+αγω]+df2[(1-α)β(1-μ)+

α(1-γ)(1-ν)+αγ(1-ω)]}

(1)

其中πh为陆运部门的利润，dm为腹地至主线港m的陆上运输距离，df1为腹地至沿海支线港f1的陆上运输距离，df2为腹地至内陆支线港f2的陆上运输距离，Q为总货运量，bh为陆运部门的滞期成本系数，kh为陆运部门的货物运输能力，ph、ch分别为陆运企业单位运输价格和成本。根据假设3可知，df1>df2。

2. 港口部门。港口部门由1个主线港和2个支线港构成，滞期成本与陆运部门类似，因此，主线港m的利润函数为：

πm=[1-α+α(1-γ)]Q(pm-cm)-

(2)

其中，πm为主线港m的利润，pm为主线港的单位货物装卸价格，cm为主线港单位货物装卸成本，bm为主线港m的拥堵成本系数，km为港口m的设计吞吐能力。

沿海支线港f1的利润函数为：

πf1=[(1-α)βμ+α(1-γ)ν+αγω]

Q(pf1-cf1)-

(3)

其中πf1为沿海支线港f1的利润，pf1为港口f1的单位货物装卸价格，cf1为港口f1的单位货物装卸成本，bf1为支线港f1的拥堵成本系数，kf1为港口f1的设计吞吐能力。

内陆支线港f2的利润函数为：

πf2=[(1-α)β(1-μ)+α(1-γ)(1-ν)+

αγ(1-ω)]Q(pf2-cf2)-

其中πf2为内陆支线港f2的利润，pf2为港口f2的单位货物装卸价格，cf2为港口f2的单位货物装卸成本，bf2为支线港f2的拥堵成本系数，kf2为港口f2的设计吞吐能力。

3.海运部门。海运部门的物流功能是提供海上运输服务，根据不同货物的运输要求和利润最大化原则，海运部门需要在不同的贸易航线上合理部署运力。为直观地表述运力分配的情况，对分配的比例进行了说明(见图2)。其中主航线运力为连接主线港的航线上的运力，支线运力为连接支线港的航线上的运力，喂给航线运力为连接主线港与支线港的航线上的运力。ρ、θ、λ分别为相应的运力分配比重。

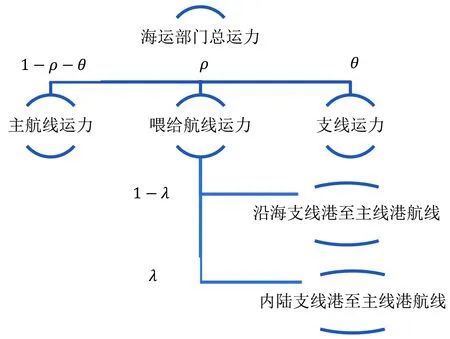
图2 海运部门的运力分配

此外，与港口部门相同，海运部门也会由于运力分配不合理而产生相应的滞期成本，因此，海运部门的利润可表示为：

πl=(1-α)Qlmm(pmm-cmm)+[(1-α)βμ+

α(1-γ)ν]Qlmf1(pmf-cmf)+[(1-

α)β(1-μ)+α(1-γ)(1-ν)]Qlmf2(pmf-

(5)

其中，lmm为主航线海运距离，lmf1为支线港f1至主线港的海运距离，lmf2为支线港f2至主线港的海运距离，lff为支线港之间的海运距离，pmm、pmf、pff分别为主航线、喂给航线、支线的海运价格，cmm、cmf、cff分别为主航线、喂给航线、支线的海运成本，bmm、bmf、bff分别为主航线、喂给航线、支线的滞期成本系数，kl为海运部门总运力。

(三)带参数的多元最优化求解

通过上述模型的构建，贸易去中心化的港口供应链优化问题转化为货物分布状态变化条件下的港口节点企业收益最优化问题。根据包络定理，处理价值函数的最优化问题时，需要先获得内生变量对因变量的最优反应函数，即各节点企业的决策变量对总收益的最优反应函数，因此，应首先确定各节点企业的决策变量与其他自变量之间的关系。

在各节点部门的利润函数中，决策变量为物流服务的价格p(ph，pf1，pf2，pm，pmm，pmf，pff)，根据假设5，需求Q是唯一受价格影响的内生变量，因此，应首先建立节点部门的价格需求函数。最常用的需求函数形式主要为一般线性和对数线性2种，其中一般线性需求函数缺少合理的经济解释，同时不满足0阶齐次性条件，因此采用对数线性需求函数较为合理，即：

lnQ(p)=A+∑gilnpi

gi=[gh，gf1，gf2，gm，gmm，gmf，gff]，

pi=[ph，pf1，pf2，pm，pmm，pmf，pff]，A∈R

(6)

其中，gi为价格i的弹性系数。将(6)式代入(1)-(5)式，分别对决策价格求偏导并令其为0，即可得到相应的最优反应函数：

α(1-γ)ν+αγω]+df2[(1-α)β(1-μ)+α(1-γ)(1-ν)+αγ(1-ω)]

(7)

(8)

(9)

(10)

(11)

α(1-γ)ν，τmf2=(1-α)β(1-μ)+α(1-γ)(1-ν)

(12)

(13)

由于使用了对数线性需求函数,导致无法求出各决策变量的解析解,因此(7)-(13)式中仍保留了变量Q。将(7)-(13)式代入(1)-(5)式中,并将其加总可得:

(14)

式中πt为供应链整体的总收益，可以看出，πt由5个部分构成，分别是陆运、主线港、沿海支线港、内陆支线港、海运5个港口供应链节点的收益，ph(·)、pm(·)、pf1(·)、pf2(·)、pmm(·)、pmf(·)、pff(·)分别为(7)-(13)式所代表的最优反应函数。

(四)均衡结果分析

贸易去中心化对港口供应链的影响可以由πt对α、β、γ、μ、ν、ω的偏导表示，其主要推论如下。

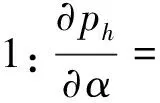
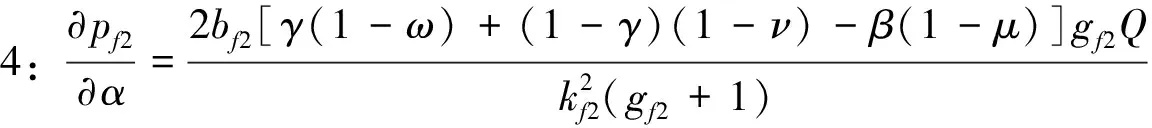
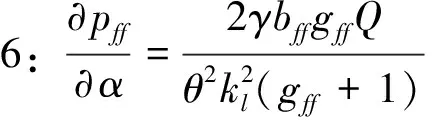
推论7：pmf=

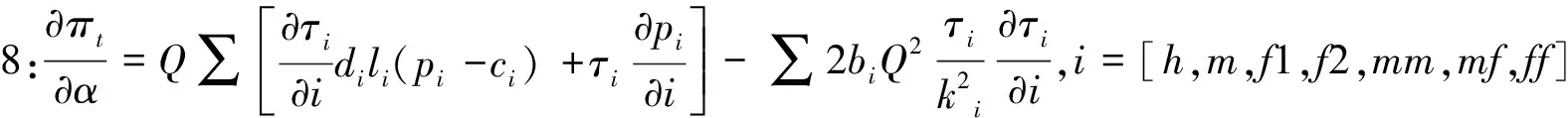
由推论1可知，贸易去中心化对陆运部门价格的影响取决于从主线港启运的货物周转量与从支线港启运的货物周转量之间的大小，当前者大于后者时贸易去中心化将提高陆运部门的服务价格，反之则降低服务价格。此外，影响的程度还受到陆运拥挤系数和陆运部门收益比重的正向影响。

推论2-4的结果显示，在港口部门内，贸易去中心化将导致主线港口装卸价格的下降，下降的幅度与主线港拥挤系数和主线港在供应链中收益比重正相关。对支线港价格的影响取决于其装卸的支线运输货物和主线运输货物的比重，当支线货物比重较大时，贸易去中心化趋势将提高支线港的装卸价格。与主线港的结果相似，提价的幅度与支线港拥挤系数及支线港在供应链中收益比重正相关。

根据推论5、6可知，对海运部门来说，贸易去中心化趋势将降低主航线货物的运输价格，但船公司在主航线上运力部署的增加将弱化这一影响。与之相反，支线货物运输价格受到的影响总体为正，支线运力的大小与影响程度呈负相关关系。此外，滞期成本系数和支线运输收入在总供应链中的比重放大了贸易去中心化的影响效果。

推论7的结果说明，贸易去中心化对喂给航线运价的影响取决于主航线和支航线之间货物周转量与拥挤成本的关系。分子中[β(1-μ)+(1-γ)(1-ν)]lmf2表示经由喂给航线的主线货物与支线货物之间的周转量差额，(1-λ)2τmf1(ν-βμ)+λ2τmf2[β(1-μ)+(1-γ)(1-ν)]表示经由喂给航线的主线货物与支线货物之间的拥挤成本差额。因此，当经由喂给航线的主线货物与支线货物在周转量和拥挤成本上的差额符号相同时，贸易去中心化将降低喂给航线的运价，若符号不同则提高运价，但船公司可以通过调整运力分配影响拥挤成本，进而控制贸易去中心化对喂给航线运价的影响。

从推论8的结果中可以看出，贸易去中心化对港口供应链总收益的影响较为复杂，由于使用了对数线性形式的需求函数，导致无法写出准确的解析解。但从推导结果的形式来看，贸易去中心化对供应链总收益的影响可以分为2个部分：(1)对各物流节点部门价格的影响，这一点在推论1-6中已经做出详细说明。(2)通过价格对各节点货物处理量产生的间接影响，其中节点部门的拥挤(滞期)成本系数及收益比重与影响效果呈正相关关系。

四、主要研究结论

通过建立包含陆运、港口、海运3个部门的博弈模型，贸易去中心化趋势对港口供应链的影响可以归纳为以下几点：(1)港口部门和海运部门的传统主线节点将受到确定性的负面影响，因此，价格下降和运量减少的共同作用将缩减主线港和主航线班轮公司的利润空间。(2)陆运部门运价的反应取决于主线运输与支线运输货物周转量的大小，对支线港口装卸价格的影响取决于其装卸的支线运输货物和主线运输货物的比重，如果仅考虑总体运价反应，则贸易去中心化趋势必将导致支线港装卸价格的上升，但由于支线货运量的增加将在内陆支线港和沿海支线港之间分流，因此不同类型支线港受到的冲击也有所差异。(3)支线货物海运价格受贸易去中心化的影响总体为正，但港航业收益的分流程度小于货源分流的程度，大型港口在货源集聚上的优势弱化了这一去中心化的趋势。