双射流等离子体反应器大涡模拟研究

袁 祥,陈仙辉,周 旭,夏维东,叶桃红

(中国科学技术大学 工程科学学院,安徽 合肥 230027)

电弧等离子体具有高温、高焓和高化学活性的特点,在涂层和表面处理[1-2]、冶金[3-4]、微纳米材料制备[5-7]等领域有着广泛的应用。例如等离子体法热解煤制乙炔CO2排放低、耗水量较少,可以得到比传统方法更高的乙炔收率[8-9];等离子体直接热解燃料制备炭黑,可以避免氮氧化物生成的同时副产物是氢气,原料的利用率与转化率很高[10];等离子体喷涂技术[11]在对颗粒加热的过程中,数千度的高温可使化工原料熔融,并通过高速射流将其冲击到基板表面形成涂层。虽然电弧等离子体技术在各类工业生产中已经得到了充分的发展,但还是存在一些技术瓶颈。煤粉裂解乙炔过程中等离子体射流与固态煤粉接触面小,难以均匀加热煤粉,乙炔的收率得不到进一步的提高。由于电弧能量过于集中,制备炭黑时反应场温度不均匀,产品一致性较差。而等离子体喷涂技术中射流的核心区域温度远远高于其他区域,颗粒难以完全进入高速的射流核心区,部分颗粒的加热不完全,基板涂层的均匀性难以达到工业标准。因此,为了弥补电弧等离子体能量集中、等离子体-冷物料混合困难,产生温度均匀的大面积电弧等离子体加强混合尤为关键。

早期的等离子体发生器往往是单炬的结构,单炬产生的等离子体射流的功率随着工业的发展存在逐渐变大的趋势[12-13]。轴线式等离子体炬的出口处温度的分布极不均匀,温度的脉动幅度会达到百分之几十,而磁驱动电弧正是对这一问题进行改进,磁场的作用使电弧高速旋转,能够产生温度均匀的大面积热等离子体[14-16]。20世纪中后期英国、德国、美国[17]等都曾使用同轴式磁旋转电弧等离子体发生器进行裂解煤制乙炔的实验研究,美国的AVCO公司1MW功率的等离子体反应取得了中试实验成功。但是此类磁旋转电弧发生器的扩散电弧只有在大功率、强磁场的条件下才能保持稳定,且轴向方向的等离子体会呈现收缩状态,轴向长度较短,化工原料的加热过程比较短且运动轨迹杂乱,受热角度不均匀,有一定的局限性,要实现工业化会有很多瓶颈问题难以解决。为了产生温度均匀的热等离子体的同时满 足高功率、高效率的条件,双射流等离子体炬[18-20]以及多射流等离子体炬[21-23]逐渐发展起来。

本文基于双炬射流形式的等离子体反应器采用LES方法模拟研究炬轴向偏转角与动量比对内部流场结构、温度场以及流体混合的影响。在此基础上,通过调整反应器的结构参数得出了最大效果获得大面积高温、温度均匀等离子体的方法,可用于指导等离子体反应器结构优化和各类热等离子体化工原料生产。

1 数值方法和几何模型

1.1 物理模型

图1(a)为该双炬射流反应器的几何结构与计算域示意图。反应器的顶部为冷空气入口,其直径大小为D=40 mm。两只射流炬以中心轴线为基准对称布置在反应器上,射流入口直径为Da=20 mm,反应器整体长度L=500 mm,直径R=150 mm。图1(b)展示了该反应器的轴向截面,α为炬与竖直面之间的夹角,α的大小分别为30°、45°、60°与90°。

图1 反应器物理模型

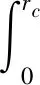
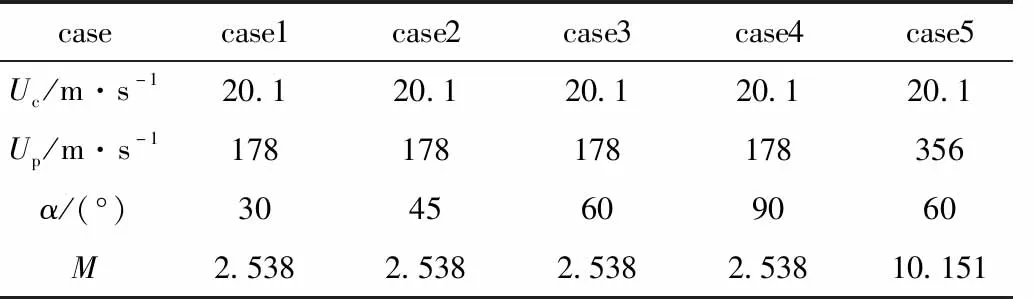
表1 双炬射流的流动参数

1.2 控制方程

本文运用LES方法研究了热等离子体双炬射流与冷空气射流的流动与混合特性的影响。

为了简化计算,不考虑反应器内部的化学反应,以空气作为等离子体气体,同时用冷空气代表碳氢化合物原料。针对本文的研究工作,采用了以下假设：

(1)等离子体处于局部热力学平衡(LTE)态;

(2)忽略辐射能量交换;

(3)重力忽略不计。

基于以上假设,在有限体积法求解的CFD平台OpenFOAM,使用植入了Navier-Stokes与能量方程的rhopimpleFoam求解器,笛卡尔坐标系下可压缩的控制方程为

(1)

(2)

(3)

τij为分子黏性力,其表达式为

(4)

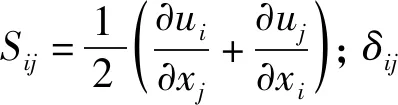
1.3 数值方法

rhopimpleFoam求解器使用了SIMPLE与PISO结合的PIMPLE算法,通过求解压力方程来确保质量守恒,再对现行的速度进行修正来满足动量方程。对流项的计算采用了二阶van-Leer-TVD格式,时间项为CrankNicolson格式,计算过程中为了保证数值的稳定性,动态调整计算时间步长,时间步长数量级为10-7s,同时保证库朗数小于0.5。

本文热等离子体射流入口处的速度与温度满足以下分布：

T(r)=(Tm-Tw)[1-(r/R)4]+Tw

(5)

v(r)=vm(1-(r/R)4)

(6)

其中Tm=3 000 K为热等离子体温度,Tw=300 K为反应器壁面温度。热等离子体与冷空气的vm分别为178、20.1 m/s,同时为两股射流的平均速度添加白噪声以实现2%的湍流入口速度边界条件;出口处为总压边界条件,压力为1atm;壁面为处温度与压力分别为300 K与1atm,速度为无滑移边界。

1.4 网格独立性校验

反应器计算域的网格使用结构化网格划分的策略,选取三套网格,网格总数分别为250万、500万与800万,利用这三套网格对比了反应器内轴线处平均温度的变化规律。根据反应器长度L对轴向距离z进行无量纲化,令z/L=0为冷空气入口处,从图2可以看出,500万网格与800万网格的算例情况下,轴线处温度峰值相同,后续的温度分布差异几乎可以忽略不计。综合考虑仿真精度以及计算所需时间等因素,本文采用500万网格数量的模型进行双炬射流等离子体反应器数值模拟。

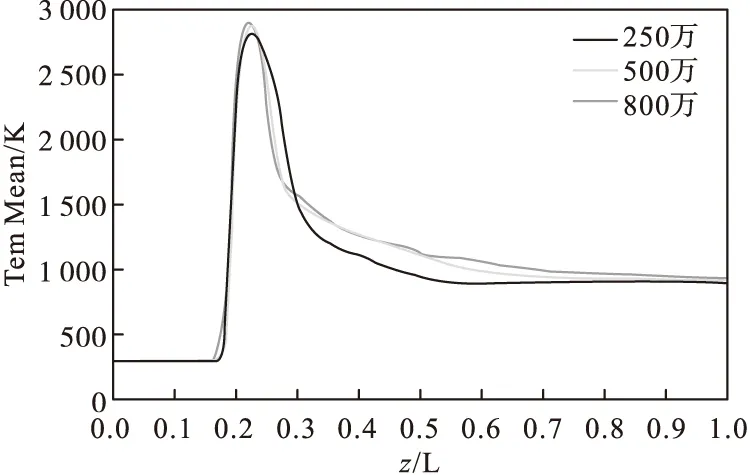
图2 网格独立性验证

2 结果与讨论

对表1中的六种工况进行LES模拟分析,研究了双炬射流反应器内不同炬轴向偏转角与热等离子体射流动量比对空气等离子体射流平均流场、瞬时流场、湍流统计特性、涡量特征及混合特征的影响,并得出了最大效果获得大面积高温与温度均匀热等离子体的方法。

2.1 平均流场

根据冷空气入口直径与反应器长度对径向长度与轴向长度进行无量纲化,case1～case6的平均温度的分布如图3所示。等离子体反应器双炬在x=0截面对称布置,高温等离子体射流会沿射流方向中心区域对撞,部分热等离子体气体会向上反冲与入口处的冷空气射流对撞,形成回流区。随着偏转角的增大,射流高温区域会向反应器上游偏移,回流区域增大,同时冷空气与热等离子体的混合区域也随之增大。在不改变偏转角的情况下改变热等离子体射流动量比,反应器内回流区与混合区域的面积保持不变,内部温度更加均匀,对于动量通量比最大的case6,反应器内平均温度趋于2 000 K。

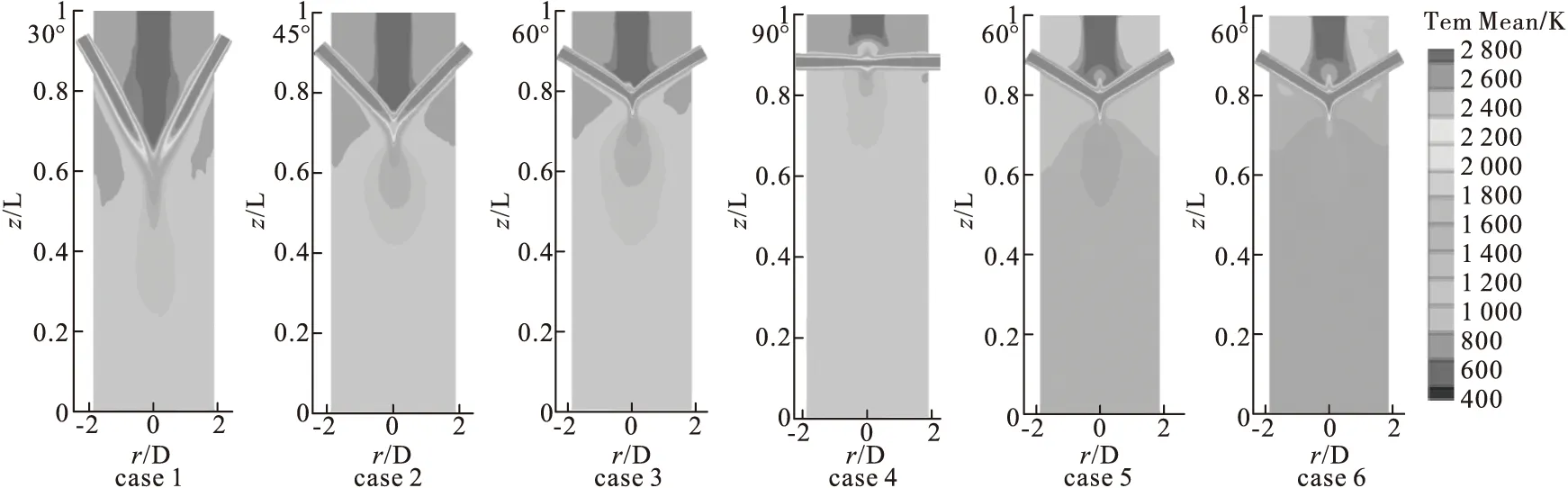
图3 case1～case6中x-z截面的平均温度分布

图4展示了case1～case6中x-z截面上的平均轴向速度与流线分布、图5展示了case1～case4中对撞中心处x-y截面的流线分布。其中,对于偏转角从30°到90°的情况下,对撞中心处指的是z=(70+zh)mm处,zh为炬与壁面的下交点到两炬交点中心的竖直距离。混合过程中以对流为主要机制的区域定义为混合区[26],从图4可以看出,在小角度的情况下冷气流会以较高的速度直接穿过混合区域,在混合区域的停留时间较短,冷气流与热等离子体射流因对流而产生的换热相对较少。另外,两股射流对撞后一部分沿中心轴线流动,另一部分沿壁面流动,沿壁面流动的射流撞击壁面后会与轴线处的射流形成沿轴线对称的两个涡旋区,随着偏转角逐渐增大,涡旋区的位置越来越靠近上游。在不改变偏转角的情况下改变动量比,如图4中的case3、case5、case6,轴向速度随着动量比成倍增加,但流动区域的流型不会发生改变。

图4 case1～case6中x-z截面的平均轴向速度与部分流线分布

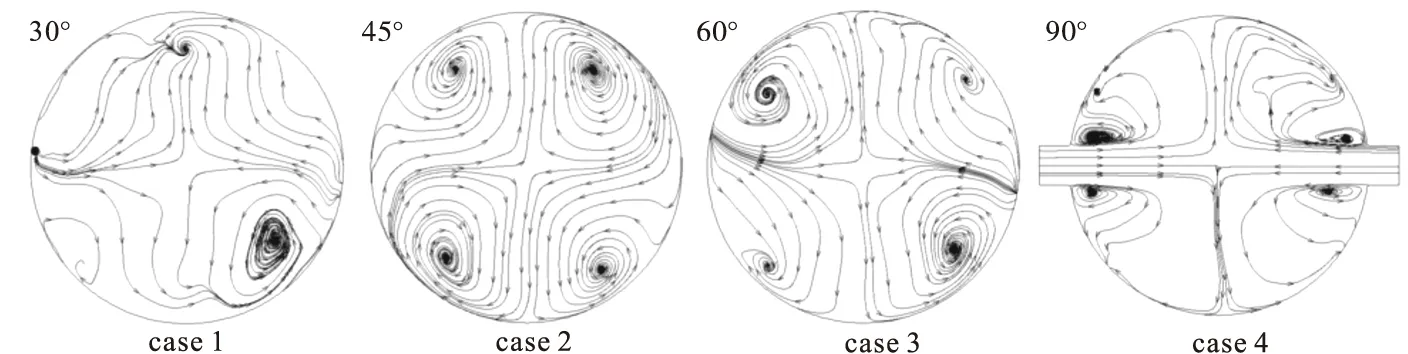
图5 case1～case4中对撞中心处x-y截面流线分布

观察图5中的流线分布可以得出,不同角度下的射流发生碰撞后形成涡旋的形态和数量有所不同,case1中,两股高温射流的主体部分沿正向流动形成涡旋,其余部分因为旋流作用较弱,被卷入对撞流动的涡旋之中,因此图中只有一个涡旋对的存在,这种模式下流型为吞没流型。在θ>45°之后,对撞后的高温射流形成了大小不一的两个涡旋对,case1模式下的一对涡旋依然存在,不同的是两股射流的小部分流动又分为两部分,一部分被对撞流卷吸,一部分沿反方向流动形成较小的涡旋,因此图中展示的是一大一小的两个涡旋对,而随着偏转角继续增大至90°,两股高温射流对撞后,一分为二沿着反向流动,最终形成了四个对称的涡旋,这种模式的流型称之为涡流型,这也说明了炬偏转角增大的过程也即流型由吞没型向涡流型的转变过程。

令z/L=0代表冷空气入口处,图6为case1～case6炬中心轴线上平均温度、平均轴向速度与平均空气质量分数的变化。从图6中可以得出,当偏转角发生改变后,平均温度、平均轴向速度与平均热等离子体质量分数的峰值的大小和位置都会发生改变。图6(a)中虚线为平均温度为2 000 K的等值线,在不改变动量比的情况下,不同偏转角算例下最终达到均匀分布情况的温度都是相当的,偏转角为30°时,轴线处的最高温度达不到2 000 K,而偏转角为60°与90°的峰值温度相近,不同的是90°偏转角的算例下,平均温度达到稳定后的情况所需要的流动距离更短。不改变偏转角而改变动量比后,平均温度的变化规律相似,不同的是更大动量比所达到的稳定温度更高。图6(b)中的虚线为平均轴向速度为0 m/s的等值线,当Uz>0也就意味着射流向上游流动,当偏转角大于45°之后,反应器内部开始出现因为逆流而形成的回流区,这种情况下相当于增加了冷空气与热等离子体的再循环区,更有利于它们之间的快速混合。分析图6(b)和图5(c)可以发现,偏转角为60°与90°的算例轴向速度分布近乎成对称状,且这两种情况下的平均空气质量分数相近。

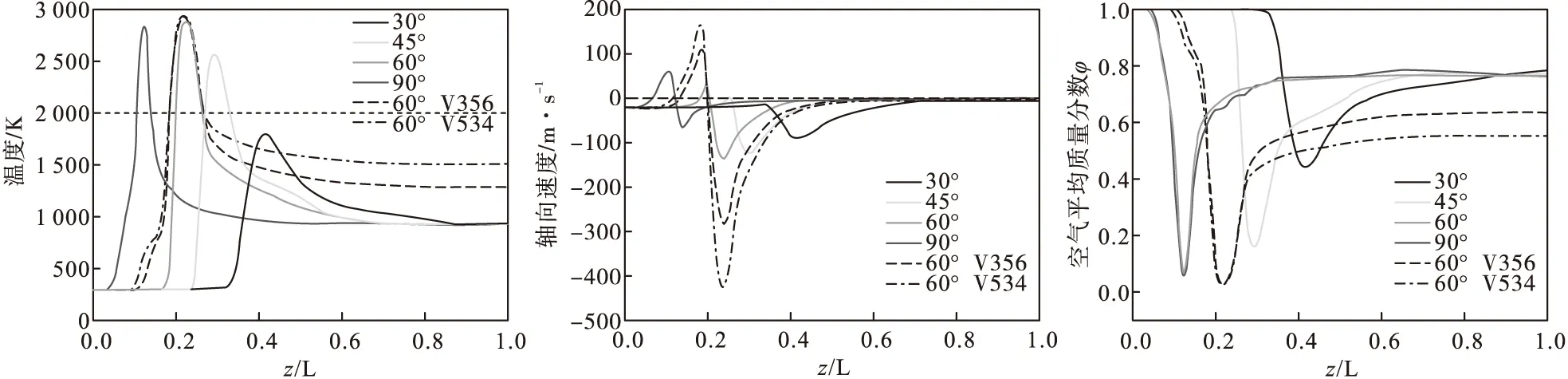
图6 case1～case6轴线处的平均温度、平均轴向速度、空气平均质量分数

2.2 瞬时流场

将高温射流通过计算域的时间0.04 s作为一个周期,计算20个周期后流动已经达到稳定,图7～图10展示了case3与case4在x-z截面上流动稳定后瞬时温度、瞬时轴向速度随时间的演化。从图7～图8中可以发现射流轴线不会完全对称,尤其是在混合层附近,对撞面不会保持稳定,而是发生了偏移,两股高温射流对撞后会偏向同一方向流动,这种现象在撞击流中被称为偏斜振荡[27-28],这种不稳定的流动现象是喷流之间区域压力降低引起的,所有振荡相互作用的情况都会伴随着涡旋运动的形成。对比case3、case4中高温流体在混合区的停留情况,当偏转角达到90°时,两股高温射流沿反方向流动,冷空气进入回流区后会与热等离子体射流形成的涡旋快速混合,获得较为均匀的温度分布。

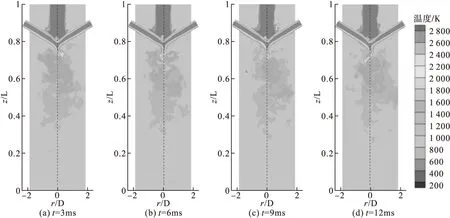
图7 case3中x-z截面瞬时温度分布随时间的演化

图8 case3中x-z截面瞬时轴向速度分布随时间的演化

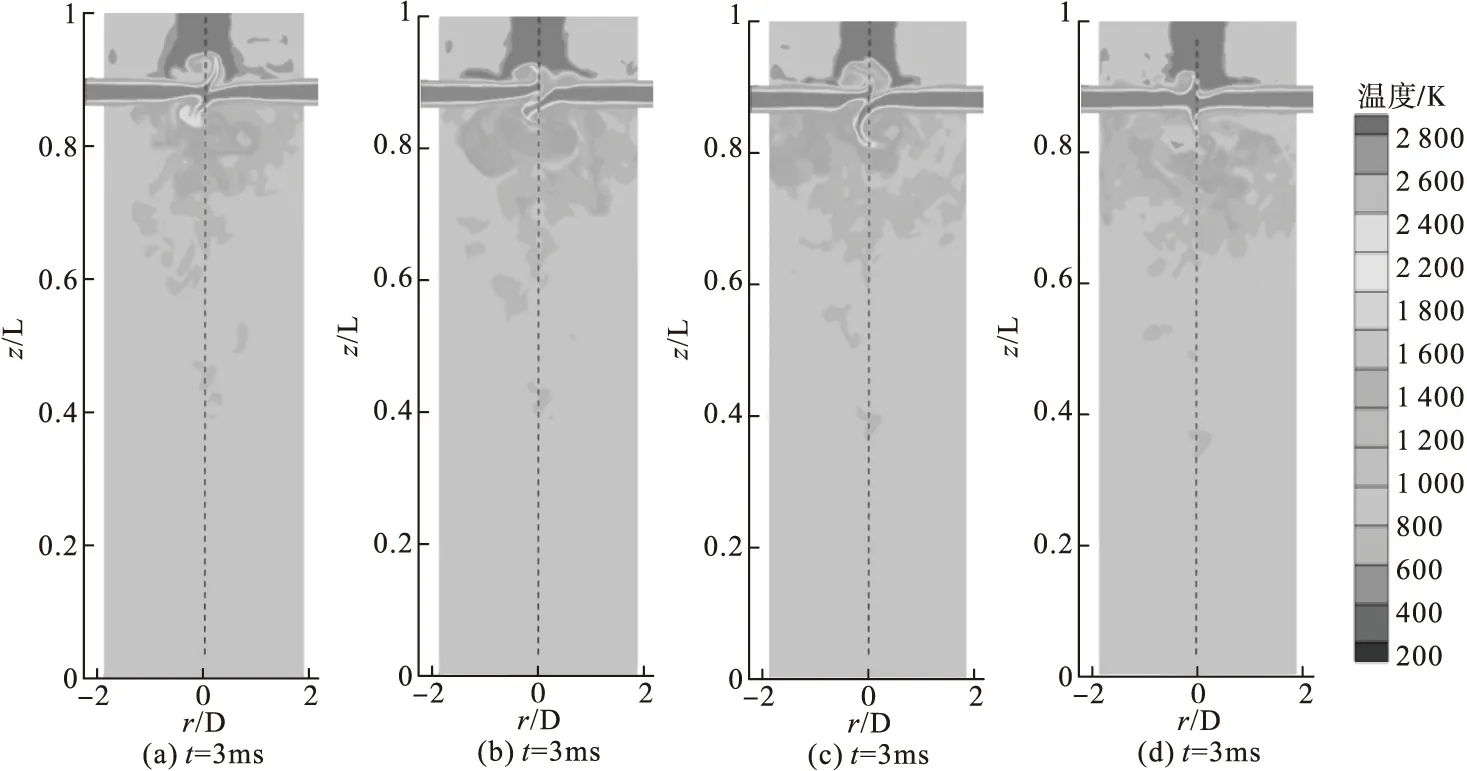
图9 case4中x-z截面瞬时温度分布随时间的演化

图10 case4中x-z截面瞬时轴向速度分布随时间的演化

为了表征冷空气与热等离子体射流混合过程中射流偏转角对瞬时流场结构的影响,引入了基于速度张量∇U的第二不变量Q准则[29]。图11展示了case1～case4中使用热等离子体气体质量分数着色的Q=30 000的等值面瞬时图。可以发现不同射流偏转角下,冷空气与热等离子体形成的涡结构明显不同。偏转角变大的过程中,两股射流的对冲作用增强,混合流体对壁面的冲击促成了周向涡的形成,周向涡对周围射流的卷吸作用较强,因此附近的冷空气质量分数相对更低,靠近冷空气入口的区域混合流体的涡环加强了流体的混合。射流偏转角较小时涡的破碎较为缓慢,当冷空气与热等离子体气体达到预期的混合后,涡结构的破碎现象更加显著,涡结构从形成到破碎的过程也即是冷空气与热等离子体射流的混合过程。

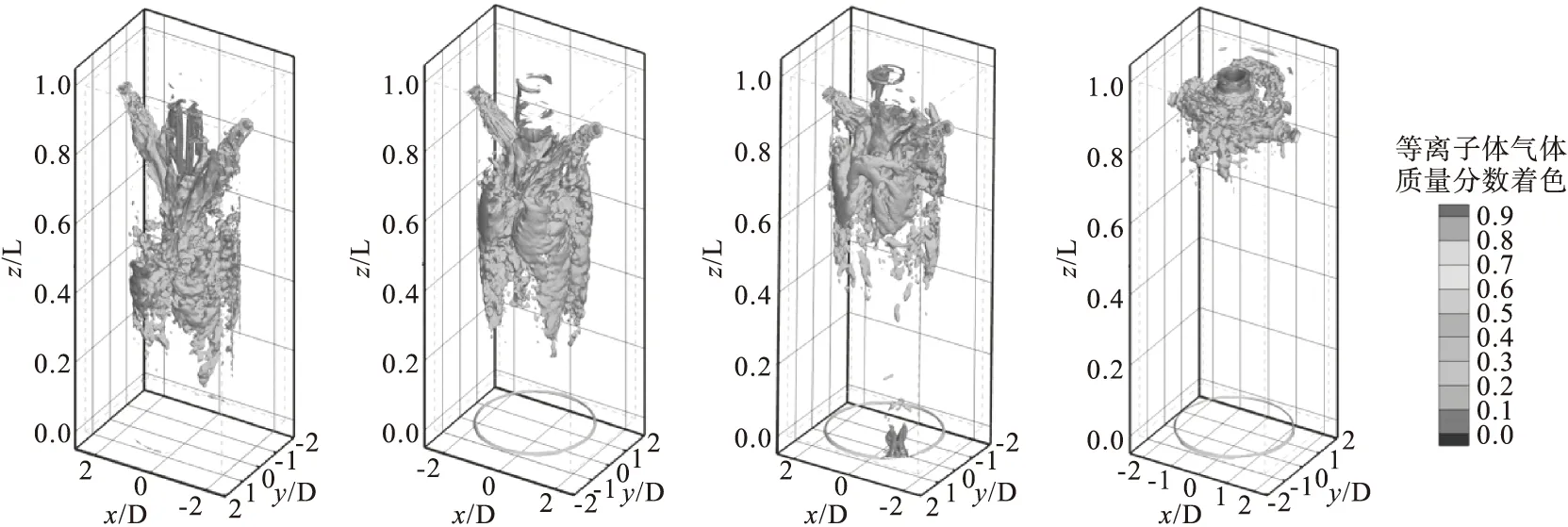
图11 case1～case4中Q准则等值面瞬时图,用热等离子体质量分数着色

2.3 湍流统计分析

图12 case1～case6中x-z截面的温度脉动

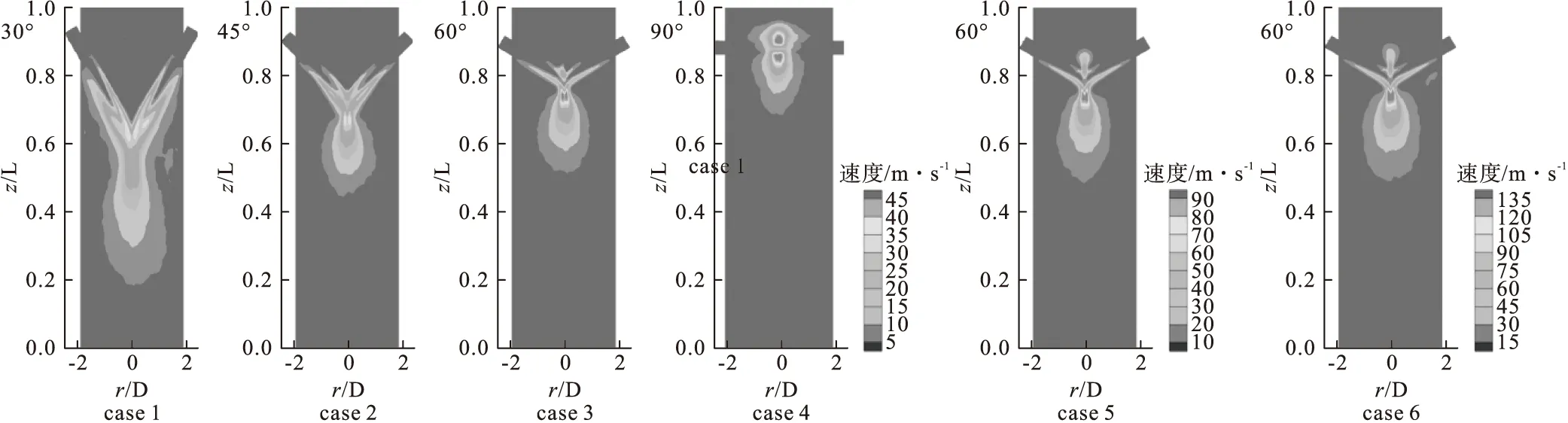
图13 case1～case6中x-z截面的轴向速度脉动

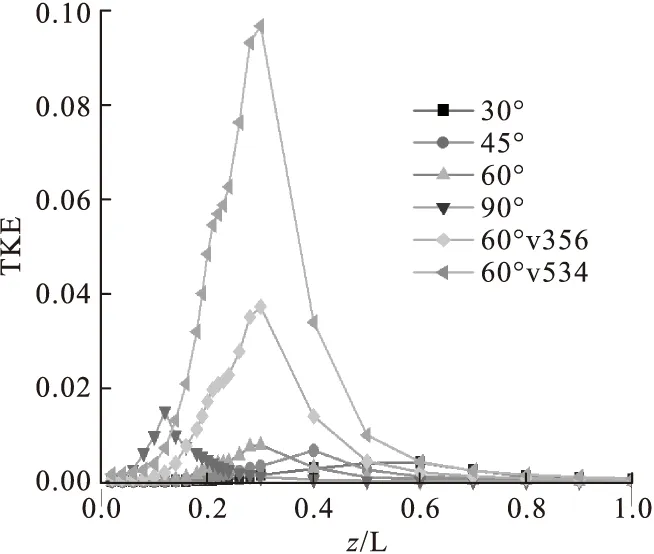
图14 case1～case6中不同x-y截面的湍流动能

2.4 混合特征

在双炬射流反应器中,混合区域的涡量越强,冷空气与热等离子体射流的卷吸混合效果越好。统计case1～case4中不同x-y截面的涡量大小如图15所示,各算例中涡量都为单峰值分布,分析发现图11中Q=30 000情况下的涡结构与涡量大小发展趋势相同。算例case4偏转角最大,涡量峰值位于回流区,形成的周向涡卷吸作用最强,当冷空气与热等离子体射流达到预期的混合后,即流向距离最短的混合区后,涡量大小急剧下降,此时的涡对混合流体的流动影响并不明显。而其他算例中涡量峰值大小相差不大,保持着经过混合区域后不断衰减的趋势。

图15 case1～case4中不同x-y截面的涡量

对于本文中冷气流与热等离子体混合的情况,采用描述方法[30]计算混合不均匀性β。

(7)

C为实际情况混合时等离子体气体的质量分数,C∞为理想混合时等离子体气体的质量分数,本文的双射流计算中C∞值对应射流速度178、356和534 m/s的值分别为0.36、0.47与0.57。β值的大小表征了理想混合情况与实际混合情况下等离子体气体质量分数的差异。观察图16可以发现各算例的β值在反应器中游之后保持稳定,对于不同偏转角度,增大偏转角后反应器内各区域段的β值降低。90°算例整体β值较小,且在混合初期,热等离子体射流反冲形成的回流区使得β值显著下降。而只是改变动量比的情况下,case4、case5、case6的β值在经过混合区之后变化不大。

图16 case1～case6中不同x-y截面的混合不均匀性

为了估算混合时间,更好地来衡量混合效果,将混合距离lm定义为混合不均匀性β最大值与最小值之间的轴向距离,混合时间τm将由τm=lm/v得出[31],v表示混合距离内的平均轴向速度。从表2的混合时间可以得出,在本文所研究的各个角度中,混合最快的角度为90°,并且混合时间远小于其他角度的算例,从前面的分析可以得出,该角度情况下对撞流产生的涡旋增加了各组分的接触面积,减小了混合距离,在小距离的温度脉动与速度脉动更显著,扩散效果更强,物料的混合效果更好。同时,在改变动量比也即增加热等离子体流量的情况下,冷气流与热等离子体的混合效果有显著的增强,这样的结果有利于开展后续四炬与六炬射流混合的模拟研究。

表2 case1～case6的混合时间 s

3 结 论

本文基于双炬射流形式的等离子体反应器采用LES方法模拟研究炬轴向偏转角与动量比对内部流场结构、温度场以及流体混合的影响。结果表明,冷空气与热等离子体射流的混合和炬轴向偏转角和热等离子体射流的流量有很大的关系,当炬轴向偏转角增大或增大动量通量比后两者的混合效果变得更好。

涡流的发展对混合特性至关重要,两股高温射流发生对撞后会产生偏斜振荡现象,振荡的相互作用会伴随着涡旋运动的形成。当偏转角增大后,涡旋对的数量会增加,混合流体流动模式会由吞没型转变为涡流型,混合层处涡量强度会提升,热等离子体射流对冷空气的卷吸作用加强了它们之间的混合。