探索知识本质,促发自然生成*——以向量的加法教学设计探析

福建省福清第一中学(350300) 林琳琳

福建省福清进修学校(350300) 林新建

人教版新课标教材《主编寄语》指出:“数学概念、数学方法与数学思想的起源与发展都是自然的,如果有人感到某个概念不自然,是强加于人的,那么只要一想它的背景,它的形成过程,它的应用,及它与其他概念的联系,你就会发现实际上是水到渠成、浑然天成的产物,不仅合情合理,甚至很有人情味,学习数学要摸索学习的方法.”本文以向量的加法教学设计为例,就如何引导学生探索知识本质,促发知识自然生成作一探析,以飨读者.

1 教学过程设计

1.1 数学情境,感知向量加法背景

教师:我们知道,力和位移可以合成,那么,向量是否可以合成?

追问:如果可以合成,合成的结果是什么?

设计意图:教师设置问题,让学生在熟悉的情境中感知向量加法的背景.学生会自然地由力和位移是向量,它们可以合成,从而想到向量当然可以合成,进而思考如何合成,合成的结果是什么,为新课的自然引入做好铺垫.

1.2 数学探究,抽象向量加法特征

教师:如图1,力F对橡皮条产生的效果与力F1与F2共同作用产生的效果相同,物理学中把力F叫做F1与F2的合力[3].合力F与力F1,F2有怎样的关系呢?

追问:你如何从向量角度加以表述?

教师:如图2,由于以前大陆和台湾没有直航,想从台湾去上海探亲,需乘飞机先从台北到香港,再从香港到上海,请问这两次位移的结果是什么?

追问:你又如何从向量角度加以表述?

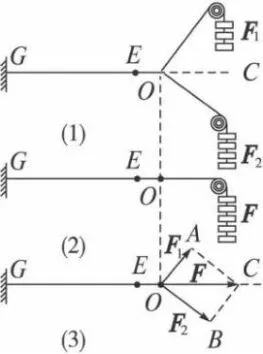
图1

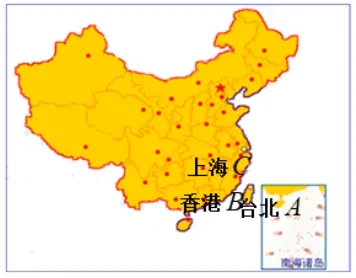
图2

设计意图:学生在教师的引导下,对上述现象进行了抽象,发现两个力F1与F2作用的结果与一个力F作用的结果相同,两次位移的结果与一次位移结果相同.

从向量的角度表述,即两个向量合成为一个新的向量.

1.3 数学体验,概括加法定义

教师:两个向量合在一起,形成一个新的向量,你认为两个向量是否进行了一次运算?根据“合成”可将这种运算命名为什么?

追问:你能对这个运算的定义加以概括吗?

设计意图:从运算角度看,力F可以看作是两个力F1与F2的“和”,向量也可以看作是向量与的“和”,从而很自然地得到向量加法的概念:求两个向量的和的运算叫做向量的加法,使向量加法定义的引入顺理成章,水到渠成.

教师:位移合成中的三个向量构成一个什么图形?能根据这个图形给这种加法运算法则一个名称吗?

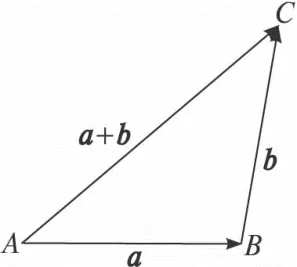
图3

师生活动:如图,位移合成中的三个向量构成三角形,所以给这个加法法则取个名字“三角形”法则.教师引导学生概括出三角形法则的特征.

追问:该如何用符号表示它呢?

教师:力的合成中的三个向量构成一个什么图形?如何给这种加法运算法则一个名称呢?如何用符号表示它呢?

设计意图:通过教师引导、学生动手操作,体验形到数、特殊到一般、具体到抽象,引领学生对向量加法法则特征的进一步感受,让学生获得足够的关于特征的体验,进而抽象出向量加法的三角形法则和平行四边形法则,其核心是动手体验到抽象概括,从而培养学生数学核心素养.

1.4 数学内化,掌握向量加法法则

教师:向量加法的这个两个法则是否一致吗?为什么[3]?

师生活动:教师引导学生动手操作体会:已知向量a,b,用两种运算法则求作向量a+b.

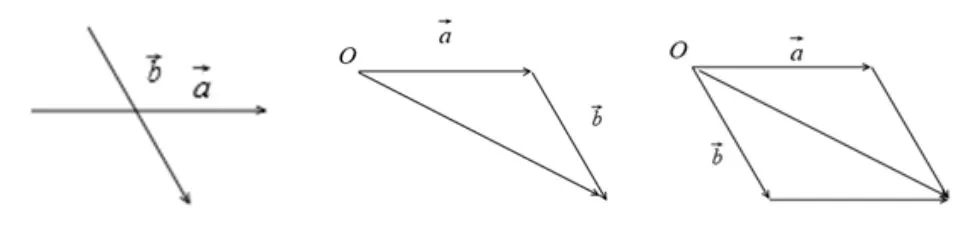
图4

通过学生动手操作归纳出向量加法三角形法则和平行四边形法则本质是一致.

设计意图:“主动学习的原则”是教学的一条重要原则,其核心思想是:学习任何东西的最佳途径就是靠自己去发现.教师要舍得留下足够的时间,让学生开展研究,以更好地培养数学抽象、逻辑推理等核心素养.

教师:如果向量a,b共线,类比数的加法,你又能得到什么关系呢?你能动手作出向量a+b吗?

追问:这时你能归纳出|a+b|,|a|,|b|之间关系吗[3]?

师生活动:教师提出问题,学生动手操作,可能个别学生不能得到正确答案,教师再进行讲解.再进一步让同学们回顾一般情况,进而巩固加深概念内涵.

设计意图:让学生经历一般到特殊的向量加法,再进行回顾,又经历特殊到一般,是为了更好让他们把握向量加法法则的本质,理解向量加法的内涵.这样比直接给一道向量加法法则运算题目,更能提高课堂效率.

1.5 数学应用,深化向量加法理解

教师:数的加法具有交换律、结合律,你能用图形语言证明向量加法的交换律和结合律?

师生活动:引导同学们通过自己动手设计图形来证明向量加法的交换律和结合律.教师可以进一步尝试让学生自己说出其设计的这种证明方法的思路.

设计意图:动手实践→准确表达,使得学生更进一步获得知识的内涵和本质,进而达到深度学习.这比教师事先画出图形,让学生理解概念运算律,要好的多.

教师:教材第9页例2长江两岸之间没有大桥的地方,常常通过轮船进行运输,如图所示,一艘船从长江南岸A点出发,以15km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东6km/h[3].

(1)试用向量表示江水速度、船速以及船实际航行的速度[3];

(2)求船实际航行的速度的大小与方向[3](用与江水速度的夹角来表示).

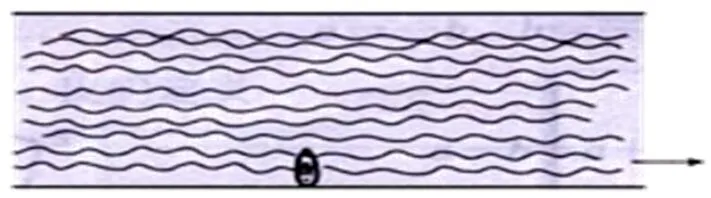
图5

设计意图:一方面,让学生经历生活→数学→生活,从而理解和表达现实世界中事物的本质、关系和规律.另一方面围绕概念的核心做辨析练习,以进一步巩固概念,促使学生把基本概念搞清楚,把握知识的本质,把握概念的内涵,促成能力和素养的提升.

2 教学设计体会

2.1 基于四能提出问题

为了使学生更进一步获得知识的内涵和本质,进而达到深度学习.教师在设置问题时,让学生动手操作、观察归纳、言语表达等活动,从而提高从数学角度发现和提出问题的能力、分析和解决问题的能力[1].

2.2 基于四基设计过程

依据高中数学课程理念,实现“人人能获得良好的数学教育,不同的人在数学上得到不同发展”[1],促使让学生感受新概念产生的必要性是非常重要的,故本节课主要从现实生活中的向量物理意义和类比数的加法使学生感知向量加法定义产生的必要性.并且概念应用环节,又让数学服务于现实世界,

高中生数学核心素养已逐渐显现出来,应基于“四基”设计过程,从“数”与“形”两个方面,从特殊到一般,从具体到抽象,让学生参与概括,参与表达.让学生感受新概念产生的必要性,感受新概念的合理性,体验、感受向量加法的本质特征,以获得更多的活动体验,积累基本经验,有效地培养和发展数学核心素养.

2.3 基于认知设计探究

如何使学生更加自然、更加直观深入地学习和掌握向量加法的本质,这就要求教师应设置一个更要符合学生认知规律的过程.

应基于“认知”提出问题,如“像位移合成的三个向量构成一个什么图形?从三个向量关系看,你得到什么结论?”,“如果向量a,b共线,它们的加法和数的加法有什么关系?你能作出向量a+b吗?”等等,这样更能接近学生思维的最近发展区.