基于非概率理论的引信MEMS安全与解除隔离装置闭锁机构可靠性评估

潘黎成,曹 云,2,雷胜洪,陆海宁,聂伟荣,席占稳

(1.南京理工大学机械工程学院,江苏 南京 210094;2.重庆长安工业(集团)有限责任公司,重庆 401120)

0 引言

微机电系统(micro-electromechanical system,MEMS)技术是提升武器性能和降低成本最有效、最有发展前途的技术之一,美国国防部于1995年将MEMS技术在引信安全系统中的应用列为12项国防应用之首[1]。文献[2—3]采用UV-LIGA工艺进行模块化设计,研制出适用于25 mm高爆榴弹、20 mm空爆弹等中小口径弹药的MEMS引信安全与解除偏离装置;文献[4]设计制作了碳化钨球驱动的MEMS安全与解除隔离装置。当前对引信MEMS安全系统的研究已取得了较多成果,但就整体而言尚未能够实现MEMS产品广泛应用,可靠性问题成为制约其发展的关键因素[5]。

引信作为弹药的关键部件,其可靠性和安全性直接影响战斗部的毁伤效能。可靠性是指器件在规定时间内、规定条件下完成预定功能的能力,可靠度是可靠性的概率度量[6]。对引信小子样可靠性评估已有相关研究,由于相关项目均涉及军事机密,最新的前沿理论很难发现,从公开的研究结果来看主要分为三个方面:1) 贝叶斯方法与多源信息融合;2) 自主方法与系统仿真;3) 可靠性多级综合方法[7]。三种方法均是采用场外同类样本的实验数据、仿真数据作为评估对象实验数据的补充,而后采用概率方法进行系统可靠性的评估,其核心思想是贝叶斯理论。采用非现场实验数据作为先验信息,从一定程度上可以弥补实验数据的不足。然而在很多时候尤其是军工领域同类样本的实验数据获得并不容易,而为了模拟真实的发射环境,进行仿真所耗费的计算资源和时间成本也很高,这就导致实验数据从根本上来讲比较贫乏。

采用概率可靠性评估方法进行分析需要大量的统计数据,当样本不足时所得统计参数不足以精确描述结构特征的分布规律[8]。已有研究结果表明,在概率模型中某一系统的可靠度对于不确定参数所对应的统计参数的微小误差非常敏感,设计不确定性的主观假设可能会导致结构可靠性分析出现严重错误[9]。文献[10—11]于1994首次提出一种用于描述不确定外界载荷或不确定几何误差所导致的器件失效的非概率凸模型,认为如果一个系统在发生故障之前所能容忍的不确定参数的波动幅度越大,那么该系统就越可靠。

目前,已有不少采用非概率理论进行可靠性分析的案例,取得了不错的效果:文献[12]采用非概率模型对飞机襟翼机构不对称运动的安全性进行分析,该方法可以合理地评估系统的可靠性;文献[13]采用区间非概率可靠性分析方法对复合材料高速转筒在长期高载荷下的运动可靠性进行评估,在缺乏实验数据或者仅能确定不确定参数变化区间时,可采用非概率可靠性评估方法,或者用该方法对概率可靠性方法进行有益的补充;文献[14]针对履带起重机工程实际中样本量较小的问题,采用非概率理论建立臂架结构非概率可靠性模型;文献[15]提出一种新的非概率时变可靠性模型,该模型可用于评估机构的运动可靠性;文献[16]将响应面方法和非概率凸模型相结合,提出了一种可应用于复杂工程问题的结构可靠性分析方法。综上所述,当样本量不充分时,可考虑采用非概率理论对系统进行可靠性评估。

针对小样本条件下传统评估手段计算精度差的问题,本文基于非概率理论,提出引信MEMS安解装置闭锁机构的可靠性评估方法,并且结合薄板理论建立闭锁机构区间非概率可靠性模型,得出非概率可靠性指标,之后进行区间变量的敏感性分析。

1 非概率理论简述

在大多数情况下,不确定参数(如载荷、结构尺寸等)精确的统计规律是不易得到的,但是不确定参数波动变化的范围是易于获得的,由此引出区间理论。

若结构的不确定参数x在某区间范围内变化,上界和下界分别为xu,xl,则x∈[xl,xu]属于区间变量,对应的区间中点xc和区间半径xr为

对区间变量x作标准化处理

x=xc+xrδ,

(2)

式(2)中,δ为标准化区间,δ∈[-1,1]。

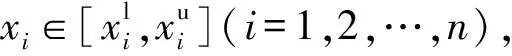
Z=g(X)=g(x1,x2,…xn)=
g(xr1,…,xro)-g(xs1,…,xsp)=
G(δr1,…,δro)-G(δs1,…,δsp),

(3)

式(3)中,g(X)为结构的功能函数在原始空间的表达;G(δ)为结构的功能函数在标准化区间内的表达形式;Xr={xr1,…,xro},δr={δr1,…,δro}为描述结构抵抗能力的不确定参数的区间变量;Xs={xs1,…,xsp},δs={δs1,…,δsp}为描述结构在外界载荷下响应的不确定参数的区间变量。

根据结构可靠性理论,当结构处于极限状态时,失效面g(X)=0将结构区间变量空间分割为两个部分,安全域g(X)>0和失效域g(X)<0。

文献[17]指出,对于任意连续的功能函数Z=g(X)=g(x1,x2,…,xn),在标准化区间变量的拓展空间中,基于区间模型的非概率可靠性指标定义为按无穷范数‖·‖∞度量的从坐标原点到失效面的最短距离:

η=min(‖δ‖∞)。

(4)

文献[18]已经证明对于线性功能函数,最可能失效点δ=(δ1,δ2,…,δn)位于标准化区间扩展空间内的对角线与失效面的某一交点上,满足

η=|δ1|=|δ2|=…=|δn|。

(5)

以二维线性功能函数为例说明可靠性指标的含义,如图1所示。

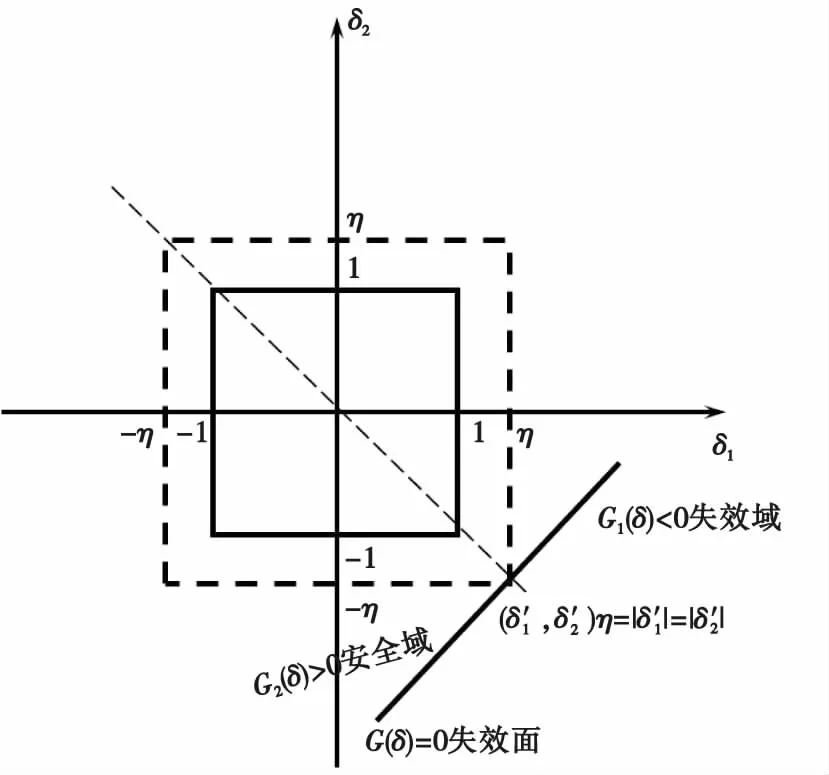
图1 二维线性功能函数非概率可靠性指标Fig.1 Two-dimensional linear functional function non-probability reliability index

而对于非线性功能函数,可靠性指标的求解则转化为如下的最优化问题:

以二维非线性功能函数为例进行说明,如图2所示。

图2中所示两个极限状态函数G1(δ)=0,G2(δ)=0,与线性功能函数不同的是,最可能失效点不一定位于角点,有可能位于极限状态函数的某一切点,如图所示最可能失效点分别为A、B,相应的可靠性指标为A、B坐标分量的最大值。

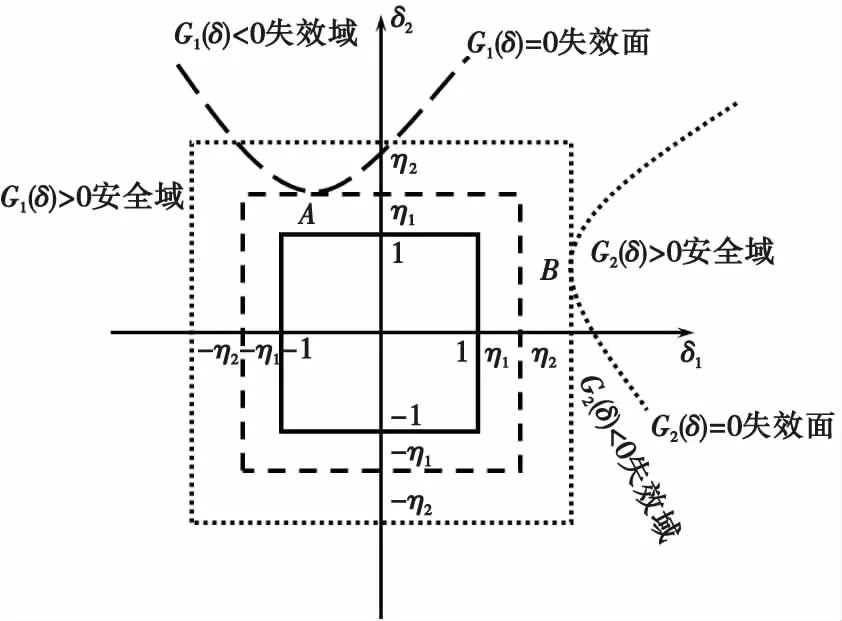
图2 二维非线性功能函数非概率可靠性指标Fig.2 Two-dimensional nonlinear functional function non-probability reliability index

2 闭锁机构可靠性模型

2.1 MEMS安全与解除隔离装置整体方案

本文所研究的MEMS安全与解除隔离装置适用于中大口径榴弹弹丸。其发射环境主要分为加速度幅值12 000g、脉宽为4～6 ms的后坐环境以及出炮口转速为ω=9 000 r/min的离心环境。其结构如图3所示。

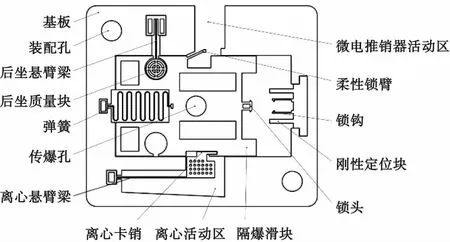
图3 MEMS安解装置整体示意图Fig.3 Overall schematic diagram of MEMS S&A device

MEMS安全与解除隔离装置主要由后坐保险机构、离心保险机构、指令锁保险机构、隔爆滑块以及闭锁机构组成。MEMS安全与解除隔离装置垂直弹轴安装,当弹丸正常发射时,后坐保险机构向下运动解除第一道保险;同时在离心载荷的作用下,隔爆滑块向右运动解除与离心悬臂梁的互锁,离心保险机构在离心载荷的作用下解除第二道保险;此后隔爆滑块继续向右运动直至锁钩紧密抵住基板,当弹丸飞行至预期地点时指令锁锁钩被微电推销打弯,解除对隔爆滑块的第三道保险;由于离心载荷的持续作用,隔爆滑块继续向右运动,带动锁头撑开锁钩并且锁定,隔爆滑块运动到位,此时传爆序列对正,引信完全解除保险,弹丸处于待发状态。

由MEMS安全与解除隔离装置运动原理可以看出,闭锁机构的可靠性直接影响引信的传爆序列在工作环境下能否可靠对正。若结构设计有缺陷,导致传爆序列无法对正或者重合度不足会影响弹丸的毁伤效能,因此有必要对闭锁机构的可靠性进行评估。

隔爆滑块在离心载荷的作用下向右运动撑开锁钩的过程中,锁钩可能存在两种失效模式:1) 闭锁机构尺寸、结构等设计不合理,在离心载荷下锁钩无法撑开,无法完成“闭锁”这一功能,称为“功能失效”;2) 锁钩被撑开,完成了“闭锁”这一功能,但此时锁钩已经屈服,发生塑性变形,这可能会导致传爆序列无法对正,称为“强度失效”。当器件的强度和功能均满足要求时才认为结构是可靠的。

2.2 闭锁机构强度可靠性

MEMS安全与解除隔离装置闭锁机构的强度可靠性指:滑块在离心力作用下运动,带动锁头撑开锁钩至最大限度时,锁钩不会发生屈服,此时认为该结构强度是可靠的。锁钩的设计尺寸如表1所示,其示意结构如图4所示。根据弹性理论,两个平行面和垂直于这两个平行面的的柱面所围成的物体称为板。如果板的高度H小于B/8～B/5,可以将其称为薄板[19]。所研究的锁钩其特征尺寸的比值为H/B=0.15,可近似为薄板。因此,锁钩内部应力状态可以采用薄板理论进行分析。

表1 锁钩结构尺寸设计值Tab.1 Design values of locking hook structure size

2.2.1问题简化

为了求解锁钩根部表面处的应力状态,同时为简化计算流程,先将该三维应力问题转化为平面应变问题得出其在Z和X方向的位移,再按照薄板理论得出应力。锁头撑开锁钩的过程,可以看作是锁钩端部受到方向向上的均布荷载(另一个锁钩受力相反)。由于荷载不随着Y方向发生变化,每个横截面的位移是相同的,因此可以通过单位宽度横截面的位移来近似计算锁钩的位移,从而求解应力。图5所示为抽取出的横截面。

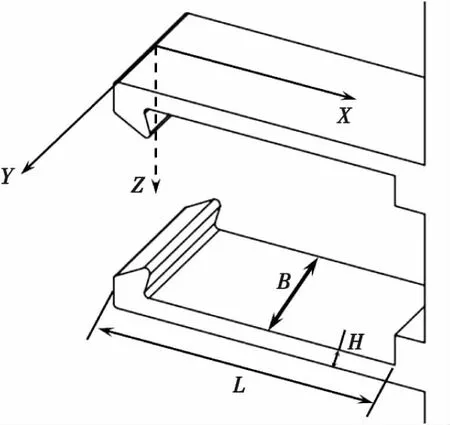
图4 锁钩示意图Fig.4 Schematic diagram of the flexible locking arm

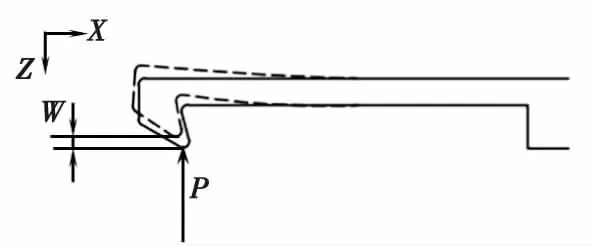
图5 抽取出的横截面Fig.5 Cross section

该单位宽度的锁钩由于被锁头挤压而张开的位移为W,可以看作是在载荷P的作用下,端部最大位移为W。因此锁钩被撑开的过程转化为锁钩端部在载荷P的作用沿Z方向位移W,求解此边界条件下内部的应力。根据圣维南原理,在面力等效的情况下,远处所受的影响可以忽略不计,锁钩根部处应力状态不会发生太大改变,因此可将抽取的模型进一步简化为一个悬臂梁,如图6所示。

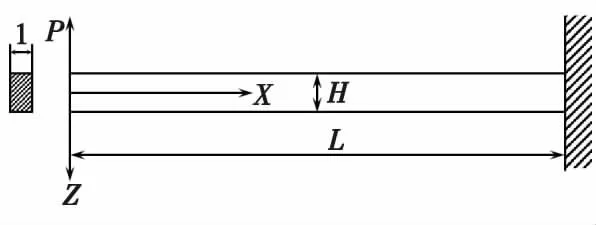
图6 横截面简化为悬臂梁Fig.6 Cross-section simplified to cantilever beam

2.2.2应力求解

按照平面应变问题,求解悬臂梁的位移。选取二次应力函数和四次应力函数[20]:

根据材料力学基本假设,梁Z方向挤压应力忽略不计,即σz=0。取二次应力函数为均匀剪应力荷载,即c2=0,a2=0,采用叠加原理,将二次应力函数所对应载荷与四次应力函数适当结合可得平面问题下各应力分量分别为

边界条件为

(10)

因此得到平面问题下各应力分量和应变分量为

得到平面问题下梁上各点Z方向的位移为

根据前文弹性理论的假设,在Y方向上各个横截面的位移均是相同的,薄板位移与y坐标无关,且根据板壳理论,在中面的任一根法线上,薄板沿厚度方向所有各点均具有相同的位移w,薄板上沿厚度方向各点的位移可由挠度近似为

应力分量τzx,τzy,σz远小于其余三个应力分量,其对应的应变可以忽略不计。可得到锁钩根部表面处应力为

根据式(16)可求得各主应力如式(17)所示。

式(17)中,P为锁梁端部荷载,P=3EI1W/L3。

梁根部表面处的等效Von-Mises应力为

式(18)中,μ、E分别为电铸镍泊松比以及弹性模量,W、H、L分别为锁钩载荷端Z方向位移、锁钩厚度以及其长度。

因此强度可靠性的功能函数为

式(19)中,σs、ns分别为电铸镍的屈服强度和安全系数,ns=1.2。

2.3 闭锁机构功能可靠性

根据能量守恒原理,离心力对滑块所做功转化为弹簧的弹性势能、锁钩应变能以及滑块的动能,如果在离心载荷的作用下滑块运动到闭锁梁张开的极限位置时其动能仍然大于0,表明离心载荷仍有余能为滑块提供动力,促使滑块经过锁钩,该结构的功能可靠性达到要求。

设炮弹出膛口转速为ω,离心力对隔爆滑块所做功为

(20)

式(20)中,m为隔爆滑块的质量,ω为炮弹出膛口转速,d为静止时隔爆滑块质心与炮弹转轴的距离,D为闭锁后质心与转轴的距离。

微弹簧的弹性势能为

式(21)中,k为微弹簧刚度。

在薄板的小挠度弯曲问题中,不计应变分量εz,γyz,γxz,因此弹性体的应变能为

(22)

得到

式(23)中,B为锁梁的宽度,其余各个参数与式(18)内的参数含义一样。

因此功能可靠性的功能函数为

g2=QFω-Qs-Vε。

(24)

2.4 可靠性指标求解

采用光学显微镜对一批样件共10个样本的闭锁机构关键部件进行拍摄,然后测量。由于显微镜视场较小,无法将锁钩完全拍下,因此分为两次拍摄,之后采用SIFT算法对其进行拼接。图7所示为某样本的一对锁钩。

图7 光学显微镜拍摄的锁钩Fig.7 Locking hooks photographed by optical microscope

文献[21]对电铸镍膜进行拉伸实验,获得其弹性模量E和屈服极限σs。采用图像处理软件ImageJ对锁钩长度L和锁钩厚度H进行测量。对于同一批样件而言,UV-LIGA工艺使用同一块晶圆生产,锁钩宽度B可认为是不变的。锁钩的结构和材料参数如表2所示。

根据表2将功能函数g1、g2进行标准化,如下所示:

式(25)中,E=82+3δE,W=111.95+10.54δW,H=120.105+5.325δH,L=1 870.21+53.35δL。

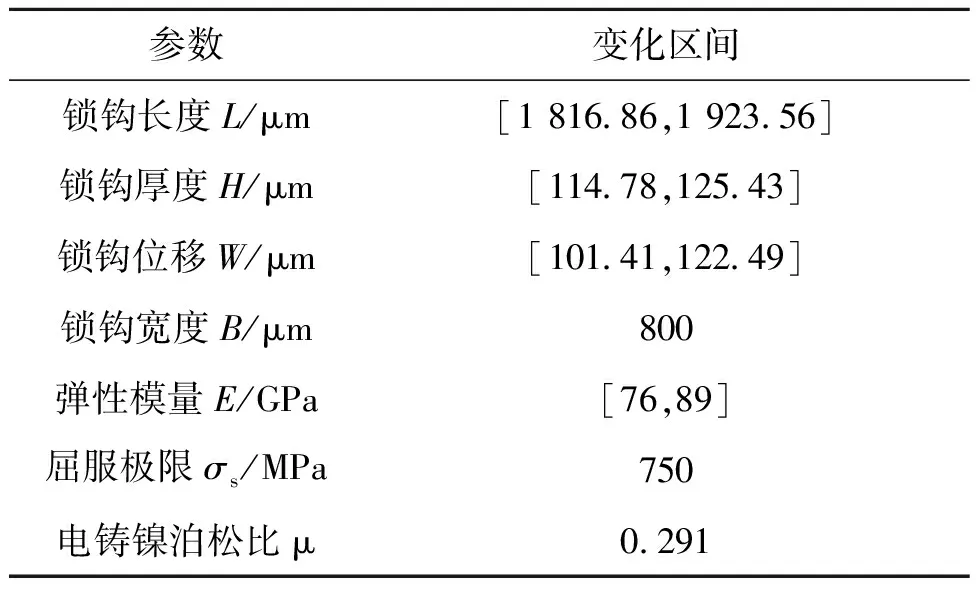
表2 锁钩参数及其变化区间Tab.2 Locking arm parameters and their variation intervals

根据非概率可靠性指标定义,非概率可靠性指标η的求解可以转换为如下的最优化问题:

文献[22]指出工程实际中功能函数的响应可能非常复杂,如果采用梯度迭代的方法可能会得到不准确的可靠性指标,采用帝国竞争算法(ICA)可以不用考虑复杂功能函数的梯度,之后的数值算例也证明ICA与遗传算法、粒子群算法相比结果更优。因此本文也采用ICA,得出非概率可靠性指标为η1=1.577 6>1,η2=18.034 2>1。根据非概率可靠性指标的含义,η1表明在这一批样本下,锁钩强度可靠性极限状态函数远离变量区间,在张开的过程中锁钩内最大应力始终小于电铸镍屈服极限,该闭锁机构在运动过程不会发生塑性变形;η2则表明功能可靠性极限状态函数远离变量区间,离心载荷对隔爆滑块所做的功在转化为弹簧的弹性势能以及锁钩的应变能后,仍然留有很大余量作为隔爆滑块的动能,促使滑块通过锁钩。综合上述,仅从数学意义上而言,两种非概率可靠性指标表明,当锁钩的结构参数在如表1所示的变量区间内变动时可以实现可靠闭锁,其功能是可靠的。

2.5 区间变量的敏感性分析

根据非概率可靠性分析方法得出了引信MEMS安全与解除隔离装置闭锁机构的可靠性指标之后,可根据该指标初步了解到所设计的结构的可靠程度。但是如何根据可靠性指标来指导后续的优化设计,还需要对区间变量进行敏感性分析,从而定量判断出设计参数在区间内变化时对于结构响应的影响程度[23]。对于区间变量来说可采用区间敏感性分析方法。把表征不确定性的区间敏感性因子[24]定义为

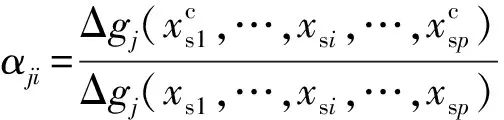
(26)

区间敏感性分析所表达的是设计变量区间的变化程度对结构响应区间的影响程度。|αji|越大,表明第j个结构响应对于第i个不确定参数的敏感性就越强,反之则越弱。通过闭锁机构的强度可靠性功能函数以及功能可靠性功能函数,结合区间敏感性因子,可以定量判断出当不确定参数在区间内波动时对闭锁机构的结构响应(应力、能量)的影响程度。

对不同量纲的不确定参数进行敏感性分析时须先进行量纲统一或者对参数进行一定的转化[27]。引入一个中间变量:变异系数,用于表征不确定参数的波动变化范围,同时对参数进行量纲统一。与概率论中的变异系数CV相类似, CV越小,表明不确定参数波动变化范围越小,越接近中值。变异系数可以表示为

通过对闭锁机构2种失效模式下区间敏感因子的计算,给出了不确定参数的变异系数在0.01～0.8之间的结构响应敏感因子的变化曲线,如图8和图9所示。

图8 应力敏感因子随变异系数的变化曲线Fig.8 Variation curve of stress sensitivity factor with coefficient of coefficient of variation

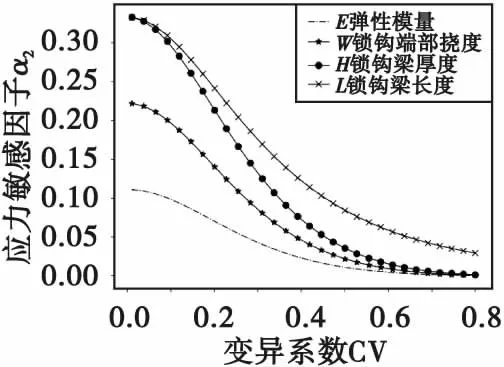
图9 能量敏感因子随变异系数的变化曲线Fig.9 Variation curve of energy sensitivity factor with coefficient of coefficient of variation

由图8—图9可以看出随着变异系数的增加,各个不确定参数对于结构响应的影响逐渐变弱,即随着不确定参数区间的逐步扩张,单个不确定参数对于结构响应的影响越来越小,此时需要综合考虑多个不确定参数对结构的影响。

图8中,不确定参数弹性模量E,锁钩端部挠度W以及锁钩梁厚度H的应力敏感因子α1之间的关系为α1E≈α1W≈α1H≪α1L。

弹性模量、锁钩端部挠度以及锁钩梁厚度这3个参数对于结构响应的影响相当,而这3个参数应力敏感因子远小于锁钩梁长度的应力敏感因子,并且随着变异系数的增加,α1E、α1W、α1H趋近于0,表明此时这3个不确定参数对于结构的影响微乎其微。

图9中,各不确定参数的能量敏感因子α2之间的关系为α2E<α2W<α2H<α2L。

弹性模量、锁钩端部挠度、锁钩梁厚度和锁钩梁长度这4个参数对于结构响应的影响逐步增加,并且随着变异系数的增加,α1E、α1W、α1H趋近于0。

综上所述,对于结构的设计优化应该这样考虑,若引信MEMS产品生产制造时的工艺误差较小,即变异系数较小时,E、W、H、L这4个不确定参数均对结构有较大的影响,但是不论从应力角度还是能量角度锁钩梁长度L对于结构响应的影响最大,在设计优化时应该优先考虑,之后考虑另外3个参数;若引信MEMS产品生产制造的工艺误差很大,即变异系数很大时,图中可以看出E、W、H对于结构的影响微乎其微,L占据主导地位,此时主要考虑锁钩梁长度L。

但是在实际生产过程中不会有这么大的工艺误差,结合表1可知变异系数最大为0.094 1,现假设工艺误差较大的情况:将变异系数放宽至0.15。综合考虑图8和图9可以得知在对引信MEMS安解装置闭锁机构进行设计优化时优先考虑锁钩梁长度L以及锁钩梁厚度H,辅助以弹性模量E、锁钩端部挠度W比较合适。

3 闭锁机构可靠性测试及分析

3.1 离心实验

采用离心实验平台对2.4节中测量的10个样本进行离心闭锁实验,验证10个样本闭锁机构的可靠性。由于引信在炮弹上真实的安装位置距离转轴很近,转盘无法达到相同的安装条件,因此将MEMS安解装置偏置一段距离r,根据离心转盘的转速和偏置的距离来获得等效转速,进而模拟炮弹发射时的离心环境。

基于离心旋转台进行离心实验平台的搭建,实验平台如图10所示,已装配样机的夹具通过螺钉安装在离心转盘上,安装时将离心转盘半径与样机对称中心线保持一致。

图10 离心实验平台Fig.10 Centrifugal experimental platform

根据转盘转速,可得隔爆滑块所受的离心加速度为

式(28)中,n为离心转盘的转速,r为隔爆滑块质心相对于离心转盘圆心的距离,本次实验选取r=57 mm。

由于MEMS器件存在生产误差,每一个样本的特征尺寸与设计值存在误差,每一个样本的闭锁情况都不相同。为了确定每一个样本的闭锁机构从未能闭锁至闭锁的临界转速,针对实验样本,每次实验只取一个样本安装于离心实验平台。实验初始施加2 700 r/min的转速,观察到隔爆滑块锁头运动并顶住了锁梁,但是并未闭锁。此后对转盘依次增大50 r/min转速,观察其闭锁情况。闭锁机构离心实验后状态如图11所示,实验结果如表3所示。

图11 离心实验后闭锁机构状态Fig.11 Status of latching mechanism after centrifugal experiment

3.2 实验结果分析

实验结果表明,MEMS安全与解除隔离装置闭锁机构在平均等效转速10 309 r/min时能实现可靠闭锁,表现出良好的闭锁一致性,这一结果与预期的出膛口转速在9 000 r/min以上的设计目标相符合,并且在闭锁成功后柔性锁梁没有发生塑性变形。这一批样本均能实现可靠闭锁,这与非概率可靠性理论所评估出的结果一致,表明了采用非概率可靠性理论对MEMS安全与解除隔离装置闭锁机构进行可靠性评估的有效性。

4 结论

本文将MEMS安全与解除隔离装置的不确定参数看作是区间变量,采用非概率理论对MEMS安全与解除隔离装置闭锁机构进行可靠性评估,建立闭锁机构区间非概率可靠性模型。该方法从一定程度上弥补了工程实际中MEMS安全与解除隔离装置样本量稀少,概率可靠性模型难以建立的缺陷。之后将可靠性指标的求解转化为一个最优化问题得出其指标,并且进行区间变量的敏感性分析。最后进行离心实验模拟炮弹发射时的离心环境,实验结果与非概率可靠性理论评估的结果具有很高的一致性,表明非概率理论对MEMS安全与解除隔离装置可靠性评估具有较好的适应性,可为后续的引信MEMS安全与解除隔离装置可靠性分析提供参考。