绳驱动万向关节的绑线机构优化

陈正隆,李同杰,李晓贞

(安徽科技学院 机械工程学院,安徽 凤阳 233100)

随着科学技术的发展,仿生学和智能机器人技术越发成熟,关节作为机器人运动的重要部件,结构和尺寸越来越精密,由仿生学引起的机器人热点分类——柔性机器人,被学术界视为最有可能的新一代机器人发展方向[1-2]。传统关节主要是以刚性结构为主,灵活性、安全性较差,基于此原因人们开始研究具有弯曲性、灵活性的关节,并将这类关节称为柔性关节[3-4]。

柔性关节广泛地在工业、医疗等各个领域内应用,驱动绳和形状记忆合金是目前广泛采用小型柔性关节驱动方式[5]。Dong等[6]已研制一种由3根柔性的绳索来驱动关节运动的蛇形臂机器人;李法民等[7]利用指数积(POE)公式建立绳驱动机器人的运动学模型;薛赞等[8]提出一种具有更强环境适应性、更高自由度和更大工作空间的冗绳驱动机械臂。在形状记忆合金方面,王鲁炳等[9]基于形状记忆合金丝设计了一种多关节可弯曲柔性机械臂。形状记忆合金由于制造复杂、安装要求高,所以在工程化开发中一般使用绳驱动作为小型柔性关节驱动方式[10-11]。

绳驱动的结构原理是将驱动绳的一端固定在绑线机构上,另一端固定在运动机构上,并在二者之间设置驱动绳的限位通道,限位通道使得驱动绳按照设定的方向运动;通过绑线机构的运动,带动驱动绳在限位通道中的运动,驱动绳在绑线机构中的绳长发生变化,从而使得运动机构中的驱动绳绳长发生变化,进而带动运动机构发生运动。绕圆运动的特性导致绑线机构在弯曲运动时内侧和外侧的驱动绳长的变化值不同,使得运动机构中对应绑线机构的弯曲内外侧的驱动绳长变化值也不同,即弯曲一侧的驱动绳绷紧,另一侧放松,导致绑线机构和运动机构存在运动不同步的情况[12-13]。因此,需要对绑线机构进行设计优化,使用三维软件建数学模型,Matlab软件进行数值模拟等方法来分析模型[14],旨在减少绑线机构造成的驱动绳绳长变化差值,提高运动的同步性。

绳驱动作为小型柔性关节的一种驱动方式,应用的结构中柔性关节的直径普遍小于20 mm,由于结构的设计,驱动绳直径选择在1 mm以下,应用的结构受力不超过50 N,已知直径0.3 mm的尼龙线拉力为187 N,远远超出结构最大受力,产生的拉伸变形可以忽略不计;由于运动机构的运动方向是由若干个限位通道的轴线方向拟合而成的弧线,驱动绳安装在限位通道中,运动方向沿着限位通道的轴线方向前后运动,驱动绳对限位通道壁的压力可以忽略,即忽略摩擦力。本研究在模型的建立和计算结果的分析中均设为理想状态下,不考虑驱动绳拉伸变形和驱动绳与绑线结构之间摩擦的情况。

1 绳驱动万向关节绑线机构数学模型的建立

1.1 绑线机构的三维模型

绑线机构由1个二自由度球关节作为主要部分,如图1所示,为限制三自由度球关节的自由度,球关节底座上的球体单方向在径向处设有凹槽让位腔,球关节摇杆上的外球体相对应位置处设有凸台限位块[15-17];球关节底座运动时固定,球关节摇杆在平面两方向上自由运动,叠加形成万向运动,控制万向关节的万向运动;万向关节一般由4根驱动绳控制,驱动绳的穿线点分布在万向关节圆截面上,4个穿线点均分由穿线点到关节圆心为半径的圆,1组穿线点之间的连线经过凹槽让位腔和凸台限位块的对称中心;轴截面上的2根驱动绳为1组控制1个方向,球关节摇杆单向运动时,同组的2根驱动绳同步运动,处于万向关节弯曲内侧的绳子收紧变短,弯曲外侧的绳子放松变长,使得万向关节同步弯曲。球关节因为凹槽让位腔和凸台限位块的存在不发生相对自转,不打乱驱动绳的分布;凹槽让位腔和凸台限位块使得球关节在万向运动时2个方向上的运动轨迹并不相同,2组驱动绳绳长的变化也不同,因此建立数学模型时将2组驱动绳分别计算分析。

图1 绑线机构三维模型Fig.1 Three-dimensional model of the wire tying mechanism

1.2 绑线机构的数学模型

1.2.1 三维模型简化 将绑线机构的三维模型进行分析、简化,简化后的模型如图2所示,三维模型中绳长转换成简化模型中2点之间的距离,数学模型中体现为距离的数值大小。简化后的绑线机构模型由绑线球、限位圆盘、驱动线组成,绑线球是半径为r的球体,位于XaYaZa坐标系中,球心为XaYaZa坐标系原点,原模型中凹槽让位腔和凸台限位块位于XaZa平面。XaYa平面圆周均分设4个绑线点A1、B1、C1、D1。绑线球正下方放置1个限位圆盘,圆盘的半径为R,圆盘的圆心和球体的球心的距离为L,设圆盘平面为XY平面,限位圆盘指向绑线球的方向为Z轴正方向,XY平面上圆周均分4个出线点A、B、C、D。在XaYaZa坐标系的坐标为：A(0,-R,-L)、B(R,0,-L)、C(0,R,-L)、D(-R,0,-L)。XaYaZa坐标系经过绕Ya轴和Xb轴分别旋转α度和β度后变换为XbYbZb坐标系、XcYcZc坐标系,绑线点A1在旋转后为点A2、A3,B1、C1、D1点同理。驱动绳为连接对应绑线点和出线点之间的线段,根据角度变换导致驱动绳绳长的变化。将驱动绳分为BD侧驱动绳和AC侧驱动绳：B和D点的驱动绳经过1次角度的变化,控制1个方向的运动且位于同一轴截面上;A和C点的驱动绳经过2次角度的变化,控制1个方向的运动且位于同一轴截面上。

图2 简化后的绑线机构模型Fig.2 Simplified model of the wire tying mechanism

1.2.2 数学模型建立 使用旋转矩阵求A3点在XaYaZa坐标系的坐标：A3点在XcYcZc坐标系中的坐标为(0,-r,0),首先通过绕Xc轴旋转β度得到XbYbZb坐标系,其次通过Yb轴旋转α度得到XaYaZa坐标系;用齐次方程法将A3点在XcYcZc坐标系中的坐标转换成(0,-r,0,1),写成矩阵的格式。

(1)

XcYcZc坐标系绕Xc轴旋转β度得到A3点在XbYbZb坐标系中的坐标：

A3b=RX×A3

(2)

XbYbZb坐标系绕Yb轴旋转α度得到A3点在XaYaZa坐标系中的坐标：

A3a=RY×A3b

(3)

联立式(2)～(3)得：

A3a=RY×RX×A3=R×A3

(4)

总的旋转矩阵R：

(5)

联立式(1)、(4)、(5)得：

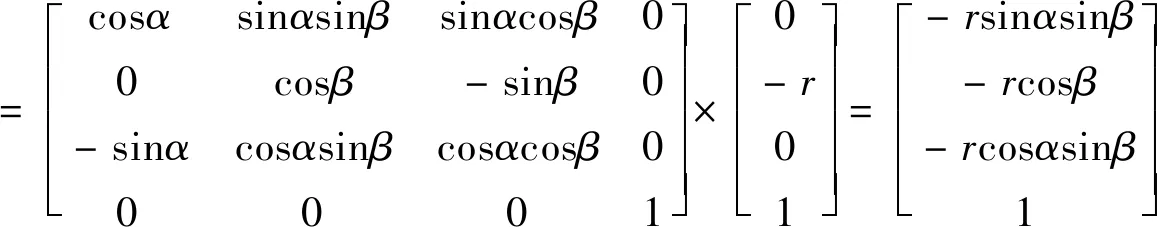
(6)

即A3点在XaYaZa坐标系中的坐标：

A3：(-rsinαsinβ,-rcosβ,-rcosαsinβ)

同理可得B1、C1、D1等3点在经过旋转变换后的B3、C3、D3等3点的坐标：

B3：(rcosα,0,-rsinα)

C3：(rsinαsinβ,rcosβ,rcosαsinβ)

D3：(-rcosα,0,rsinα)

三维坐标系中两点之间的距离公式：

(7)

将得到的4个点的坐标带入式(7),得到经过旋转变换后4个绑线点对应圆盘出线点的距离：

(8)

(9)

(10)

(11)

联合式(8)、(10)得到AC侧2根驱动绳绳长变化值的差值：

(12)

联合式(9)、(11)得到BD侧2根驱动绳绳长变化值的差值：

(13)

2 数字模型计算分析

分析数学模型发现同组驱动绳绳长的差值只和绑线球半径r、限位圆盘半径R和绑线球球心与限位圆盘圆心之间的距离L相关,原模型中绑线球半径r和限位圆盘半径R相等,绑线球球心与限位圆盘圆心之间的距离L在不同应用结构中变化,将数学模型导入Matlab软件中进行数值分析计算,计算2组驱动绳在不同的绑线球半径r、限位圆盘半径R和绑线球球心与限位圆盘圆心之间的距离L之间的关系导致的驱动绳绳长差值大小。绑线球半径设为r=50,旋转角度α和β设为0°～30°。

2.1 BD侧驱动绳绳长差值

BD侧驱动绳绳长经过1次旋转变换,设限位圆盘半径R和距离L为绑线球半径r的倍数来进行数值分析。

2.1.1 原模型绳长差值 原绑线机构模型中限位圆盘半径R等于绑线球半径r,取不同长度的距离L,得到BD侧绳长差值与角度的折线图。由图3可知,限位圆盘半径R等于绑线球半径r时,在同一根折线上α=30°时差值最大,随着距离L的不断增大,驱动绳绳长的差值越来越小,但折线的变化趋势不变,表示距离L不是影响结果的主要参数。

图3 R=r时BD侧驱动绳绳长变化Fig.3 Change of BD side drive rope length when R=r

2.1.2 优化模型绳长差值 距离L不是影响驱动绳绳长差值变化趋势的主要参数,因此取不同的限位圆盘半径R值来分析计算结果的变化趋势,取限位圆盘半径R等于1.2r和0.8r时,得到差值折线图。由图4可知,同根折线上在α=30°时差值最大;由图4(a)可以明显发现在R=1.2r时,绳长差值的变化明显的提高了2倍以上;由图4(b)可知当限位圆盘半径R等于0.8r时,绳长的差值变成了负值,但绳长差值极值的绝对值与原模型接近。结合图3～4中折线的发展趋势和数值大小分析易知：在限位圆盘半径R的值(0.8～1)r,BD侧驱动绳绳长变化的差值从正值变为负值且绝对值接近,表明当R取值范围在此区间内时,模型的BD侧驱动绳绳长变化的差值小于原模型。该取值范围减小了绳长差值,优化了万向关节运动的同步性。

图4 R=1.2r和R=0.8r时BD侧驱动绳绳长变化Fig.4 Change of BD side drive rope length when R=1.2r and R=0.8r

2.1.3 二次优化模型绳长差值 为进一步优化绳长的差值,将特定参数带入数学模型,反求出R和r的关系。将L=r、α=30°带入模型中得到折线图(图5),当R和r的比值在0.9～0.95时,差值存在零点;将差值0带入图5,得到R=0.928r。将该参数下的模型进行数值分析,得到差值的折线图(图6)。由图3～6和表1可知,影响计算结果变化趋势的主要参数是限位圆盘半径R和绑线球半径r的比值;当R=0.928r时,BD侧绳长变化的差值明显小于其他情况,也验证了优化的限位圆盘半径R的取值范围。

图5 30°时差值随R与r比值变化Fig.5 Variation of the difference with the ratio of R to r at 30°

图6 R=0.928r时BD侧驱动绳绳长变化Fig.6 Variation of BD side drive rope length when R=0.928r

表1 不同R、L值下BD侧绳长差值的极值Table 1 Extreme values of rope length difference on BD side with different values of R and L

2.2 AC侧绳长差值

AC侧的驱动绳绳长经过2次角度的变换,由于距离L不是影响结构的主要参数,因此只取L=r的参数进行分析。

2.2.1 原模型绳长差值 取限位圆盘半径等于绑线球半径的情况,由图7可知,AC侧驱动绳绳长变化的差值因为经过2次变化,形成的变化图是曲面,随着α和β角度的变大而越来越大,差值的最大值在2个参数的最大值处。

2.2.2 优化模型绳长差值 取不同的取限位圆盘半径R来分析结果的变化趋势,由图8(a)发现,在R=1.2r时,AC侧绳长差值的变化趋势明显提高;由图8(b)、8(c)可知,当限位圆盘半径R小于绑线球半径r时,绳长的差值部分变成了负值,且绳长差值的极差小于原模型,在R=0.8r和R=0.928r时绳长差值的极差接近。结合图7～8和表2可知,AC侧驱动绳绳长变化差值的大小随着R的变大而变大,因此R的取值应该小于r,AC侧驱动绳分析结果验证了BD侧驱动绳分析的结果,反证了数学模型和数值模拟的合理性。

图8 R=1.2r、R=0.8r和R=0.928r时AC侧驱动绳绳长变化Fig.8 Variation of AC side drive rope length when R=1.2r,R=0.8r and R=0.928r

表2 不同R值下AC侧绳长差值的极差Table 2 Polar difference of rope length difference on AC side with different R values

3 结论

本研究通过将绑线机构的三维模型简化后重建为数学模型,并对其进行了数值模拟计算,对计算结果进行分析研究从而优化模型,发现驱动绳绳长变化的差值只和绑线球半径r、限位圆盘半径R和绑线球球心与限位圆盘圆心之间的距离L相关。距离L只影响驱动绳绳长变化的差值数值大小,不影响变化趋势,因此不是主要参数。限位圆盘半径R的取值为(0.8～1)r时,BD侧驱动绳绳长变化的差值比原模型的差值小;在R=0.928r时差值最小。限位圆盘半径R的取值大于绑线球半径r时,AC侧驱动绳绳长变化的差值比原模型的差值大,且数值变化快、幅度大;限位圆盘半径R的取值小于绑线球半径r时,AC侧驱动绳绳长变化的差值比原模型的差值小,且数值变化慢、幅度慢。限位圆盘半径R为0.928r、距离L为机构允许的最大值时,绳长变化的差值最小,提高了万向关节运动的同步性,达到优化绑线结构的目的。