基于ACO-LEVY的小型无人直升机频域响应辨识方法

刘鑫瑜,周 健,卢 健,王 耿

(1.西安工程大学 电子信息学院, 西安 710048;2.西北工业大学 无人系统技术研究院, 西安 710072)

0 引言

小型无人直升机在多领域迅速发展,如搜索救援、地质勘探、物流输送、武器装载等。从民用到军用,小型无人直升机都受到广泛的重视[1-2]。由于小型直升无人机自身结构复杂、非线性、强耦合等特性,通过数学建模解决小型无人直升机建模问题往往显得力不从心,缺乏精确的动力学模型成为制约无人机直升机发展的重要因素。而系统辨识得益于以数据为驱动进行模型辨识,规避了系统结构复杂等特性,成为了小型无人直升机建模的主要研究方向。

随着傅里叶变换的引入,Tishcler将谱函数分析法应用于飞行器辨识中,为频域辨识在旋翼飞行器建模中建立了理论优势[3]。随后,Tishcler提出了一种基于复合分窗和规整谱量的频域辨识优化算法[4],获得了较为精确的频率响应曲线,使用该方法成功辨识了黑鹰直升机UH-60[5]、R44[6]、无飞杆旋翼机[7]以及倾转旋翼机XV-15悬停下和小速度前飞下的模型[8],标志着该方法在旋翼飞行器频域辨识的领先地位。在该方法的背景下,人们为提高所得到的动力学模型预测精度从诸多方面开展了研究。文献[9]中针对数据测量时所产生的误差,提出了一种飞行数据预处理方法,有效地提高了数据的质量。文献[10]中通过机理建模从而改进非线性模型结构。文献[11]中通过导出伯德灵敏度函数并结合机理模型分析得到辨识模型结构,提高了模型辨识精度。文献[12]中通过偏向干分析,消除了次要输入的线性影响,提高了频谱的精度。上述研究工作均在不同方面提高了模型的预测精度。

而针对频率响应曲线拟合问题,LEVY法作为一种线性最小二乘辨识算法,通过分离传递函数的实部及虚部求极值来拟合频域曲线,具有算法简单适应性强等特性[13],蚁群算法作为一种模拟自然界生物种群行为的仿生优化算法,相比于其他智能优化算法,蚁群算法动态搜索能力较强、具有记忆性、适用于多参数复杂性问题求解及优化[14]。

本文中提出了一种基于蚁群优化LEVY法参数(ACO-LEVY)的频域曲线拟合方法,通过机理分析对小型无人直升机进行模型建立,并以数据为驱动利用复合分窗以及偏相干的方法得到小型无人直升机的频域特性曲线,使用LEVY法拟合其频域特性曲线从而得到初始模型结构,之后利用蚁群算法动态搜索能力较强的特点对LEVY法中的参数进一步优化。最终的得到小型无人直升机横向、纵向通道的传递函数模型以及辨识参数结果。并在时域下验证模型预测的有效性以及准确性。

1 小型无人直升机数学模型建立

本文测试试验平台采用自主研制的Raptor-50型小型无人直升机,如图1所示。

图1 小型无人直升机Fig.1 Small unmanned helicopter

主旋翼垂直下方加装了一套Bell-Hiller稳定副翼起阻尼器的作用。在发动机工作时,主旋翼与桨毂共同旋转。本文采用叶素法对主旋翼以及稳定副翼进行气动分析[15],将稳定副翼看作为没有升力的旋翼平面,因此主旋翼以及稳定副翼挥舞方程表示为:

(1)

(2)

(3)

(4)

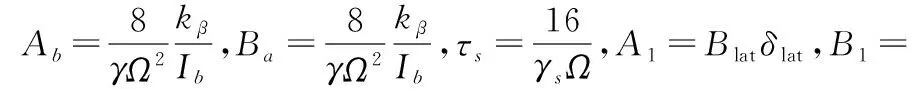
式中:τm和τs为主旋翼和副翼响应时间常数,a1和b1分别为主旋翼纵向、横向挥舞系数;c1和d1分别为副翼横向、纵向挥舞系数;A1和B1分别为主旋翼横向、纵向周期变距输入;C1和D1分别为主旋翼横向、纵向周期变距输入。

b1=-τmp+Bdd1+Blatδlat

(5)

将副翼横向通道的挥舞方程进行拉普拉斯变换得到:

τssd1(s)=-d1(s)-τsp(s)+Dlatδlat(s)

(6)

对式(6)整理得到副翼的传递函数为:

(7)

将式(7)代入式(5)中得到:

(8)

对式(7)进行拉普拉斯反变换并整理后得到横向角速率方程:

(9)

(10)

(11)

因小型无人直升机在采集数据中含有舵机动态特性,因此在模型建立时应将舵机动态特性融入传递函数模型中。本试验平台舵机可用二阶传递函数表示:

(12)

因此在考虑舵机的情况下,小型无人直升机横向、纵向通道的传递函数模型表示为:

(13)

(14)

式中:Ma1和Lb1、τsq和τsp分别为横向、纵向的主旋翼的挥舞力矩导数和副翼响应时间常数,以上4个参数未能通过理论计算得到,需要通过下文频域辨识的方法分析得到。

2 小型无人直升机频域辨识

2.1 基于加窗和偏向干的频率响应

为获得不同频率下的飞行数据,将扫频输入作为输入激励信号。本文采用Chirp-Z变换将时域数据变换为频域,减少数据截断所导致的功率谱泄露[16]。

为了降低随机误差对频谱估计的影响,提高自功率谱Gxx(f)和互功率谱Gxy(f)的准确性,采用复合加窗的方法,通过融合多个平滑窗口的结果来改进谱估计,复合加窗按照2∶1相互重叠[15]。谱估计的平滑结果是对每一个窗口中信号进行功率谱估计的平均:

(15)

(16)

针对不同宽度窗函数分别计算功率谱所产生的随机误差,采用误差权重公式:

(17)

(18)

由于小型无人直升机耦合程度高,是一个典型的多输入多输出系统,这里将其分解为多输入单输出系统来处理。为了消除影响辨识通道结果的次要输出,获得更加精确的结果,本文采用偏相干的方法[12]。这里以横向通道为例,δlat为横向输入,δlatc和δlatuc为与航向输入相关和不相关的输入,p为滚转角速率,如图2所示。

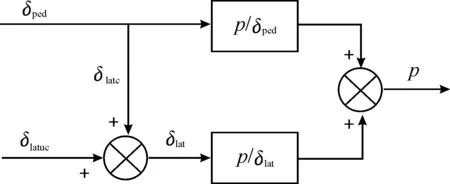
图2 双输入单输出系统结构Fig.2 Dual input with single output system structure

其中,主要输入δlat由与航向输入相关的δlatc和不相关的δlatuc组成:

δlat=δlatc+δlatuc

(19)

对于辨识通道p/δlat,消除次要输入δped所产生的线性影响δlatc后频谱表示为:

(20)

(21)

(22)

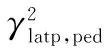
(23)

因此,得到p/δlat的频率响应为:

(24)

2.2 基于ACO-LEVY法模型辨识

通过上述方法获得小型无人直升机横向、纵向通道的频率响应曲线,本文采用LEVY法对频率响应曲线进行拟合,从而获得该方法的初始模型结构[17]。

小型无人直升机以频率ω为自变量的传递函数为:

(25)

通过使频率响应H(jω)和实验数据之间误差平方最小化,从而估算待定系数ai和bi。共测N个频率点,取ω=ω1,ω2,…,ωN。频率响应与所求传递函数误差为:

(26)

这里定义广义误差为ek:

ek=H(jωk)A(jωk)-B(jωk)=eik+ejk

(27)

将频率响应H(jω)以复数形式表示,则广义误差表示为:

(28)

将全部采样频率ωk的误差平方和定义为误差准则J:

(29)

令J对ai和bi分别求偏导,得到:

(30)

可以得到(n+m+1)个式子,定义以下元素:

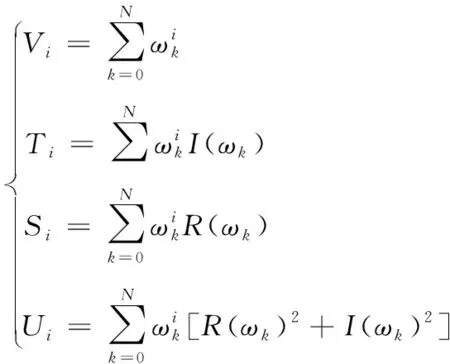
(31)

根据上文可知,本文采用的小型无人直升机传递函数模型可以看作一个四阶系统。设传递函数为:

(32)

对式(31)求解得到LEVY法初始模型结构:

(33)

蚁群算法动态搜索能力较强、具有记忆性、适用于多参数复杂性问题求解。为获得更加精确的传递函数模型,本文采用蚁群算法对式(33)中的Vi、Ti、Si和Ui参数进行优化,获得全局最佳位置即最优参数。计算全局最优参数时,需要将更新后的参数代入式(33)中从而得到新的传递函数,将传递函数预测结果的均方差作为适应度值,MSE计算公式为

(34)

式中:N为数据个数;f(xi)为模型预测数据;y(xi)为实际输出数据。

蚁群算法优化LEVY参数主要步骤为:

1) 初始化蚂蚁个数为m=50,最大迭代次数G=100,信息素蒸发系数Rh0=0.9,转移概率常数P0=0.2,局部搜索步长step=1 000,参数寻优范围x∈[0.8x,1.2x]。

2) 随机蚂蚁的初始位置,并根据式(33)得到传递函数,通过式(34)计算适应度函数值,设为初始信息素,并且计算状态转移概率。

3) 进行位置更新:当转移概率常数大于状态转移概率时,进行局部搜索,否则进行全局搜索,产生蚂蚁的新位置,同时采用边界吸收的方式,将蚂蚁位置界固定在取值范围内。

4) 计算蚂蚁新位置的适应度值,同时判断蚂蚁是否移动,并且计算新的信息素。

5) 若满足终止条件,则结束整个搜索过程,并输出优化结果,对应的参数为LEVY法参数的最优解;若不满足,则返回第2)步继续进行优化迭代。

ACO-LEVY辨识流程如图3所示。

图3 ACO-LEVY辨识流程框图Fig.3 ACO-LEVY identification flowchart

3 验证结果及分析

由于飞行数据采集时会受到外界环境干扰以及系统本身不利因素影响,使得数据产生系统误差和随机误差,因此需要对数据进行预处理。本文采用去趋势项以及野值的剔除和补正来消除传感器在获取数据时产生的偏移并提高数据的置信度,使用低通滤波和对数据平滑处理达到消减干扰信号的影响。

分别选取横、纵通道各1组扫频飞行数据作为辨识样本进行数据预处理、加窗及偏相干分析得到频率响应曲线。通过LEVY法计算初始模型结构后,在蚁群规模为50,迭代次数为100次的情况下,采用ACO优化LEVY模型参数。横向通道和纵向通道的适应度值变化如图4、图5所示,可以看出横向通道和纵向通道迭代次数在76和71时曲线趋于平稳,此时最小适应度值所对应的参数即为最优解,结果如表1所示。

图4 横向通道适应度进化曲线Fig.4 The fitness evolution curve of the lateral channel

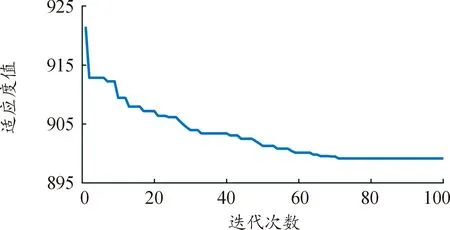
图5 纵向通道适应度进化曲线Fig.5 The fitness evolution curve of the longitudinal channel

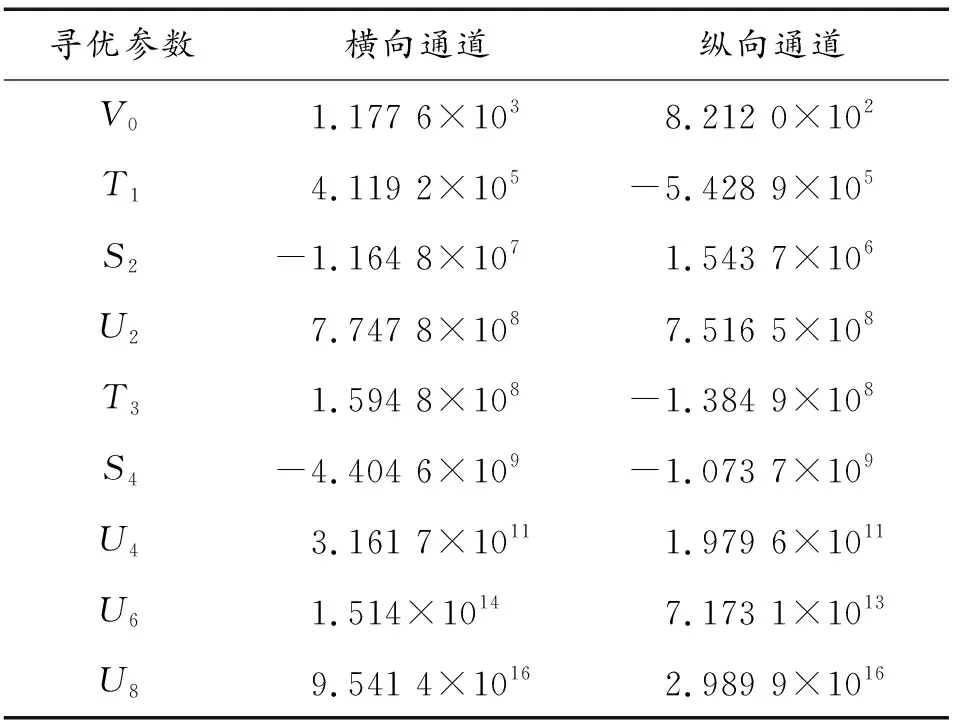
表1 参数优化结果Table 1 Parameter optimization results

将表1中参数代入式(33)中,得到横向通道传递函数模型为:

(35)

纵向通道传递函数模型为:

(36)

对小型无人直升机横向、纵向传递函数进行求解,其中,一组较为相近的特征根为小型无人直升机执行舵机的传递函数。对式(13)和式(14)中小型无人直升机结构参数取常数值,则辨识结果如表2所示。

表2 参数辨识结果Table 2 Parameter identification results

为验证模型的有效性,采用非辨识样本的扫频输入作为模型的激励信号,将得到的模型输出与真实飞行输出进行对比结果如图6、图7所示。图中:Ipwm为舵机的控制输入,p和q为滚转角和俯仰角速率,可以看出所辨识的模型能够较为精确地预测小型无人直升机飞行特性。

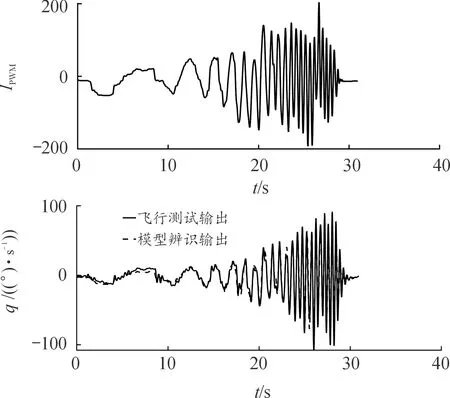
图7 纵向通道模型时域验证Fig.7 Time domain validation of longitudinal channel model

将所研究的算法与文献[7、12,18]中本领域广泛应用且效果较好的算法(后文简称“常规算法”)进行比较,该常规算法采用频域响应曲线幅值和相位最小化来确定传递函数,如式(37)所示。

(37)

式中:nω为频率采样点的数量;ω1和ωnω表示拟合的起始和终止频率;| |表示频率ω处的幅值;∠表示频率ω处的相位;Wγ表示频率ω处的相干值;Wg和WP为幅值和相位的权重,通常Wg取1,Wg取0.017 45。

选取横向、纵向通道小速度前飞数据片段作为模型的输入数据,得到的辨识输出结果与常规辨识方法输出结果进行对比。横向、纵向通道辨识结果如图8、图9所示。

图9 纵向通道小速度前飞时域验证Fig.9 Time domain validation for longitudinal channel during a low speed forward flight

辨识误差如图10所示。由图可知,ACO-LEVY方法辨识的模型能够较为准确预测飞行测试输出,且输出误差小于常规方法。

图10 小速度前飞辨识误差Fig.10 Error in identification for a low speed forward flight

为了全面评估ACO-LEVY方法的适应性和可信度,分别对横向、纵向通道取5组悬停及小速度前飞的飞行数据片段进行时域验证,以均方误差eMS、平均绝对误差eMA和决定系数R2作为评价指标,结果如表3、表4所示。决定系数R2的表达式为:

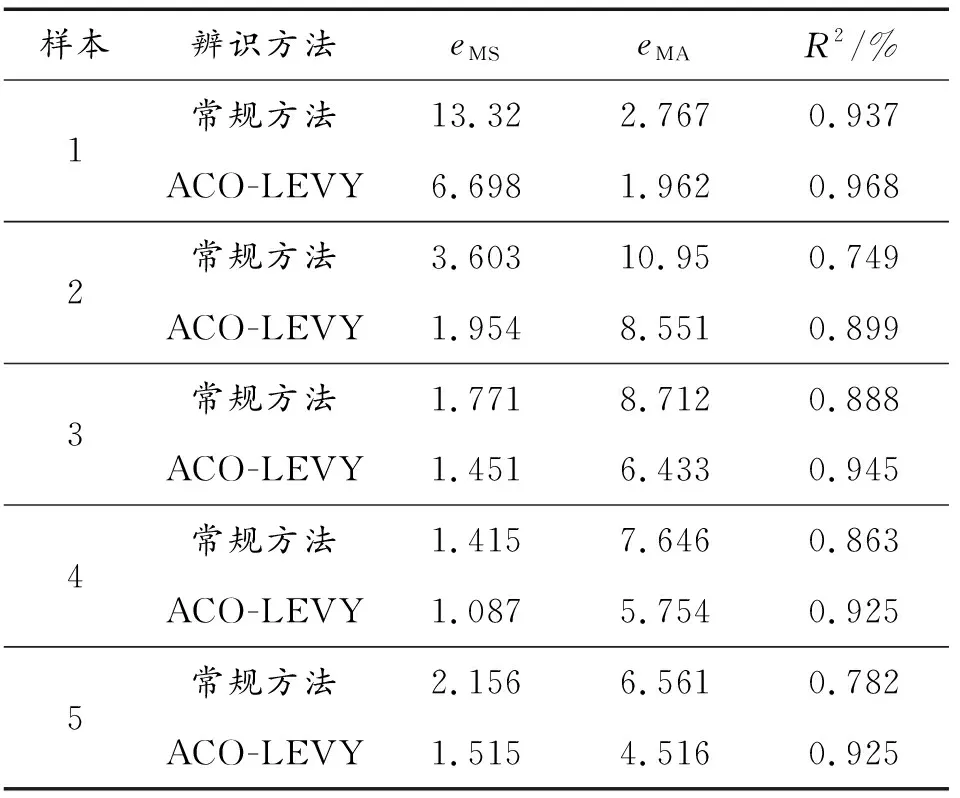
表3 横向通道预测精度分析Table 3 Analysis of prediction accuracy of lateral channel

表4 纵向通道预测精度分析Table 4 Analysis of prediction accuracy of longitudinal channel

(38)

从表3、表4可以看出:横向通道在5组不同的验证样本下,ACO-LEVY方法预测输出的MSE值比常规方法平均降低33%;MAE值比常规方法平均降低27%;R2值比常规方法平均提升10%。

纵向通道在5组不同的验证样本下,ACO-LEVY方法预测输出的MSE值比常规方法平均降低40%;MAE值比常规方法平均降低28%;R2值比常规方法平均提升12%。

由以上结论可知,采用ACO-LEVY方法所得到的传递函数模型能够更好地预测输入与输出间的关系。相比于常规方法,ACO-LEVY法的辨识模型结果在预测小型无人机的输出结果上具有更高的精度,更加真实地反映小型无人直升机的动态特性。

4 结论

本文针对频域辨识中曲线拟合的问题,提出了一种改进的频域辨识方法,通过飞行数据验证可以得到以下结论:

1) ACO-LEVY法拟合频域曲线所得到的动力学模型能够较好地反映小型无人直升机输出动态特性。

2) 所提出的方法得到的模型预测结果相比于常规方法,横向和纵向通道的均方误差降低了33%和40%,平均绝对误差降低27%和28%,决定系数提升10%和12%。

3) 针对不同的辨识对象,该方法具有通用性,只需改变目标的数学模型,便能得到对应的优化模型结果。