PBX-9404炸药临界起爆特性数值模拟

栗丁丁,何中其

(南京理工大学, 南京 210094)

0 引言

隔板实验是用于测定炸药冲击起爆特性的典型方法,利用临界隔板值定性表征不同试样的相对冲击波感度大小。冲击波感度是指在冲击波作用下,炸药发生爆轰的难易程度,是衡量炸药安全性能的一个重要指标[1],为了能够定量表征该临界条件,很多人用冲击波压力表征试样的冲击起爆阈值[2-4],因此我们用临界隔板厚度和临界起爆压力来描述试样炸药的临界起爆特性。

在隔板实验过程中,冲击波会经过有机玻璃进入试样炸药,探究冲击波在有机玻璃中的衰减规律,可以为试样炸药临界起爆特性的研究奠定基础,当然隔板材料的差异、试件壳体厚度的不同、点火方式的改变都会影响试样炸药的临界起爆特性,有学者在这些方面做过研究,例如文献[5]采用PVDF压电式压力传感器测量了在平面波透镜加载下经不同厚度有机玻璃隔板衰减后的冲击波压力历程,结果表明冲击波加载及装置尺寸的不同,密实介质的衰减系数会有所差别;文献[6]获得了由有机玻璃与LY-12铝合金组合的双层介质隔板排序、总厚度与厚度分配对透射到被发炸药中冲击波各参量的影响规律,认为选取波阻抗递增的排序时,透射冲击波能量较低,对炸药的安全性更有利。

模拟计算中,常常采用Lee-Tarver点火增长模型来描述试样炸药的冲击起爆过程[7],但是对于PBX-9404炸药,不同学者给出的Lee-Tarver参数存在一定的差异,这些模型参数是否适合来描述炸药冲击起爆过程还需与实验进行对比验证。

由于隔板实验的零部件都是一次性的,做一次实验需要更换一次实验部件,不能做重复的实验,因此做冲击波起爆隔板实验需要消耗大量的人力、物力、财力,这就使得采用实验方法获得的实验数据非常有限且非常来之不易。目前对于PBX-9404炸药的临界起爆特性的研究鲜有报道,在数值模拟方面的研究也少之又少,因此本文采用数值模拟和文献验证的方法,对PBX-9404炸药的临界起爆特性问题进行探究。

1 数值计算模型

1.1 几何模型

模型参考GJB772A—97中卡式隔板法的实验装置,按照实验尺寸建立计算模型如图1所示。图1中,主发药柱为钝化黑索今(RDX)药柱,药柱尺寸为直径40 mm、高度25 mm,密度为1 600 kg/m3;隔板材料为有机玻璃,隔板尺寸为直径40 mm;试件壳体和见证板材料为钢,尺寸分别为32 mm×26 mm×76 mm的钢管和100 mm×100 mm×6 mm的钢板;受发药柱选择PBX-9404炸药,密度为1 842 kg/m3。

图1 计算模型Fig.1 The calculation model

由于模型是轴对称模型,因此建立二维模型更方便计算。主发药柱RDX采用Euler算法,建立一个可以覆盖RDX爆炸范围的空气计算域,其余部分采用Lagrange算法。欧拉网格尺寸0.67 mm×0.67 mm,拉格朗日网格尺寸0.5 mm×0.5 mm。通过join设置连接,连接隔板、试件壳体与验证板,通过interaction设置接触,隔板与试样炸药、试样炸药与试件壳体和验证板的作用过程均采用Lagrange/Lagrange耦合算法计算。

1.2 材料模型

空气材料采用IDEAL AIR状态方程,其表达式为:

p=(γ-1)ρe-pshift

(1)

式中:P、γ、ρ、e和pshift分别为压力、绝热指数、密度、内能和初始压力。

试件壳体材料和见证板采用材料库里的Steel 4340,状态方程选用Linear,强度模型采用Johnson-cook,失效模型基于Mott破片分布理论的Stochastic随机破坏模型[8],失效准则为Principal Stress,Principal Tensile Failure Stress值取0.035 Mbar,侵蚀准则选用Geometric Strain,Erosion Strain值取1。强度模型表达式为:

(2)

主发药柱为RDX,状态方程选用JWL EOS;隔板材料为有机玻璃,状态方程采用shockEOS,具体模型参数见表1。

表1 RDX及有机玻璃的材料参数Table 1 Material parameters of RDX and Plexiglass

被发药柱试样PBX-9404炸药在描述冲击波起爆过程时采用Lee-Tarver三项式点火增长反应速率模型,即:

G1(1-λ)cλdpy+G2(1-λ)eλgpz

(3)

式中:λ、t、ρ分别为反应度、时间、密度;I、G1、G2、a、b、c、d、e、g、x、y和z这12个参数全部为常数。模型右边第1项表示炸药在冲击压缩作用下的热点点火阶段,当λ≥Fig max时该项为0;第2项表示热点缓慢燃烧阶段,当λ≥FG1 max时该项为0;第3项表示热点合并后炸药的快速反应阶段,当λ≤FG2 min时该项为0。该方程与JWL方程有很好的相容性,通常配套使用。

采用JWLEOS来描述PBX-9404炸药的未反应产物和爆轰产物的驱动膨胀过程,含温度形式的JWL状态方程形式为:

(4)

表2 PBX-9404炸药未反应炸药和爆轰产物JWL状态方程参数Table 2 Parameters of JWL equation of state for unreacted explosives and detonation products of PBX-9404 explosives

1.3 Lee-Tarver反应速率参数的确定

由于PBX-9404炸药在材料库里有多组Lee-Tarver反应速率方程参数,为了研究炸药Lee-Tarver模型参数对计算结果的影响,选取合适的模型参数来正确描述炸药冲击起爆过程,选取PBX-9404炸药的3组不同Lee-Tarver模型参数[10-12],建立与文献中实验模型一样的计算模型,分别计算这3种模型参数对应的临界起爆速度,并将计算结果与文献[13]中试验结果对比。表3给出了本文选取的3组PBX-9404炸药Lee-Tarver模型参数,表4为计算结果与试验结果的对比,所得计算结果与文献[14]稍有差别,可能是由于在设置材料的失效和侵蚀状态方程时所取的参数值不同。

表3 PBX-9404炸药的Lee-Tarver反应速率参数Table 3 Lee-Tarver reaction rate parameters of PBX-9404 explosive

从表4中可知:采用不同参数得到的计算结果相差较大,采用Bahl 1981反应速率参数计算得到的临界起爆速度最接近实验结果,相对误差大概为3.75%,这说明该组参数可以很好的描述冲击起爆炸药一系列问题;采用Tarver 1981反应速率参数的计算结果与实验结果相差较大,相对误差约为19.65%;采用Tarver 1985的反应速率参数计算时,PBX-9404炸药在很小的速度情况下依然能发生爆轰,所得计算值远远小于实验结果,表明Tarver 1985参数不适合描述PBX-9404炸药的冲击起爆过程。

表4 参数计算结果与实验结果对比Table 4 Parameter calculation results compared with experimental results

为了进一步验证参数选取的准确性,采用上文的计算模型,用本文选取的3种Lee-Tarver反应速率参数对卡式隔板试验进行数值模拟,计算结果如表5所示,在表5中,δr为临界隔板厚度,Pr为临界起爆压力。

表5 不同参数隔板试验计算结果Table 5 Calculation results of different parameters of diaphragm test

由上述对3种不同Lee-Tarver反应速率参数模拟计算的结果可知:本文选取的3种点火增长模型参数所得出的计算结果有一定的差异,尤其是选用Tarver 1985模型参数时,计算结果与其他2组参数相差太大。采用这3种参数来描述试样炸药冲击起爆过程的计算结果与上面计算临界速度阈值计算结果非常相似,从定性的角度谈,临界速度阈值和临界隔板厚度一定程度上都可以反映被发试样冲击起爆的感度大小,临界起爆速度越大,说明被发试样越不容易被冲击起爆,同样地,临界隔板值越小,则临界起爆压力越大,说明被发试样越不容易被冲击起爆。我们从定性的角度可以得出:按临界起爆速度来排序,Bahl 1981>Tarver 1981>Tarver 1985;按照临界起爆压力来排序,Bahl 1981>Tarver 1981>Tarver 1985,并且Tarver 1985模型参数在描述2类冲击起爆问题时表现出同样的问题,在上文中模拟得出的计算结果与文献实验进行对比后确定了Lee-Tarver状态方程参数,即采用Bahl 1981模型参数,这再一次印证了上文提到的选取模型参数的准确性。

因此,在数值模拟冲击起爆炸药时,模型参数的选取需谨慎。本文后续开展卡式隔板实验冲击起爆装药的数值模拟均采用Bahl 1981反应速率参数。

2 冲击波在有机玻璃中衰减规律的研究

在计算PBX-9404炸药冲击起爆特性前,首先利用数值模拟方法对冲击波在有机玻璃中的衰减规律进行研究,一方面能够验证数值模拟的准确性,另一方面还能够进一步研究冲击波在有机玻璃中传播的其他特性,为进一步研究PBX-9404炸药的冲击起爆特性奠定基础。

2.1 计算模型

冲击波在有机玻璃中的衰减规律计算模型参照上面卡式隔板法的实验模型建立,各个部分尺寸如图2所示,具体材料参数见表1,具体算法尺寸参见上文。在轴向处每隔5 mm设置一个检测点。

图2 有机玻璃衰减模拟模型图Fig.2 Plexiglass attenuation simulation model diagram

2.2 计算结果

通过数值模拟,我们可以清楚地观察到冲击波在有机玻璃中的动态传播过程:主发药柱RDX爆轰产生的冲击波在3.0 μs时到达有机玻璃上表面,此时显示的最大压力值为18.96 GPa,通过观察检测点9我们得出它的入射冲击波压力为16.78 GPa;在3.0 μs后冲击波开始在有机玻璃中传播,可能是由于点起爆的原因,冲击波前沿波阵面呈现一定的曲率向下传播,随着冲击波逐渐往下传播,冲击波压力值越来越小,有机玻璃的形变也越来明显;在12.0 μs时,爆轰冲击波到达有机玻璃下表面,可以判断出冲击波在有机玻璃中大概传播了9.0 μs。有机玻璃不同位置的压力分布图如图3所示。

将模拟得到的各个检测点的冲击波压力峰值列于表6。从表6可以看出,随着隔板厚度的增加,各个点的压力峰值越来越低,逐渐减小,而且减小的速度越来越慢,也即减小的幅值逐渐降低,与文献实验结果对比发现数值相差不大。其中δg为隔板厚度,Pm为模拟结果压力峰值,Ps为文献[15]实验结果压力峰值。

表6 冲击波压力峰值计算值与实验值比较Table 6 Comparison between calculated and experimental values of shock wave pressure peak

冲击波压力在密实介质中符合指数形的衰减规律为[16]:

P=ke-α.x

(5)

将式(5)两边取对数,可得:

lnp=lnk-α.x

(6)

即lnp与x呈线性关系,由表6中模拟数据拟合得出的lnp与x的关系曲线见图4,拟合曲线得到的关系式为:

图4 ln p与x的关系曲线Fig.4 The relationship between ln p and x

lnp=2.677-0.042x

将冲击波压力衰减情况的模拟结果与实验结果进行对比,结果如图5所示,可以看到这2条曲线吻合得较好。由图5可知,数值模拟的初始压力较文献结果低约1 GPa,这可能是因为主发药柱RDX的冲击阻抗值ρD大于有机玻璃的冲击阻抗值ρmDm,产物中反射波为稀疏波,界面上的压力Px将比爆炸产生的爆轰波的C-J压力PJ低,也即数值模拟的初始压力计算结果较文献实验结果低。

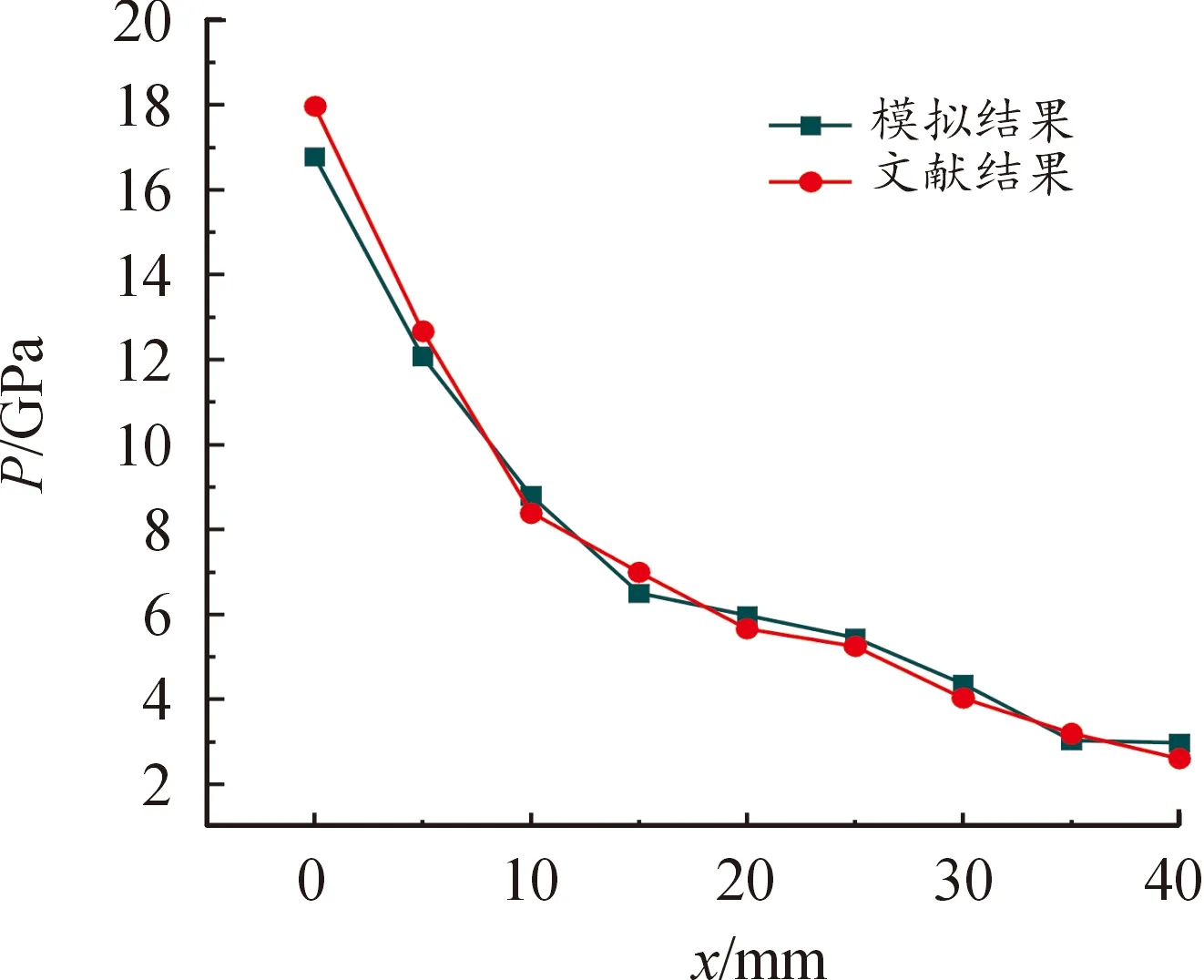
图5 冲击波压力衰减情况的模拟结果与实验结果对比Fig.5 Comparison of simulated and experimental results of shock wave pressure attenuation

采用式(5)、式(6)处理表中数据,可以得到不同位置压力P与隔板厚度x的衰减规律关系式:P=14.55e-0.042.x。上式表明冲击波压力在有机玻璃直径为40 mm的情况下的衰减系数值为0.042,与文献中的0.05相差较小,说明模拟结果与实验结果有较好的一致性,进一步验证了数值模拟的准确性。

3 数值模拟结果及分析

由以上的数值模拟跟实验的比较结果不难看出,数值模拟的准确性,数据与实验结果基本吻合,也即采用该Lee-Tarver状态方程参数能够较好地描述PBX-9404炸药冲击起爆过程。接下来,通过改变一种条件、其他条件不变的控制变量法,研究PBX-9404炸药的冲击起爆特性,通过改变隔板材料、壳体厚度、点火方式3种方式来观察对PBX-9404炸药临界起爆特性的影响规律。

在隔板实验过程中主要是通过观察底部见证板的凹痕程度来判断试样炸药爆轰与否,而在数值模拟中主要通过观察各个监测点的压力时程曲线的峰值压力的变化趋势和反应度曲线的变化趋势。若压力峰值逐渐上升且达到试样的爆轰压力说明试样发生爆轰,峰值压力逐渐下降说明没有发生爆轰;若反应度曲线斜率越来越大且最终达到1,则认为试样发生爆轰,否则没有发生爆轰。典型压力波形图如图6所示,图6(a)为没有发生爆轰,图6(b)为发生爆轰;典型反应度曲线波形图如图7所示,图7(a)反应度曲线斜率越来越小且没有达到1即未发生爆轰,图7(b)为发生爆轰。

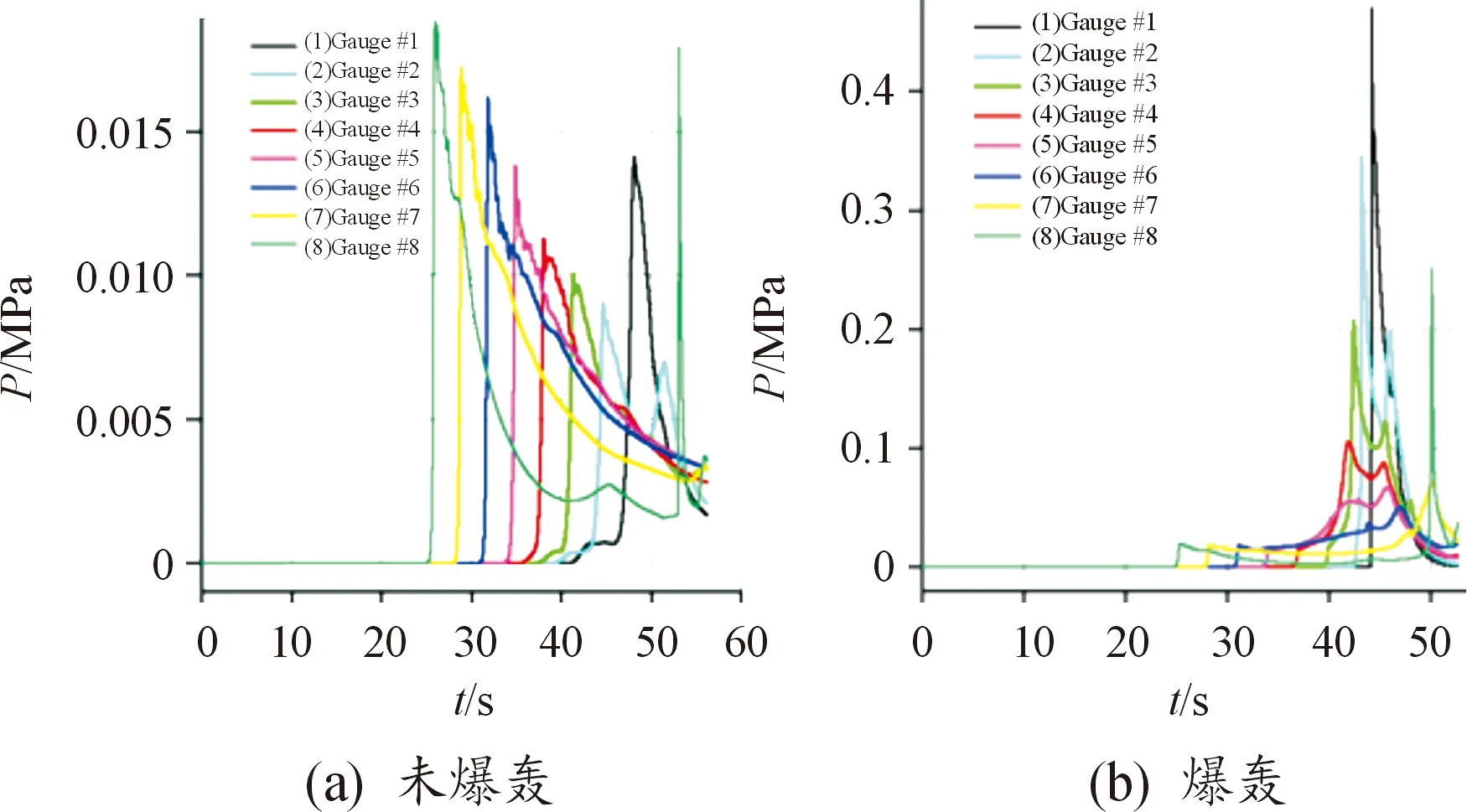
图6 压力时程曲线波形Fig.6 Pressure time history curve waveform

图7 反应度曲线波形Fig.7 Responsiveness curve waveform

3.1 隔板材料对临界起爆特性的影响

除了上文提到的有机玻璃外,还选择了阻抗强度相差较大的铝(AL6061-T6)和钢(STEEL4340)作为隔板材料,分别进行数值模拟,来研究隔板材料对临界起爆特性的影响。在模拟中采用隔板厚度步长为1 mm,根据上文提到的冲击起爆的压力峰值和反应度曲线作为判断准则,来判断试样是否发生爆轰,表7为数值模拟得到的计算结果,其中ρD代表隔板材料的冲击阻抗值[17]。

表7 临界起爆特性数值模拟的计算结果Table 7 Calculation results of numerical simulation of critical detonation characteristics

从表7可以看出,临界隔板厚度小的冲击阻抗大,临界隔板厚度大的冲击阻抗小。钢的临界隔板厚度最小,冲击阻抗最大,有机玻璃的临界隔板厚度最大,冲击阻抗最小,两者的隔板值相差较大,这是由于冲击波在钢板中的衰减程度最高,在机玻璃中的冲击波衰减程度相对低。还可以看出,虽然隔板材料不同,但由于试样炸药和试件壳体材料都不变,PBX-9404炸药的临界起爆压力差别不是很大。

3.2 壳体厚度对临界起爆特性的影响

为了得到不同试件壳体厚度对PBX-9404炸药临界起爆特性的作用规律,在其他条件不变的情况下,隔板材料依然选择有机玻璃,我们分别选取17 mm筒壁厚度的钢管作为试件壳体,厚度步长为1 mm,壳体厚度对临界隔板厚度和临界起爆压力的关系如图8所示。图8中黑色方形曲线反映壳体厚度与临界隔板厚度的关系,红色圆点形曲线反映壳体厚度与临界起爆压力的关系,为壳体厚度。

从图8中可以看出,当壳体厚度为1 mm时,促使炸药发生爆轰的临界隔板厚度为79～80 mm,对应的临界起爆压力为2.303 9～2.357 0 GPa,隔板厚度大于此值或起爆压力小于此值,试样炸药都不会发生爆轰,当壳体厚度为2 mm时,临界隔板厚度为82～83 mm,对应的临界起爆压力为2.174 1～2.213 0 GPa,同样地,当壳体厚度为3 mm时,临界隔板厚度为83～84 mm,对应的临界起爆压力为2.113 4～2.174 1 GPa。从图8中正方形点曲线可知:PBX-9404炸药的临界隔板厚度随着试件壳体厚度的增加逐渐增加,但当壳体厚度增加到5 mm时,临界隔板厚度增长到86～87 mm,此后不再发生改变;从圆点形曲线可知:临界起爆压力随壳体厚度的曲线变化正好与临界隔板值随壳体厚度的曲线变化相反,这说明增加试件壳体厚度可以更容易的使试样炸药发生爆轰,同样的,当试件壳体厚度增加到5 mm时,临界起爆压力为1.999 4～2.036 7 GPa,此后在随着壳体厚度的增加,起爆压力的临界值虽然稍有浮动,但大致趋于2.03 GPa。

图8 壳体厚度对临界隔板厚度和临界起爆压力的影响Fig.8 Influence of shell thickness on critical diaphragm thickness and critical initiation pressure

产生这种现象的原因与试件壳体侧向的稀疏波有关。 C.M.Tarver、P.A.Urtiew和K.Bahl等[18-19]对LX-04、LX-17药柱在没约束和弱约束下的冲击感度进行了研究,认为弱约束下的冲击感度较没约束时有所增加,并作出了相应的解释。增加壳体厚度,爆轰波延径向传播的难度增大,阻碍了试样爆轰产物径向做功的能力,减小了径向能量损失,使得试样炸药爆轰产物有更多的能量来推动爆轰波的传递,从而使得试样更加容易发生爆轰,也即增加试件壳体厚度可以使试样爆轰更加容易。

3.3 起爆方式对临界起爆特性的影响

除了隔板材料、壳体厚度的差异会对PBX-9404炸药的临界起爆特性有所影响,点火方式的不同也是一个重要的影响因素。在AUTODYN软件中通过Detonation选项分别设置点起爆、环起爆、面起爆,图9为不同起爆方式下起爆点示意图,内部区域为RDX药柱,外部为整个空气计算域,红色部分为起爆点。

图9 不同起爆方式起爆点示意图Fig.9 Schematic diagram of the detonation point of different detonation methods

在数值模拟软件中分别采用中心点、环和面起爆3种方式对RDX进行点火,数值模拟结果如表8所示。

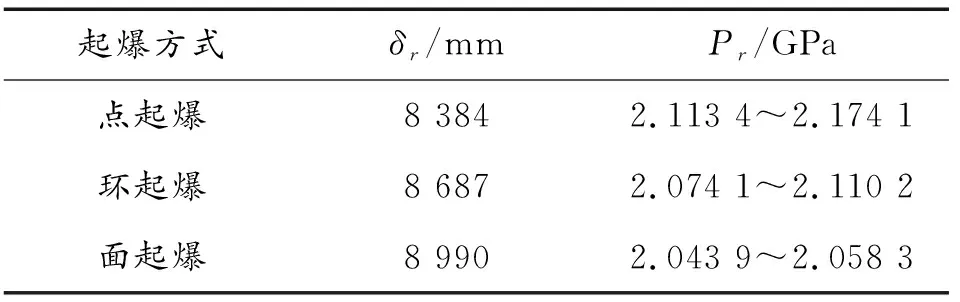
表8 起爆方式对临界起爆特性的影响Table 8 Influence of detonation mode on critical detonation characteristics

由表8可知,采用点起爆时,临界隔板值最小,采用面起爆时,临界隔板值最大。在这3种起爆方式中,面起爆的临界起爆压力略小,但都趋于2.1 GPa左右。可以推断出,改变起爆方式可以使反应更加完全,从而爆轰产物产生的压力值能更好地通过有机玻璃隔板,即面起爆下反应更加完全,采用该方式下的临界隔板厚度最大。

4 结论

本文采用数值模拟与文献验证的方法,应用AUTODYN软件与点火增长模型模拟计算PBX-9404炸药的临界起爆特性,主要得出以下结论:

1) 在本文选取的3种Lee-Tarver模型参数中,Bahl 1981的反应速率参数可以更好地描述PBX-9404炸药的冲击起爆过程,使用该模型参数下的临界隔板厚度为83～84 mm,临界起爆压力为2.113 4～2.174 1 GPa;

2) 冲击波在有机玻璃中传播规律的数值模拟中发现,不同位置压力P与隔板厚度x的衰减规律关系式为P=14.55e-0.042.x,衰减系数值为0.042,与文献中的0.05比较近接,再一次验证了数值模拟的可靠性;

3) 通过改变隔板材料,得出钢的临界隔板厚度最小,冲击阻抗最大,有机玻璃的临界隔板厚度最大,冲击阻抗最小,但临界起爆压力相差不大;通过改变试件壳体厚度,随着试件壳体厚度的增加,炸药的临界隔板厚度逐渐增加,临界起爆压力逐渐减小,当壳体厚度增加到5 mm时,此后在随着壳体厚度的增加,两者不再发生变化;通过改变起爆方式,面起爆时临界隔板值最大,点起爆最小。