基于PSO-SES-BPNN算法的液压系统故障诊断模型

战 欣,刘卓娅

(珠海科技学院, 广东 珠海 519041)

0 引言

一直以来液压系统的故障诊断问题都是工程技术人员的重点研究对象。液压系统包含许多回路,系统由许多元件组成,元件之间存在时空耦合关系。因此,液压系统在运行过程中发生故障的概率较高,故障模式具有隐蔽性、随机性和复合性等特点[1]。例如组件之间的泄漏,摩擦变化,流体特性变化,传感器问题和供应压力变化,这些都会导致系统性能下降。如果未及时检测到这些故障,将导致完全的系统故障[2]。这将造成人员生命和财产损失。

于喜金等利用BPNN对VMD方法处理后的液压管路信号进行故障诊断,诊断准确率达99.32%[3]。Zhao等[4]采用反向传播神经网络算法对液压系统进行故障诊断。Helwig等[5]运用人工神经网络和支持向量机算法解决液压系统故障诊断问题,最好故障诊断准确率平均值为82.6%。Peng等[6]利用DBA最近质心和随机森林时间序列方法对与本文中液压系统相同的数据集进行故障诊断,故障诊断准确率最高为95.11%。

综合对比上述故障诊断算法,本研究中建立了基于PSO-SES-BPNN的故障诊断优化算法,考虑MBGD对BPNN算法性能影响机理,采用SES对MBGD进行改进;由于各种神经网络算法的超参数问题一直是困扰研究人员的难题[7],本文中利用PSO对SES-BPNN算法的主要超参数进行了优化,同时以故障诊断准确率为评价指标寻找最优超参数取值组,最终确定了最优液压系统故障诊断模型。

1 液压系统的数据特征

1.1 液压系统结构

液压系统实验平台数据来源于UCI上的公共数据集。液压系统由2部分组成。

图1(a)为主工作回路,图1(b)为辅助冷却-过滤回路。这2个部分通过油箱连接,系统有14个用于测量过程值的传感器:压力传感器PS1～PS6,流量传感器FS1和FS2,电机功率传感器EPS1,振动传感器VS1,温度传感器TS1～TS4。

图1 液压系统原理图Fig.1 Schematic diagram of hydraulic system

1.2 数据处理

本研究处理了14个传感器数据和3个人工参数数据:Efficiency factor、Virtual cooling efficiency、Virtual cooling power,并将上述17个参数直接作为特征。

1) 同频处理

这17个参数的采样频率有3种,分别是100、10、1 Hz,具体取决于基础物理值的动态。为了方便数据分析,将17个参数都转换成采样频率为10 Hz的数据集。转换方法为:100 Hz转换成10 Hz:从采样周期的第一个数据开始,每10个数据求平均值构成新数据集;1 Hz转换成10 Hz:以TS1为例,TS1t为原数据集数据值,TS1ti为转换后新数据集数据值。

TS1t0=TS1t

(1)

(2)

2) 归一化处理

由于传感器类型和物理量不同,样品的大小处于不同的水平。众所周知,比较不同量级的数据是毫无意义的。该液压系统17个参数的类型和物理量不同,因此样本的大小处于不同的级别。因此,对17个参数做数值归一化处理。归一化区间为[0,1],归一化为

(3)

式中:x为原始数据;xmax为原始数据的最大值;xmin为原始数据的最小值;x′为原始数据的归一化生成值。

1.3 故障数据集

液压系统的结构非常复杂,并具有多种类型的故障[5]。故障说明见表1所示。

表1中的液压系统有4种可能发生故障的元件,每种元件又有不同程度的故障状态,例如:泵有弱泄漏和严重泄漏2种故障状态。液压系统也可能处于同时几个不同元件出现了不同程度的故障状态。为了验证各种液压系统故障诊断模型在不同复杂程度故障问题时的故障诊断性能,将数据集整理成单故障元件、双故障元件、3个故障元件、4个故障元件等4大类15个数据集。其中故障类型最简单的数据集中只有2种故障和无故障共3种状态,为三分类问题;其中故障类型最复杂的数据集共有各种故障和无故障状态共144种。

表1 液压系统的故障元件、模拟故障条件和故障级别Table 1 Fault component,simulated fault condition and fault level of hydraulic system

2 算法优化

2.1 BPNN算法

BPNN算法信息处理分为前向传播和误差的反向传播2个过程[8],如图2所示。BPNN算法的分类准确率取决于误差反向传播过程中,算法对权值和阈值的修正[9]。正是通过这个反向传播修正过程,使BPNN算法的分类结果与真值更接近[10]。

图2 BPNN算法原理图Fig.2 Schematic diagram of BPNN algorithm

BPNN算法反向传播的常用算法是梯度下降法,感知机权重的改进公式如式(4)所示,但该算法经常遇到鞍点问题,这将会导致BPNN算法陷入局部最优,而无法跳出[11]。随机梯度下降法和Mini批量梯度下降法遇到鞍点时大多数情况都可以使BPNN算法跳出鞍点,但这2种方法又都会带来新问题:每次梯度的方向不确定,可能需要很长时间才接近最小值点,而且不会收敛。在梯度的方向不确定问题上,MBGD法表现更好些。

(4)

BPNN算法与其他众多深度学习算法一样都有较多超参数,例如隐藏层有几层?每个隐藏层有多少个感知机?每个感知机的权重和阀值是多少?学习率是多少?选择哪种激活函数等。这些超参数的取值都对BPNN算法的分类准确性起着关键性的作用[12-13]。其中,感知机的权重和阀值可以由反向传播的算法解决。

2.2 一次指数平滑法

SES的原理是将本期观察值和本期预测值赋予不同的权重,并求和得到下一期预测值的方法,预测公式如式(5)所示。SES一般用在时间序列的预测问题,该方法将被预测变量在时间轴上前后值之间的影响关系引入预测公式。该算法的特点是被预测变量在时间轴上的每一点的值对后面的所有点的值都有影响,由于平滑系数的迭代关系,时间轴上距离越远的点彼此影响越小。

Ft+1=βYt+(1-β)Ft

(5)

式中:Ft+1为t+1期的指数平滑趋势预测值;Ft为t期的指数平滑趋势预测值;Yt为t期实际观察值;β为平滑系数。

2.3 SES改进的BPNN算法

(6)

(7)

(8)

1) 梯度下降法的鞍点问题主要是局部最优后面多点梯度g都为零,导致BPNN算法无法跳出局部最优,把局部最优误判断为全局最优。SES改进的MBGD算法计算的梯度不可能连续为零,因为引入的历史梯度值是在变的。

2) 随机梯度下降法一轮迭代只用一条随机选取的数据,因此,每次更新可能并不会按照正确的方向进行,参数更新具有高方差,从而导致损失函数会发生剧烈波动。MBGD算法为解决该问题,增加了一轮迭代随机选取的数据的数量,问题有所改善,但每次梯度的方向不确定性依然存在,可能需要很长时间才能接近全局最优值。BPNN是连续迭代优化的,所以每次反向传播对每个感知机的权重和阀值进行修正对下一轮的反向传播一定是有影响的,SES通过引入梯度g的所有历史值,平滑了每轮反向传播梯度g的波动。

2.4 PSO算法

PSO算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法[14]。将优化问题的搜索空间类比于鸟类的飞行空间,将每只鸟抽象为一个无质量、无体积的粒子,用以表征问题的可行解,优化问题所要搜索到的最优解则等同于鸟类寻找的食物源。文献[15-16]中分别利用PSO优化SVM、ANN和AdaBoost算法的超参数,算法的决策质量都有一定程度的提升。

在本文中涉及的优化问题中,若SES-BPNN算法多个需要优化的超参数的一组取值为一个粒子,优化过程所要搜索到的最优解则是SES-BPNN算法模型对液压系统故障诊断的最高准确率。

2.5 PSO优化的SES-BPNN算法流程

为获取液压系统故障诊断问题中的最佳取值,本文中利用PSO求取SES-BPNN算法的超参数,优化后的超参数即为所求最佳值。PSO对SES-BPNN算法超参数的优化流程如图3所示。其中,gbest_parameter为全局最优粒子的参数值,pbest_parameters为局部最优粒子的参数值,best_ fitness为全局最优适应度函数值,fitness_value为每个粒子的最优适应度函数值,particle swarm为当前全部粒子的所有参数值。

图3 PSO-SES-BPNN算法流程图Fig.3 Flow chart of PSO-SES-BPNN algorithm

根据粒子群算法机理,SES-BPNN算法需要优化的超参数的一组取值为一个粒子,优化过程所要搜索到的最优解则是液压系统故障诊断准确率的最高值。为了确保粒子在值域空间分布的广度,粒子群取值30个粒子,初始化时30个粒子对应的超参数均为随机取值。粒子的每轮优化都会根据全局最优和局部最优调整运动方向和运动距离。PSO共进行20轮粒子优化,全局最优粒子会被保存下来。

3 实验结果与分析

3.1 实验过程

1) 确定超参数优化对象

综合考虑SES-BPNN算法的各超参数对算法性能影响的程度,确定超参数优化对象,见表2所示。

表2 PSO-SES-BPNN算法的超参数取值范围Table 2 Value range of hyperparameters of PSO-SES-BPNN algorithm

2) 不同模型诊断过程

考虑采用相同算法解决不同的分类问题时最优模型的差别性,其本质是模型之间的参数不同,比如BPNN算法模型的隐藏层数量不同、各个隐藏层的感知机数量不同、学习率不同、激活函数不同等。一般情况下研究人员训练算法模型初始阶段要么随机赋值,要么使用Python语言自带库的参数默认值。因此,本文中所建立的液压系统故障诊断模型的超参数选取了Python语言自带sklearn库中MLPClassifier的参数默认值。PSO优化的SES-BPNN算法除了表2中需要优化的超参数,也选取了MLPClassifier的参数默认值。诊断过程如图4所示。

图4 诊断过程框图Fig.4 Flow chart of analysis

3.2 实验结果

为证明优化模型的有效性,本文中采用了与文献[4-6]中的数据,利用BPNN、SES-BPNN和PSO-SES-BPNN等3种算法对15种不同故障复杂度数据集进行训练和测试。对比3种算法模型的故障诊断性能,并将最优模型的故障诊断准确率与同数据源的文献研究成果进行比较。BPNN、SES-BPNN和PSO-SES-BPNN等3种算法的实验结果如表3和表4所示。

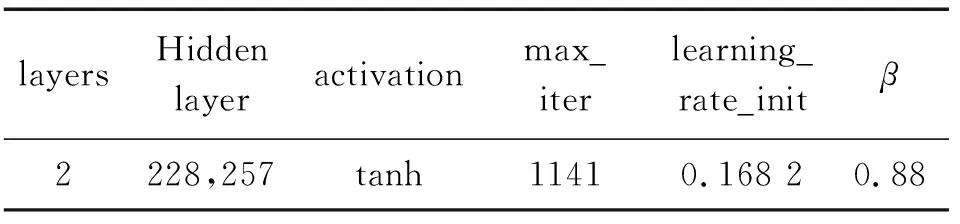
表3 最优故障诊断模型参数值Table 3 Parameter values of optimal fault diagnosis model

表4 3种算法测试结果统计Table 4 Statistics of test results of three algorithms

续表(表4)

表3为针对144种故障状态的数据集训练得到的PSO-SES-BPNN算法的最优故障诊断模型参数。

表4为BPNN、SES-BPNN和PSO-SES-BPNN等3种算法对15种不同故障复杂度数据集的训练模型的统计结果,其对比结果如图5所示。

图5 3种算法测试结果对比图Fig.5 Comparison diagram of test results of three algorithms

3.3 结果分析

由上述3种算法的实验结果可以看出,在相同的超参数,相同的数据集,相同的迭代次数,SES-BPNN算法模型对不同复杂度的15个故障数据集的诊断准确率都高于BPNN算法模型,表明了在不同复杂度的故障诊断问题中SES-BPNN算法都先于BPNN算法找到更优秀的模型。而且,2种算法的差别只在SES对BPNN算法反向传播中MBGD算法的改进。因此,可判断SES对MBGD算法的每次梯度的方向不确定问题的改善是有效的,算法的收敛性更好。根据表4的实验结果,PSO-SES-BPNN算法模型的故障诊断准确率远高于未优化超参数的SES-BPNN算法模型,可以得知,在15种不同故障复杂度数据集的故障诊断训练过程中PSO都为SES-BPNN算法找到了较优的超参数取值,确定了较适合的故障诊断模型。

同时表4中的实验结果表明,针对17个特征变量,相同的算法模型在诊断不同的液压元件故障问题时性能表现差别较大。如SES-BPNN算法诊断冷却器故障问题的准确率是0.793 2,诊断泵故障问题的准确率是0.739 4,说明冷却器不同程度的故障在17个特征变量上产生的数值变化较显著,更容易被模型诊断出来。因此,在引入PSO优化SES-BPNN算法时,冷却器故障诊断问题找到了非常好的故障诊断模型,其故障诊断准确率高达0.998 7。但有时又不完全符合上面的规律,如BPNN算法模型和SES-BPNN算法模型表现较差的泵故障诊断问题,在引入PSO优化SES-BPNN算法时,反倒找到了比蓄能器故障诊断模型更优的模型。上述2种现象说明,判断不同元件不同程度的故障在17个特征变量上产生的数值变化是否显著,还要以BPNN算法模型和SES-BPNN算法模型的诊断结果为准。其根本原因在于上述2个模型的训练过程没有引入随机因子,而PSO-SES-BPNN算法模型训练过程则不同,优化超参数的初始值就完全是随机的,如果第一步就找到了较优的超参数,那么之后训练出更加优质的故障诊断模型的概率必然会大大提高。

3.4 与同数据源文献对比

由于本文中采用了与文献[4-6]中相同的实验数据,结果对比见表5—表7。

表5 与文献[4]中的结果对比Table 5 Comparison with the results in the literature [4]

表6 与文献[5]中的结果对比Table 6 Comparison with the results in the literature [5]

表7 与文献[6]中的结果对比Table 7 Comparison with the results in the literature [6]

由对比结果可知,本文中建立的模型诊断准确率比文献[4]中的BPNN算法高24.5%,较文献[5]中的ANN算法平均高15%,远高于文献[6]中的NC-DBA算法诊断准确率,表明模型性能优势显著,更加有利于提高故障诊断效率。

4 结论

针对液压系统复杂多变的故障问题,本研究以反向传播神经网络算法为基础,以优化模型超参数为手段,建立了提高液压系统的故障诊断准确率的有效模型,结论如下:

1) SES对MBGD算法的鞍点和每次梯度的方向不确定问题的改善是有效的,算法的收敛性更好。

2) PSO可以为SES-BPNN算法找到优质的超参数取值,与同类型研究相比,优化后的SES-BPNN算法的故障诊断模型对各种不同复杂度的故障数据集的平均故障诊断准确率可达98%,诊断性能大幅提升。