基于多场耦合仿真的四轨电磁发射器性能分析
杜翔宇,刘少伟,关 娇
(1.空军工程大学 防空反导学院, 西安 710051;2.空军工程大学 信息与导航学院, 西安 710051)
0 引言
电磁轨道发射器是一种借助电磁力做功的新概念发射方式,具有动能大、初速高等优点,被认为是未来军事领域发射技术发展的方向。但在电磁轨道发射器走向工程化的过程中,仍然面临许多问题,其中最重要的2个问题分别是高速滑动条件下的接触失效问题和复杂的多物理场现象相互耦合问题。针对这2个问题,国内外许多学者进行了针对性研究。
对于接触问题,朱仁贵等[1]研究了过盈配合对枢轨初始接触特性的影响;冯登等[2]研究了接触压力的分布特性;朱春燕等[3]通过实验分析了发射过程中接触电阻的变化;Hsieh等[4]研究了接触电阻与接触压力的关系。这些研究结果表明,为了保证电枢在高速状态下稳定运行,必须采用枢轨无间隙过盈配合方式,这就导致电磁轨道发射器工作过程中恶劣的接触状态难以避免,只能通过合理的结构设计改善。对于发射器多物理场耦合问题,Lin Qinghua等[5]开发了场路耦合条件下电磁轨道发射器的多物理场求解器;Yin等[6]对简单C形电枢的膛内电磁特性进行了研究;Galanin等[7]基于准静态磁场对电磁轨道发射器的工作过程进行了仿真;Kim等[8]研究了发射器的电流分布与电感梯度;Li Baoming[9]对增强型电磁发射器的电-热耦合特性进行了分析,还对发射器的大变形现象和损伤特性进行了研究[10]。上述研究结果表明,电磁轨道发射器的多物理场耦合现象极大影响发射器性能,采用合适的电磁轨道发射器结构确实能够达到改善接触特性的目的。
本文设计了一种四极凸轨道电磁发射器结构,并基于电磁-热-结构耦合有限元-边界元仿真模型对其动态发射过程进行了研究,分析了电枢运动过程中的瞬态受力情况和接触特性、电磁特性、温度特性。
1 控制方程与模型参数
本文中以螺栓预紧型四极凸轨道电磁发射器作为研究对象,图1(a)所示为电磁发射试验平台,图1(b)所示为发射装置本体。由于发射装置中无铁磁性材料,且支撑体、紧固件等部件均与发射器电枢和轨道保持绝缘,研究表明对发射器的多物理场耦合特性影响较小,因此本文在研究发射器多物理场耦合特性时,不对这些部件进行建模。图1(c)所示为研究中采用的枢轨系统模型。
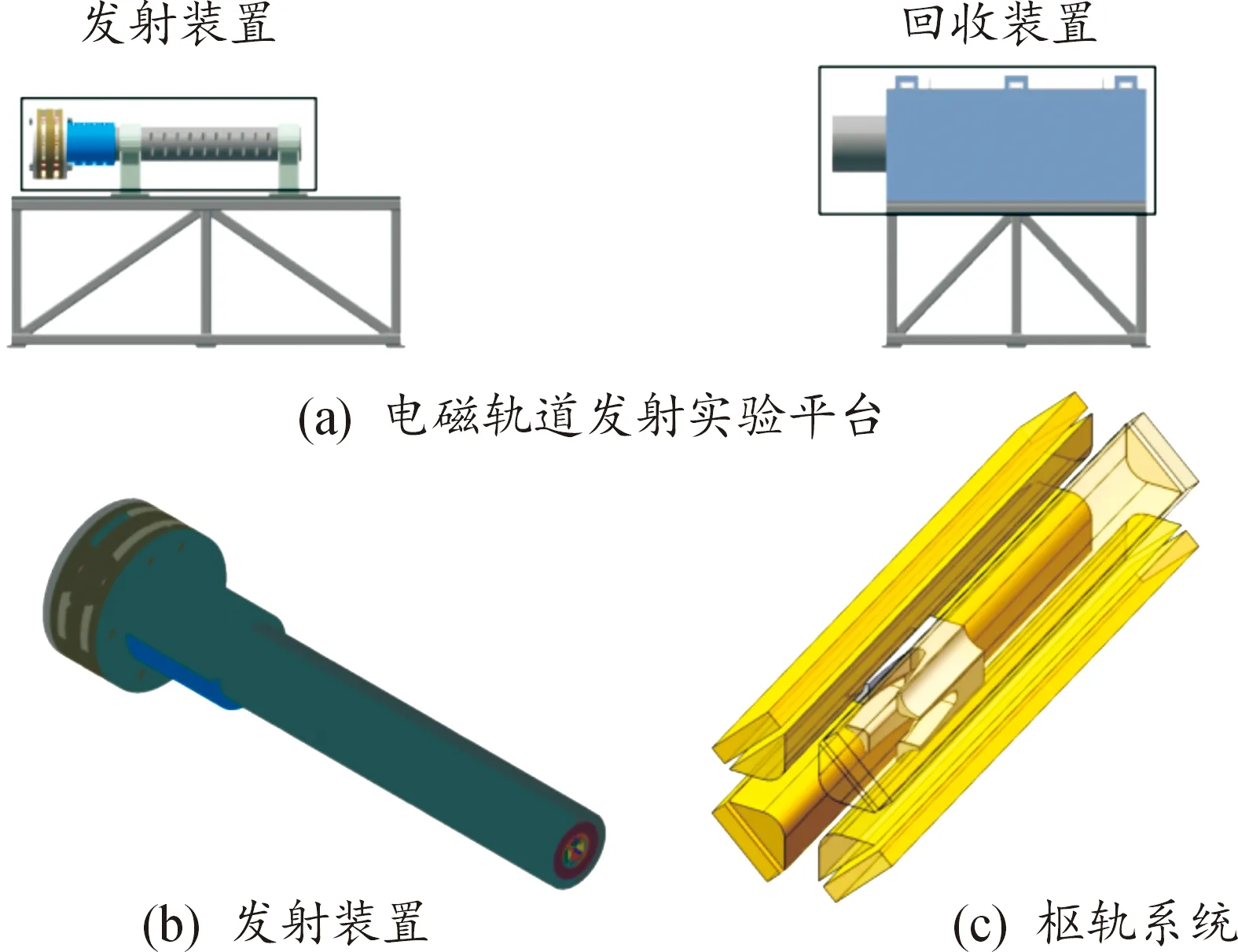
图1 发射试验平台结构Fig.1 Structure of the launcher test platform
模型中电枢与轨道的材料分别为6061铝合金和铬锆铜,模型具体参数见表1所示。
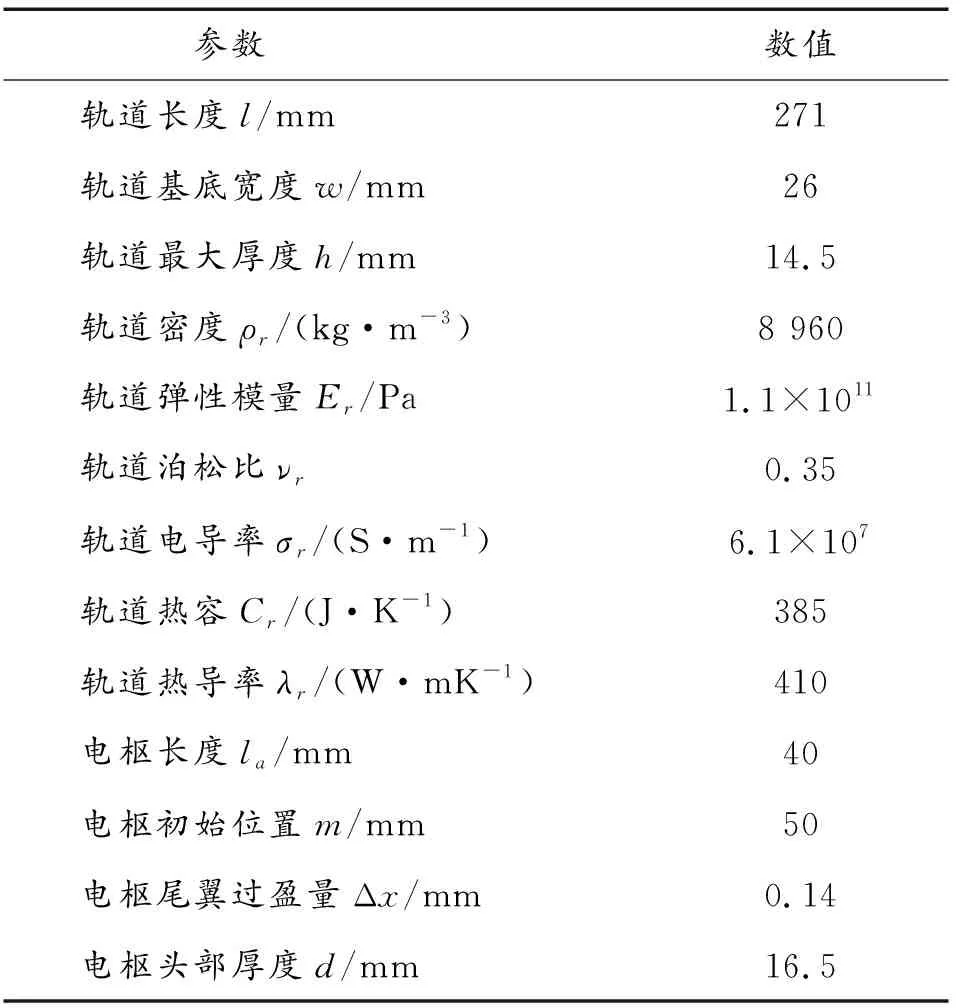
表1 模型参数Table 1 Paramaters of the model

续表(表1)
电磁轨道发射器的工作过程涉及电磁场、温度场、结构场等复杂的多物理场耦合现象,伴随着电磁相互作用下的电磁感应与趋肤效应,电枢与轨道之间的电流传导,电枢运动过程中的摩擦热、焦耳热生成与传递,电枢与轨道受力状态下的接触与变形等。发射器工作过程中涉及的多物理场耦合关系如图2所示。
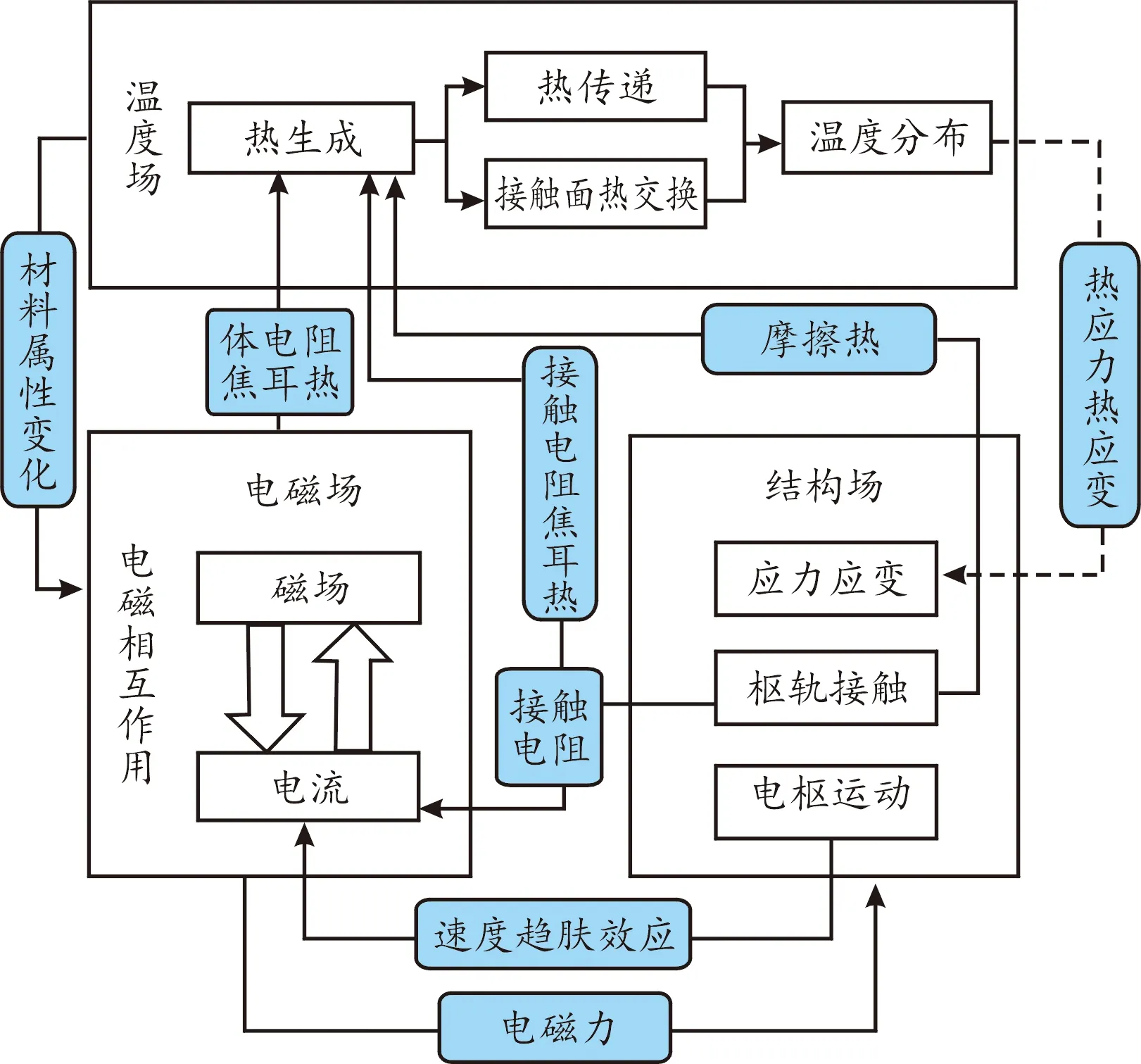
图2 电磁轨道发射器中的多物理场耦合关系Fig.2 Coupling relation of multiple physical fields in railgun
对于电磁场来说,由于脉冲电流频率较低,场强的变化与场源的变化之间几乎是无时延的,因此可以忽略传导电流,也就是说不考虑电场变化产生的磁场。基于该假设,采用磁矢势和电标势作为变量,可以将麦克斯韦方程组改写为:
(1)
(2)
式(1)称为磁场扩散方程,式(2)称为电流连续性方程。其中:A为磁矢势;φ为电标势;μ、σ分别为材料的磁导率和电导率;JS为源电流密度;v为导体运动速度。由于速度项v的存在,方程的数值计算稳定性较差。因此采用拉格朗日坐标描述运动导体,在拉格朗日坐标下,速度项v将消失。进而,关系电磁轨道发射器性能的几个关键物理量即可求得:
(3)
(4)
对于电磁轨道发射器的一般工作环境,可以近似认为空气域不导电。因此空气区域的电磁场控制方程退化为拉普拉斯方程:
▽2A=0
(5)
对于温度场,考虑热传导与热对流,其控制方程为:
(6)
q=h(T-Ta)
(7)
对于电磁轨道发射器而言,热源主要有焦耳热和摩擦热两项,其中摩擦热是作用在枢轨接触面上的边界热源,需要考虑滑动接触表面上的热流分配问题。考虑到电枢与轨道接触时间较短,假定热流分配系数为一常量。定义轨道获得的接触面热量的比例为:
(8)
式中:λ为导热系数;ρ为密度;c为比热容;下标a和r分别对应电枢和轨道。假定接触面上产生的热量全部传输给电枢和轨道而不发生耗散,那么二者从接触面热生成过程中可获得的热量分别为:
dQDr=DrdQc=Drd(Qcr+Qf)
(9)
dQDa=DadQc=(1-Dr)d(Qcr+Qf)
(10)
电磁轨道发射器特有的高速滑动电接触现象耦合了电磁场、结构场,严重影响发射器的性能,本文采用CLM模型计算接触电阻,实现电磁场与结构场的耦合CLM模型将不光滑的A-SPOT接触近似为连续的接触面,根据材料属性和接触压力按式(11)计算接触层的电阻。
(11)
式中:ρc为接触电阻率;lc为名义接触层的厚度;ρa为2种接触材料电阻率的算术平均值;Hsoft为2种接触材料中较软材料的硬度;P为接触压力。
由于电磁轨道发射器的材料均非铁磁性材料(磁导率较高),因此采用洛伦兹力公式即可准确计算发射器在工作过程中的受力:
(12)
基于发射器的受力,可以求得发射器各材料的变形情况,进而采用增广拉格朗日法计算接触压力。
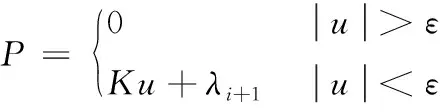
(13)
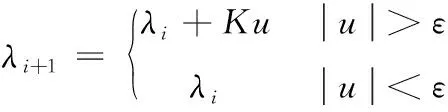
(14)
其中:λi为拉格朗日乘子;ε为容差;K为接触刚度;u为接触间隙。
2 电枢装填过程分析
为了改善电枢与轨道之间的接触性能,本研究中采用凸轨道与电枢的配合形式并进行过盈装配,这就要求网格质量足够高。为了保证计算精度,使用8节点六面体单元进行网格剖分,并在电枢与轨道接触面、轨道外表面电流集中区域进行网格加密处理。基于发射器几何结构的对称性,在剖分网格时采用拉伸和映射的方法保证了网格的对称性。由于采用了边界元方法,因此不需要对空气区域进行网格剖分。网格剖分结果如图3所示。
图3 发射器网格剖分Fig.3 Mesh of the launcher
电枢的装填方式包括填塞式、紧固式等,根据冯登、国伟等[11-13]的研究,不同的装填方式对装填结束后电枢的状态影响不大,但装填过程中的推力偏斜可能改变电枢与轨道的接触压力。本研究中采用尾推式装填方式,即使用推杆将电枢从炮尾挤进,认为装填过程中推杆无偏移。图4所示为装填结束后电枢的变形情况和应力分布。可以看出,电枢区域变形量呈现明显的规律性:电枢臂尾端变形量明显大于电枢臂头部,由电枢臂尾端至电枢臂头部变形量均匀减小;而在电枢臂同一水平位置上,变形量基本相同。从图4(b)中可以看出,该电枢经装配后应力主要集中于电枢喉部,该区域最大应力未超过材料(6061铝合金)屈服极限(330 MPa),且留有一定余量,因此可以保证电枢的结构不出现塑性变形和破坏。
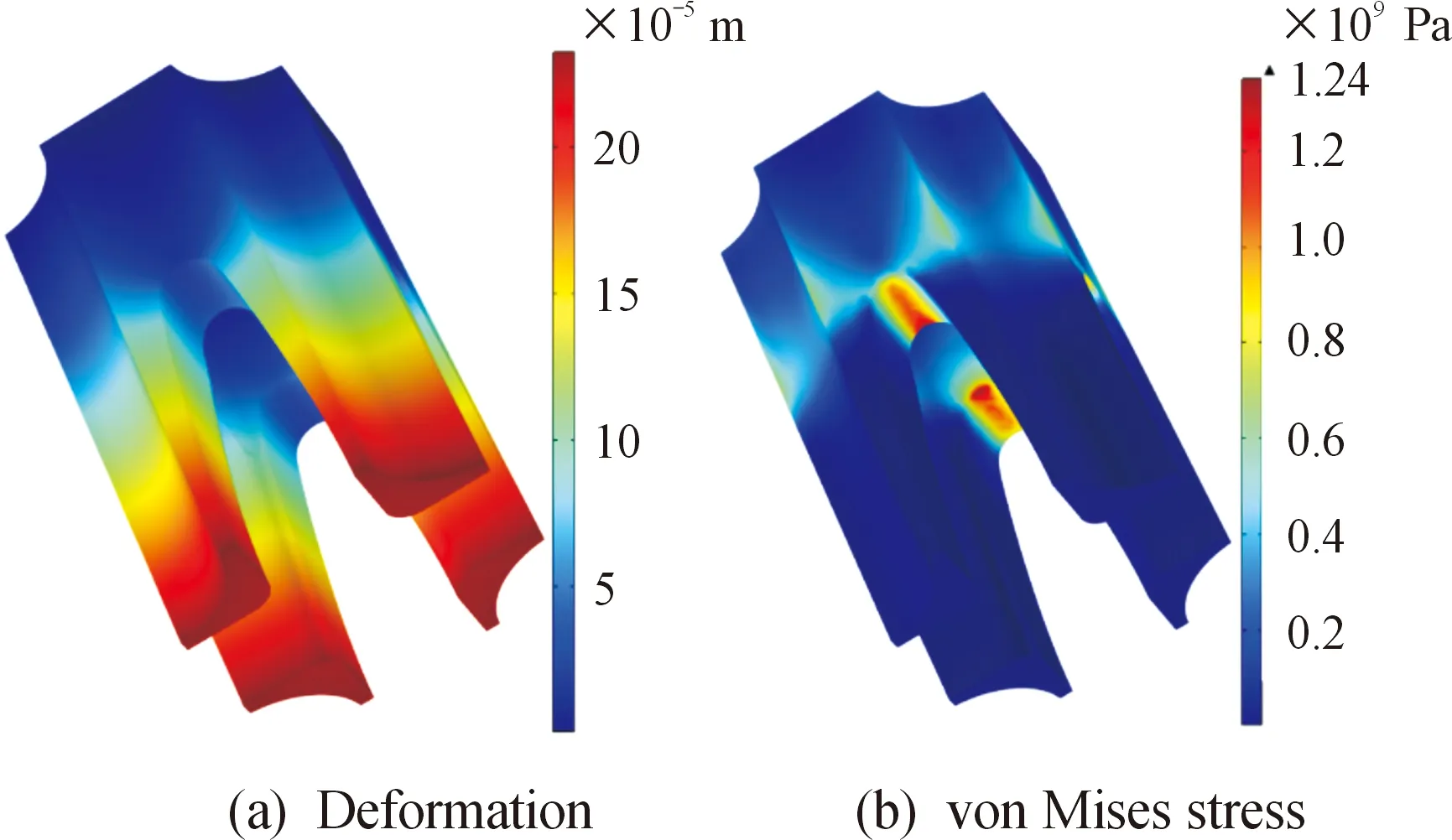
图4 装填后结构场仿真结果Fig.4 Results of structure simulation
尽管轨道的刚度远大于电枢,但其在装配过程中也会发生变形。图5所示为装配完成后电枢与轨道所在位置相对初始位置的变化情况。显然,其中阴影区域出现接触分离现象。
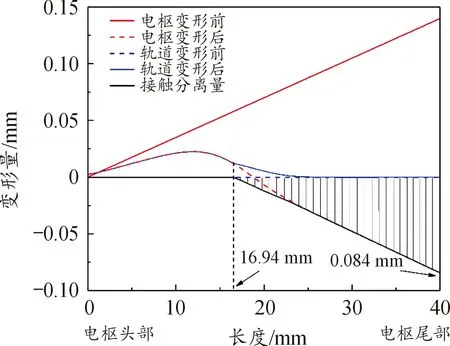
图5 电枢装填后变形情况Fig.5 Deformation of the armature filling
从图5中可以看出,在进行初始装配后,电枢尾端变形量明显大于电枢头部,电枢臂头部向后16.92 mm处,电枢与轨道不发生接触,出现接触分离现象。接触分离时,电枢与轨道之间的最大距离达到0.84 mm。此外,从其中可以看出,装配过程中轨道受力变形,向内凹陷的最大凹陷深度达到0.09 mm,向外凸出的最大凸出量达到1.8×10-4mm,轨道不平度远超一般工业对接触面粗糙程度的要求。可以预见,这种程度的变形必然会对发射过程造成负面影响、导致轨道寿命缩短。因此,目前有研究者采用钢板对轨道内侧进行加强。
当前,制约电磁轨道发射装置走向实用阶段的一个重要因素是电枢与轨道之间恶劣的接触特性引起的轨道损伤。在工程中采用过盈配合的主要目的就是为了改善枢-轨接触特性。由于电磁轨道炮工作在高度非线性的瞬态条件,发射过程中实时测量接触情况相对困难,因此通过结构有限元仿真,对枢-轨接触压力进行研究就十分有必要。图6所示为初始装配后接触面上枢-轨接触压力分布情况。分析枢轨接触压力分布云图可以看出,在接触面上,接触压力主要集中于电枢臂中部偏上位置,电枢臂头尾两端接触压力较小。在水平方向上,两侧接触压力高于中心,且呈对称的蝶翼状分布。为了更清楚的展示接触压力的分布情况,取图示的两条路径绘制接触压力分布曲线。可以看出,最大接触压力位于棱边中部偏上位置,达到572 N;电枢臂对称轴上接触压力最大处位于整个接触区域接触压力最大值的同一水平位置上,达到259 N。在电枢头部向下16.94 mm以后,接触压力为0,表明该区域的接触状态可能为相互贴合但无接触压力或未发生接触。
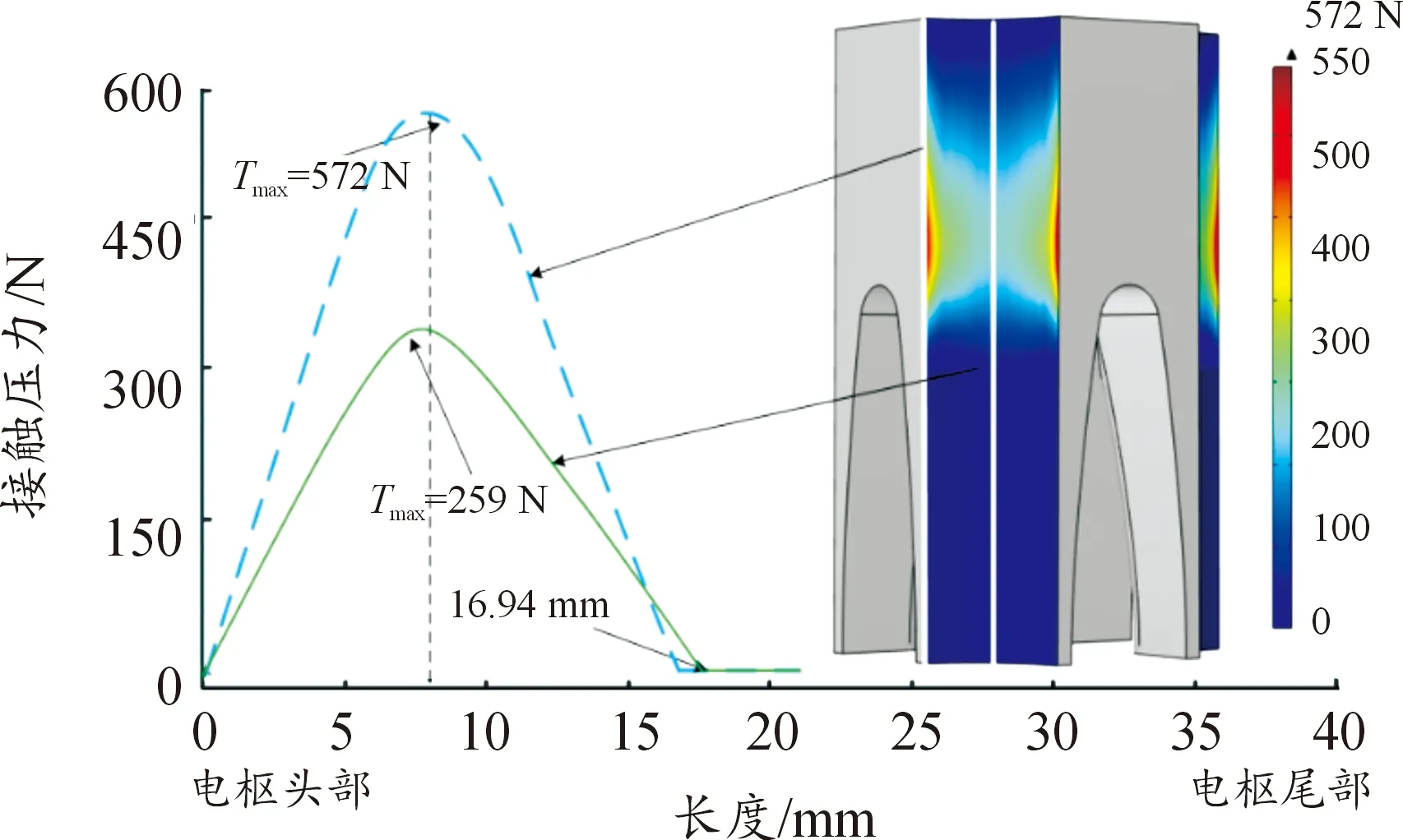
图6 接触压力分布Fig.5 Distribution of contact pressure
与图5对比可以看出,接触压力的分布情况与电枢、轨道变形情况相互吻合。在变形量分析指示的枢轨接触分离区域,接触压力也为0。这表明本文采用的分析方法和得到的结论比较可靠。
为了进一步分析电枢装填后的枢轨接触状态,对接触面上总接触压力Fcon各节点的受力进行了统计。通过全部节点接触压力的峰值Pmax和标准差SD分析接触压力分布的均匀程度;定义节点上接触压力大于0的节点为接触节点,节点上接触压力大于“1g/A”所需接触压力的节点为有效节点,统计了接触区域占比CA和有效接触区域占比ECA。
统计结果如表2所示。
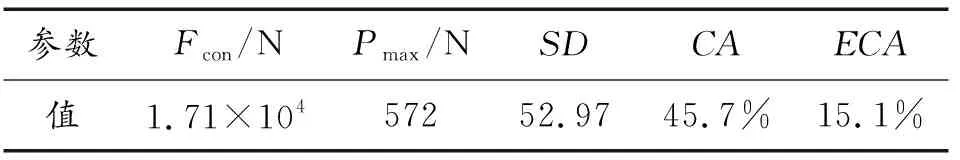
表2 初始接触参数统计结果Table 2 Paramaters of initial contact
3 发射器工作过程分析
电磁轨道发射器是一种能将电磁能与动能瞬时高功率进行转化的装备,因此发射器的受力情况是影响其效能的主要特征。但受电磁轨道发射器本身原理所限,发射器的受力与其电磁特性、接触特性、温度特性紧密耦合,难以通过理论计算得出精确结果。为此,有必要采用仿真的方法对发射器的受力情况进行研究。
3.1 电枢运动特性分析
电枢在运动过程中受到电磁推力、摩擦力、空气阻力和接触压力共同作用。根据实验,电枢所受空气阻力小于200 N,远小于电磁推力和摩擦力,因此可以忽略。因此得到电枢运动方程式为
(15)
其中:V为电枢区域;v为电枢运动的速度;ma为电枢的质量;f为电枢受到的摩擦力,f=μFN,μ为摩擦系数,FN为枢-轨接触压力。
本文采用峰值为400 kA、上升沿时间为0.02 ms的平顶脉冲电流作为激励,作为试验中分级储能激励电源的简化,原因在于这种简化可以更加清楚的观察发射过程中各种物理现象的变化而对结果影响较小。通过仿真,得到发射过程中电枢的运动特性曲线如图7所示。
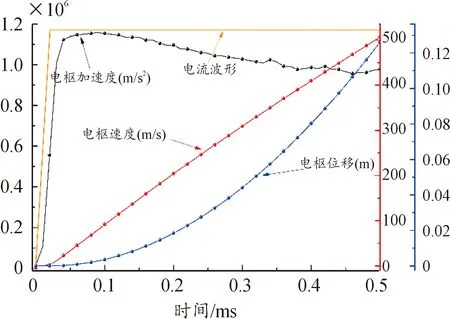
图7 电枢运动特性Fig.7 Movement of the armature
在脉冲大电流的激励下,电枢仅通过126 mm的加速段行程,就在0.5 ms内被加速至506.9 m/s的高速。在整个工作过程中,电枢速度平稳上升。在0.04 ms后,电枢加速度不再维持急剧上升的趋势;在0.09 ms后,电枢加速度达到最大值,开始缓慢减小。
从图7中可以看出,电枢加速度达到峰值的时刻晚于电流达到峰值的时刻。根据洛伦兹力公式,电枢所受推力与电枢上流过的电流和电枢后方接入回路的轨道上电流激发出的磁场有关,接入回路的轨道长度越长则电枢所受推力越大。图8所示为电枢静止于炮口附近时以电流为参数仿真和恒定电流条件下以电枢位置为参数仿真得到的结果。
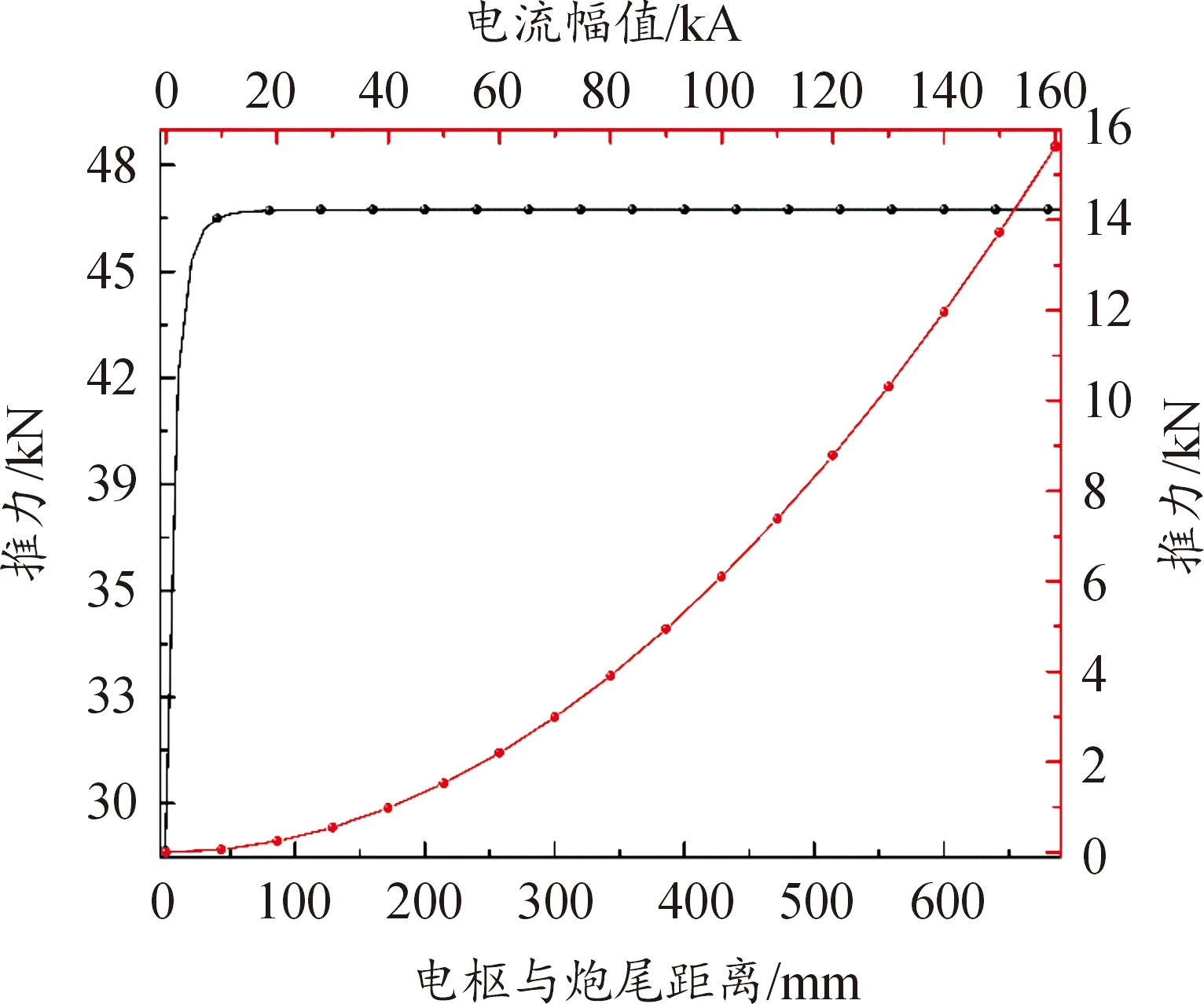
图8 电磁推力随参数变化情况Fig.8 Thrust of the armature vs parameters
可以看出,在不考虑电枢位置变化的条件下,电枢受力与电流幅值的平方成正比;电枢距离炮尾50 mm(2倍口径)以后,其所受推力基本不随电枢位置的变化而变化,这与王莹教授在普通双轨电磁发射器上发现的“四倍口径”规律略有差别,表明四轨电磁发射器的电枢初始安装位置比普通双轨电磁发射器要低。在炮身长度相同的条件下,四轨电磁发射器的电枢加速段距离更长,可以获得更好的性能。
对比图7与图8,还可以发现,恒定电流条件下,电枢远离炮尾后电磁推力基本不随电枢位置变化,而有限元仿真结果表明,电枢加速度达到峰值后会逐渐减弱。这是由于趋肤效应和速度趋肤效应改变了电流在轨道和电枢上的分布,使推力减小。
3.2 瞬态接触特性分析
枢-轨接触特性极大影响发射器性能,而且由于发射器工作状态变化剧烈,任意一个时刻的接触状态都不可持续,因此需要通过瞬态仿真对其进行研究。
图9所示为电枢所受接触压力随时间变化的情况和摩擦力与接触压力的比值、电磁压力与电磁推力的比值随时间变化情况。从图9中可以看出,电枢运动过程中受到的接触压力与电枢所受电磁推力变化趋势基本相同。分析电枢所受电磁压力与电磁推力的比值可知,电枢所受电磁压力与电磁推力的比值基本保持在0.65左右,受电枢运动、电流大小的影响不大,这与伊根博格斯的研究一致。仿真时,本文将枢轨间动摩擦系数设置为0.1,根据式(1),摩擦力与接触压力的比值即为摩擦系数,图8曲线中摩擦力与接触压力的比值基本不随时间变化,始终在0.1左右波动,最大误差仅为1.2%,这与仿真时的设置相吻合。该曲线在发射初始阶段出现剧烈增长的原因在于在该时刻,枢轨之间的接触状态由静摩擦转为动摩擦,发射器电流正在建立阶段,尚未稳定。
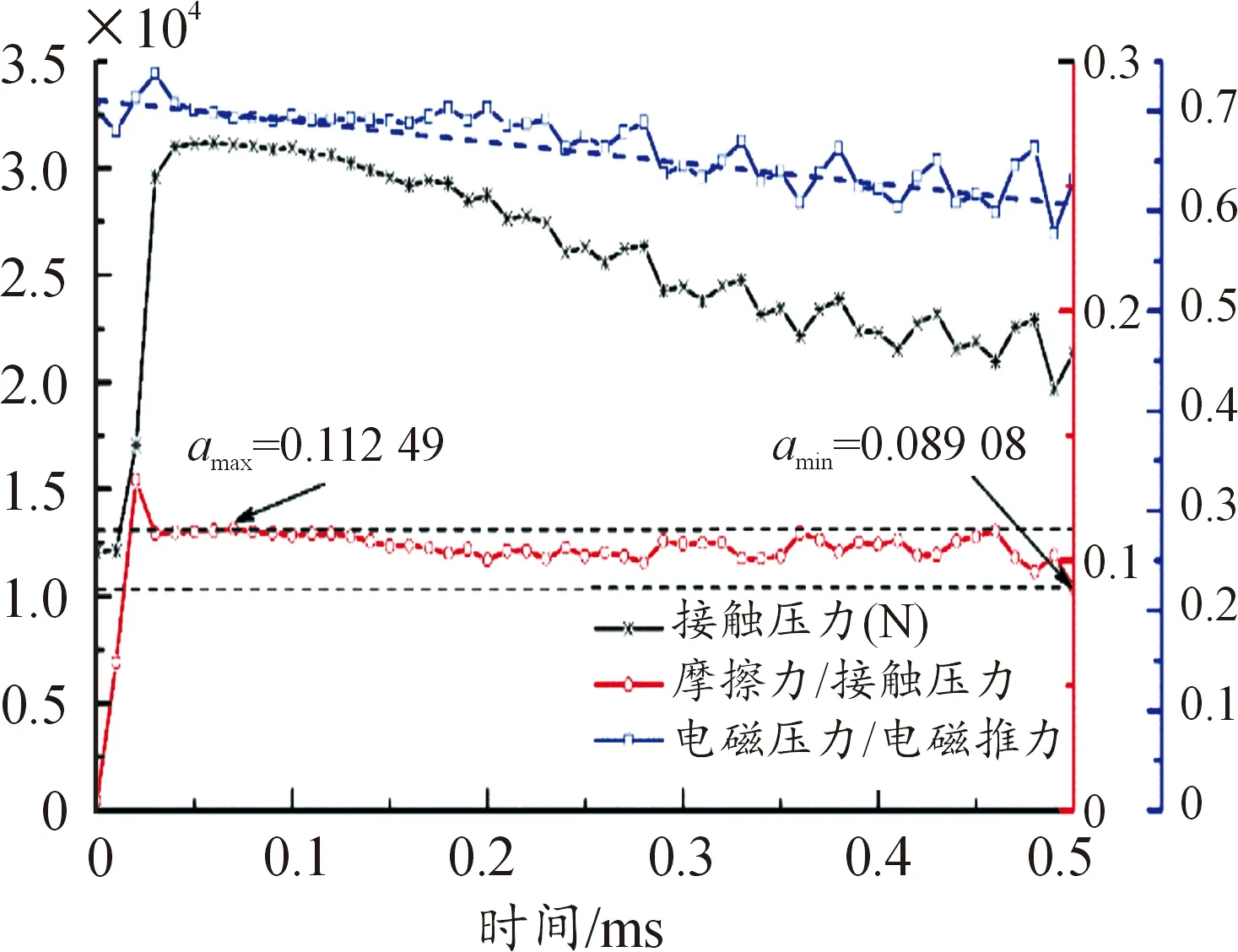
图9 枢轨接触特性Fig.9 Contact of the armature-rails
图10所示为发射过程不同时刻枢轨接触面上接触压力云图。
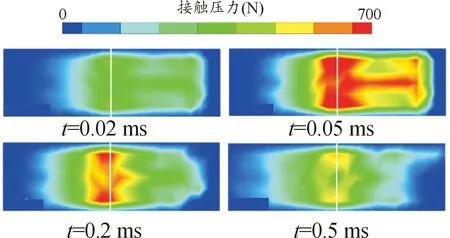
图10 接触压力分布Fig.10 Distribution of contact pressure
分析接触压力可知,总接触压力在0.06 ms达到峰值,随后开始减小;通电后接触压力分布规律与装填完成后接近,但随着总接触压力的增大逐渐向电枢尾端扩散。总体而言,通电后接触压力分布更加均匀。之所以会出现初始压力较大的区域电接触压力也相对集中的现象,是电磁场与结构场相互耦合的结果。CLM模型规定,接触压力越大的区域接触电阻越小。根据安培定律,电阻越小的区域电流密度越大,电流密度增大又导致接触压力增加。
图11所示为第二节定义的几个接触参数在通电情况下随时间的变化。可以看出,接触面上峰值接触压力Pmax、接触区域占比和有效接触区域占比随时间变化规律均与接触压力随时间变化规律类似:接触压力越大,则接触压力峰值、接触区域占比和有效接触区域占比均增大;而衡量接触压力均匀程度的方差则在通电后减小,随着接触压力的增大而增大,但始终不超过未通电时的接触压力方差。这表明通电后接触面上接触压力的分布会更加均匀,但电磁力引起的接触压力增大会导致接触压力集中。此外,从图中还可以看出,通电后,接触区域占比超过90%,有效接触区域占比在30%左右,这意味着接触分离现象逐渐消失,接触效率得到提升。分析接触压力峰值随时间的变化情况可知,尽管总接触力增大,但接触压力峰值变化并不明显,说明接触压力峰值区域受通电影响不大、总接触压力的增大主要体现在高接触压力区域面积的增加,这一现象也与云图的表现相符。
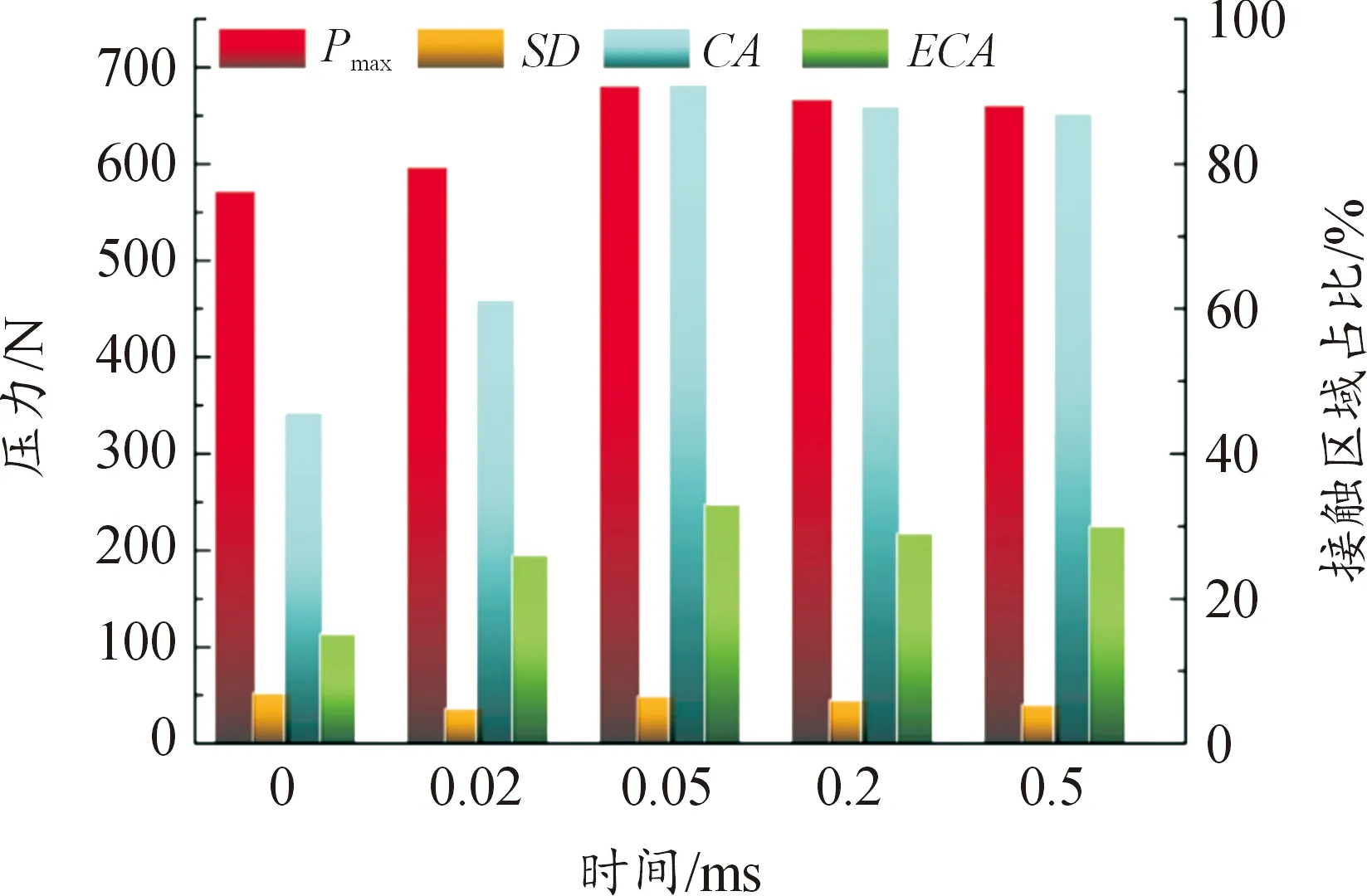
图11 接触参数随时间变化情况Fig.11 Contact parameters vs time
4 发射器多物理场耦合仿真分析
发射器工作过程中会出现趋肤效应、摩擦生热等多种涉及物理场耦合的现象,影响发射器性能,因此需要对发射器的电磁特性、温度特性进行研究。
4.1 电磁特性
图12展示的是0.02 ms时刻发射器电枢与轨道上的电流分布情况。可以看出,轨道上电流密度集中于轨道内表面和外侧尖角处,轨道中心电流密度较小,这一现象是由趋肤效应引起的。电枢上,电流密度远大于轨道上电流密度,表明焦耳热引起的烧蚀最有可能出现在电枢区域。

图12 0.02 ms时刻发射器电流密度分布Fig.12 Distribution of current density at 0.02 ms
图13所示为发射过程中不同时刻电枢区域电流密度分布。可以看出,电枢上电流密度主要集中于电枢喉部和电枢臂尾端。在枢轨接触面上,随着时间变化电流分布更加均匀,呈现出从电枢尾部向电枢头部扩散的趋势。CLM接触模型认为,接触压力越大的区域接触电阻越小,从图13中也可以明显看出,接触压力集中的区域电流密度较大,且随着接触区域和有效接触区域的增加,电流分布更加均匀,最大电流密度减小,电流集中程度有所缓解。此外,图13中电流密度最大值位于电枢臂尾端,这一现象可以通过安培定律和速度趋肤效应解释。安培定律规定,电势差相同时电阻越小则电流越大,也就是说电流将更多集中于电阻更小的区域和路径。由于电枢的电导率远大于轨道,因此电流将集中于电枢臂尾端。速度趋肤效应理论表明,电枢运动速度越大时,电流将更多地被“拖曳”向电枢臂尾端。
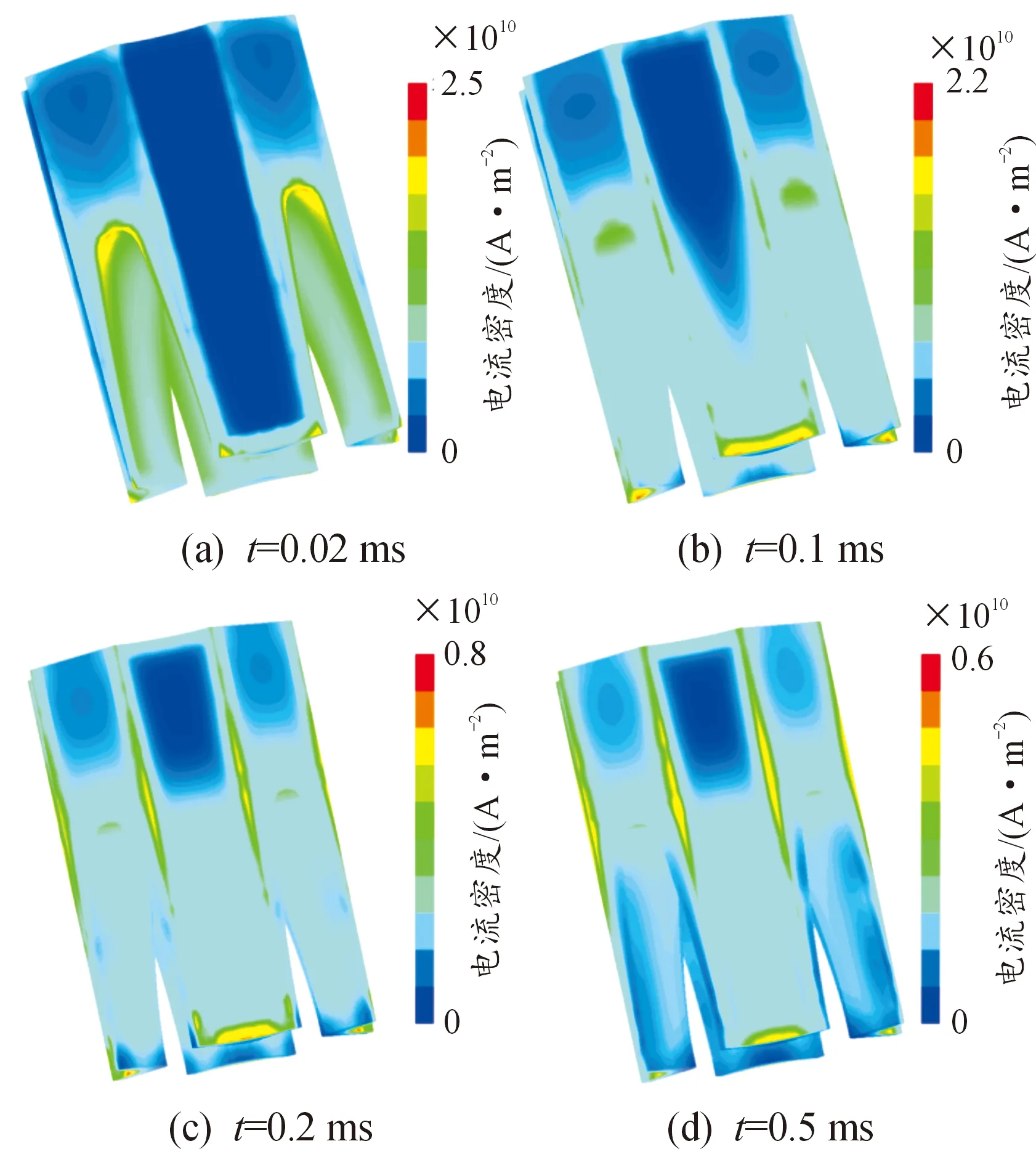
图13 不同时刻电枢区域电流密度分布Fig.13 Armature current density at different time
图14所示为电枢喉部电流密度分布情况。可以看出,在0.01 ms和0.03 ms时刻,电枢喉部电流密度大于电枢臂尾端电流密度;其后,电枢臂尾端电流密度增长,大于喉部电流密度,这一现象也可以通过速度趋肤效应解释。但整体上,随着时间的推移,电枢区域电流密度减小。
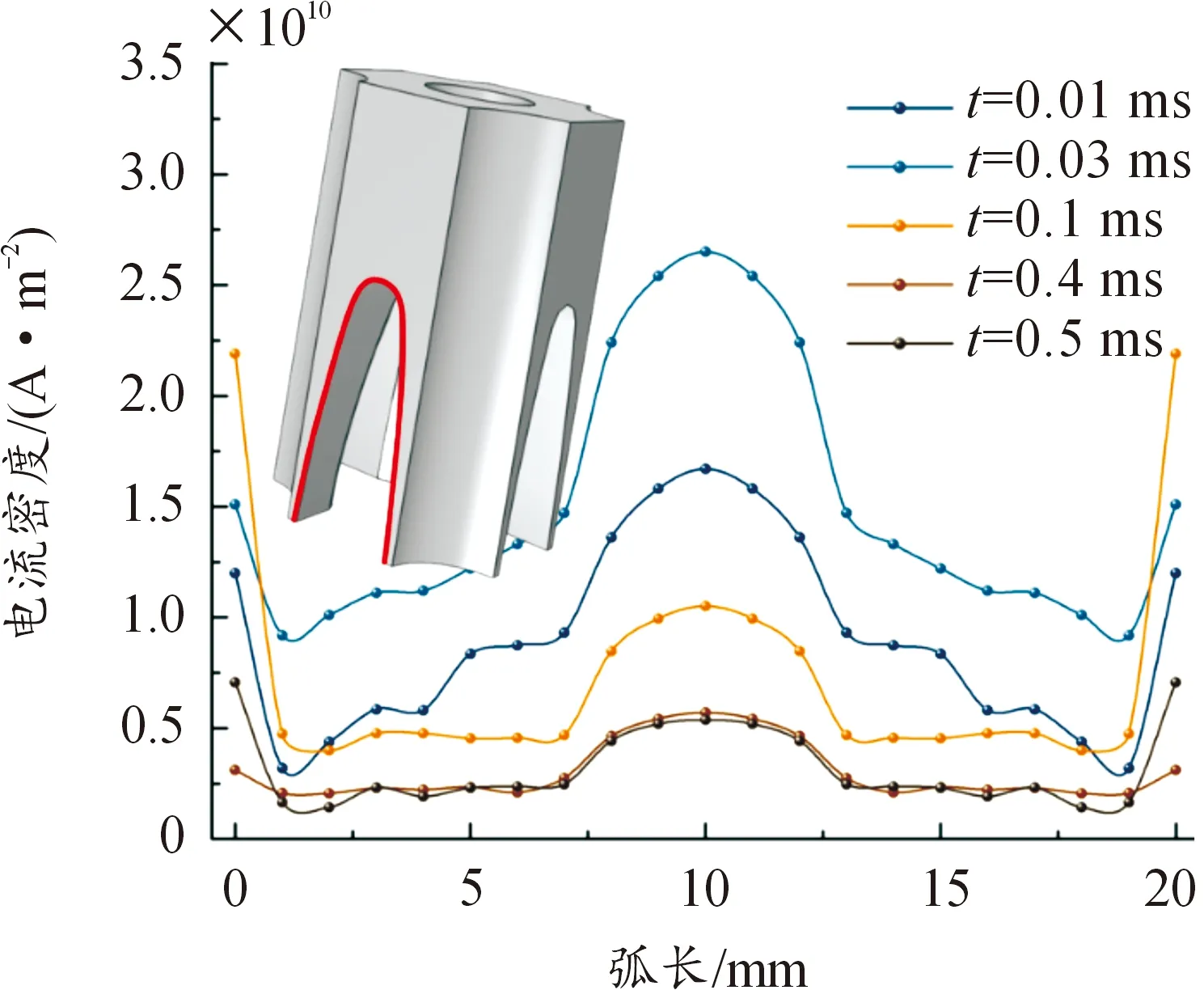
图14 电枢喉部电流密度分布Fig.14 Distribution of current density at the throat of armature
图15所示为四轨电磁发射器膛内磁感应强度分布,图15(b)中的3个截面分别位于炮口后方200 mm(截面1)、电枢喉部向后5 mm(截面2)和炮尾前方20 mm(截面3)。可以看出,四轨电磁发射器磁场强度主要集中于电枢后方较短的一段轨道附近,在电枢前端,磁场强度几乎为零;此外,发射器膛内形成了圆柱形的磁场屏蔽区域;在电枢后侧,膛内中心区域也保持了较好的磁屏蔽性能。
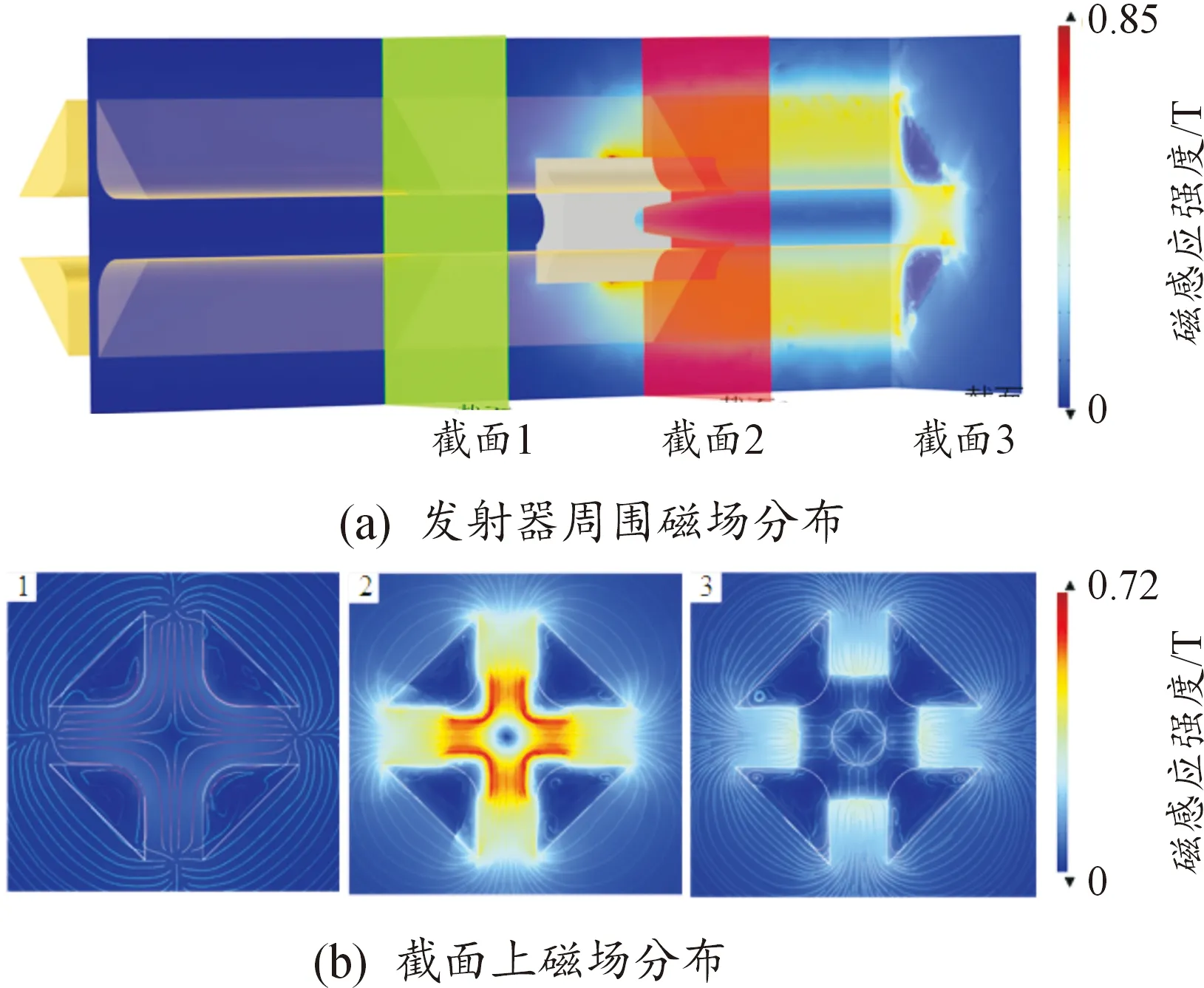
图15 发射器周围磁场分布Fig.15 Magnetic field distribution of the launcher
4.2 温度特性
当前,制约电磁轨道发射器走向应用的最大问题在于轨道的寿命问题。轨道的损伤形式主要有刨削、烧蚀等,这些损伤与轨道的温度息息相关,因此有必要对发射器的温度特性进行研究。
图16所示为发射过程中不同时刻发射器温度分布。可以看出,在发射过程中的不同时刻,电枢上温升现象主要出现在电枢喉部、电枢臂尾端和电枢臂外侧电流密度集中的区域。总体而言,电流密度越大的区域温升现象越明显。对比图13与图16,一个明显的区别在于电枢臂表面电流密度较大而温升现象并不明显,原因在于温升是随着时间累积的,当前时刻的温度是前序所有时刻焦耳热共同作用的结果;而电流密度则不具有累积效应,当前时刻的电流密度与前序时刻无关。由于电流密度是随着时间逐渐由电枢臂尾端向电枢头部扩散的,因此越靠近电枢头部的区域温升的时间累积效应越不明显,温升也就越小。
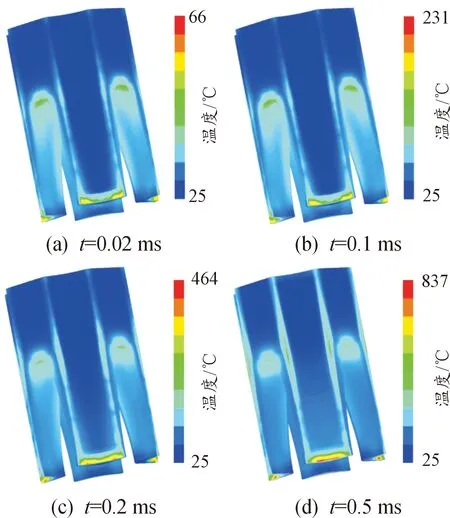
图16 不同时刻电枢温度分布Fig.16 Temperature distribution of the armature at different time
对比图14与图17可以看出,路径上的温度分布始终保持电枢臂尾端大于电枢喉部的规律,而电流密度分布在0.01 ms与0.03 ms时喉部大于尾端,其后则尾端大于喉部。出现这一现象的原因在于,随着电枢运动速度的增加,速度趋肤效应更加明显,电流将被“拖曳”至电枢臂尾端。若不考虑摩擦热的影响,那么路径上温度分布与电流分布应始终保持一致,但由于摩擦热主要集中于电枢臂尾端(电枢臂尾端过盈量最大),改变了路径上的温度分布,使电枢臂尾端温度高于电枢喉部。
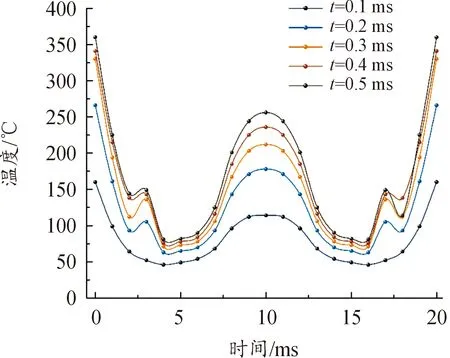
图17 电枢喉部温度分布Fig.17 Distribution of temperature at the throat of armature
5 结论
通过构建瞬态电磁-热-结构耦合有限元-边界元仿真模型,对四极凸轨道电磁发射器的动态发射过程进行了研究,分析了发射器的枢轨接触特性和膛内多物理场耦合现象,得到以下结论:
1) 电磁轨道发射器电枢所受推力与电流幅值、发射器结构和电枢初始装填位置有关。相比双轨电磁发射器,四轨电磁发射器的电枢在距离炮尾2倍口径距离的位置装填即可获得峰值推力,电枢加速性能更佳。
2) 发射器工作过程中电磁场与结构场的耦合关系体现在:通电后,电磁力迫使电枢压向轨道,增大了枢轨之间的接触压力并使接触压力的分布更加均匀,进而改善了发射器的接触状态;接触压力的作用又减小了电枢与轨道之间的接触电阻,并改变了接触面上的电流分布。
3) 发射器工作过程中电磁场、结构场对温度场的影响体现在,焦耳热与摩擦热的共同作用引起了发射器的温升:电流集中引起的焦耳热更多地使电枢喉部和电枢臂尾端温度升高,枢轨接触引起的摩擦热更多地使电枢臂尾端温度升高。二者共同作用下,电枢温度分布出现了发射初期电枢喉部温度较高,发射后期电枢臂尾端温升明显的现象。
本文的研究对认识电磁轨道发射器的多物理场耦合机理和电磁轨道发射器的结构设计具有一定参考意义。

