机器学习在航天结构载荷逆向识别中的应用研究
郭晨宇,蒋亮亮,张 希,杨 帆,阳志光
(北京宇航系统工程研究所, 北京 100076)
0 引言
载荷识别方法最早于20世纪70年代中期,在航空领域中由Bartlett和Flannelly提出[1],是指利用测量的响应,如位移、速度、加速度、应变等,凭借已知的结构特性来反演结构载荷。载荷虽然可以由传感器测得,但能得到的往往是局部信息,在一些复杂工况且结构敏感部位处的载荷往往无法直接测量[2]。载荷识别可以由有限的响应逆推结构上整体的受载情况,并监测载荷变化是否会达到破坏阈值,甚至使结构做出调整,从而降低危险区域处的负荷,这对结构轻质化设计、智能化设计、结构长时间服役的健康监测有重要的工程实用价值。
载荷识别经过数十年的发展,已经有了长足的进步。国内外的一些学者如周盼[3]、Sanchez[4]等,先后从频域法和时域法分别介绍了载荷识别的相关方法,Ruixue Liu[5]对频域法和时域法进行误差分析,并介绍了载荷识别中处理不适定性和非线性问题的各种方法。针对不确定性结构,杨智春[6]介绍了概率模型、模糊模型等多种数学模型,对结构系统进行描述,从而识别载荷。
众多求解载荷过程都包括建立系统模型和求解系统模型2个过程。但是实际结构通常十分复杂,难以建立解析解模型,建立有限元模型的识别精度也往往不高;求解模型时会面临非正定性和病态性难题,虽然可以通过增加约束条件、优化测点和采用正则化方法[7-8]来解决,但是其条件和参数的选取往往较为困难。李金良[9]在识别动车构架上载荷时,对载荷解耦,标定单一载荷与动应力之间的传递关系,依据叠加原理得到多载荷与响应之间的传递系数矩阵,并通过严格选取测点,避免矩阵求逆时的病态性与非正定性;高云霄[10]在此基础上,通过正则化方法中的截断奇异值避免了载荷解耦和测点选取,直接利用测点响应识别构架载荷,但仍需要标定传递系数矩阵,构建系统模型。
采用机器学习方法进行载荷识别[11-12],可以跳脱系统模型的约束,基于大数据直接从中找出载荷-响应的映射关系,Zhou[13]通过训练包含长短时记忆层的深度递归神经网络,识别出作用在非线性复合材料板上冲击载荷的历程;夏鹏[14]利用时延神经网络,通过输入倒序动响应,在时域内识别作用在飞机舵面上抖振载荷的历程。机器学习依赖于大量训练数据支持,然而现实情况中数据往往不足,尤其对于航天大型复杂结构,通过试验获取数据成本高昂,限制了机器学习的应用。
目前,载荷识别方法在实际复杂工程领域中的应用相对较少,仅适用于较为简单的结构形式和载荷类型。采用机器学习方法,逆向识别典型航天复杂结构上相互耦合的载荷。训练合适的机器学习模型需要大量的载荷-响应数据,而有限元仿真是以低成本提供数据支持的最佳手段。对目标结构建立仿真模型,结合少量真实试验数据评估仿真模型,做出修正,实现高保真仿真建模;接着基于高信息熵对传感器测点布局优化,提取主要特征,减少测点的数量,保证数据的大规模和高质量性;由获得的数据训练出适合于当前结构的机器学习模型,实现结构载荷逆向识别。
1 载荷逆向识别方法
1.1 结构高保真建模仿真分析技术
仿真建模是以较低成本获取大规模高精度“载荷-响应”数据集的唯一手段,但仿真值与真实试验值会存在一定差异。两者的差异一方面来自于实际结构加载试验中测量的偏差;另一方面是由于仿真模型无法完全替代实际结构,尤其对复杂非线性连接部位处建模时,采用不同的等效替代模型或者接触条件,会得到不同仿真结果。选择等效模型和接触条件从而修正模型达到高保真,实质上是一个优化问题,优化列式如下:
Find {θM},M=M{θ,F}
min |S{F}-M{θ,F}|
s.t.θM>0
(1)
优化目标是在外载F作用下,使得仿真模型响应M与真实结构响应S的差值目标函数最小,其中θM是建立仿真模型M时的待优化参数。目标函数往往是非线性的,并且有多个局部最优解。如何有效地跳出局部最优点而到达全局最优点对修正结果的好坏至关重要。
借鉴生成式对抗网络(GANs)[15]的思路,采用对抗代理模型对仿真模型进行优化修正。针对变量规模大、响应函数复杂的问题,利用代理模型方法[16-17]构建2种不同拟合形式的初始生成模型G和判别模型D。G模型首先给出未知设计的预测值,D模型对其进行判断,模型间相互迭代,实现在有限样本条件下,建模精度的最大化。构建迭代过程中对抗学习函数的公式如下:
(2)
L1与L2为D模型的判别函数,用于区分真实样本与模拟样本,取值偏向于1表示D预测该点贴近真实值,取值偏向于0表示D预测该点远离真实值;Z为随机测试集,用于表征模型在全局的预测精度。优化列式分别对G与D的超参数进行优化。G的优化目标为对于随机测试集Z的预测值能够通过D的检测。
理想情况下,对抗模型能够达到均衡,即优化列式上的鞍点[18]。然而由于2个模型无法同时达到最佳状态,会在迭代几次后陷入振荡,始终保持一个模型精度高、另一个模型精度低。因此只要自动筛选出较好的模型即可,不用2个模型都收敛到最佳状态。三重指标方法考虑了初始样本检查、迭代学习函数方向与最大似然估计法,分别对2个模型进行比较:
1) 初始样本检查。比较G与D模型对初始样本信息预测值与实际值的均方根误差,选择误差更小的一方指标记为1,否则记为0。
2) 迭代学习函数方向。对抗准则分别要求G的最大化与D的最小化,计算该迭代步2个模型的学习函数值增量,若符合该模型的优化方向,则该指标记为1,否则记为0。
3) 最大似然函数估计。由代理模型Kriging方法[19-20]得到2个模型的最大似然函数,数值较大的一方指标记为1,否则记为0。
当3个指标计算完成后,选择指标总和较大的模型作为最终模型。三重指标法综合了多种考量,能够稳定得到较优模型。
1.2 高信息熵测点布局优化
实际结构复杂多样,测点要能够最大程度准确获取需要的信息。结构边缘部位和内部连接非线性区域容易造成测量的偏差;且在应力水平较低和变化梯度较大的地方,测量相对误差也比较大,如图1所示。因此在布置测点时,应首先规避上述部位,布置在应力水平高、变化相对平稳的地方。
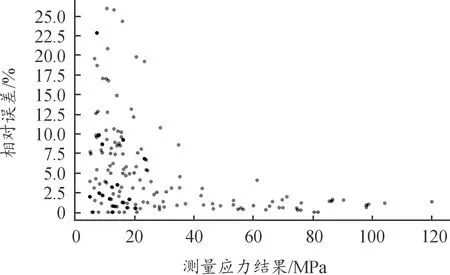
图1 相对误差随载荷变化情况Fig.1 Relative error changes with load
由传感器测点信息逆推外部载荷往往面临着病态和不适定问题,但如果布置测点的数量过多会严重影响计算的效率,增加成本和系统的复杂度,降低可靠性。这在以轻质化和可靠性为重要指标的航天器结构设计中,是无法接受的。在载荷识别系统中,期望用最少的传感器准确反映结构尽可能多的信息,因此开展基于高信息熵的测点布局优化。
首先确定优化目标。由于很难通过实测飞行得到载荷-响应数据,因此具体优化目标为“仿真模型外载荷识别的准确度”。考虑到仿真模型与实际结构间的差距,构建优化算法时,应充分考虑二者间的区别。
其次建立优化准则。准则包含4点:测点数量最少,测点对外载荷敏感,噪声环境下的鲁棒性强,测点间具有互检性。
1) 测点数量最少
测点的数量认为与质量直接相关,希望以最少的测点得到满足载荷识别需求的信息量,这个问题可以等效为机器学习中特征提取问题。假设原始样本有n个载荷工况:Y=y1,y2,…,yn,有m个测点:X=x1,x2,…,xm。经过正交变换,综合得到m个变量ci:
(3)
并且满足:
(4)
由样本X的相关系数矩阵R,用雅克比方法,求特征方程的根:
|λI-R|=0
(5)
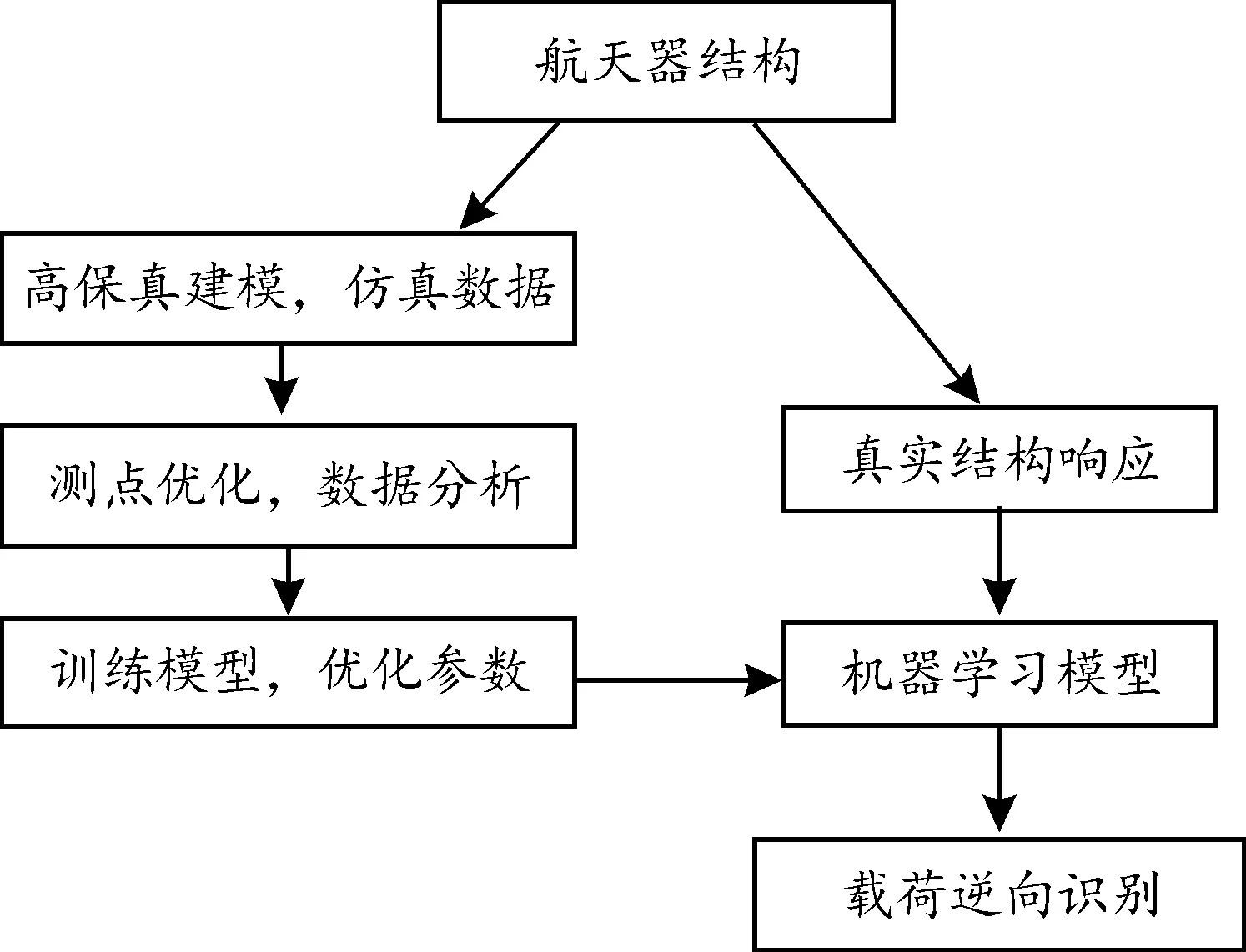
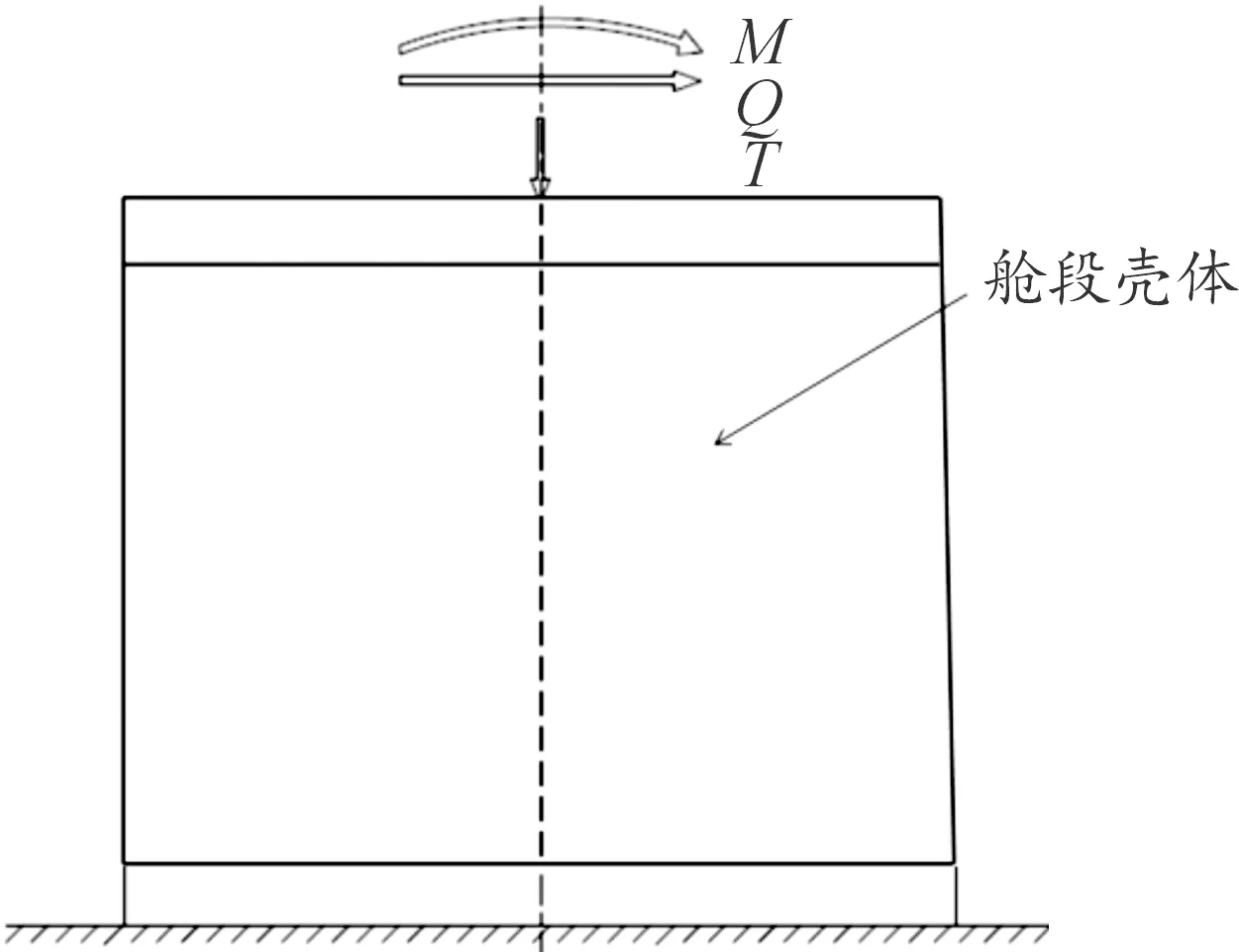
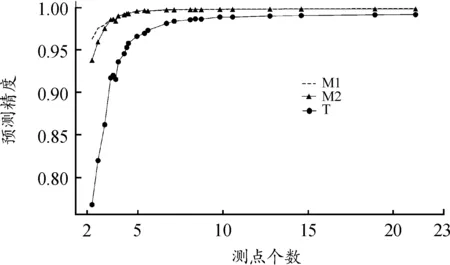
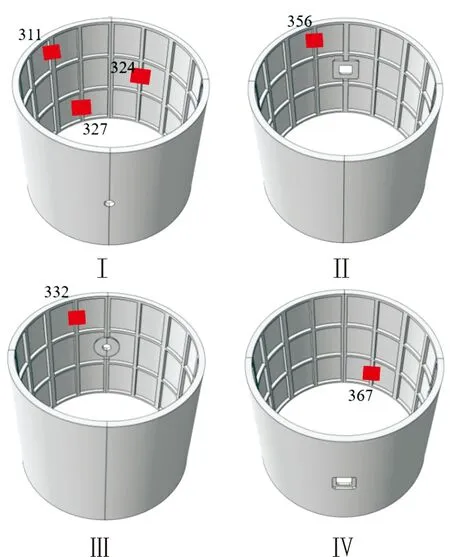
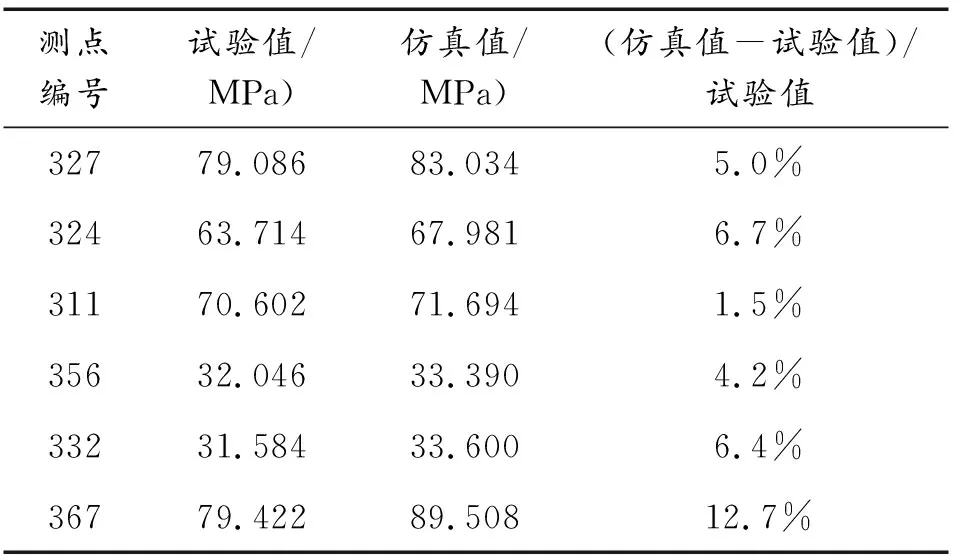
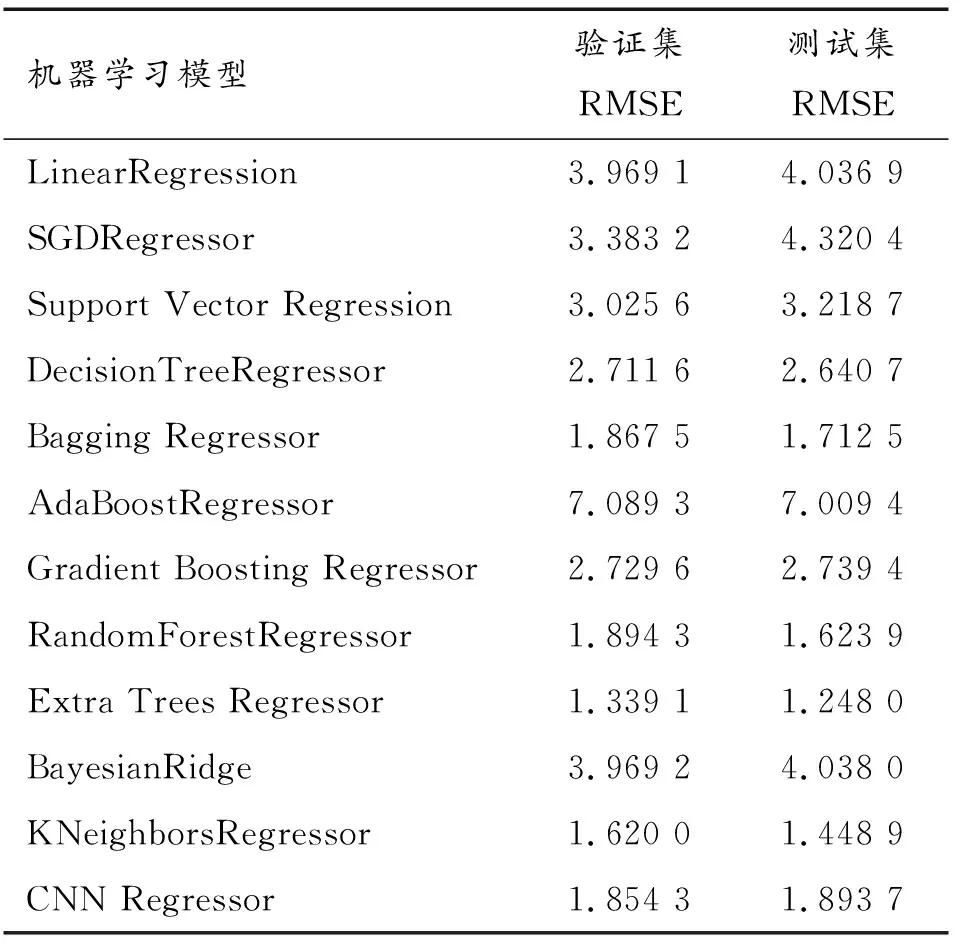
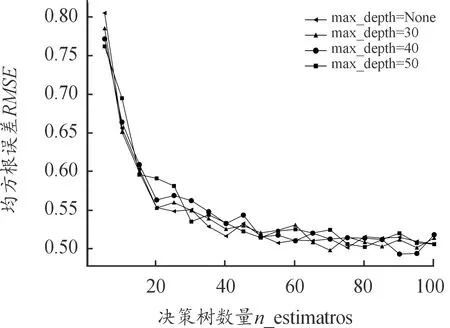
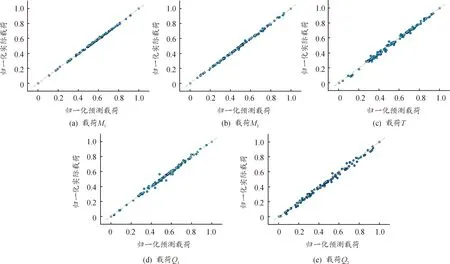
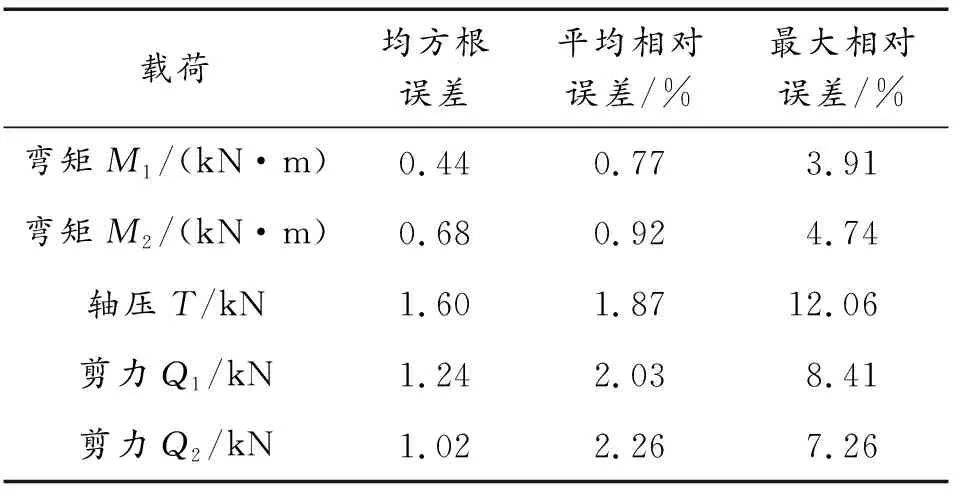
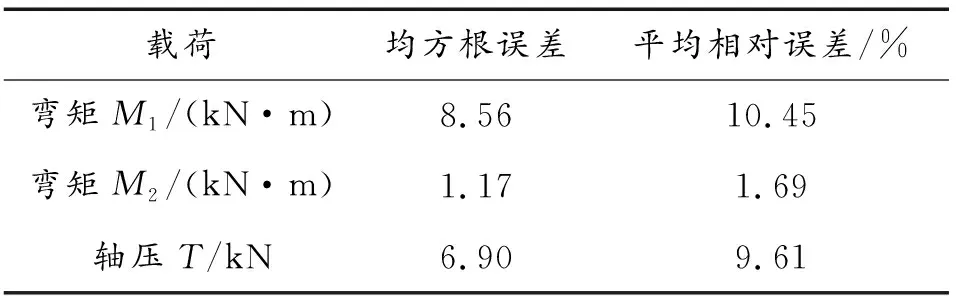
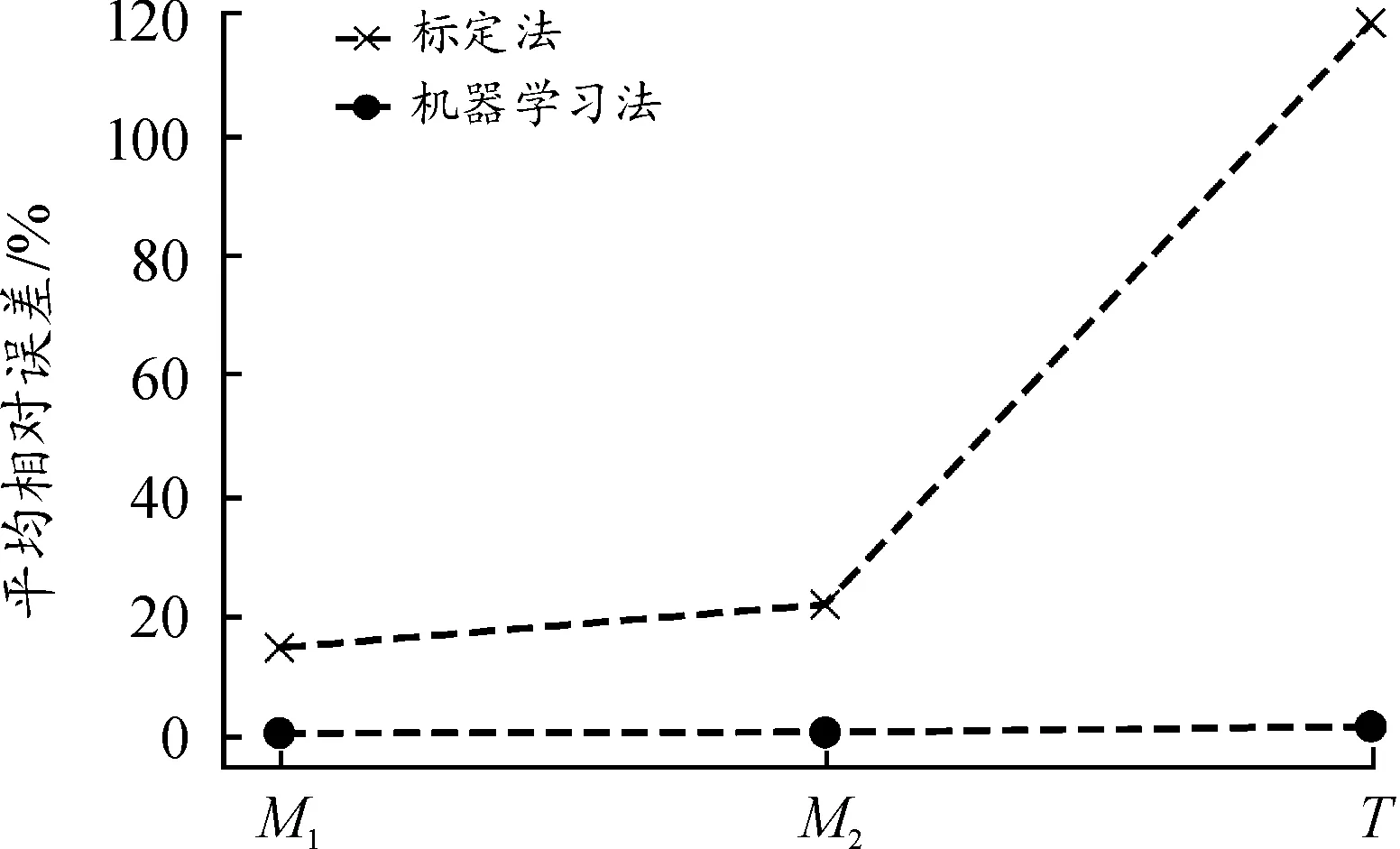
即样本相关系数矩阵的n个非负特征值。对特征值进行排序,从中提取综合变量X的前k(k (6) 图2为某问题待预测7个变量的累计方差贡献率和特征的累计方差贡献率。可见,待预测的7个变量完全不相关,而特征间的相关性较大,3个特征的累计方差贡献率即达到99%,说明该组特征的鲁棒性不强,易受噪声干扰。 图2 某问题待预测量与特征量的累计方差贡献率Fig.2 Cumulative variance contribution rate of the quantity to be predicted and the characteristic quantity 2) 测点对外载荷敏感 应变信息对外载荷的敏感可以转化为应变信息与外载荷间的相关性。应变信息与外载荷相关性高,说明外载荷对该测点处应变的影响程度大。常规贴片方式一般会导致测点间的信息大量重复,构建相关性热点图判断测点间的相关性程度,制定一个综合指标: (7) 式中:R为计算2个量的相关性函数,K为从测点群中选取测点的数量,M为待预测载荷数量。故式中分子表征测点与载荷间的相关性,分母为测点间的相关性,最大化指标f,可以获得与载荷相关性较大、测点间相关性较小的测点集合。 3) 噪声环境下的鲁棒性 在构建训练数据时引入偏差来提高对噪声的鲁棒性,一般采用随机变量替代确定性变量,比如在仿真得到的训练数据中添加高斯白噪声。具体变量分布模型及方差需要引入领域经验。 4) 测点间互检性 测点间的互检性可以通过引入新的评定变量实现:假设有n个测点X=(x1,x2,…,xn),引入变量K=(k1,k2,…,kn)加入训练数据。其中kj表征xj是否异常,取值为0或1。构建训练数据集时,随机选取一定比例的xj,将其给定为任意值,表征该测点完全错误,同时将相应的kj定为1,其余测点定为0。 根据上述方法,搭建出测点布置优化流程如图3所示。 图3 测点布置优化框架Fig.3 Optimized framework for sensor layout 具体步骤如下: 步骤1随机生成载荷F,并以此为基础生成带偏差载荷F′,进行仿真计算,选出响应较大的n个测点;循环g次,获取g组训练集。 步骤2对测点进行方差和均值分析,确保响应对外载荷敏感。 步骤3根据坐标值和应力值对测点进行聚类,每个聚类选择一个测点,测点数量减少至K个(K 步骤4测点间相关性分析,相关系数大于p的并为一组,选取组内方差和均值最大的前t个测点作为相关测点对。 步骤5随机选择a%的测点作为异常值得到X′,并引入表征变量K。 步骤6输出[X′,(F′,K)]进行机器学习训练。 上述流程中相关参数的选取,通过利用领域知识和充分试验进行确定。 获取到数据量充足且贴近真实工况的“载荷-响应”数据后,采用机器学习方法对复杂航天器结构进行载荷识别,可以跳过力学上繁琐的机理分析,直接寻找载荷与响应之间的映射关系,对结构上载荷做出精准的识别。 由响应预测载荷数值在机器学习中属于回归任务。考虑到不同结构形式的载荷-响应之间存在多种映射模式,因此可以将训练数据按照一定比例,随机划分为训练集和测试集,通常训练集占训练数据的2/3~4/5,用于训练多种机器学习模型,剩下的为测试集,用于对各个模型进行评价。评价方式可以采用模型预测值与实际值的均方根误差RMSE: (8) 式中:y(pred)为预测载荷;y(true)为实际载荷;n为测试集数量。 均方根误差小,代表模型学习性能优异,可以良好地拟合训练数据,但也存在对训练数据过度的拟合,应用于真实载荷的预测,即泛化时,误差增大的风险。可以采用交叉验证的方法,进一步将原有训练集分割为新的训练集和验证集,在训练集上训练模型,在验证集上评价模型的学习性能,最后在测试集上对模型的泛化能力进行评价。例如5-折交叉验证,就是将训练数据分割出测试集后,再进一步分割成均等5份,每次取其中4份训练模型,剩下1份验证模型,将5次验证集上误差均值作为该模型学习性能的判断。 综合在验证集上学习性能和测试集上的泛化能力,从中筛选出最适合于对当前结构载荷逆向识别的机器学习模型。选定机器学习模型后,对模型超参数优化,可以进一步提升学习性能。网格搜索方法是对各超参数进行数值组合,通过交叉验证,寻找出一组最优的超参数组合。基于机器学习实现航天结构载荷逆向识别的完整流程如图4所示。 图4 航天结构载荷逆向识别流程框图Fig.4 Process of reverse load identification on aerospace structure 某航天器舱段壳体为网格加筋结构,在飞行过程中主要承受来自端部的弯矩、剪力和轴压载荷,如图5所示。除内部有网格加筋,该结构侧面还存在连接孔,结构形式复杂,非线性程度高,且轴弯剪载荷相互耦合。 图5 舱段壳体加载示意图Fig.5 Loading diagram of cabin shell 针对该结构开展高保真建模仿真、测点布局优化,基于机器学习方法进行载荷识别,并与传统的标定传递系数矩阵方法,进行比较。 对舱段壳体有限元建模,有限元模型包括上、下模拟边界,网格加筋壳体,上端框螺栓和钢套。结合少部分真实试验数据对模型进行优化,并在螺栓及其连接件处进行局部网格细化,模型共有48.9万个节点,28.9万个单元。 结构试验件初始布置120个测点,其中在各个纵向筋条区间长度的中心位置共有58个测点。由测点布局优化方法,从测点中挑选出较优的测点组合。开展多个工况下的加载试验,对各个测点的数据提取特征,得到载荷识别精度与测点个数间的关系如图6所示。可见,当测点数量大于6时即可较好地预测截面载荷。 图6 载荷识别预测精度与测点个数关系Fig.6 The relationship between accuracy of load identification prediction and the number of sensors 设定测点数量为6个,对原始测点布局优化,得到测点所在的位置如图7所示,优化测点在4个象限的分布位置较为均衡。 图7 布局优化后的测点位置Fig.7 Location of sensor after layout optimization 对比测点在某工况下的应力测量结果和有限元仿真分析结果。各测点拉应力的仿真值与试验值数据对比汇总如表1所示,仿真值与试验值在367测点处最大相差12.7%,在其他测点处相差均不超过7%,表明仿真建模具有高保真度。 表1 设计载荷下仿真值与试验数据对比Table 1 Comparison of simulation value and test data under design load 对舱段壳体的高保真模型开展批量有限元计算,得到在多个轴弯剪载荷作用下6个测点的应力响应,获得充足的“载荷-响应”数据集。对多种机器学习模型进行训练,训练数据共包含5 549个载荷-响应工况,其中80%作为训练集,进行5-fold交叉验证;20%作为测试集,对各个模型的预测性能进行评价。模型在验证集和测试集上预测载荷与真实载荷的均方根误差RMSE如表2中所示。 表2 机器学习模型训练结果Table 2 Training results of machine learning models 算法相对简单的线性回归模型(LinearRegression、SGDRegressor)对载荷-应力响应之间复杂的映射关系拟合程度不够,预测效果相对较差;支持向量回归模型(SupportVectorRegression)在测试集表现不如验证集,可知存在过拟合现象,且计算时用到了核函数,当数据特征和数据量增大时,计算效率下降;基于神经网络结构的CNN、KNN模型虽然功能强大,但却只基于数据出发,忽视了特征之间的紧密因果关系,且模型的参数众多,可解释性不强;以决策树为基础的模型在此次载荷识别任务中表现良好,做出决策的可解释性也强,甚至可以完全拟合数据,容易对训练数据过度拟合;极端随机树模型(ExtraTreesRegressor)集成学习了多棵决策树,且训练过程相较于随机森林模型(RandomForestRegressor)更加随机迅速,因此适合此次载荷识别任务。 初步选定模型后,采用网格交叉验证方法对模型的超参数“决策树数量n_estimators”、“决策树最大深度max_depth”做更细致的优化。优化效果如图8所示,模型预测载荷的均方根误差从1.339 1降到了0.493 4。迭代训练出最优的极端随机树模型后,将其应用于实际结构的载荷识别。 图8 机器学习模型参数优化Fig.8 Parameter optimization of the machine learning model 对舱段结构同时施加弯矩、轴压和剪力载荷,将相应载荷作用下测点的应力响应数据导入该模型,预测载荷大小。识别载荷与实际施加外载的对比结果如图9所示,其横坐标是归一化后的预测载荷,纵坐标是归一化后的实际载荷,数据点基本都在过原点斜率为1的直线上,证明识别载荷对实际载荷的拟合一致性好,载荷识别效果良好。 图9 真实截面载荷和预测载荷对比Fig.9 Comparison of real section load and predicted load 随着截面载荷增大,结构发生失效破坏的风险越高,表3是在弯矩超过40 kN·m、轴压和剪力超过40 kN的大载荷工况下,模型逆向识别载荷与真实载荷的均方根误差、平均相对误差和最大相对误差。在轴弯剪同时作用下,模型分别对2个正交方向的弯矩M1、M2,剪力载荷Q1、Q2以及轴压T预测的平均相对误差均不超过3%,其中最大相对误差发生在轴压T的识别,此时实际轴压为37.37 kN,预测轴压为42.50 kN,相对误差为12.06%。 表3 机器学习载荷识别误差Table 3 Maximum error of load identification 舱段结构所承受的轴弯剪载荷可视为准静态载荷,参考文献[8-9]中的标定方法,选取典型的测点,标定从载荷到测点响应的传递系数矩阵,逆向求解载荷。加载试验中,沿环向布置的测点对横向剪切载荷不敏感,逆向识别的效果差,因此仅对弯矩M1、M2和轴压T进行计算。标定载荷与应力响应的传递关系以及逆向计算关系如下: (9) (10) 其中:σ1、σ2为2个正交弯矩方向上相对结构中面对称测点对的应力差值,σ3为应力之和。由于舱段结构为非轴对称结构,2个正交方向的弯矩相互耦合,传递系数矩阵非对角阵。由应力响应逆向识别单独作用的载荷结果如表4所示。由于传递系数矩阵中耦合项数值小,易受噪声干扰,因此识别载荷时产生了较大的误差。 表4 标定法载荷识别误差Table 4 Load identification error of calibration method 在弯矩和轴压同时作用的大载荷工况下,标定法与机器学习法的对比分析如图10所示,标定法识别共同作用多载荷的误差显著更高。标定法是在弯矩或轴压单独作用下标定传递系数矩阵,并基于线性叠加原理识别同时作用的弯矩和轴压载荷。而舱段结构形式复杂,载荷之间相互耦合,因此标定法的平均误差显著高于基于机器学习的载荷识别方法。 图10 机器学习方法与标定法载荷识别误差对比Fig.10 Error comparison of load identification between machine learning method and calibration method 针对当前载荷识别难以适用于航天领域中复杂结构和耦合载荷的难题,提出一种基于机器学习的结构载荷逆向识别方法。 1) 通过生成式对抗网络代理模型方法建立高保真仿真模型,生成大规模、高质量的训练数据。 2) 基于高信息熵优化测点布局,减少的测点数量,降低系统复杂度,提升载荷识别效率。 3) 基于充足的高信息熵仿真数据,训练机器学习模型,实现结构上载荷的逆向识别。 在航天器舱段结构截面载荷识别的案例中,方法识别耦合作用的轴弯剪载荷效果明显优于传统标定传递系数矩阵的方法,在工程实际应用中具有可行性,具备将该技术进一步推向工程化应用的条件。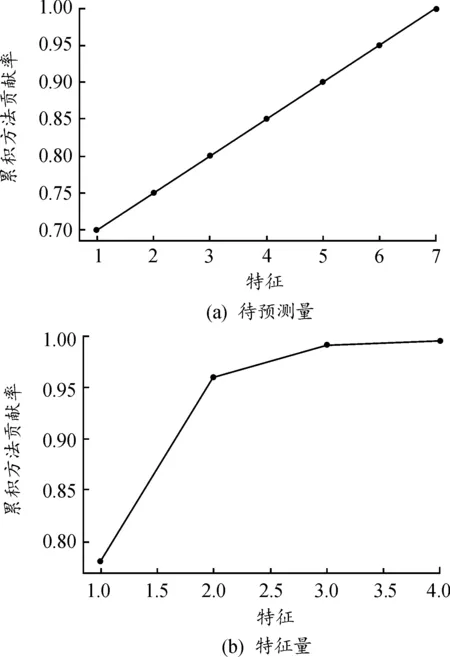

1.3 机器学习载荷识别
2 舱段壳体载荷识别案例
2.1 高保真建模及测点布局优化
2.2 基于机器学习载荷识别
2.3 与标定法的对比分析
3 结论

