基于坐标变换的强间断问题伪弧长算法

陈泽平,王晨涛,李 坤,马天宝

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

0 引言

爆炸与冲击是在高温高压和相变等极端条件下,气液固多介质间强耦合作用的瞬态动力学问题,数值求解该问题模型对航空航天等国防工业及武器装备的研制开发均具有重要的基础应用价值[1-2]。计算爆炸力学很重要的一个问题在于精确捕捉爆轰波的波阵面及波阵面前后物理量的变化,但对于爆炸冲击波的双曲型守恒律方程,其解随着时间的演化往往会出现奇异性即存在强间断,例如激波、接触间断,或者稀疏波之类的弱间断。

为了降低这种奇异性,提高间断分辨率,近年来发展了许多的理论和计算方法,像谱方法、奇异摄动理论、小波分析法[3]以及某些高分辨率的数值格式等。在早期,数值计算捕捉激波通常采取一阶精度的差分格式,后来,Van Leer[4]将一阶Godunov格式进行推广,率先提出了二阶精度MUSCL(monotone upstream-centred schemes for conservation laws),随后近40年,高精度、高分辨率数值格式蓬勃发展,出现诸如TVD、PPM、ENO、RKDG、CE/SE、WENO、WENO-Z及各类杂交格式等。高精度数值格式一般色散较强,容易产生非物理性振荡,通常需要额外的限制振荡的方法,比如人工粘性法,可人工粘性的添加有时会使数值解的耗散比较严重,间断的分辨率不够清晰,其也非从根本上解决振荡。

此外,提升Eulerian法数值求解精度的另一个角度则是网格加密。若采用均匀网格计算求解,便需对整个计算域进行加密,使得计算资源极大地浪费,基于这个矛盾,网格自适应技术应运而生。网格自适应技术大致分三类,h-型(额外增加节点)、p-型(增加逼近多项式的阶数)和r-型(移动网格节点来达到网格重新分布),此外还有正在发展的结合性方法——h-p方法及h-r方法等,这里着重介绍r-型,也即移动网格方法。移动网格法发展至今,其所凭借的网格移动策略及网格泛函逐渐多样化,比如基于变量扩展的等势方法、调和映射、坐标变换的雅可比矩阵思想、基于所谓等分布和对齐条件的泛函等。最近几年,Luo等[5]又将DG(discontinuous galerkin)方法同移动网格偏微分方程法相组合,提出了一种针对双曲守恒律方程的拟拉格朗日移动网格间断Galerkin法,从旧网格到新网格的物理变量并不需要插值;Lopez等[6]还提出一种基于MMPDE法的并行变分网格改进方案。本文中的伪弧长算法可归结为r-型方法。

由于伪弧长算法涉及网格的自适应移动,进而导致原始均匀正交的物理空间发生扭曲变形,这给格式的重构与插值带来了困难。为了避免直接在变形的非结构网格中重构数值格式(需要大量的模板,计算效率较低),根据弧长映射关系,借助坐标变换将物理空间映射至均匀正交的弧长计算空间,然后在弧长计算空间中,基于维数分裂思想可以用较少的模板完成高精格式的重构,从而保证了伪弧长算法的计算效率。伪弧长算法能够将物理空间中的强间断问题转变成均分弧长空间中正常的弱奇异流体问题,而计算空间的转换更保证了原本数值格式的运用,在此过程中还能巧妙地避开虚假振荡。

算法程序的可靠性一直是数值模拟领域亟待解决的重难点,诸如数理模型的简化、边界条件的设置近似以及迭代格式的选取都有可能对计算结果造成偏差[7]。人为解方法(method of manufactured solution,MMS)早期经典工作可现于Oberkampf、Trucano及Roy等。Blais等[8]提出了一种针对VANS方程(the volume-averaged Navier-stokes equations)的人为解方法框架以验证其算法程序,并能同任何CFD技术相结合。Choudhary等[9]介绍了基于旋度而满足无散度约束的人为解方法,以验证两相不可压缩流控制方程。刘学哲等[10]利用其构造的一类二维人为解模型针对性地验证辐射流体力学程序,该办法中动量、能量方程包含源项而质量方程无源项。

本文中研究了二维情况下基于MUSCL的伪弧长算法模型建立过程,针对网格自适应移动造成的物理空间扭曲变形而不易构造高精度格式的难题,基于坐标变换的思想,将变形的物理空间映射至一套正交的弧长计算空间,从而在弧长计算空间中实现控制方程的求解与新网格守恒变量的插值过程,提高了计算效率。编写了该算法相应的一维、二维程序,在人为解方法基础上验证其精度,借助某些经典算例,将PALM数值结果对比分析于有限体积法。

1 伪弧长算法

本节伪弧长算法包含了2个部分。第一部分,借助有限体积法给出物理空间中控制方程的时空离散格式。如前描述,在考虑网格尺度影响的非均匀网格下,格式重构不易,尤其在二维及其以上的情况,因此,第二部分在网格自适应移动之后,采取坐标变换的策略将物理量映射至弧长计算空间中,并在该空间进行格式重构,求解完之后再逆变换映射回原物理空间。

1.1 离散格式

考虑如下双曲守恒系统:

(1)

式中:w为质量、动量、能量组成的守恒变量;F(w),G(w),S(w)为w的函数。

式(1)在网格单元Ki, j上进行积分,得到:

(2)

式中:dσ为面积微元。

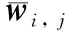
(3)

式中:|Ki, j|为网格Ki, j的面积;∂Ki, j为网格的边界;ds为网格边界长度微元;ni, j为边界∂Ki, j的单位外法向量;δ(w)=(F(w),G(w))。

数值通量借助局部Lax-Friedrichs格式,定义为:

(4)

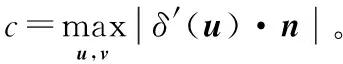
h(u,v,n)=-h(u,v,-n),h(u,u,n)=δ(u)·n

(5)

式(3)写成半离散格式,有:

(6)

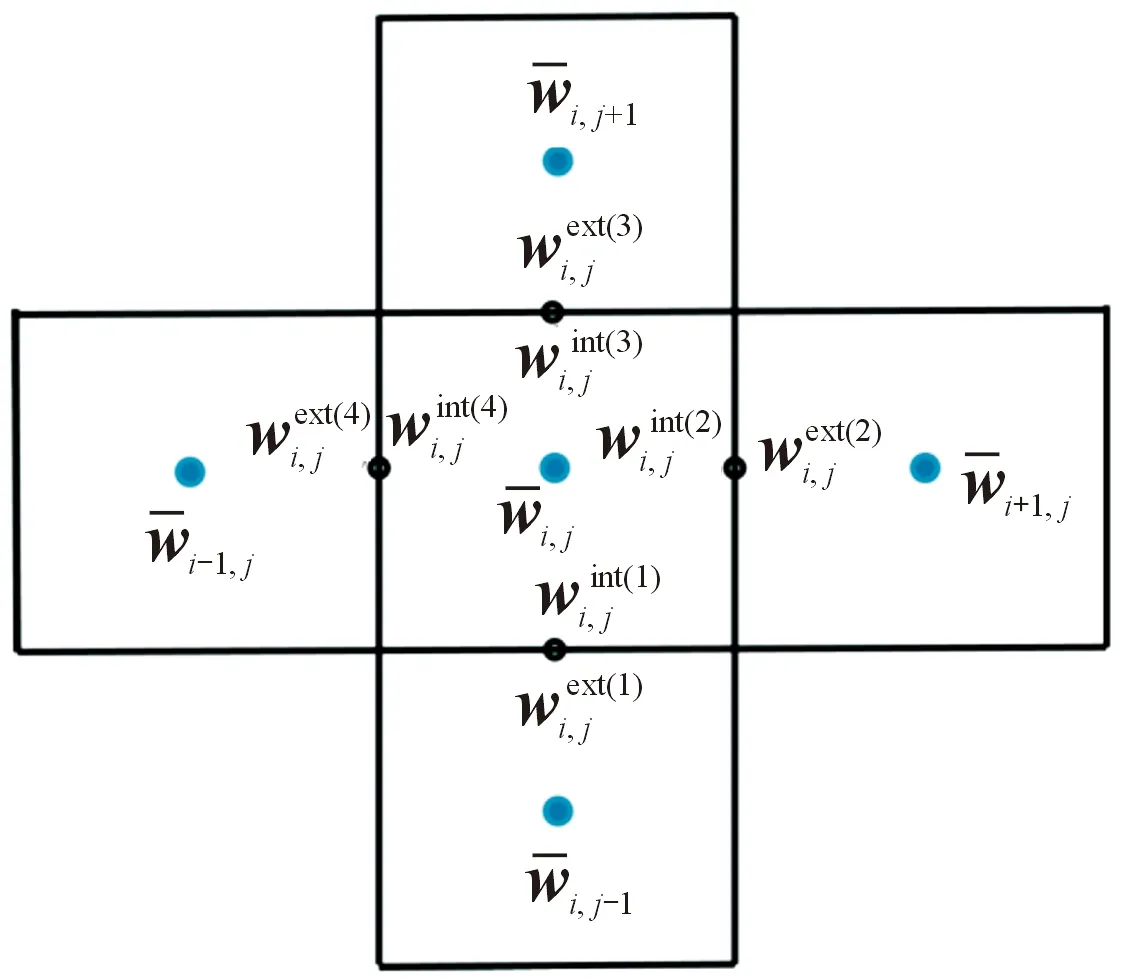
图1 网格单元计算示意图Fig.1 Schematic diagram of grid cell calculation

(7)

式中:ψ为非线性限制器函数。在计算中ψ取[4]:

(8)

式中:ε为小量,可取ε=10-9。

对于时间的离散,忽略掉网格索引i,j,采取如下的三阶TVD-RK格式:

(9)

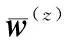
1.2 网格自适应移动与计算空间的转换

以x=(x,y)和ζ=(ξ,η)分别代表物理空间坐标和弧长空间坐标,(xi-1, j-1,xi-1, j,xi, j,xi, j-1)为网格单元Ki, j的4个顶点,从计算空间Ωc到物理空间Ωp的一一对应坐标映射为(x,y)=(x(ξ,η),y(ξ,η))。多维空间要同时照顾到网格的移动速度、方向和尺寸问题,且期望网格朝物理量梯度大之处进行移动,借助变分原理可知,网格的自适应移动将受泛函E(x,y)最小值影响[12]。

(10)

式中:G1,G2为给定的正定对称矩阵;▽=(∂ξ,∂η)T,且有∂ξ=∂/∂ξ,∂η=∂/∂η,则式(10)对应的Euler-Lagrange方程[13]为:

∂ξ(G1∂ξx)+∂η(G1∂ηx)=0

∂ξ(G2∂ξy)+∂η(G2∂ηy)=0

(11)

它对应于泛函临界点。

(12)

具体光滑次数视情况而定,这里不再赘述。令G=wI,如此,进一步简化式(11),有:

▽·(φ▽x)=0

▽·(φ▽y)=0

(13)

对式(13)采用Gauss-Seidel迭代法进行计算,具体步骤如下:

(14)

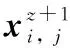
(15)

网格移动完之后,需要得到物理量在新网格上的值,这一步称作物理量重映,本文中采用基于通量的重映方法。如图2二维新旧网格转化图所示。

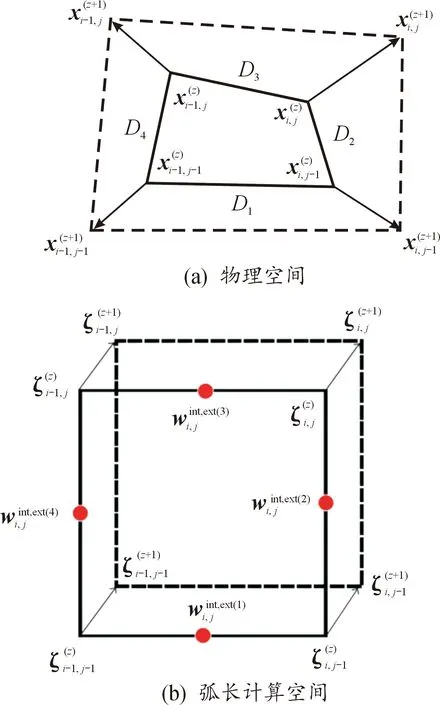
图2 二维新旧网格转换示意图Fig.2 Schematic diagram of old grid transforming to new grid in 2D

设Dk为经过一次迭代物理空间中网格变化导致边∂kKi, j所扫过的面积,则有:

(16)

基于前人的工作[14],考虑到新网格x[k+1]与旧网格x[k]之间通量守恒,得到如下守恒插值格式:

(17)

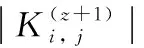
Fk(m,n)=max{Dk,0}·n+min{Dk,0}·m

(18)

引入弧长坐标空间变换式(1)原始双曲守恒方程,得到:

(19)

式中:τ=t,U=ξt+uξx+vξy和V=ηt+uηx+vηy为弧长空间的逆变速度,ψ=w/J,J为空间转换的Jacobian行列式,它的表达式为:

xξyη-xηyξ

(20)

式中:xξ,xη,yη,yξ,xτ,yτ为度量系数,其中,xτ和yτ为网格的移动速度,表达式见式(15)。Jacobian矩阵J的计算可借助几何守恒条件来进行,若能给出J的初值,J的推进便可采取式(21)来计算:

(21)

xξ的计算过程如式(22),其余3个度量系数的计算相类似:

(22)

这样通过式(19)求解完物理量之后,再进行逆变换ψ=w/J,便可得到原始空间物理量。

综上所述,可以给出基于二阶MUSCL的伪弧长算法具体步骤:

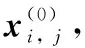
第2步:求解弧长监控函数φ,并根据式(12)进行光滑滤波打磨。

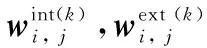
第5步:控制方程的时间步迭代更新,通过式(19)、式(21)及式(22)得到弧长计算坐标系中的控制方程,通过式(9)更新下一时刻物理量,求解完之后再根据逆变换将物理量映射回原物理空间。

第6步:若求解达到终点时间,程序终止,否则转到第3步。

2 精度验证

出于方程跟问题的复杂性,精确解很难获取,因此,这里采用人为解方法对一维、二维程序进行验证。

2.1 一维情况

第1章的理论基于二维情况,对一维而言需降维处理计算,这里不再赘述。针对一维情况构造一组人为解(算例中物理量为无量纲,下同),计算域取[0,2π],计算终止时间tend=2.0,初值条件为:

ρ(x,0)=1.0+0.2sin(x)

u(x,0)=1.0,p(x,0)=1.0

(23)

计算采用周期性边界条件,则其精确解如下:

ρ(x,t)=1.0+0.2sin(x-t)

u(x,t)=1.0,p(x,t)=1.0

(24)

伪弧长控制函数取(a1,a2)=(10,20.25),对于一维、二维情况范数误差公式及收敛阶计算式如下[15]:

(25)

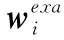
验证结果如表1所示。可以看出伪弧长算法并没有因网格变形而损失太多的精度,随着计算网格数量的增多,其L1误差在逐渐减小,计算结果逐渐接近于精确解,并且,基于MUSCL的伪弧长算法收敛阶也为二阶。将伪弧长算法的误差和收敛阶同有限体积法的进行比较,能看到相同网格数目下,PALM的L1误差一般比固定网格的要小。

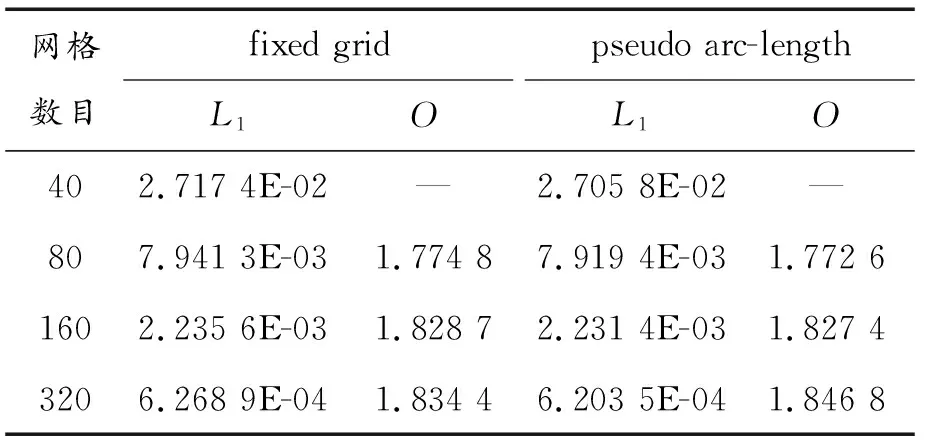
表1 有限体积法与伪弧长算法在不同网格数时的误差和精度(1D)Table 1 Error and accuracy of FVM and PALM(1D)

2.2 二维情况

基于两步化学反应流模型,针对式(1)的双曲守恒系统,令:

(26)

式中:ωα,ωβ为化学反应变化速率,且有:

(27)

式中:α,β分别代表未活化的物质占所有物质的比例和放热反应进行的程度;Q为热释放率;R为气体常数;kα,kβ为反应率常数;Eα,Eβ为激活能。

状态方程:

(28)

式中:γ为比热比。计算域取[0,2π]×[0,2π],计算终止时间tend=2π,给定初值条件:

ρ(x,0)=1.0+0.5sin(x+y)

u(x,0)=v(x,0)=1.0,p(x,0)=1.0

α(x,0)=0.5+0.5sin(x+y)

β(x,0)=0.5+0.5sin(x+y)

(29)

计算采用周期性边界条件,其精确解如下:

ρ(x,t)=1.0+0.5sin(x+y-t)

u(x,t)=v(x,t)=1.0,p(x,t)=1.0

α(x,t)=0.5+0.5sin(x+y-t)

β(x,0)=0.5+0.5sin(x+y-t)

(30)

伪弧长控制函数取(a1,a2)=(6,16)。

验证结果如表2所示。二维情况下伪弧长算法比之固定网格方法同样能适当提高计算精度并减小L1误差。须知,PALM并未增加网格节点,它是根据物理量的分布状况致使网格自适应移动变形,从而在物理量梯度大的地方集聚了较多网格,减小了总体均值误差。随着网格单元数量增多,PALM的L1误差在逐渐减小,且其收敛速度较快,收敛阶更接近于2。

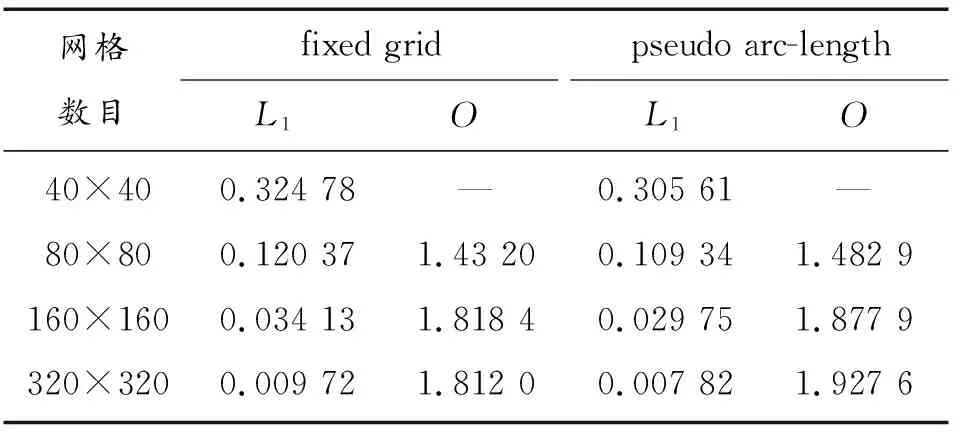
表2 有限体积法与伪弧长算法在不同网格数时的误差和精度(2D)Table 2 Error and accuracy of FVM and PALM(2D)

3 数值算例

下面基于伪弧长算法开展算例验证。

3.1 Sod激波管问题

初值条件:

(31)

计算域为[-5,5],计算终止时间tmax=2.0,边界条件为自由输出边界条件,γ取1.4,伪弧长控制函数为(a1,a2)=(1.7,200),网格数N=150。计算结果如图3所示,分别以Palm、Fixed来代表伪弧长算法和固定网格下有限体积法的数值标识。

该算例参照解(Reference)在5 000个固定网格下获得。对比有限体积法,伪弧长算法能以较少的网格数获得更好的界面分辨率,在相同分辨率的要求下,PALM显得更加高效;同时也发现,要想提高计算精度,相当数目的网格量是必须的。图3(b)给出了移动网格轨迹线图,表征伪弧长算法很好地实现了对奇异间断处的自适应捕捉,在弧长参数作用下,网格点可聚集在激波、接触间断处甚至是稀疏波的头部与尾部。

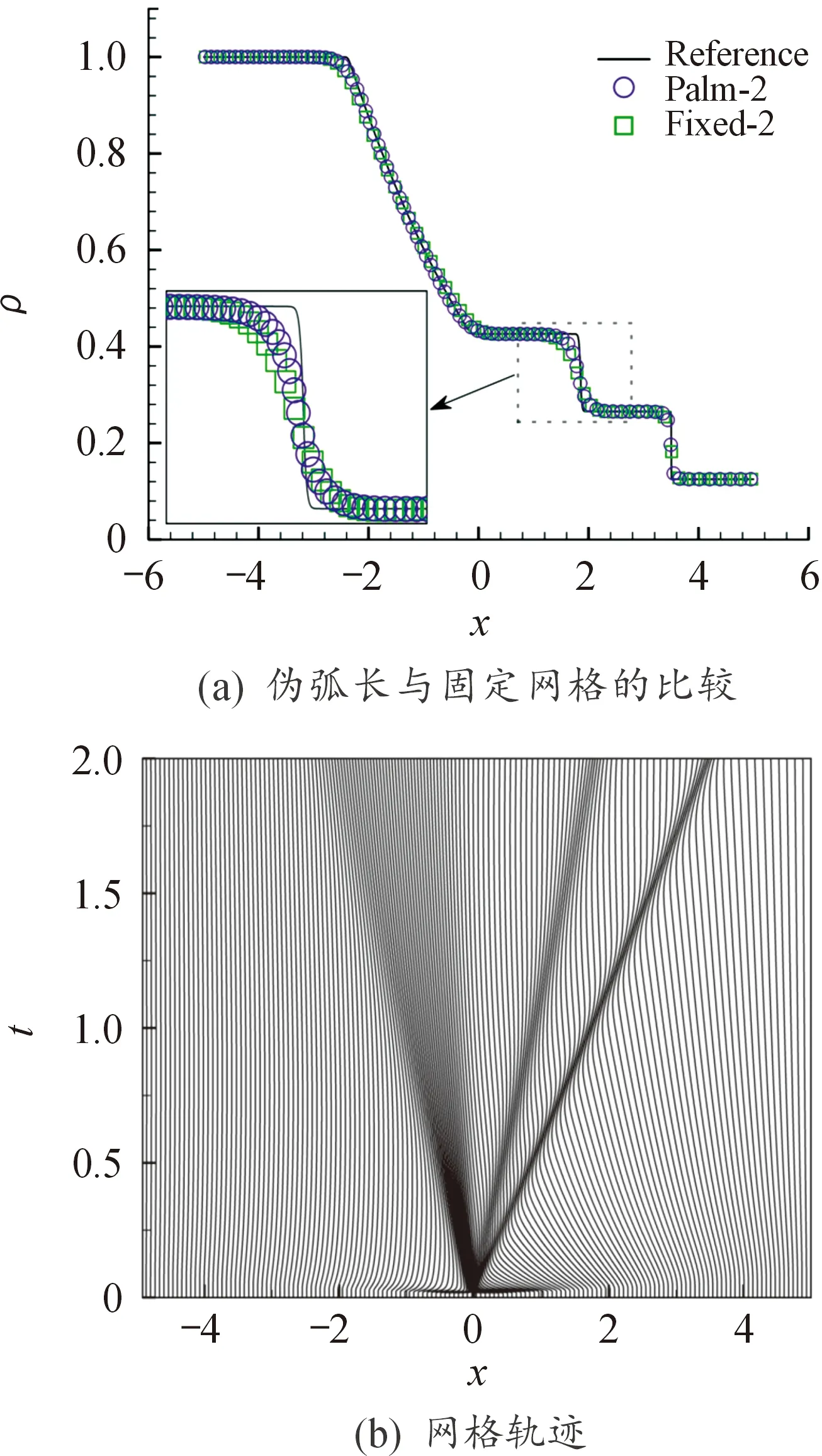
图3 Sod激波管图Fig.3 Results of Sod shock tube

3.2 一维爆炸波

该双爆轰波碰撞问题初值条件如下:

(32)

计算域取[0,1],计算终止时间为tmax=0.038,置CFL系数为0.8,边界条件为反射边界,γ取1.4。计算网格数N=250,伪弧长控制函数以两套不同的参数进行比较,分别为:(2,20)和(2,200),在图4中标识为Palm-2-1和Palm-2-2。由于稀疏波的作用,计算过程中可能会出现负密度、负压力,从而导致程序终止,因此对该算法附加了保正性条件,详细理论见文献[16]。

此算例参照解在10 000个固定网格下获得。图4将3种数值结果同参照解进行比较,说明在网格总数较少情况下伪弧长算法的数值结果显著优于有限体积法,而固定网格算法数值耗散较大,对极值点的捕捉能力很弱。在相同分辨率的要求下,PALM比固定网格法更为高效。图5的网格轨迹线刻画出冲击波在t=0.027时刻左右相撞,之后又沿2个方向继续传播,伪弧长算法对解变化剧烈区域之模拟效果更为逼真。另外能够验证,不同伪弧长监控函数模型对激波的捕捉能力存在差异,针对本算例第二套系数刻画的分辨率的确要优于第一套,其网格移动得更剧烈。

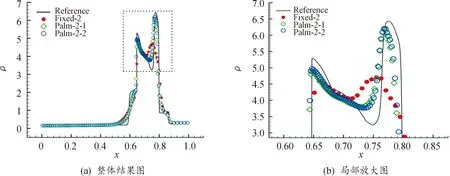
图4 爆炸波问题数值结果比较Fig.4 Numerical results of blast-wave problem

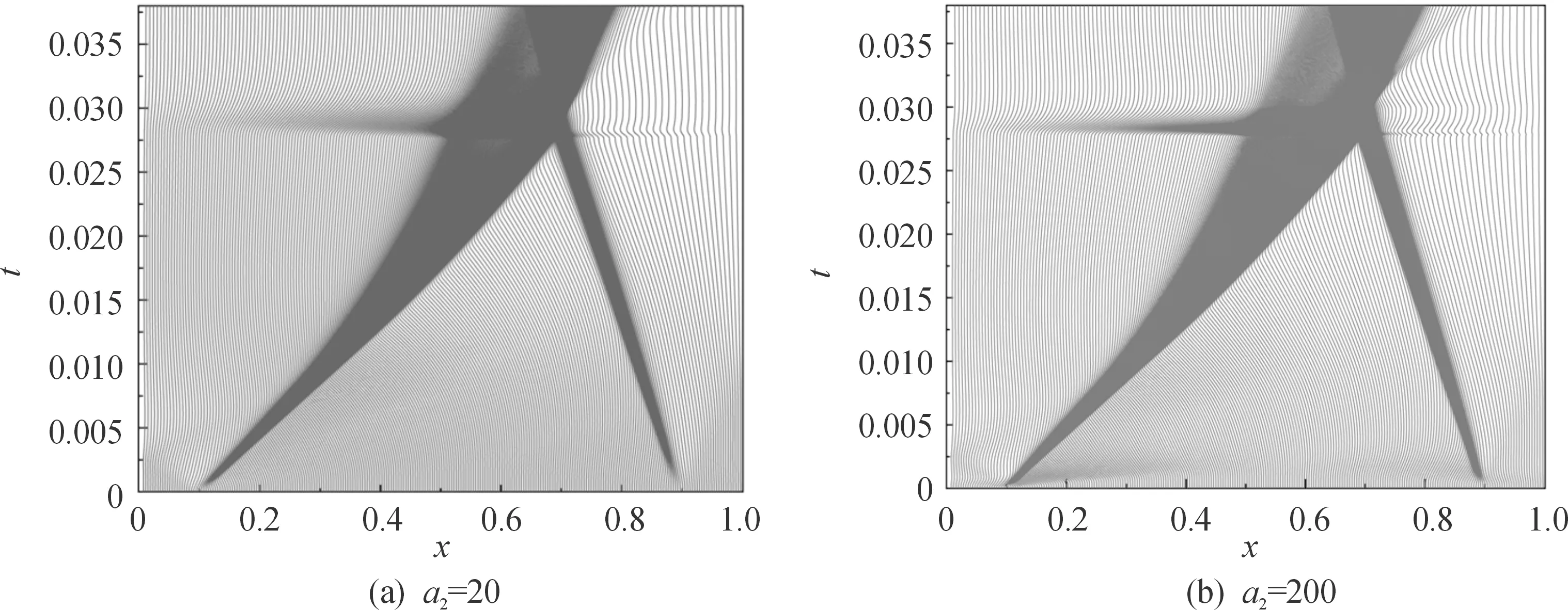
图5 不同参数下网格轨迹图Fig.5 Grid trajectories under different parameters

3.3 二维Riemann问题

在计算域[0,1]×[0,1]内,二维Riemann问题初始分布如图6所示,其边界条件均为流入流出条件。

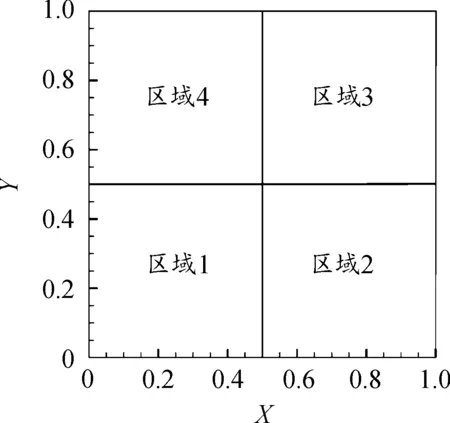
图6 二维Riemann问题初始区域分布图Fig.6 Initial region distribution of two-dimensional Riemann problem

对于这样一个Riemann问题——各有2个正负向滑移线的接触间断,初值条件为:

(33)

计算终止时间为tmax=0.3,伪弧长控制函数取(a1,a2)=(2.7,1 000)。数值结果如图7所示。

图7 二维Riemann问题在t=0.3时刻的密度云图和网格自适应分布图Fig.7 Density cloud map and mesh adaptive distribution map of two-dimensional Riemann problem at t=0.3

借助波传播的形态可以发现,采用200×200的固定网格算法,其模拟的精度较差,密度分布梯度线比较粗糙,而伪弧长算法能更锐利地追踪梯度界面。虽然网格自适应移动会导致额外的局部时间迭代,但移动网格的计算代价比之h-型方法直接加密网格的代价要小,对于求解较大尺度问题,在保证精度的同时,还应减少CPU运行时间,合适的弧长参数下,伪弧长算法的模拟效率要优于固定网格方法。

3.4 双马赫反射问题

该算例是一个波系结构十分复杂的流场问题。为简化模型,将计算域设置在规则区域当中:[0,4]×[0,1]。其中底部(x>1/6为固壁边界,x<1/6为来流)一Mach数为10的斜强激波搁置于x=1/6,y=0处,与x轴成60°角,其他壁面为反射边界条件,模型介绍这里不再赘述。初值条件:

(34)

计算终止时间tmax=0.2,伪弧长控制函数取(a1,a2)=(1,15),该问题在320×80网格数下计算,如图8所示。

图8 双马赫反射问题在t=0.2时刻的密度云图和网格自适应分布图(包含局部细节)Fig.8 Density cloud diagram and grid adaptive distribution diagram (including local details) of dual Mach reflection problem at t=0.2

能够验证二者在流场的大尺度现象(例如跳变点、附壁射流、马赫杆及大致滑移面等)上模拟得相差无几,而图8(b)能更真实地反映流场内波传播的强度与小尺度结构,诸如沿滑移线的小漩涡汇聚现象、第二个三波点等。从局部放大图可以看到,相对固定网格的计算,伪弧长算法对涡核附近以及x=2.5激波相汇区域的计算更为细化。PALM更好地模拟了高马赫数的传播与反射问题。

4 结论

1) 相对于固定网格方法,伪弧长算法在提高爆轰波强间断分辨率上彰显了很好的优越性,本文中基于坐标变换策略发展的弧长算法理论,让爆轰波的求解刻画有效地避开双曲守恒系统的奇异性问题,使得MUSCL格式在弧长计算空间中得到很好地运用,提高了数值求解的分辨率。

2) 对比分析不同伪弧长控制函数对计算精度的影响,验证了监控函数模型的选择将直接影响数值模拟的效果,弧长参数决定网格移动的合理性,网格移动得越剧烈,间断附近的分辨率就越高,但可能会牺牲光滑区域的分辨率且相应增加了迭代步计算。所以采取哪类网格细化准则,构造怎样的伪弧长控制函数(比如多物理量耦合决定、复杂多项式形式等)以及如何选择可调参数,从网格生成这方面来说是一个系统问题,特别在高维空间之时。