对一幅习题插图的纠正及延伸思考

姜兵 邵云

摘   要：从定性分析、实验探究、理论证明、函数作图四个方面，对一道习题的一幅问题插图进行了讨论、纠正，并对大摆角单摆摆线的拉力随时间的变化情况进行了初步的实验探究，发现了一些特点和规律。

关键词：摆线拉力；时间；图像；余弦；摆角

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）4-0057-4

笔者在教学中发现一道习题的插图存在错误，下面通过定性分析、DIS实验探究、理论证明并作图，对该插图进行纠正，同时对相关的内容进行适当的延伸分析。

1    問题的缘起及初步的分析

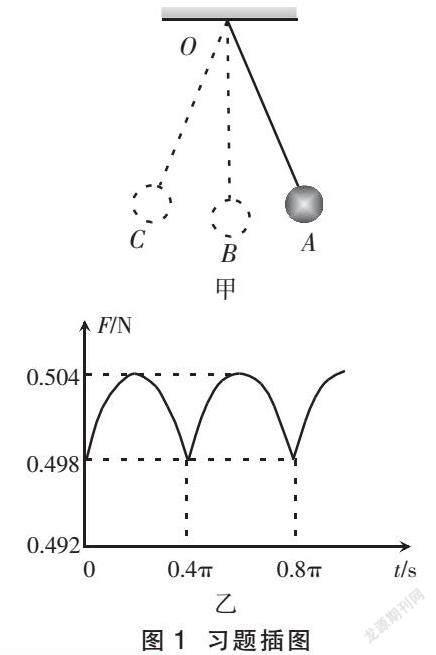
原题 如图1甲所示，O点为单摆的固定悬点，将力传感器接在摆球与O点之间。现将摆球拉到A点，释放摆球，摆球将在竖直平面内A，C两位置之间来回摆动，其中B点为运动中的最低位置。图1乙表示细线对摆球的拉力大小F随时间t的变化曲线，其中t = 0为摆球从A点开始运动的时刻，重力加速度g取10 m/s2。

（1）求单摆的振动周期和摆长；

（2）求摆球的质量；

（3）求摆球运动过程中的最大速度。

这是一道单摆运动规律与力学定律相结合的习题，从题中图1乙所给出的数据信息即可以解出答案。但是，当笔者解完此题后重新审视图1乙时却发现该图并不正确，曲线应该呈现余弦函数曲线的形状，而不是图中的“齿”状。对此分析，提出以下两条理由。

1.1    从因果关系来看

经典物理学中一切连续变化系统内的物理量均应该是连续且可以无限求导的，这是由物质分布与时空分布的连续性及因果律所决定的。要出现图1乙中函数曲线在0.4π s，0.8π s位置其形状上的尖点现象，势必需要巨大的外力（比如冲力）参与才行。显然，图1甲中单摆质点在其最高点A或C并未受到巨大的外力作用，因此图1乙中函数曲线的尖点现象是不应该存在的。

1.2    从最高点瞬时速度等于零的特点来看

摆线拉力最小时摆球位于最高点，此时摆球的瞬时速度为零，并且瞬时速度在该零值附近还“维持”了一小段时间。因此，与速度值相关联的摆线拉力（见下文）也会在此“滞留”一小段时间，即摆线张力在此随时间的变化率（图1乙中曲线的斜率）应该为零。

尽管以上理由看起来已经“十分”充分，但笔者仍然觉得有必要进行更加深入细致的研究。

2    实验探究、理论证明及图像纠正

2.1    利用实验探寻真实的图像

实验器材 上海中将PASCO向心力摆，配套的力传感器，支架，配套的数据传输处理设备。

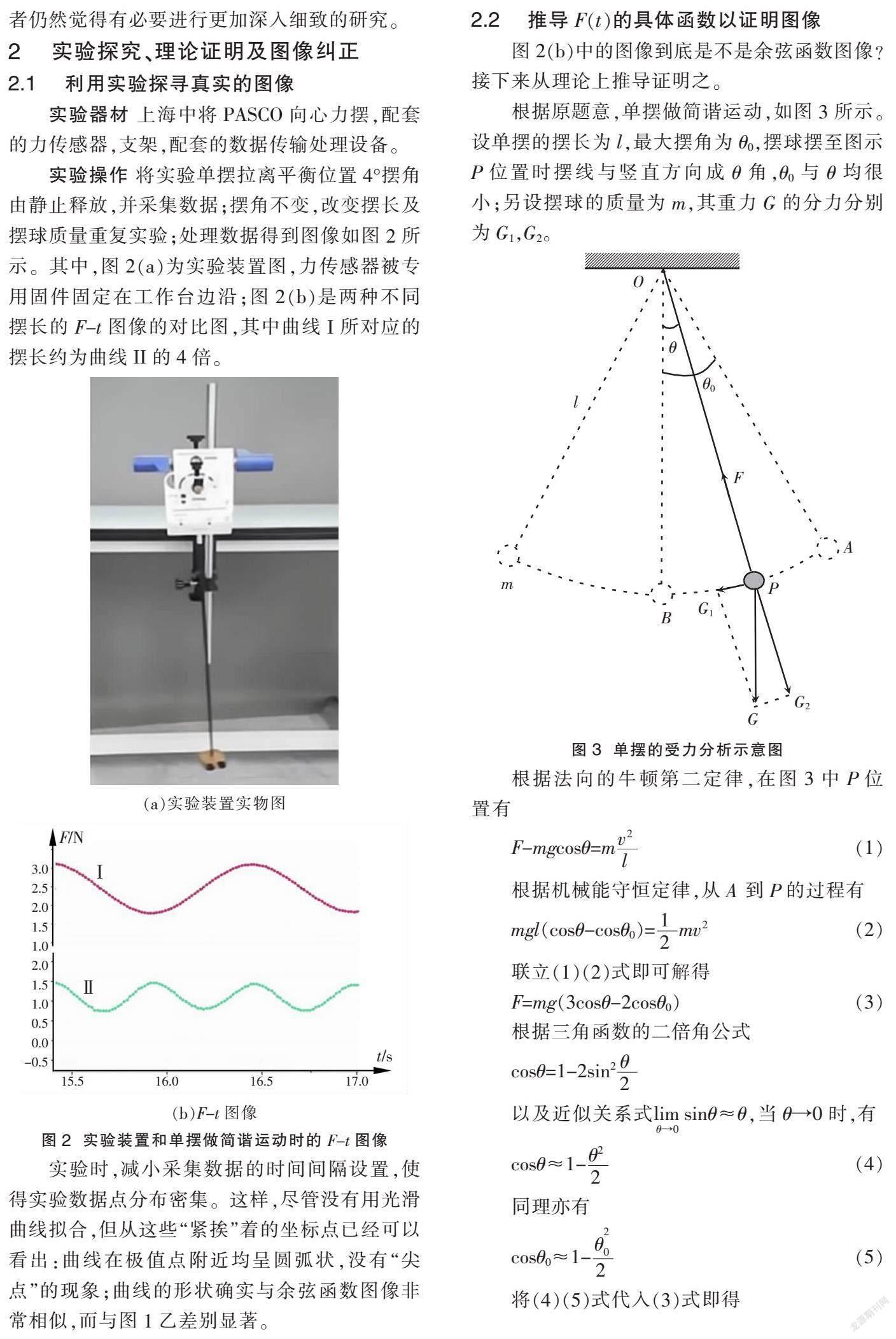
实验操作 将实验单摆拉离平衡位置4°摆角由静止释放，并采集数据；摆角不变，改变摆长及摆球质量重复实验；处理数据得到图像如图2所示。其中，图2（a）为实验装置图，力传感器被专用固件固定在工作台边沿；图2（b）是两种不同摆长的F-t图像的对比图，其中曲线I所对应的摆长约为曲线II的4倍。

实验时，减小采集数据的时间间隔设置，使得实验数据点分布密集。这样，尽管没有用光滑曲线拟合，但从这些“紧挨”着的坐标点已经可以看出：曲线在极值点附近均呈圆弧状，没有“尖点”的现象；曲线的形状确实与余弦函数图像非常相似，而与图1乙差别显著。

2.2    推导F（t）的具体函数以证明图像

图2（b）中的图像到底是不是余弦函数图像？接下来从理论上推导证明之。

根据原题意，单摆做简谐运动，如图3所示。设单摆的摆长为l，最大摆角为θ0，摆球摆至图示P位置时摆线与竖直方向成θ角，θ0与θ均很小；另设摆球的质量为m，其重力G的分力分别为G1，G2。

由（13）式可见，在小角度摆动的情况下，摆线对摆球的拉力近似随时间呈余弦规律变化，这就证明了对图2（b）中曲线形状的余弦猜想。

2.3    对图1乙的纠正

根据F（t）的表达式（13）式并应用Excel软件，即可绘出F-t的正确图像，以纠正原题图1乙。显然，要做到这一点，势必需要根据图1乙中的具体数据，先确定摆长l、摆球质量m、最大摆角θ0的具体数值。其求解过程如下：

3    问题的延伸

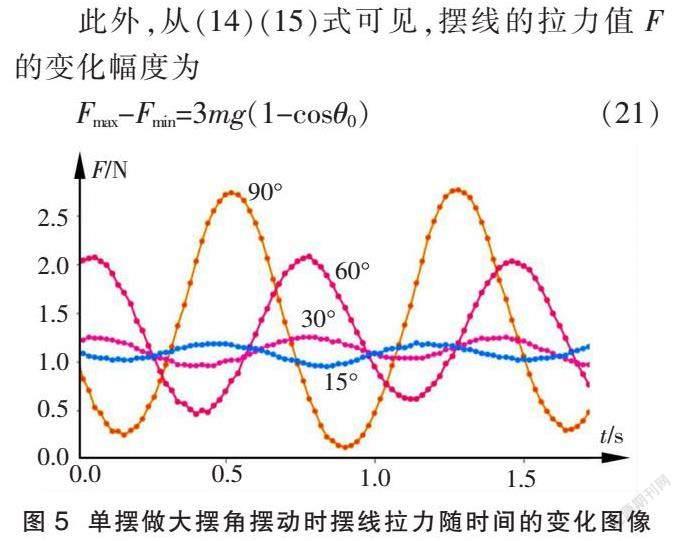
为了进一步了解单摆在大摆角下拉力随时间的变化情况，笔者用一质量为0.108 kg、摆长为0.45 m的单摆，分别做了15°，30°，60°，90°4个大摆角下的摆线拉力监测实验，并绘制出4条相应的拉力随时间的变化曲线，如图5所示。从图5中同一曲线的“波峰”与“波谷”处的等时数据点密度的对比情况大致可见（实验精度原因），摆角越大，“波峰”相对于“波谷”会显得越尖锐，F-t图像会愈加偏离余（正）弦函数图像，愈加表现出“峰细谷粗”的不对称性。

从（21）式不难看出，随着摆角θ0从15°增大至90°，拉力值的变化幅度Fmax-Fmin会越来越大，并且该幅度随摆角θ0增大得也越来越快（cosθ0的缘故），这就解释了图5中15°与30°摆角下拉力幅度Fmax-Fmin变化不大的现象。另外，从图5中又可见，随着摆角θ0的增大，大幅度单摆摆动的周期也在增加。对于该现象的解释，与上文“峰细谷粗”的现象一样，均需要用到较高端的椭圆积分知识。由于这些与本文的主题不甚相关，因此不予讨论，有兴趣的读者不妨尝试加以研究。

4    结  语

本文从定性分析、实验探究、理论证明、函数作图四个方面，对一幅问题插图进行了充分的讨论和纠正。此外，还对大摆角单摆摆线的拉力F随时间t的变化情况进行了初步的实验探究，结果表明：随着摆角θ0的增大，F-t图像会逐渐远离小摆角下的余（正）弦函数图像，逐渐表现出“峰细谷粗”的形状特征。

物理学中一切连续系统内的物理量一般均可以无限地求导，这就相当于数学上的解析函数的概念［1］。这也是判断物理图像是否真实可靠的惯常依据之一。

数字化信息系统实验室（DISLab）设备的使用，可以让我们在不了解物理量的具体函数的情况下，直接获得真实的物理量及其随参量的变化图像。这极大地拓展了我们的物理视野，提升了物理素养。

图像是最简洁、最直观的物理语言之一。尽管图1乙对于原题的求解并不构成直接的影响，但是其不恰当的图像仍可能会对一些读者产生一定的负面影响。因此，图像的制作是习题编制的一个重要的环节，不能随意。

参考文献：

［1］胡嗣柱，倪光炯.数学物理方法（第二版）［M］.北京：高等教育出版社，2002：7-8.

（栏目编辑    蒋小平）