连杆蝶阀运动轨迹分析

黎华 盖晓明 黎勤 田岿

摘 要：连杆蝶阀在很多场合都得到了应用。通过对连杆蝶阀的运动轨迹进行分析，得到了连杆蝶阀各参数之间的关系式和阀板运动轨迹，从而更好的了解阀门的运动特性，对流道进行分析；然后调整各参数，通过求得的关系式进行试算，得到最理想的运动特性。优化设计，以满足各使用场合的要求。

关键词：连杆蝶阀；四连杆机构；运动轨迹；关系式

THE ANALYSIS OF THE MOTION TRAJECTORY OF THE LINKBUTTERFLY VALVE

Li Hua1，2 Gai Xiaoming1，2 Li Qin3 Tian Kui3

（1.Hebei Province Technology Innovation Center of Metallurgical Equipments  Qinhuangdao 066318， China；

2. Qinhuangdao Qinye Heavy Industry Co.， Ltd.  Qinhuangdao  066318，China；

3.Drilling Technology Research Institute of Bohai Drilling Engineering Co.， ltd.  CNPC  Renqiu 062550，China）

Abstract：Link butterfly valve has been applied in many occasions. Through the analysis of the motion trajectory of the link butterfly valve， the relationship between the parameters of the link butterfly valve and the motion trajectory of the valve plate are obtained， so as to better understand the motion characteristics of the valve， analyze the flow channel， and then adjust the parameters. Through the trial calculation of the obtained relationship， the most ideal motion characteristics are obtained， and the design is optimized to meet the requirements of various applications.

Key words：Link Butterfly Valve; Four Bar Linkage; Motion Trajectory; Relation

0 前 言

随着冶炼技术的不断发展，冶金阀门的性能也在不断提高。连杆蝶阀作为一种切断蝶阀，以结构简单、体积小、自重轻、动作灵活、密封性能好、使用寿命长、阀门成本相对低等优点[1]，在冶金行业被广泛应用于炼铁热风炉系统中，在石化、化工、电力等行业得到应用。

连杆蝶阀属于蝶阀的一种结构形式， 其阀门的关闭主要依靠内置于流道的一组四连杆机构的动作来实现。因此，相对于其他蝶阀，其流道内的流动非常复杂[2]，为了对流道进行分析，需要得到阀门的运动轨迹，通过阀门运动轨迹方程，可以合理选择设计参数，优化阀门结构。

1 结构特点和工作原理

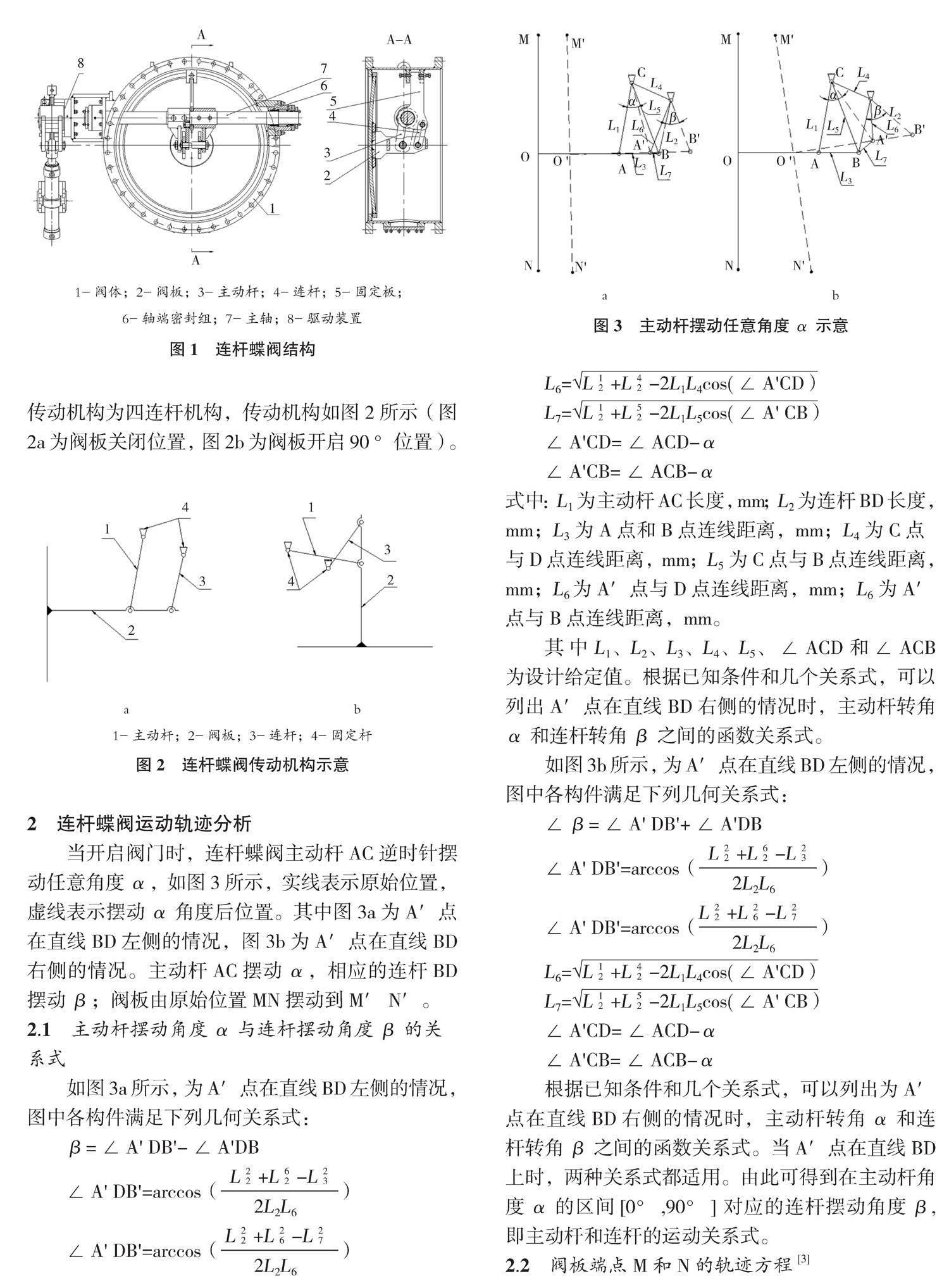
连杆蝶阀的结构如图1所示，其主要由阀体、杆系（阀板、主动杆、连板、固定板）、轴端密封组、主轴、驱动装置等部件组成。

阀门通过驱动装置所输出的扭矩使主轴带动主动杆旋转90 °完成阀门的启闭。其中阀板近似平动+翻转或翻转+近似平动完成90 °旋转过程是由四连杆机构控制的。阀门开启到位时阀板与管道中心线平行；关闭到位时阀板与阀体的密封面平行接触直至压紧密封面，达到阀门的密封要求，其传动机构为四连杆机构，传动机构如图2所示（图2a为阀板关闭位置，图2b为阀板开启90 °位置）。

2 连杆蝶阀运动轨迹分析

当开启阀门时，连杆蝶阀主动杆AC逆时针摆动任意角度α，如图3所示，实线表示原始位置，虚线表示摆动α角度后位置。其中图3a为A′点在直线BD左侧的情况，图3b为A′点在直线BD右侧的情况。主动杆AC摆动α，相应的连杆BD摆动β；阀板由原始位置MN摆动到M′N′。

2.1 主动杆摆动角度α与连杆摆动角度β的关系式

如图3a所示，为A′点在直线BD左侧的情况，图中各构件满足下列几何关系式：

β=∠A' DB'-∠A'DB

L2 2+L6 2-L2 3

∠A' DB'=arccos（——————）

2L2L6

L2 2+L2 6-L2 7

∠A' DB'=arccos（——————）

2L2L6

L6=√L1 2+L4 2-2L1L4cos（∠A'CD）

L7=√L1 2+L5 2-2L1L5cos（∠A' CB）

∠A'CD=∠ACD-α

∠A'CB=∠ACB-α

式中：L1为主动杆AC长度，mm；L2为连杆BD长度，mm；L3为A点和B点连线距离，mm；L4 为C点与D点连线距离，mm；L5 为C点与B点连线距离，mm；L6 为A′点与D点连线距离，mm；L6 为A′点与B点连线距离，mm。

其中L1、L2、L3、L4、L5、∠ACD和∠ACB为设计给定值。根据已知条件和几个关系式，可以列出A′点在直线BD右侧的情况时，主动杆转角α和连杆转角β之间的函数关系式。

如图3b所示，为A′点在直线BD左侧的情况，图中各构件满足下列几何关系式：

∠β=∠A' DB'+∠A'DB

L2 2+L6 2-L2 3

∠A' DB'=arccos（——————）

2L2L6

L2 2+L2 6-L2 7

∠A' DB'=arccos（——————）

2L2L6

L6=√L1 2+L4 2-2L1L4cos（∠A'CD）

L7=√L1 2+L5 2-2L1L5cos（∠A' CB）

∠A'CD=∠ACD-α

∠A'CB=∠ACB-α

根据已知条件和几个关系式，可以列出为A′点在直线BD右侧的情况时，主动杆转角α和连杆转角β之间的函数关系式。当A′点在直线BD上时，两种关系式都适用。由此可得到在主动杆角度α的区间[0°，90°] 对应的连杆摆动角度β，即主动杆和连杆的运动关系式。

2.2 阀板端点M和N的轨迹方程[3]

如图4所示，点M和N为阀板两个端点，以阀板中心为原点O，建立如图所示直角坐标系，并作CE垂直AB于E点、DF垂直AB于F点。图中虚线是当主动杆转过α角时各构件位置示意，各点在坐标系中的坐标记作A（XA，0），B（XB，0），E（XE，0），F（XF，0），A′（XA′，YA′），B′（XB′，YB′）， M′（XM′，YM′）， N′（XN′，YN′）。

由图4中几何关系可点知A′（XA′，YA′），B′（XB′，YB′）坐标如下：

XA'=XE+L1sin（α-∠ACE）

YA' =L8-L1cos（α-∠ACE）

XB'=XF+L2sin（β-∠BDF）

YB'=L9-L2cos（β-∠BDF）

式中：L8 为C点和E点连线距离，mm；L9为D点与F点连线距离，mm。

根据点A′和B′可列出直线A′B′方程式，如下：

y-YA'         x-XA'

———＝————

YB'-YA'           XB' -XA'

即：

YB'-YA'         （XA' （YB' -YA' ）

y= ————x- —————— +YA'

XB' -XA'             XB' -XA'

由直线A′B′方程式可知，直线A′B′的斜率K=YB'-YA'/XB' -XA' ，设直线A′B′与x轴夹角为γ，则γ=tan-1 （YB' -YA' ）/（XB'-XA' ）。已知直线M′N′与直线A′B′垂直，则直线M′N′与y轴夹角为λ=90°-|tan-1XA'-XB'/YB' -YA'  |

上述各式中L8、L9、XE、XF、和∠ACE、∠BDF为设计给定值，并且上节已得到α和β的关系式，因此γ也可由α表示出来。

如图5所示，过M′点作直线a，过N′点作直线b，过点A′作直线A′T，上述各直线均与x轴平行；然后过A′点分别向直线a和直线b作垂线，垂足分别是P、Q，则可得到如下方程两个参数方程：

XM' =XA' -L10cos（∠M' A' O'-γ）

YM' =YA' +L10sin（∠M' A' O'-γ）             （1）

XN' =XA' -L11cos（∠M' A' O'-γ）

YN' =YA' +L11sin（∠M' A' O'-γ）             （2）

上面方程中，L10 、L11 、∠M' A' O'和∠N' A' O'为设计给定值，且由已知条件知∠M' A' O'和∠N' A' O'相等，并且XA'、YA'、γ均可由α表示，因此XM′， YM′为变量α的函数，方程（1）为点M′（XM′，YM′）中XM′，YM所在曲线的参数方程；XN′，Y N′为变量α的函数，方程（2）为点N′（X N′，YN′）中X N′，YN′所在曲线的参数方程。根据这两个参数方程，就可画出阀板端点M和N的运动轨迹曲线。

3 应用实例

为了更直观的表示各函数之间的关系，这里以DN1400连杆蝶阀为例，绘制各函数曲线。DN1400连杆蝶阀各参数如下：

L1=254、L2=193、L3=140、L4=150

L5=267.4、L8=250、L9=188.4、

L10=L11=708.7、XE=327.5、

XF=464.5、∠ACD=76°、∠ACB=31°、

∠ACE=10.2°、∠BDF=12.56°、

∠M' A' O'=∠N' A' O'=66.5 °

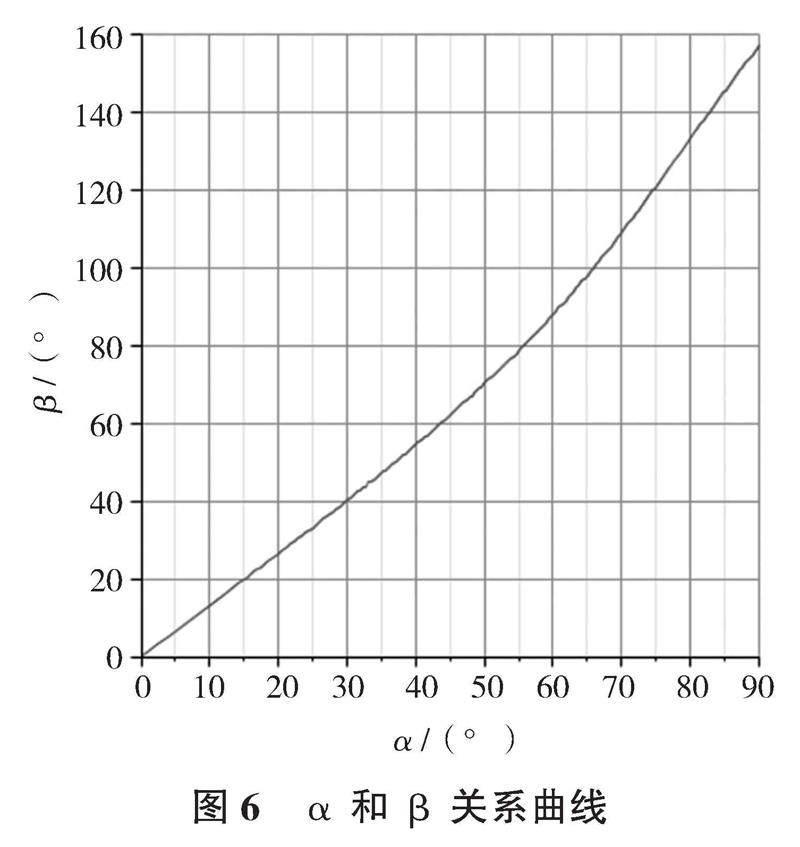
根据求得的各关系式，利用Maple14软件得到α与β关系曲线。

从图6可知，β随着α的增大而增大， 并且β变化速度比α快。

图7所示为α与阀板所在直线M′N′与y轴夹角λ关系曲线，其中图7a为阀板从关闭到完全开启整个过程中α与λ关系曲线，图7b为α在[0°-20°]变化区间α与λ关系曲线。

从图7a中可以看出，阀板所在直线M′N′与y轴夹角λ总的变化趋势为随α的增大而增大。从图7b中进一步分析可知，在阀板开启初期，即α由0°变化到14.5°过程中，阀板所在直线M′N′与y轴夹角λ先增大后减小；在初始位置和主动杆转过角度α为14.5°时，λ值均为0°。

从图8、图9可以看出，当M点横坐标XM在区间[0，105]变化，对应N点横坐标XN变化区间[0，200]时，（从参数方程可解出此时对应α变化区间为[0°，35.3°]），阀板近似平动，之后转动。

4 结束语

连杆蝶阀具有开关速度快，制造成本低，开启位置准确和占用空间小等特点[4]，连杆蝶阀的这些特点使之在很多场合都得到了很好的应用。通过对连杆蝶阀的运动轨迹进行分析，得到了连杆蝶阀各参数之间的关系式和阀板运动轨迹，从而更好的了解阀门的运动特性，对流道进行分析，然后调整各参数，通过求得的关系式进行试算，得到最理想的运动特性，以满足各使用场合的要求。

参考文献

[1] 吴怀敏，苏荆攀，项力胜，等.高温用金属密封蝶阀[J].阀门，2018（2）：44-45.

[2] 邢卫平，崔兵兵，马学东.连杆蝶阀的流场分析[J].机械工程师，2011（7）：71-72.

[3] 徐付霞.三连杆蝶阀阀板运动轨迹的计算[J].阀门，1994（3）：4-8.

[4] 赵文辉.四杆机构蝶阀的设计与应用[J].甘肃农业，2014（2）：65-66.