如何判断-2.00D与-1.00D的大小？

孙鹏锐

眼科临床医生与视光医生对于-2.00D与-1.00D到底应该表述为-2.00D＞-1.00D还是-2.00D＜-1.00D存在分歧。二者到底谁大谁小，值得深入探讨。

近视程度的分类有两种恰好相反的表述方式。其中《眼科学》（第九版）中定义轻度近视≤-3.00D，而《儿童屈光矫正专家共识（2017）》中定义近视≥-3.00D为低度近视，可以看出两者对于近视程度分类标准统一存在差异，即比较符号上不一致。作为眼科临床医生，认可轻度近视≤-3.00D的表述方式。但近年来随着儿童青少年近视防控关注度越来越高，眼视光专业飞速发展，眼视光领域相关内容急剧增多，低度近视为≥-3.00D的定义方式越来越常见。

最初，由于度数可以按照数学的运算方法进行加减，因此笔者按照数学含义理解“+”“-”，但无法解释-2.00D＞-1.00D的表述；于是笔者又按照光学含义理解“+”“-”，200度高于100度，但又不能解释-2.00D＜-1.00D的表述。经过思考与研究发现，从口头表述看：无论远视还是近视，2.00D都高于1.00D，意思明确不会引起争论。如果用文字来表述远视：+2.00D＜+3.00D，也没有争论，但用文字表述近视时，便出现了分歧。笔者认为，只要统一近视中“-”的含义，便可达成共识。

从定义角度看，屈光指来自外界的光线在光学系统界面发生偏折（可以是会聚，也可以是发散）时的现象；屈光力指光线在界面偏折的程度，屈光度（D）是屈光力的单位，大小用离开光线交汇点的距离（单位：m）的倒数来表达。

光学中，光线通过屈光系统后如果会聚，用“+”表示，如果发散，用“-”表示；矫正远视眼用凸透镜，凸透镜会聚光线，所以验光单中出现“+”就是远视；同理，矫正近视眼用凹透镜，凹透镜发散光线，验光单中出现“-”即近视。“+”“-”后面的数字大小表示镜片会聚或发散光线能力的强弱。比如+2.00D、+1.00D两个镜片，前者会聚光线的能力强于后者，度数高；-2.00D、-1.00D两个镜片，前者发散光线的能力强于后者，度数高。按照这种理解，图1屈光度轴从0度开始向左近视度数越来越大，向右远视度数越来越大，方向相反，所以-2.00D＞-1.00D。

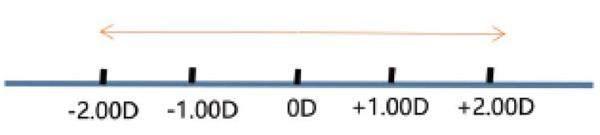
图1 屈光度轴

但视光医生们认为，在定量语境中，近视应始终被视为一个负值，数学比较符号应严格按数学意义使用。在实际使用过程中，就会出现图2数轴的情况，无论近视数值还是远视数值，从左至右只有一个方向，所以-2.00D＜-1.00D。

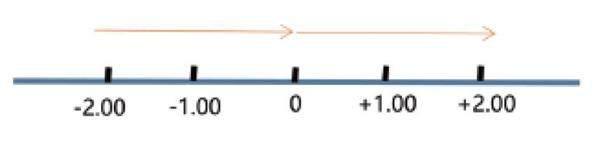
图2 数轴

无论图1屈光度轴还是图2数轴，远视数值都是从左至右越来越大，如果近视数值从左至右也是越来越大，那么远视数值和近视数值的方向就可以统一起来。图2本身就是这个方向，不存在问题，但图1中方向相反，如何让-2.00D＜-1.00D成立？需转换思路，当镜片发散能力强时，它的会聚能力必然弱，-2.00D会聚光线的能力弱于-1.00D，由此-1.00D＞-2.00D在光学中也成立。无论按光学还是数学解释，这个比较式都可以解释。

图3

但矫正近视用的凹透镜是发散光线，为什么要比较会聚能力？验光中如果遇到近视-2.00D、-1.00D和远视+1.00D、+2.00D的结果，都会优先选择-1.00D和+2.00D。图3可见选取度数的原则为选取两个度数之中在轴右侧的度数。这与前面说的方向重合，从左至右不仅数值越来越大，会聚能力也越来越大。之所以选取其中会聚能力大的镜片，是因为会聚可以放松调节，选取会聚能力最大的镜片可以保证眼睛放松调节最大，是验光追求的目标，即视光学中所说的MPMVA（maximum plus to maximum visual acuity）原则。

尽管在实际工作中MPMVA（maximum plus to maximum visual acuity）原则被从业者所熟知，但不同书籍或文章对其翻译却不尽相同（为保证准确，配有截图）：

翻译1：MPMVA=最正球镜时的最佳视力（见图4a、图4b）

图4a 刘家琦，李凤鸣.实用眼科学（第3版）.北京：人民卫生出版社，2010，550页.

图4b  陈辉，管怀进.眼视光学.2013，53页.

翻译2：MPMVA=最正之最佳视力（见图5）

图5 瞿佳.眼视光学理论和方法（第3版）.北京：人民卫生出版社，2018，80页.

翻译3：MPMVA=最高的正屈光度获得最佳视力（见图6）

图6 杨培增，范先群.眼科学（第9版）.北京：人民卫生出版社，2018，228页.

翻译4：MPMVA=最大正镜最佳视力（见图7）

图7 陈玲，温龙波，蓝卫忠，等.3～12岁儿童静态屈光度的估算模型.中华眼视光学与视觉科学杂志，2020，22（1）：60.DOI：10.3760/cma.j.issn.1674-845X.2020.01.010.

在实际验光应用中，使用的原则都相同，但是对英文意思理解的不同，造成各类文献中对其翻译也不同。哪一种翻译准确，如何理解才是最好的呢？

英文语境中，对maximum visual acuity的理解是一致的，均翻译为：“最佳视力”，to：prep.到、向、往（某方向或某处）、位于……方向、到达（某处）。此处可翻译为到、之、至，个人认为“至”似乎更合适一些。差异主要是对maximum plus的理解不一致，maximum：adj.最高的、最多的、最大极限的；plus：n.优势、好处、长处、加号；其中对plus的理解是关键，加号（+），即正，我们知道实际应用中对应的还有minus：n. 减号、负号、负值、缺点；意为负号（-），即负。正（+）、负（-）符号在眼视光中其实包含两层含义：第一层含义在光学中表示的是光线偏折以后是会聚还是发散状态，会聚用“+”表示，发散用“-”表示；第二层含义在数学上表示的是正值和负值。光学是一门高度数学化的科学，任何定量描述符号都必须在数学上有效，最符合逻辑的方法是将近视视为负值，远视视为正值，严格遵循其数学意义。

在验光过程中，当不能使用睫状肌麻痹药物时，一般会使用雾视法来替代，雾视就是在眼前加一定屈光度的正镜片，以到达一定的视力后再验光，其目的是为了去除过度的调节痉挛，放松眼睛。因为正镜片可以减少调节，负镜片可以增加调节，正视的定义是在眼调节放松状态时，外界的平行光线经眼的屈光系统后恰好在视网膜黄斑中心凹处聚集。这一提法在远视验光原则中没有问题，当+1.00D和+2.00D都可以矫正至最佳视力时，为了足矫，会选择+2.00D，即选择最大正镜或最高的正屈光度。这解释了为什么MPMVA原则翻译当中会出现正球镜、正屈光度这样的说法。英文原文中并没有出现spherical（球镜）、diopter（屈光度）的单词，所以翻译时也不应出现相关的内容。但在近视验光时，MPMVA原则中并没有提到如何选择负（-），在应用中，选择的标准会描述为选择最小的负度数最佳视力（图8），也就是说，近视-2.00D和-1.00D都可以矫正到最佳视力时，选择-1.00D。

图8（截自某公众号）

按照上面的度数选择原则，理论上除了MPMVA原则，还应该存在MMMVA（minimum minus to maximum visual acuity）原则：最小负之最佳视力。但实际上，视光中只有MPMVA原则存在，这是因为MPMVA原则已经包括了远视及近视的度数选择原则，这也是为什么plus只能翻译为“正”，不能翻译为正镜片的原因，“正”的含义表示的是会聚的能力，包含正负两种镜片，两种镜片都可以认为是有“会聚”能力的，无论哪种镜片，度数选择的原则都是选取两个度数之中在轴右侧的度数，符合最正的含义。

由此，图5中的翻译应该是最准确的，MPMVA：最正之最佳视力。个人认为翻译为“最正至最佳视力”更合适。这种翻译把光学和数学的含义都包含在内，把正负镜片都包含在内是极简且恰当的表达，可以解决眼科临床医生和视光医生之间的争辩。行业内应该统一认识，认可并推广近视≥-3.00D为低度近视的这种表述方式。

作者单位：西安医学院第一附属医院眼科