基于关联规则学生成绩预警研究

杨令叶?黄学茂

摘要：高校学生成绩预警是高校教务管理的重要工作之一，研究高校学生学业预警问题在理论层面和实践指导层面均具有重要的价值。采用关联规则算法中的Apriori算法来分析厦门工学院2016级至2018级学生的成绩数据，探究每个专业各课程之间的关联度。在Matlab环境下用Apriori算法对信息与计算科学专业的学生学业成绩进行挖掘分析，发现该专业下不同课程间的关联关系，尤其是对先修课程与后继课程间的关联规则的挖掘，及时对挂科的学生预警，并同时给任课教师提供指导，从而提高教育教学管理水平。

关键词：关联规则；学业预警；Apriori算法

一、Apriori算法介绍

Apriori算法本质是属于逐层查找迭代算法的一种形式。借助候选项集生成频繁项集，挖掘出布尔型关联规则，并计算出相应的支持度、置信度，此两个标准用来表示关联规则的强度。其基本思想是利用频繁项集的先验知识以递归的方法判断候选集是否为频繁项集并且找出最大频繁项集，利用频繁项集生成仅包含其非空子集的关联规则。

二、算法的流程及分析

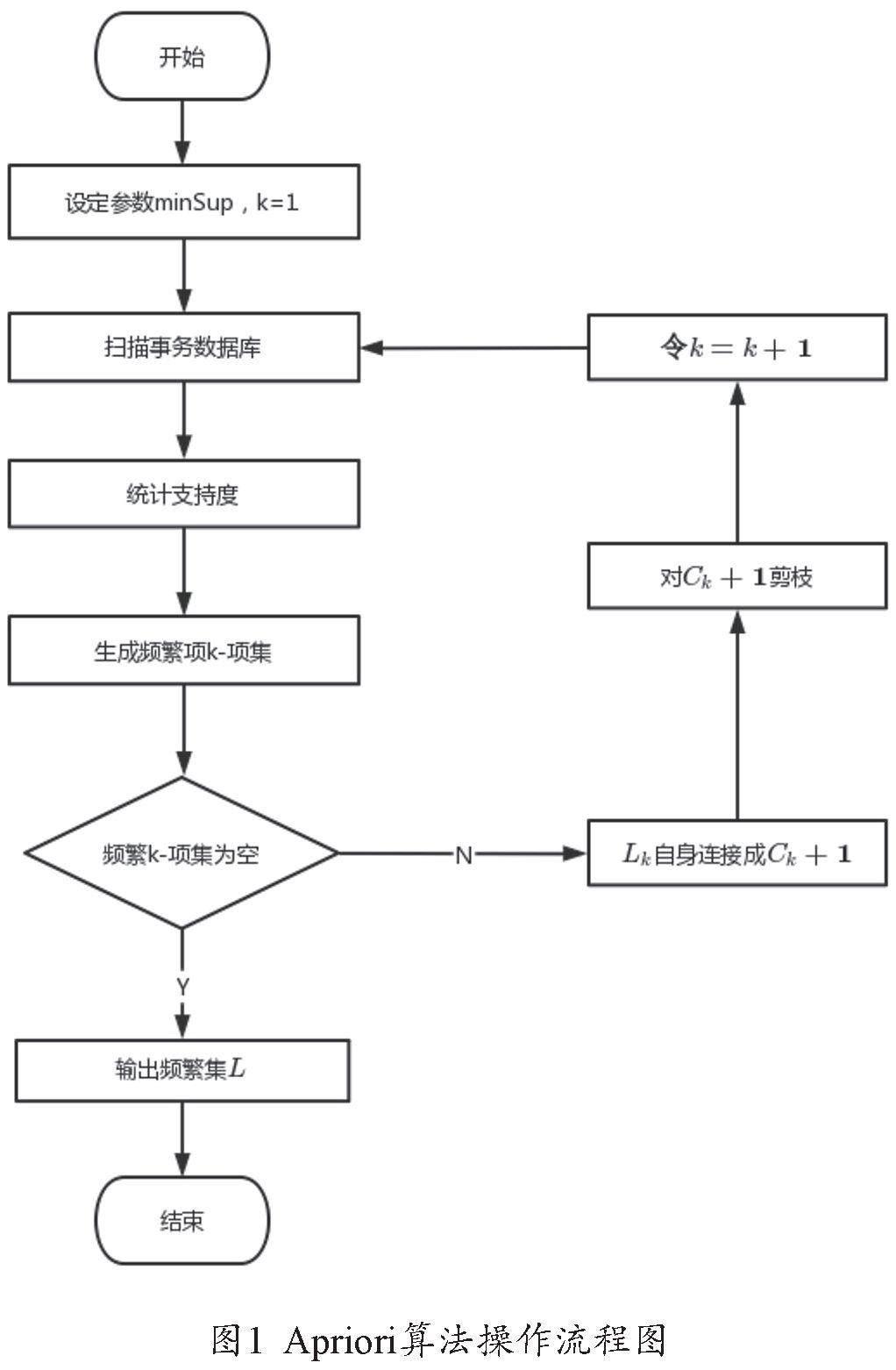
Apriori算法是利用k-项集来生成（k+1）－项集迭代的方法，其操作流程如图1所示，设定最小支持度minSup、最小置信度minConf。第一步，扫描学业成绩数据库，保留满足最小支持度的候选项1-项，得到频繁集1-项集L1；第二步，由L1自身相连生成2-项C2，将得到的C2进行剪枝操作，统计2-项集的项数，删除不满足minSup的项集，得到频繁项集2-项集L2；进行多次迭代，找到满足条件的最大频繁项集k-项集Lk，最终得到频繁项集：L={L1，L2，L3，...，Lk}

Apriori算法挖掘频繁项集具体的过程如下[1]：

1.连接步骤：Lk-1经过自身连接得到k-项集Ck。如果Lk-1中的某两个元素（集合）ik-1 和ik-2 的前（k-2）个项是相同，则称ik-1 和ik-2 是可连接的。所以ik-1 和ik-2 连接产生的结果集是：

i={i1[1]，i1[2]，i1[3]，...，i1[k-1]，i2[k-1]}

2.剪枝：利用任何两个非频繁项集的超集都不是频繁集的性质，如果项集Ck的子集不属于Lk-1，则该子集是非频繁，则从Ck中删除。

3.删除：利用上文中得到的Ck，统计剪枝后的每一项的项数，删除不满足条件的项，最终得到频繁k-项集Lk。

三、数据准备

所使用的原始数据来源于厦门工学院教务系统内2016级至2018级共计9000余名学生的学业成绩数据。为了便于对关联规则进行挖掘分析，选取信息与计算科学专业学生的学业成绩进行挖掘，且在源数据提取时，不考虑补考和重修的成绩，只保留学生正考成绩。

（一）学生学业成绩数据预处理[2]

本次实验的数据来源于厦门工学院教务管理系统数据库，具有规范性和真实性。原始数据进行算法分析时需要生成适用于Apriori算法的布尔型数据，进而实现算法在成绩数据挖掘中的应用。

1.数据消减

针对缺项数据，则需要删除这类学生的异常成绩数据。

2.数据标准化[3]

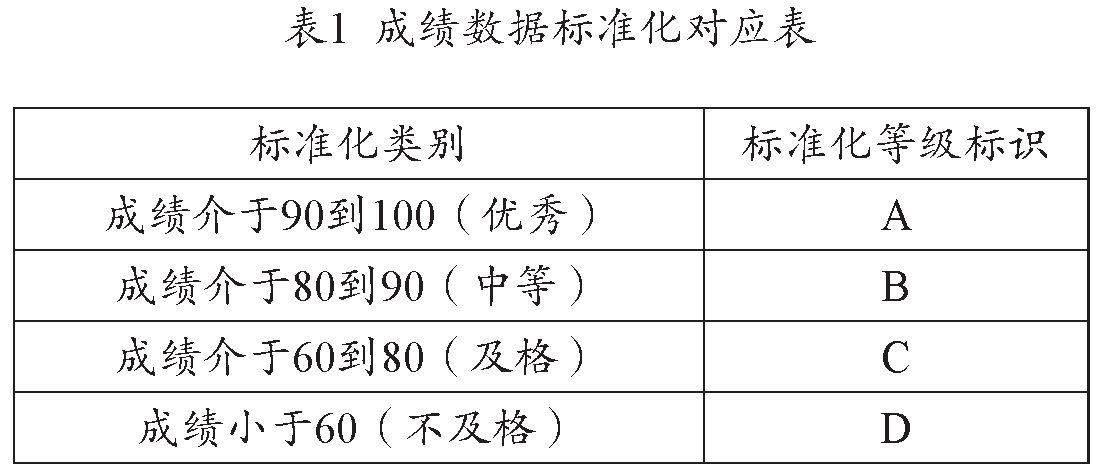
在学生的学业成绩表里，少数课程录入的成绩为四级制（优秀、中等、及格、不及格 ）。为了使成绩数据在挖掘过程中统一规则，需要针对这类数据进行标准化处理。成绩数据标准化对应表如表1所示。对应规则设定完成，再将学生的学业成绩数据基于学号作为主键进行数据转化。

3.成绩数据离散化

按照Apriori算法函数的作用，将标准化后的学生学业成绩进行离散化处理，并且为了简化表格，把表中列出的全部课程成绩按代码来表示，离散化后的数据表如表2所示。

四、关联参数阈值确定

首先通过试探法来确定支持度的最佳值，设定置信度阈值minConf=0.9，试探得出当支持度为0.3时，关联规则分析的结果最具有代表性，因此我们将支持度设置为0.3，并使用Apriori算法来对该数据集进行分析[5]。如表3。

同理通过试探法来确定置信度的最佳值，根据上一步实验得到的最优支持度minSup=0.3，试探得出当置信度minConf=0.8时，关联规则分析的结果最具有代表性，由此可得最优置信度设置为0.8，如表4。

由表4可得，最优的关联规则阈值为：{支持度minSup=0.3，置信度minConf=0.8}。

五、关联规则结果

在 Matlab2018a 环境下，运用 Apriori 算法对预处理的成绩数据进行挖掘，采用上文确定的最优支持度和置信度{minSup=0.3，minConf=0.8}，挖掘出不同的关联规则。在分析的过程中，我们得到了一个包含了各种课程成绩频繁项集的列表，其中支持度和置信度都达到了预设的阈值。将强关联规则以列表的形式呈现出来，在本文中，挖掘出的关联规则，如表5所示。

六、实验结果分析

本次实验共挖掘出27个频繁项集，其中包含了该专业学生的各个成绩属性组合情况。在27个频繁项集中，选取其中支持度、置信度较高的一些关联规则进行分析，根据表中列出的关联规则可知：

（一）规则12，该专业学生在｛高等代数（一）C，高等代数（二）C｝课程中都取得了中等（C）的成绩，那么该学生在｛复变函数C｝课程中也很可能取得中等（C）的成绩，支持度70.48%、置信度为80.76%，支持度越大，说明在该专业的学生中该三门课程同时取得中等（C）的成绩非常普遍，且前置课程的成绩对后置课程的成绩的影响比较大，影响的概率为80.76%。

（二）规则5：｛数据结构D -> 数据库原理D｝，该规则的支持度为50.24%、置信度为81.75%，则表明该专业的学生成绩系统中显示有一门｛数据结构｝不及格（D），根据关联规则得出他需要注意｛数据库原理｝课程的学习，同时需要加强｛数据结构｝课程的指导及复习。

（三）从规则 10、13、16、27 中可以看到，数学类相关课程的成绩与程序语言类，以及专业课的成绩存在一定关联性，其原因是数学类课程是计算机编程逻辑的基础课程，数学类课程对于学生逻辑思维能力的提升具有不可替代的作用。而语言类编程课程的学习一般都是基于逻辑思维来学习的，所以若是数学类的课程成绩较差，后续的语言类课程也会学不好或者出现不及格的现象。

综上所述，通过本次实验可以看出，关联规则挖掘技术可以对学生学业成绩之间的关系进行发掘和分析，从而为学生的学习提供有益的指导和帮助，促进学生成长和发展[4]。

参考文献

[1]王吉.教务数据的分析与预测——以建宁七中为例.北京：清华大学出版社，2018：25-28.

[2]吴蓓.基于决策树算法的成绩预测模型研究及应用[M].北京：人民邮电出版社，2019：13-16.

[3]都娟，翟社平.基于改进 Apriori 算法的高校学生成绩预警系统的研究[M]．北京：人民邮电出版社，2018：108-109.

[4]胡金涛.基于C4.5决策树的学生成绩预测教学系统的研究与实现[D].西安：西南交通大学，2017．

[5]毋雪雁，王水花，张煜东.K最近邻算法理论与应用综述[J].计算机工程与应用，2017，53（21）：1-7.