基于密度泛函理论和含时密度泛函理论下 富勒烯B24N24光谱性质研究

郭雅晶 库雁兵 李秀燕

摘 要    ：本文在B3LYP/6-31g（d）基组水平上，利用密度泛函理论（DFT）优化了B  24N  24团簇的几何和电子结构. 研究结果表明，优化所得B  24N  24团簇的几何结构对称性分别为S  4、C  2、S  8和O；在基态稳定结构基础上，得出其输运性质，既非p型输运材料，亦非n型输运材料，即不具有输运性质；在优化好的基态结构基础上，又研究了它的红外和拉曼分子振动谱，四种团簇的红外-拉曼振动谱的振动强度排序均为O>S  8>S  4>C  2；随后采用含时密度泛函理论（TDDFT），同样在B3LYP/6-31g（d）基组水平上，计算了这四种物质在CH  2Cl  2溶剂中的UV-Vis吸收谱特性，研究表明跃迁能级数量越多，吸收谱振动强度越强，并且这些分子的紫外-可见吸收谱的振动强度排序为S  4>C  2>S  8>O.

关键词 ：含时密度泛函理论； 红外； 拉曼； 密度泛函理论

中图分类号 ： O561 文献标识码 ：A DOI ：  10.19907/j.0490-6756.2023.045002

收稿日期：  2023-02-24

基金项目：  国家自然科学基金（11804246）；山西省科技厅基础研究计划面上项目（202203021221214）

作者简介：   郭雅晶（1986-）， 女， 山西太原人， 硕士， 高级实验师， 主要研究方向为凝聚态物理新型低维材料.  E-mail： guoyajing58@163.com

DFT and TDDFT study on spectra of B  24N  24 fullerene

GUO Ya-Jing  1， KU Yan-Bing  2， LI Xiu-Yan  3

（1. Department of Physics， Taiyuan Normal University， Jinzhong 030619， China;

2. Shanxi Road and Bridge Construct Co.， LTD.， Lüliang 033000， China;

3. College of Physics and Optoelectronics， Taiyuan University of Technology， Taiyuan 030024， China）

The geometrical and electronic structure of B  24N  24 are optimized by using density functional theory （B3LYP） at the 6-31g（d） level. The results show that the geometrical structure symmetries of the optimized B  24N  24 clusters are S  4， C  2， S  8， O. Based on the stable structure of the ground state， it is concluded that its transport properties are neither the p-type transport material， nor the n-type transport material， so， they have no transport properties. On the basis of the optimized ground state structure， the IR-Raman spectra of the four clusters were obtained. And the order of vibrational intensity for the IR-Raman spectra of the four clusters is O>S  8>S  4>C  2. The Time-Dependent Density Functional Theory （TDDFT） was also used at the B3LYP/6 -31 g （d） level， the UV-Vis absorption spectra of these four compounds in CH  2Cl  2 were calculated， the results show that the more transition energy levels， the stronger the vibration intensity of the absorption spectrum. The vibrational intensities of the UV-Vis absorption spectra of these molecules are sorted as S  4>C  2>S  8>O.

Time-dependent density functional theory; Infrared; Raman; Density functional theory

1 引 言

由于富勒烯及相关类富勒烯纳米笼形结构具有潜在的电学、光学和磁学应用价值，人们对该类物质进行了深入研究  ［1］. Radowan等  ［2］对富勒烯团簇及其衍生物进行了研究.这引起了人们对（BN）   n 类富勒烯结构特殊性质继续研究的兴趣. 与富勒烯C   n 相比，（BN）   n 具有良好的物理稳定性和化学惰性  ［3］. 作为富勒烯C   n 的等电子类似物，带隙能约为6 eV，且具有高能带、低温超导性、抗氧化性和较高的热力学稳定性等独特的物理化学性质  ［4］. 除此以外，Stephan等人  ［5］在纳米材料的电子辐射下合成了单层及嵌套的（BN）   n （ n =12， 16， 28）物质；Oku 等人  ［6］通过电弧熔融法和激光质谱法合成并检测了B  24N  24团簇. 同富勒烯C   n 对比，氮化硼属于杂化富勒烯，它在构型方面遵循孤立四边形法则（ISR）  ［7］. 在笼形结构的（BN）   n （ n >10）中，孤立四边形法则是指结构中的六个四元环完全被六元环分离，此时该物质具有相对较低能量且结构稳定  ［8］. 通过理论计算，Wu等人  ［9］研究发现，遵循孤立四边形法则的氮化硼团簇比对应的含有五边形和六边形的（BN）   n 具有较高的稳定性. 该结论与Strout  ［10］和Stephan等人  ［5］的研究结果一致.

Wu等人  ［9］还根据密度泛函理论研究计算发现最稳定的B  24N  24类富勒烯结构的点群为S  8. 它由两个八边形、十六个六边形和八个四边形键合而成. 该团簇的结构稳定性高于仅由四元环和六元环构成的B  24N  24. 为了进一步研究B  24N  24团簇稳定结构的基态和激发态光谱性质，本文使用密度泛函理论（DFT）和含时密度泛函理论（TDDFT）量子化学计算方法，选取了富勒烯B  24N  24团簇的多种同分异构体为对比研究对象，通过TDDFT对大分子团簇在溶剂效应下进行计算，建立了适用于富勒烯（BN）   n 的紫外可见吸收光谱，为较大体系笼形结构物质的光谱研究提供参考与借鉴.

2 计算细节

所有富勒烯结构采用Gaussian 09软件包  ［11］在B3LYP/6-31g（d）基组水平  ［12］上运用密度泛函理论（DFT）进行优化. 在考虑了不同的自旋多重性和大量的初始结构，还运用相同基组水平分析了振动频率，重点研究了B  24N  24四种稳定富勒烯结构  ［13］. 在相同的理论水平上进行了谐波振动频率分析，并找出势能面上最小值，并且这里考虑的所有分子虚频值均为零（NIMAG=0）  ［14］. 基态分子的几何结构图像和分子轨道（MO）图像通过GaussView5.0  ［15］程序生成.

为了进一步分析B  24N  24同分异构体的内部输运特征，在其基态结构的基础上，分别仿真计算了它们的电离势（ IP ）、电子亲和势（ EA ）、空穴/电子提取势（ HEP/EEP ）和空穴/电子重组能（ λ   h/ λ   e，eV）. 与此同时，在这些团簇稳定结构的基础上，还分别研究了它们的红外（IR）和拉曼（Raman）振动波谱，通过振动谱来分析它们的内部结构特征. 除此之外，还采用含时密度泛函理论（TD-DFT）结合极化连续介质模型（PCM）中的自洽反应场（SCRF）在CH  2Cl  2溶剂中来计算这四个同分异构体的紫外-可见吸收光谱（UV-Vis）.

3 结果和讨论

3.1 几何结构

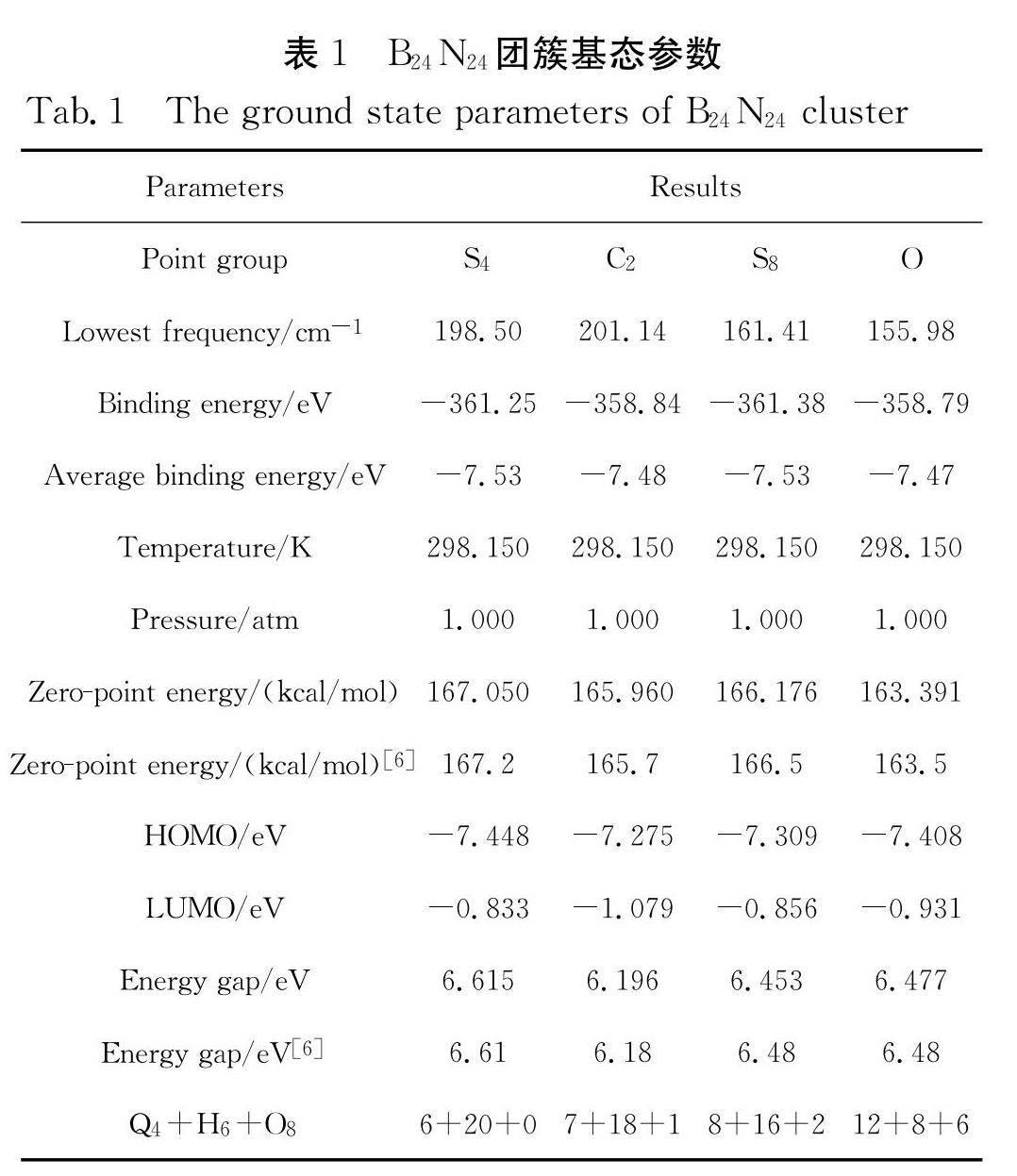
通过GaussView5.0构建了富勒烯B  24N  24多种点群结构，结合Gaussian 09程序在B3LYP/6-31g（d）基组水平上运用密度泛函理论（DFT）进行优化，并取得如图1所示四种稳定的基态结构. 从图1可以看出，粉色原子为硼原子（B），蓝色原子为氮原子（N），每个原子符号前的数字为设置分子结构时原子排列顺序数，且右下标S  4、C  2、S  8、O分别为各同分异构体的对称性（在下文中将分别用S  4、C  2、S  8、O代表四种团簇，用来区分这些同分异构体）. 这四种结构分别由四边形、六边形和八边形键合而成. 考虑到孤立四边形法则，结合八边形参与其中构型的稳定性便会出现图1中的多种对称性稳定结构. 将图1与表1对照，表1中将四边形数量用Q  4表示，六边形的数量用H  6表示，八边形的数量则用O  8表示. 此外，表1还给出了这些同分异构体的基态对称性、最低频率、结合能、平均结合能、温度、压力、零点能、最高占据能HOMO、最低未被占据能LUMO和能隙.

从表1中得出，四种同分异构体最低频率均大于0 cm  -1，则说明在该基组水平下计算所得最低频率都为正值，位于势能面的局部最小值，即NIMAG为0（无虚频）. 再者，文献［6］的实验所得值与本文理论计算值对比可见，计算所得零点能167.050、165.960、166.176和163.391 eV与实验值167.2、165.7、166.5和163.5 eV非常接近，存在偏差是由于实验环境相较理论计算环境而言，总会存在外部细微干扰或不可抗因素. 表中的能隙值，实验所得为6.61、6.18、6.48和6.48 eV和计算值6.615、6.196、6.453和6.477 eV非常吻合，这进一步说明文中所选取优化基组水平是合理的. 对比表1中的四种同分异构体的结合能和平均结合能发现，拥有八个四边形、十六个六边形和两个八边形的对称性为S  8的B  24N  24最稳定，其次是具有六个四边形、二十个六边形对称性为S  4的B  24N  24团簇，排在最后的是具有十二个四边形、八个六边形、六个八边形对称性为O的B  24N  24分子，对称性为C  2的同分异构体B  24N  24分子则趋于S  4和O之间. 由此结果表明，对称性为S  8的B  24N  24最稳定，四种分子的稳定性排序为S  8>S  4>C  2>O.这与Wu等人  ［9］的研究结果是一致的.

3.2 重组能

图2列出了富勒烯B  24N  24分子四种同分异构体的前线分子轨道，图中横坐标下的S  4、C  2、S  8、O分别为对应分子的对称性，纵坐标为HOMO、LUMO轨道所对应能级. 从图2中可看出，四中团簇的HOMO轨道主要执行π键轨道而LUMO轨道主要执行π *反键轨道，与此同时HOMO和LUMO能级π轨道特征以及离域的程度均在所有异构体的原子核. 所有异构体的HOMO轨道由N原子的p轨道形成p-π共轭，而B原子的p轨道几乎没有贡献；LUMO轨道由B原子的p轨道形成有效的p-π *共轭，而N原子的p轨道几乎没有贡献.

表2给出了这四种同分异构体的电离势（ IP ，eV）、电子亲和能（ EA ，eV）、空穴/电子提取势（ HEP / EEP ，eV）和空穴/电子重组能量（ λ   h/ λ   e，eV）. 结合表1和表2可看出，共轭键的电离势和电子亲和能的变化与HOMO和LUMO能级的变化一致，如表1中B  24N  24同分异构体的HOMO能级大小顺序为S  4>O>S  8>C  2，并伴随有电离势随其顺序反向增加；而同分异构体的LUMO能级大小顺序为C  2>O>S  8>S  4，电子亲和能亦随其顺序反向增加. 由此可见，载流子的传输与前线分子轨道的分布密切相关，一般来讲，p型输运材料的 IP  A在5.680～6.786 eV范围内，n型输运材料 EA  A在2.411～3.141 eV范围内， IP  A和 EA  A材料的双极性传递应在5.905～7.026 eV和2.797～3.479 eV范围内. 由上述结果讨论可得出，B  24N  24的四类同分异构体既非p型输运材料、亦非n型输运材料，也不具有双极性传递性质.

3.3 红外和拉曼振动谱

在优化基态结构的基础上，在相同基组水平（B3LYP/6-31g（d））下分别计算了这四种同分异构体的红外和拉曼振动谱. 图3给出了富勒烯 B  24N  24同分异构体的红外和拉曼光谱，对称性为S  4的 B  24N  24团簇对应黑色光谱，对称性为C  2的B  24N  24团簇对应红色光谱，对称性为S  8的B  24N  24团簇对应绿色光谱，对称性为O的B  24N  24团簇对应橙色光谱.

从红外光谱可以看出，这四种分子的振动频率主要集中在750～900 cm  -1和1350～1550 cm  -1之间，900～1350 cm  -1中间有少数零星散发的振动峰，振动强度弱；这四种同分异构体的振动最强峰均在1500 cm  -1处，四个团簇相比，对称性为O的B  24N  24在该出的振动峰最强，其次是对应绿色波谱的S  8，然后是对应黑色波谱的S  4，最后是对应红色波谱的C  2. 由图3中的拉曼波谱看出，各分子的拉曼振动峰遍布100～1600 cm  -1之间，比各自相对应的红外振动波峰数量多；所有分子的两个最强拉曼振动峰集中在400～500 cm  -1和800～900 cm  -1之间，并且橙色振动谱对称性为O的B  24N  24在这两处的振动强度最大，其次是对应绿色波谱的S  8，然后是对应黑色波谱的S  4，最后是对应红色波谱的C  2.这与红外振动谱的研究结果相同.

由上述研究得出，红外吸收光谱的波数在500～ 1600 cm  -1之间，属于中红外区（400～4000 cm  -1，2.5～25 μm），即属于基本振动区；这四种团簇的红外光谱振动强度排序为O>S  8>S  4>C  2. 对于拉曼光谱，这四种同分异构体的振动强度排序亦为O>S  8>S  4>C  2. 由于这四种团簇的构型为非线性分子，故这些分子的振动自由度为3 n -6个（ n 为原子数）.

3.4 紫外-可见吸收谱

运用含时密度泛函理论（TDDFT），结合极化连续介质模型（PCM）中的自洽反应场（SCRF）在原有基组水平（B3LYP/6-31g（d））上计算了四种同分异构体溶于CH  2Cl  2溶剂的紫外可见吸收谱（UV-Vis）. 图4给出了四中团簇在CH  2Cl  2溶剂中的吸收谱，点群为S  4的B  24N  24对应黑色吸收谱，点群为C  2的B  24N  24对应红色吸收谱，点群为S  8的B  24N  24对应绿色吸收谱，点群为O的B  24N  24对应橙色吸收谱. 表3给出了所有分子在CH  2Cl  2溶剂中的吸收特性，同时列出了部分主要能级跃迁和占比百分以及对应波长和振动强度；表中列出了相应峰值的能量跃迁出处，例如图4中S  4在202.30 nm最高吸收峰吸收能量主要是由于HOMO-5→LUMO  （36%）、HOMO-2→LUMO+1（10%）和HOMO→LUMO+4（22.4%）的轨道电子跃迁产生.

由图4可以看出，B  24N  24分子的吸收峰波长集中在175～270 nm之间，并且都只有一个最强吸收峰，四个团簇相比对称性为S  4的吸收峰振动强度最强，其次是C  2，然后是S  8，最后是O；可见所有团簇的吸收谱波长均在紫外波长范围内（10～400 nm）  ［16］，处于高频短波段UVC（100～280 nm）  ［17］，而且处于灭 菌紫外线（200～280 nm）  ［18］波段和制臭氧紫外线（100～200 nm）  ［19］波段. 结合表3可得，跃迁能级数量越多，吸收谱振动强度越强，例如S  8与O相比，S  8的吸收峰振动强度比O吸收峰强，并且贡献于S  8吸收峰的跃迁能级数量比O的多；同样以S  4和S  8相对比，S  4的吸收峰振动强度之所以比S  8强，是由于作用于S  4吸收峰的跃迁能级数量多于S  8；所有分子的紫外-可见吸收谱的振动强度排序为S  4>C  2>S  8>O.

4 结 论

基于密度泛函理论（DFT）在B3LYP/6-31g（d） 基组水平上，研究了优化后的类富勒烯B  24N  24四种同分异构体的基态性能（点群、结合能、虚频、能隙、重组能和红外-拉曼振动谱等）. 结果表明，四种B  24N  24团簇基态结构对称性分别为S  4（由6个四边形，20个六边形构成）、C  2（由7个四边形，18个六边形，1个八边形构成）、S  8（由8个四边形，16个六边形，2个八边形构成）和O（由12个四边形，8个六边形，16个八边形构成）；B  24N  24的四类同分异构体既非p型输运材料、亦非n型输运材料，也不具有双极性传递性质；四种团簇的红外-拉曼振动谱的振动强度排序均为O>S  8>S  4>C  2. 随后采用含时密度泛函理论（TDDFT）同样在B3LYP/6-31g（d）基组水平上，计算了这四种物质在CH  2Cl  2溶剂中的UV-Vis吸收谱特性，研究表明跃迁能级数量越多，吸收谱振动强度越强；并且这些分子的紫外-可见吸收谱的振动强度排序为S  4>C  2>  S  8>O.

参考文献：

［1］   Wang Y， Yao M G， Hua X，  et al . Structural evolution of D  5h（1）-C  90 under high pressure： A mediate allotrope of nanocarbon from zero-dimensional fullerene to one-dimensional nanotube［J］. Chin Phys Lett， 2022， 39： 056101.

［2］  Radowan A， Elmorsy K， Hassan A H，  et al . Manganese dioxide （MnO  2）/fullerene-C  60-modified electrodes for the voltammetric determination of rifaximin ［J］. J Anal Test， 2021， 5： 341.

［3］  Xie G Y， Lv H， Chen X，  et al . The discovery structure properties and application of fullerene C  60   ［J］. Carbon， 2021， 3： 34.

［4］  Goyal R N， Gupta V K， Bachheti N. Fullerene-C  60-modified electrode as a sensitive voltammetric sensor for detection of nandrolone-an anabolic steroid used in doping ［J］. Anal Chim Acta， 2007， 597： 82.

［5］  Stephan O， Bando Y. Atomic structure and electronic state of boron nitride fullerenes and nanotubes［J］. Appl Phys A， 1998， 67： 107.

［6］  Oku T， Kuno M， Narita I. Structure and stability of perazido substituted azacycloalkanes ［J］. Diamond Relat Mater， 2002， 11： 940.

［7］  Orfanopoulos M， Kambourakis S. Fullerene C  60 and C  70 photosensitized oxygenation of olefins ［J］. Tetrahedron Lett， 2014， 35： 1945.

［8］  Zope R R， Dunlap B I. Are hemispherical caps of boron-nitride nanotubes possible？ ［J］. Chem Phys Lett， 2004， 386： 403.

［9］  Wu H S， Xu X H， Zhang F Q，  et al . What is the most stable B  24N  24 fullerene？ ［J］. J Phys Chem A， 2003， 107： 6609.

［10］  Strout D L. Structure of boron nitride E-phase： diamond lattice of B  12N  12 fullerenes ［J］. Chem Phys Lett， 2004， 95： 383.

［11］ Frisch M J， Trucks G W， Schlegel H B，  et al . Gaussian 09 ［M］. Revision A.02. Wallingford CT： Gaussian Inc.， 2009.

［12］ Frisch A， Nielsen AB， Holder A J. Gaussview user manual ［M］. Pittsburgh PA： Gaussian Inc.， 2005.

［13］ Rassolov V A， Ratner M A， Pople J A，  et al . 6-31G * Basis set for third-row atoms ［J］. J Comput Chem， 2001， 22： 976.

［14］ Rassolov V A， Pople J A， Ratner M A，  et al . 6-31G * basis set for atoms K through Zn ［J］. J Chem Phys， 1998， 109： 1223.

［15］ Frisch A， Nielsen A B， Holder A J. Gaussview 5.0 ［M］. Pittsburgh PA： Gaussian Inc.， 2005.

［16］ Runge E， Gross E K U. Density-functional theory for time-dependent systems ［J］. Phys Rev Lett， 1984， 52： 997.

［17］ Wang J L， Zhou X L， Wang G H，  et al . Optimally stuffed fullerene structures of silicon nanoclusters ［J］. Phys Rev B， 2005， 71： 113412.

［18］ Tian W Q， Chen D L， Cui Y H，  et al . Structures， stabilities， electronic and optical properties of fullerenes （C  50-C  68） and derivatives ［J］. Comput Theor Nanosci， 2009， 6： 239.

［19］ Zope R R， Baruah T， Pederson M R，  et al . Theoretical infrared， Raman， and optical spetra of the B  36N  36 cage ［J］. Phys Rev A， 2005， 71： 025201.