堑尾翼型的表面结构设计及其气动性能的仿真探究

王涵信 卢业玮 肖新愉 李均 孟庆鑫 张宇

关键词 翼型优化;气动性能;流体仿真;翼尾湍流;升阻比

流体力学中连续性方程与伯努利方程是固定翼飞机设计的理论基础，在此基础上的大量实验结果表明，翼型的升力与来流速度、流体密度以及翼型形状均有关[1]。飞行器的不断发展促进了机翼的进一步优化，由于机翼的形状直接影响着飞机的气动特性，因此研究与改良翼型具有重要意义。在20世纪30年代初期，美国国家航空咨询会（缩写为NACA，后改为NASA）对低速翼型进行了系统的实验研究。在1932年，确定了NACA四位数翼型族。不同的翼型具有其独特的几何特性和气动特性，便于设计人员选取理想翼型。在现有翼型资料中，NACA 系列翼型的资料较为丰富，飞行器也较多采用这一系列的翼型。

国内外学者针对不同领域的技术要求相继提出了对已有翼型的各种优化方案，给予了翼型研究新的内容和使命。Chakshu Baweja等[2]以波音737的翼型为模板，发现尾缘凹陷的存在极大地改变了机翼上方的流动分离，有效地延缓了边界层的分离，提升了机翼的气动性。Rabii EL MAANI等[3]采用ANSYS/Fluent软件对NACA0012翼型在不同马赫数下的二维跨音速流动进行了数值模拟，结果与实验吻合，并用遗传算法高效地优化了翼型气动性能。李治国等[4]在叶片吸力面适当开设凹槽，发现凹变翼型升力系数显著增加，阻力系数略有下降。李根等[5]以NACA0012翼型为基础翼型（弦长c 为0.15m），在距翼型压力面尾缘0.1c 处加装凹槽襟翼，并发现不同厚度的凹槽襟翼均可提升翼型气动性能。韩中合和焦红瑞[6]在叶型尾部加装了Gurney襟翼，进一步改进翼型尾部形成钝尾缘，并对其气动性能进行研究。该研究发现加装钝尾缘的翼型周围的流场明显优于NACA4412原翼型流场，且改进后翼型的气动性能得到了提高。

综上所述，有效改善翼型气动性能方案虽然众多，但大多应用于风力机领域，优化翼型在飞机机翼上的应用较少。本文从加快翼尾上缘的边界层气流速度，本着减弱边界层分离的初衷，结合飞机机翼的复杂功能，以NACA4412翼型为模板，在接触面粗糙度为50μm，机翼弦长200mm，来流速度10m/s，攻角0°的基础上，提出堑尾翼型表面结构的设计方案，并进一步研究了其气动性能。采用SOLIDWORKS中的Flow Simulation模块工具对原始翼型、堑尾翼型进行数值模拟计算，对翼型改进前后的气动性能、流场分布进行对比分析。

1 理论设计与研究方法

1.1 堑尾翼的提出

来流掠过飞行器时，贴近机翼上表面处的流体微团的受力情况可以由图1表示。

微团下侧为边界层，上侧为外部非粘滞区。

在边界层的影响下，微团受到来自边界层的摩擦力f₂和来自外部非粘滞区的粘滞力f₁ 作用，产生了向前翻滚的趋势;同时，摩擦力在这一过程中占主导，使得微团逐渐降速。因此，边界层在中后段将这些微团的平动状态变为滚动状态。剧烈滚动的微团形成湍流，造成流场局部失稳的情况;速度骤减的微团也无法维持原先的较低压强，升力因此受到削弱。因此，以上这两个因素对于机翼的性能有着较大的负面影响，而这一负面影响缘于微团与边界层的长时间接触。

通过仿真模拟可以观察到，原翼型在10mps的风力环境中翼尾出现了湍流（见图2），导致机翼受到的升力呈现波动。在此影响下，机翼此时的升阻比在迭代1500次之后依然无法收敛，且平均值也较低。

综上所述，解决翼尾湍流问题并增大升阻比的根本方法就是使机翼上表面边界层对绕流的影响达到最小。本工作在这一思想下提出了堑尾翼型，如图3 所示。這种翼型在NACA4412的基础上，将尾部上缘进行了切削处理：在边界上取一点A ，在A 点正下方取一点B，与翼尾端点C 连接成一条折线，沿此折线切割进而可以得到这种翼型（A 、B 两点的确切位置将在后文进行探讨）。

当气体微团即将发生滚动时（在A 点处），其将突遇一个堑下的断崖结构（AB 段）和一个平坡（BC 段）。微团在自身惯性下保持向机翼后方流动，但在经过AB 段后的一小段时间与机翼脱离接触，因此这时的摩擦力f₂ 为零。微团在这样的结构保护下，自旋强度有所减弱，并在周围气团的粘滞力作用下，一定程度地恢复了平动的速度，有效地维持了上表面的低压。

1.2 研究方法

由于堑尾翼的形状由A 、B 两点的位置确定，因而探究最适堑尾翼型的途径即是寻找A 、B 两点的最佳位置。SOLIDWORKS 软件的FlowSimulation工具箱可以对于空间物体的平面绕流情况进行有限元分析，进而可以得到不同参数配置的堑尾翼经过迭代后的升阻比和外部流场。

本研究选用弦长为200mm 的NACA4412翼型（轮廓曲线参数由软件Profili导出）。在FlowSimulation中选用4×4m 的计算域和比率因数为10的5级网格进行1500次迭代仿真。研究将用遍历的方式得到升阻比与翼型形状（A ，B 两点位置）的数值关系。对不同流速环境下（10m/s、15m/s、30m/s、50m/s、100m/s）和不同形状的堑尾翼的气动性能进行全面探讨。选出上述工作中较优翼型，研究不同攻角的情况下其与原翼型的气动性能优劣。

2 结果与讨论

2.1 堑尾翼型的气动性能初探

现选用与C 点水平距离55mm 的A 点，和与A 点垂直距离1mm 的B 点进行模拟仿真，并假设来流速度为40m/s。

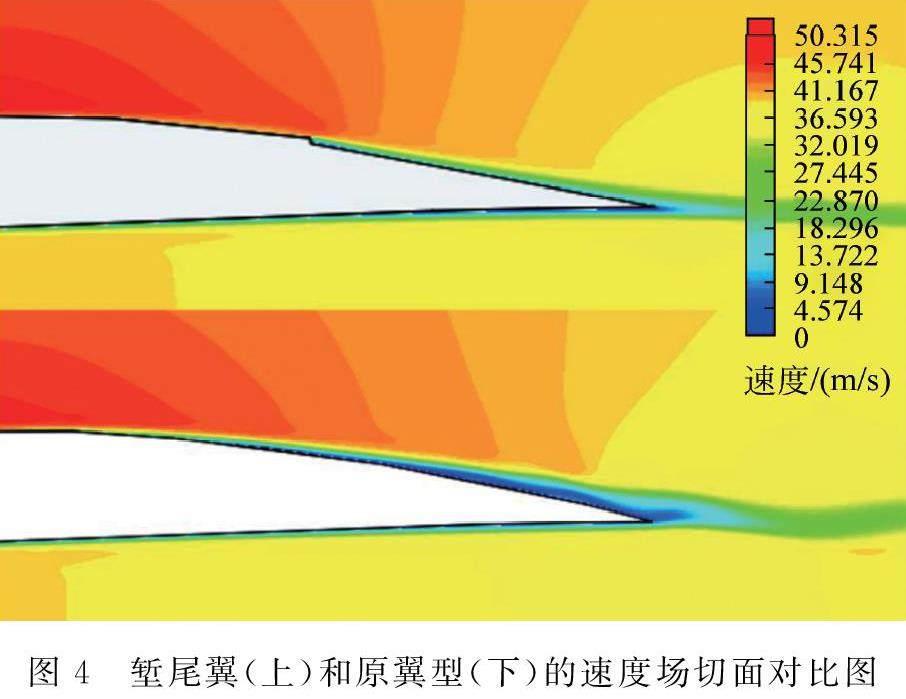
根据速度切面对比图（见图4），NACA4412原型机翼上表面气流在半程处便过早减速，继续行进的过程中，速度持续减小并诱发湍流，此时边界层发生分离（粒子迹线可参照图2）。而下方的堑尾翼型则较好地维持了上表面气流的速度，边界层始终紧贴在机翼上缘，且几乎不出现湍流。由此可见，堑尾翼能更好地限制机翼后侧的湍流，进而起到增大升阻比的作用。

对于原NACA4412翼型和基于NACA4412翼型的堑尾翼型进行仿真模拟并监视升阻比参数（见图5）。可以发现，原翼型由于伴有较强湍流，升阻比随着迭代次数（单次迭代大致对应2.5×10^-4s的物理时间）呈现较显著波动，且最终平均升阻比较低（如图中黑色点划线）。而当气流流过堑尾翼型时，分离流对升阻比的波动效果被明显削弱，并且在1500次迭代后，升阻比稳定的维持在了较高位（图中灰色虚线所示）。这体现了堑尾翼型在解决普通机翼尾部湍流问题的有效性。

2.2 中低速流场中的仿真过程

设A 点与翼尾C 点之间的水平距离是堑长x，B 点与A 点的垂直距离是堑深y，根据一般情况对堑长x 和堑深y 进行取值范围约束：50≤x≤80，0≤y≤2（单位mm）。

经表1 可发现，堑尾翼型在低速环境下（10m/s与15m/s）的气动性能相较于原翼型变化不大，且参数配置不当（A 、B 两点位置不佳）会出现负面效果;随着流速的增大（30m/s和50m/s），堑尾翼型对机翼上缘气流的转捩可以起到较好的限制作用，进而达到提高升阻比的目的;而随着风速的进一步增大（100m/s），较高速气流对翼型轮廓的变化（翼型的x、y 参数）变得更加敏感，且总体增益效果不再显著。

此处需要特别说明两点：

（1） 堑深为0mm 时不代表退化为原翼型，而是把A 、C 两点间的弧面部分切削为平面（见图6）。

（2） 这里得出的性能优良的堑尾翼型是在升阻比方面的最优翼型，而不是在去除湍流方面的最优翼型。换言之，堑尾翼型也可能存在着一些的湍流，只不过此时的小幅度湍流不主要出现在上表面，而是出现在图7中，堑尾翼型的下表面。这种小幅度湍流使得机翼升阻比呈现波动（与图5中所示情形类似），但对于平均升阻比不构成实质性负面影响。

2.3 升阻比對机翼攻角的敏感度分析

铁饼的纵向截面形状与机翼相似。研究表明，在同样初速度下投掷，选取合适的初攻角可以有效提高成绩[7];在扑克牌飞行中，当出射角较小时，出射角增加，水平位移也随之增加[8]。

受此启发，在研究了堑尾翼0攻角时的气动性能之后，本节将使用参数（堑长，堑深）为（60，0）、（65，0）、（70，0）和（75，0）的堑尾翼型来研究不同攻角下的堑尾翼型和原翼型各自的升阻比。研究依然利用SOLIDWORKS 的Flow Simulation插件，利用正交分解的方法对气流速度增加垂直的分量V_y进而模拟有攻角时的流场环境。对仿真软件得到的数据进行处理，做出了不同攻角下的平均升阻比增量，其折线对比如图8所示。

形状恰当的堑尾翼型（如图中的（65，0）和（75，0）堑尾翼型）在小攻角条件下（从0°～8°这一范围内）对升阻比的增益较为明显，对翼尾的转捩现象具有较好的抑制作用，因而具有比原翼型更出色的气动性能;而形状较不合适的堑尾翼型对于升阻比的负面影响也维持在很小的幅度。随着攻角的继续增大，原翼型和堑尾翼型气动性能急剧下降，堑尾翼的优势消失。原因在于，大攻角条件下，机翼前后缘的垂直距离较大，气流经过前缘后，较大部分气流不再继续附着于机翼表面，而是直接向后散开，远离机翼。因此，此时翼尾周围的气体流量过小，形状不同（是否下堑）对整体流场的作用不再显著。此时即将出现失速现象，因此探讨大攻角情况下的升阻比增益倍数是没有意义的。

3 结论

本文提出了对NACA4412翼型进行了优化，提出堑尾翼型，并有如下结论：

（1） 改良后的堑尾翼型与原NACA4412 翼型相比，有效地削弱了翼尾湍流，堑尾翼型升阻比最高可提升60%，由此证明了本文所提出的堑尾翼模型的可行性。

（2） 在中低速流场中堑尾翼型平均升阻比明显大于原始翼型，且随堑深减小，平均升阻比增益倍数不断增加（最高可至1.628倍）;随堑长减小，平均升阻比增益倍数总体呈现先增加后减小的趋势。堑尾翼型在30～50m/s的流速场中获得最佳性能。

（3） 在攻角为0°～8°的范围内，形状合适的堑尾翼对气动性能产生积极影响。