基于MATLAB 优化气动撑杆参数的发动机舱盖周边尺寸匹配精度改善研究

林杰 高凯 赵虎 周强 曹亚辉 柳超

摘要：基于气动撑杆引起发动机舱盖变形而导致周边尺寸匹配精度不良的问题，通过CATIA三维虚拟装配模拟分析，利用MATLAB对气动撑杆安装参数进行数值优化计算，研究出合理的发动机舱盖气动撑杆设计参数，进行相应的设计变更，并进行实车装配效果验证，使发动机舱盖周边尺寸匹配精度控制在目标范围内。针对发动机舱盖气动撑杆设计参数的变化规律，可得出以下结论：气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身后部，其弹力比a越大；气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身前部，其行程S越大；在改善气动撑杆反力导致发动机舱盖变形问题上，应尽可能将撑杆安装在发动机舱盖内板的前部区域，以减小最大压缩力。

关键词：气动撑杆 参数优化 尺寸匹配精度 发动机舱盖 MATLAB数值计算

中图分类号：U462.1   文献标识码：B   DOI： 10.19710/J.cnki.1003-8817.20220418

Abstract： In this paper， based on the poor dimension matching accuracy of engine hood caused by the deformation of gas springs acting on the hood， through the simulation analysis of CATIA three-dimensional virtual assembly， and using MATLAB to numerically optimize the installation parameters of gas springs， reasonable design parameters of gas spring were worked out， and then corresponding design changes were made， and the assembly effect on the real vehicle was verified， controlling the dimension matching accuracy of engine hood within the target range. For the design parameters change law of the engine hood gas springs， the following conclusions can be drawn： （1） the more front gas springs are installed on the engine hood， and the more backward gas springs are installed on the vehicle body， the larger the elastic force ratio of gas springs is; （2） the more front gas springs are installed on the engine hood， and the more front gas springs are installed on the vehicle body， the larger its travel S is; （3） in order to improve the deformation problem of the gas springs acting on engine hood， the gas springs should be installed as front as possible on the engine hood， on account of reducing the maximum compressive force.

Key words： Gas spring， Parameter optimization， Dimension matching accuracy， Engine hood， MATLAB numerical calculation

1 前言

隨着汽车电动化和智能化转型升级，用户对汽车外观造型和内外饰匹配质量的要求日益提高[1]。市面上SUV、MPV、轿车等车型逐步采用气动撑杆（气弹簧）作为发动机舱盖和行李舱尾门开启和关闭功能的关键零部件[2]。而气动撑杆是由一个密闭缸筒和可在缸筒内滑动的活塞及活塞杆组件组成的以氮气或其它惰性气体为储能介质的弹性元件[3]。在装配气动撑杆后，在较大的气动撑杆反力作用下，被支撑零件会产生局部变形，衍生出外观尺寸和功能性问题[4]。

针对汽车气动撑杆设计中的力学问题，Tiwari等[5]建立了气动撑杆的全结构有限元模型，用来检查通过逆向工程的门升降/关闭安全系数设计，可以达到减轻质量和降低安全系数余量的目的。Lee等[6]针对尾门气动撑杆结构，分别利用软件提供的二次朗格朗日非线性规划和遗传算法进行参数优化，确保了设计过程的可靠性，验证了模拟模型和提出最佳算法的有效性。Park等[7]利用通用有限元软件ANSYS从传热学角度对双金属结构的气动撑杆进行分析，得出了随温度变化双金属撑杆在不同工况下的工作原理，总结了总变形量随金属直径、双金属角度变化规律，并认为可以根据双金属尺寸和角度变化来确定设计中温度补偿量。

安康等[8]以轿车后背门为例，利用三维CATIA软件，分析了气动撑杆力与力矩的关系，从功能性出发给出了气动撑杆参数设计方法。单莉娟等[9]通过对气动撑杆结构静力学和运动学分析，研究了安装点位置变化对开启条件的影响，提出了关闭状态下后背门与死点线夹角关系规律，为安全可靠的气动撑杆设计提供了理论依据。孙相龙等[10]针对气动撑杆导致后举门变形问题，分别从整体位移、局部反变形补偿、扰流板局部变形方面研究了工程方案，系统性解决实车尺寸匹配问题。智文静等[11]为了优化气动撑杆参数，运用余弦定理和MATLAB软件对撑杆进行设计仿真，计算出了不同阻尼孔直径下应急舱门的开启时间。

在汽车智能化趋势下，气动撑杆的普及是必然趋势[12]。另一方面，前脸区域又是尺寸感知质量敏感区域，引入气动撑杆会带来前脸区域外观尺寸匹配问题，需要合理的气动撑杆设计参数来保证实车尺寸匹配精度[13]。

本文以某SUV新车型试制过程中气动撑杆导致发动机舱盖周边尺寸技术规范（Dimensional Technical Specification，DTS）设定目标未达成为背景，通过CATIA虚拟装配仿真和MATLAB数值计算，结合前期试验数据，优化了气动撑杆的设计参数，并在后续试制阶段进行了效果验证。

2 问题现状

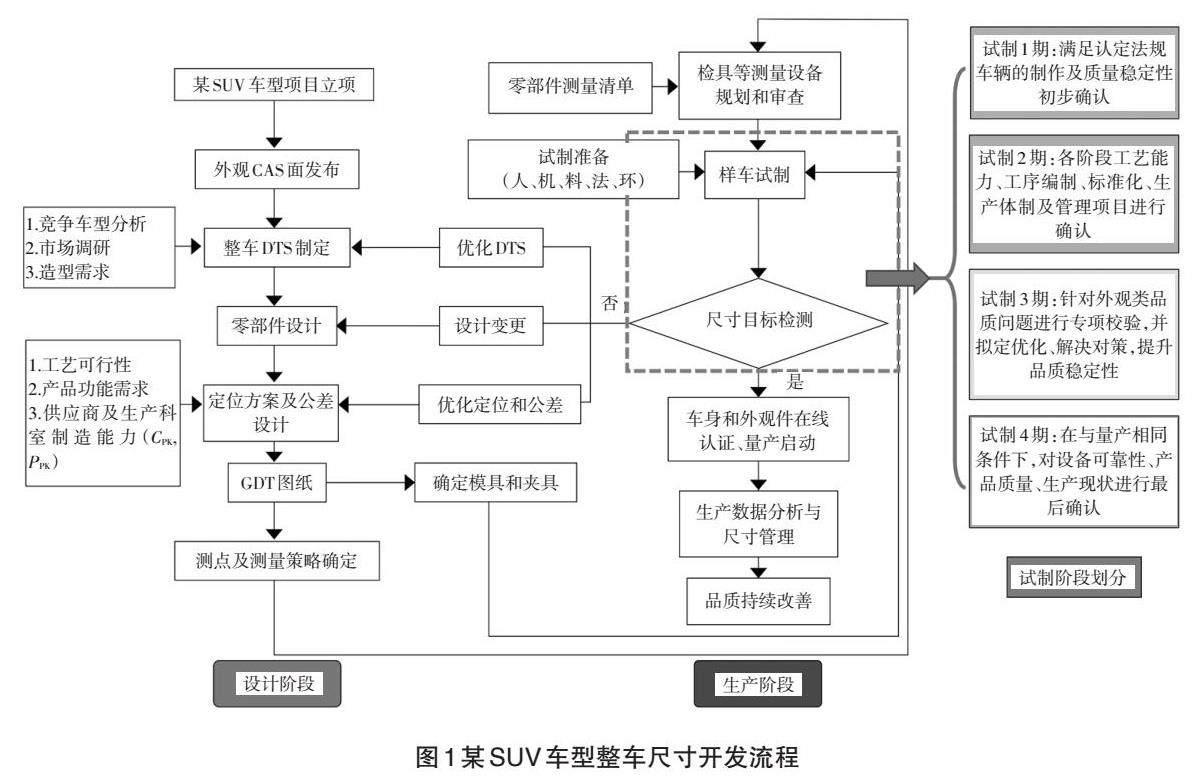
针对用户不同的需求，某品牌会对量产车型进行大、中、小改款。图1是针对改款车型的整车尺寸开发流程，根据不同试制目的，将试制期分为4个阶段，分别为试制1期、试制2期、试制3期及试制4期。试制4期之后是量产准备期，之后是正式量产。

该中期改款SUV车型在完成模具、夹具及检具的工程审查后，在试制1期的首批10台份车辆中，发动机舱盖周边DTS达成度不足频发。主要表现为发动机舱盖与翼子板、发动机舱盖与大灯、发动机舱盖与前保险杠等配合部位的面差值逆向超差；其次是相关部位间隙值相对设计阶段的基准值偏大，发动机舱盖与翼子板配合部位的尺寸匹配问题最为显著，影响了产品的视觉感知质量，增大了车辆功能性故障风险。DTS测量成绩如表1所示，图2为DTS测量点点位图。从中可以发现，面差实测值相比设定基准值普遍存在逆向超差，即发动机舱盖凸出，在气动撑杆的前端测点8和测点9处表现最为明显，整条E线（测点4～12边线）面差波动为2.3～3.4 mm。

3 参数优化设计

3.1 结构分析及优化思路

气动弹簧可分为压缩气动撑杆、拉伸气动撑杆、可锁定气动撑杆、座椅升降气动撑杆。该SUV车型发动机舱盖撑杆采用的是带阻尼孔的压缩气动弹簧，即无外力作用时活塞杆呈自由伸展状态，工作中始终承受压力，其由活塞杆、密封圈、润滑油、压力管、活塞、阻尼孔和导向件组成，工作原理如图3所示。

压缩型气动撑杆的力-位移曲线如图4所示，可分为压缩过程和伸展过程。压缩过程撑杆反力由F3逐渐增大至F4，伸展过程撑杆反力由F2逐渐减小至F1，Fa和Fb为公称力，C1为行程两端的非采力长度，S为气动撑杆行程，气动撑杆设计参数参照GB/T 39433—2020《气弹簧设计计算》[14]执行。

发动机舱盖通过铰链与车身连接，其左侧铰链旋转中心为O，右侧为[O]，发动机舱盖的开闭过程即为发动机舱盖绕轴线[O]旋转的过程，如图5所示。旋转角度为q，A为撑杆在发动机舱盖上的安装点，B为撑杆在车身上的安装点，C为发动机舱盖质心坐标点，F为撑杆弹力，f为撑杆摩擦力，m为发动机舱盖总成质量，G为发动机舱盖总成所受重力，MF、Mf、MG分别为气动撑杆弹力力矩、撑杆摩擦力矩、发动机舱盖重力力矩。

在打开发动机舱盖锁的1st开关后，发动机舱盖会弹起一个角度，根据锁的模型参数确定这个角度θ1=1.15°，此时重力矩大于撑杆弹力力矩，锁会通过锁扣对发动机舱盖施加向上的反向力Ffan，此时发动机舱盖在重力力矩MG、气动撑杆弹力力矩MF、摩擦力矩Mf和反向力力矩Mfan的作用下处于平衡状态。当打开发动机舱盖锁的2st开关后，人手施加初始力，反向力力矩Mfan逐渐减小至0，在人手力矩Mren作用下，发动机舱盖逐渐打开，最大开启角度θmax=42°。

已知参数如下：发动机舱盖重力G=184.4 N，发动机舱盖质心坐标C=（-366.56，0，687.98），铰链旋转中心[O]坐标为（330.5，±755.4，750），发动机舱盖关闭状态下θ=0°，发动机舱盖最大开启角度θ=42°。优化前撑杆在发动机舱盖上安装点A0=（-243.46，-682，664.31），优化前撑杆在车身安装点B0=（42.92，-751.93，651.6）。根據气动撑杆设计标准及人机工程学要求，在设计阶段提出气动撑杆参数要求如下：伸展长度L=463 mm，缸筒长度B=221.9 mm，设计行程S=174 mm，F1=250 N，F4≤390 N，Fr≤45 N。

本文撑杆优化思路是基于发动机舱盖重力力矩MG、弹簧弹力力矩MF、撑杆摩擦力矩Mf在开闭过程中随旋转角度q的变化规律，结合人机工程学要求，在发动机舱盖和车身上选择合适的气动撑杆安装点，并给出最优气动撑杆设计参数，使得撑杆在关闭状态下的撑杆反力沿发动机舱盖加强板所在面法向的投影值F4-tou最小，从而最大限度削减气动撑杆弹力对发动机舱盖周边DTS的影响。具体的优化流程如下：

a. 气动撑杆在发动机舱盖上可供选择的安装点A需分布在发动机舱盖加强板所在面上，以加强板端部Y向中点和优化前撑杆在发动机舱盖安装点A0的连线构造出空间直线1，撑杆在发动机舱盖上安装点的优化在直线1上进行数值计算，每隔2.4 mm选取一个点，共200个优化参考点。

b. 气动撑杆在车身上可供选择的安装点B需随着轮罩轮廓分布，通过支架进行焊接，以优化前的撑杆在车身上安装点B0为参考，构造出过B0点Y平面与轮罩上曲面的交线，将交线以最短距离平移至点B0，得到空间曲线2，在空间曲线2上进行数值计算，每隔2.6 mm选取一个点，得到200个优化参考点。气动撑杆安装的可优化点示意如图7所示。

c. 针对A点、B点组成的40 000组优化参考点进行力学校核：以矩阵为计算单元，旋转角度q为函数，通过公式（1）三维空间点绕轴旋转公式得出A点随q变化表达式、质心随q变化表达式、MG随q变化表达式，旋转角度增量[Δθ=0.2°]，根据A点、B点距离的变化确定该组设计的L和S。根据撑杆的设计要求，当θ=0°时，撑杆长度最短；当θ=42°时，撑杆长度最长，即可初步剔除不合理设计点。

三维空间点P（Px，Py，Pz）绕任意轴旋转角度α0得到新点[P（P′x，P′y，P′z）]。轴线单位方向向量为[n（n2x+n2y+n2z=1）]，过点Q0（x0，y0，z0）。点[P]与P之间满足如下关系：

d. 当θ=1.15°时，MG=128.70 N·m，不同设计不影响重力力矩，为确保不同设计人施加的力矩相同Mrcn=101.16 N·m，则使每组设计MF+Mf不变即可。取10台份试制车辆的撑杆，测试摩擦力并求平均值Fr=27.1 N，由此可计算出每组设计的F2。当θ=42°时，MG=103.16 N·m，确保撑杆弹力力矩大于重力力矩，取MF=149.5 N·m，可计算出每组设计的F1。

e. 根据每组设计的L、S、F1、F2和Fr，计算当θ=0°时最大压缩力F4在发动机舱盖加强板所在面法向上的投影值F4-tou，面法向向量n=（-0.1，0.1），如图6所示。使F4-tou取最小值来削减撑杆对发动机舱盖周边外观尺寸的影响，同时参考气动撑杆设计标准，以每组设计的弹力比为1.0<α<1.5、行程S≤200 mm、伸展长度与行程比值L/S>2.0作为约束条件，并结合设计变更费用、装配干涉因素，综合选取合理的撑杆安装点。

3.2 计算结果及分析

每一组撑杆安装点可用自变量X和Y来表征：X值表示直线1上A点到右侧端点的距离，Y值表示曲线2上B点到右侧端点的距离。例如，优化前撑杆安装点由A0和B0决定，可用图11中初始点表示。采用编程实现3.1节中数值计算过程，对计算结果进行处理。图7～图10分别为最大压缩力投影值F4-tou、弹力比a、行程S、伸展长度与行程比值L/S随撑杆安装点的变化趋势。由图7的等高线可知，最大压缩力投影值F4-tou随着X的增大而减小，而Y值对F4-tou影响不明显。这表明撑杆在发动机舱盖上的安装点A越靠前，F4-tou越小，撑杆对发动机舱盖产生的变形量越小，而撑杆在轮罩上的安装点B对F4-tou影响不明显，因此，应尽可能的将撑杆安装在发动机舱盖内板的前部区域。

如图8所示，根据弹力比设计要求，分别用Z=1.0和Z=1.5的平面截取弹力比曲面，将得到空间曲线投影到XY平面，撑杆安装点应分布在“弹力比限定区”的封闭区域内。可以看出，气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身后部，弹力比a越大。同理，针对行程设计要求，合理的撑杆设计点应分布在图9所示的“行程限定区”梯形区域内。可以看出，气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身前部，行程S越大。针对伸展长度与行程比值L/S的设计要求，合理的撑杆设计点应分布在图10所示的三角形区域内。

对上述3个区域取交集，交集区域内部的点同时满足上述要求的设计点。图11为撑杆安装点优化的平面示意，重叠域内的点是满足约束条件的设计点，其中初始点位表示优化前的撑杆安装点，其弹力比为1.33。为使X尽量大，可考虑适当增大弹力比来优化撑杆安装点，取优化后的弹力比为1.4，求弹力比为1.4曲线与行程线的交点，取该点为优化后的撑杆安装点，并在CATIA中进行干涉性检查。

优化后的撑杆安装点XY坐标为（320，98），其对应的撑杆安装点在车身坐标系下的坐标值分别为Aopt=（-338.168，-680.326，650.429），Bopt=（-10.1876，-751.93，642.5258），。如图7所示，优化后的撑杆力投影值为108.65 N，相比优化前的撑杆力投影值135.19 N削减约20%。

3.3 优化后气动撑杆参数

根据3.2节计算结果，确定优化后气动撑杆参数如表2所示。

面向制造商提出的技术参数要求如下：材料：缸筒采用20#钢管，活塞杆采用45#钢；伸展长度L=（535±2） mm；设计行程S=199 mm；F1=213±10 N，F4≤371 N，Fr≤40 N；力学特性、疲劳寿命、耐腐蚀性和压缩气体性能参照原产品标准书进行执行。

4 效果验证及讨论

4.1 效果驗证

4.1.1 发动机舱盖有限元受力分析

为在设计变更前初步预测和验证优化前后气动撑杆反力对发动机舱盖的变形量，利用有限元程序建立仿真模型，如图12所示。仿真部件采用发动机舱盖总成中包含的所有零件，内外板边缘部分及内部与加强版配合区域采用焊接单元进行联结，材料采用同种钢材料的材料参数，模拟包边扣合工艺；中间涂胶区域采用刚性连接，不考虑内外板之间相对位移。边界条件如下：建立铰链配合区域结点与中心结点的刚性耦合，固定中心结点5个方向（1、2、3、4、6）的自由度，仅放开沿Y轴旋转自由度，模拟发动机舱盖的开闭；固定前部与锁配合锁扣的中心结点3个方向自由度，模拟发动机舱盖关闭扣合的状态。在舱盖内外板上分别建立优化前后气动撑杆安装部位螺栓法兰面结点集合，结点集分别与圆形法兰面中心结点建立刚性耦合，对中心结点分别沿着优化前后气动撑杆反力方向施加所对应的撑杆力。

图13和图14分别为优化前后撑杆力对发动机舱盖变形的云图，提取其中发动机舱盖边缘E线结点沿Z方向的位移，分析其沿X方向的变化趋势，如图15所示。可知，优化前沿Z方向最大位移发生在X=-334.41处，最大凸出量为1.02 mm；优化后沿Z方向的最大位移量发生在在X=-504.67处，最大凸出量为0.42 mm，发动机舱盖的凸出变形量削减了58.8%。然而，前述3.2节中计算撑杆力投影值的削减为20%，所以可认为沿Z方向的变形量与施加撑杆力成非线性相关。

仿真模型是在线性基础上建立的，上述非线性变化规律由结构变化导致：一是气动撑杆安装点优化后，发动机舱盖受力点、受力方向、受力大小发生变化；二是发动机舱盖内板和外板形状上均为越靠近前部，其Z向坐标值越低，呈下倾趋势，外板前部向里侧收拢，导致前部作用力引起的变形更难传递到外观上。

4.1.2 气动撑杆设计变更后实车换装

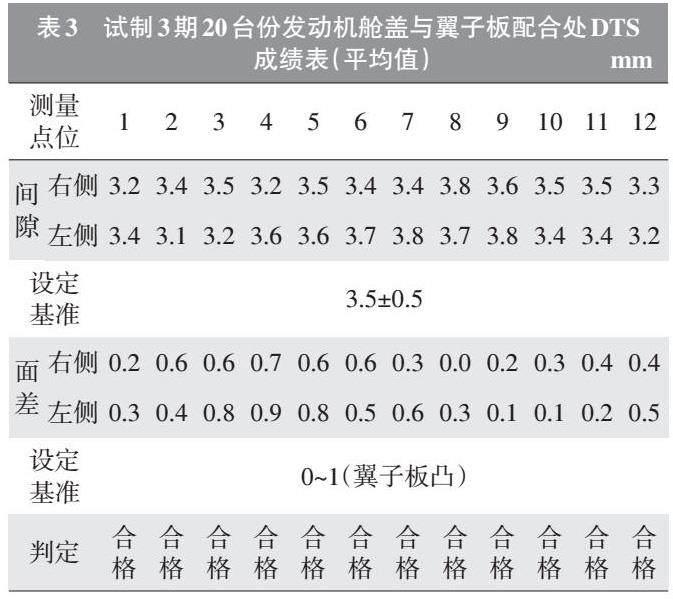
参考第3.3节中气动撑杆优化结果，对气动撑杆、发动机舱盖内板和车身轮罩进行相应的设计变更，在试制4期装配的20台份试验车上进行批量装车验证，平均成绩见表3，12处测量点位的面差值和间隙值均达到基准范围内。

试制1期时，间隙值超差的主要原因是面差值超差，发动机舱盖与翼子板的配合面并非水平面，而是呈45°的倾斜面，所以Z向变形也会影响间隙值。优化了气动撑杆参数后，发动机舱盖受力变小，面差值得到大幅改善，间隙值相应减小。为对比气动撑杆参数优化后的效果，可重点关注测点8和测点9相比其它测点面差值的变化量，测点8和测点9处发动机舱盖仍然高出测点4～测点7和测点10～测点12，但整条E线面差波动在0.7～0.8 mm，远小于最初的波动量2.3～3.4 mm。

4.2 结果讨论

汽车外观尺寸的匹配精度受多种因素影响，如各层级钣金件精度、焊接后白车身精度、夹/治具精度、作业员装配偏差[15]。在此次SUV新车型的试制导入过程中，针对发动机舱盖周边尺寸匹配精度问题，除应用上述气动撑杆参数优化的对策外，还研究和实施了发动机舱盖内板反变形补偿调整、翼子板支架设计变更、前端模块（Front-End Module，FEM）上装治具调整优化对策。

a. 反变形补偿调整。如孙相龙等[10]所述，在解决包括撑杆在内的发动机舱盖非均匀变形的问题上，反变形补偿调整是较为常用的做法。本文在确定反变形补偿量时除参考气动撑杆影响量外，还针对涂装工艺导致的发动机舱盖烘烤热变形量进行了测量，发现热变形规律与撑杆反力变形的规律类似，易对发动机舱盖中前部造成约0.6 mm的凸起。最终对发动机舱盖内板修模调整了0.5 mm，总成件精度改善约为0.3 mm。

b. 翼子板支架设计变更。在试制初期，除发动机舱盖非均匀变形外，翼子板因轮罩上与翼子板配合支架精度偏差导致其整体下沉量约为2 mm，后续通过支架设计变更，并配合夹具调整，优化了翼子板安装后整体精度，恢复到理论位置向上0～0.5 mm。

c. FEM上装治具调整。发动机舱盖前部通过锁与FEM连接，而FEM总成具有包含零件种类多、上装工序复杂、质量大特点，因装配偏差和重力下沉导致的翻转会通过锁传递到发动机舱盖前部，致使其前部向下偏1.5 mm。在试制3期各层级零件精度稳定之后，最终通过对上装治具进行再优化和调整，改善了FEM前部翻转性能。

从具体事项的尺寸链分析来看，尺寸链中每一环均会有偏差来源。目前，解决尺寸匹配精度问题较为普遍的做法是通过公差分析软件进行计算，明确偏差来源中贡献度较大的项目，分别从中值调整和散差管控两个方向进行研究和施策。其中，针对刚性零部件（变形小，可近似看做刚体）尺寸偏差仿真计算较为成熟。但是针对可变形零件，要将各种复杂因素导致的变形准确地反应到尺寸链计算中，使得计算结果能够在整车厂进行大范围推广和应用比较是比较困难的。

本文气动撑杆参数优化是研究和改善发动机舱盖局部不均匀变形的方向之一，如果需要持续削减气动撑杆作用于发动机舱盖的局部不均匀形变对尺寸匹配精度的影响，未来可考虑从发动机舱盖的整体刚性试验和仿真着手，继续优化内板结构和提升材料性能，以提高发动机舱盖整体抗变形能力[16]。

5 结束语

本文基于气动撑杆引起发动机舱盖变形因而导致其周边尺寸匹配精度不良的背景，通过CATIA三维虚拟装配模拟分析，结合MATLAB对气动撑杆安装参数进行数值计算，研究出了合理的发动机舱盖气动撑杆设计参数，然后进行相应的设计变更，并在实车上进行装配效果验证，使得发动机舱盖周边尺寸匹配精度得到大幅改善。

本文提出的气动撑杆参数数值优化方法具有一定的推广作用，该方法可覆盖空间所有三维安装点，其优化的目标函数也可转换为其它所需的撑杆参数或者设计中所需的构造函数。在新车型设计和试制中，此优化方法不仅对其它具有气动撑杆车型品质问题的解决具有借鉴意义，还能为解决气动撑桿开闭和干涉验证、人机工程等机能问题的气动撑杆设计提供思路。针对气动撑杆参数优化变化规律，可以总结出以下结论：

a. 气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身后部，其弹力比a越大；

b. 气动撑杆安装位置越靠近发动机舱盖前部，越靠近车身前部，其行程S越大；

c. 在改善撑杆反力导致发动机舱盖变形问题上，应尽可能的将撑杆安装在发动机舱盖内板的前部区域，以减小最大压缩力。

参考文献：

[1] 罗帅， 彭杨， 张磊， 等. 气弹簧力导致后举门变形的有限元模拟方法[J]. 汽车零部件， 2018（6）： 67-69.

[2] TIWARI S， GAUTAM A V. A Review on Gas Spring & Application in Industry[C]// AIP Conference Proceedings. AIP Publishing LLC， 2022.

[3] 孔令猛. 气弹簧选型的设计思路[J]. 商用汽车， 2012（20）： 99-101.

[4] 王天利， 李明杰， 孙晓帮， 等. 车用气弹簧力学性能仿真研究[J]. 农业装备与车辆工程， 2009（2）： 3-5+20.

[5] TIWARI S， GAUTAM A V. FEA Analysis of Gas Spring Design[C]// AIP Conference Proceedings， AIP Publishing LLC， 2022.

[6] LEE C T. A Study on the Optimal Design of Automotive Gas Spring[J]. Journal of Drive and Control， 2017， 14（4）： 45-50.

[7] PARK C W， KIM H Y. A Study on the Auto-Moblie Gas Spring Structural Analysis Using of Bimetal[J]. Journal of the Korean Society of Manufacturing Technology Engineers， 2013， 22（1）： 131-137.

[8] 安康， 毛春升， 盛勇生. CATIA的汽车后背门气动撑杆参数设计[J]. 汽车工程师， 2010（6）： 30-32.

[9] 单莉娟， 刘同金， 肖洪波，等. 基于CATIA的轿车后背门气动撑杆参数设计[C]// 中国汽车工程学会汽车安全技术学术会议. 中国汽车工程学会， 2013.

[10] 孙相龙. 气弹簧力导致某SUV车型后举门变形的分析与解决[J]. 汽车实用技术， 2020（12）： 148-150.

[11] 智文静， 郑维娟， 陈安婷， 等. 基于余弦定理和Simulink的气弹簧建模与仿真研究[J]. 测控技术， 2022， 41（3）： 95-100.

[12] 侯林， 史承婕， 王鹏， 等. 气弹簧助力式四连杆铰链发动机罩的计算与优化分析[J]. 汽车技术， 2021（7）： 52-57.

[13] 洪海玻， 魏庆丰， 杜坤. 汽车前脸外观尺寸控制方案[J]. 汽车工艺师， 2021（12）： 39-10+43.

[14] 全国弹簧标准化技术委员会. 气弹簧设计计算： GB/T 39433—2020[S]. 北京： 中国标准出版社， 2020.

[15] 刘武生， 陈学军， 叶勋， 等. 尺寸工程匹配阶段实物评估方法[J]. 机电技术， 2020（2）： 49-53.

[16] 谢绍龙. 基于ABAQUS的某SUV引擎盖力学性能仿真与试验研究[J]. 汽车实用技术， 2020， 45（19）：179-180+192.