基于FCM-AHP方法的加工中心典型测试工况优选

聂新宇 吴波 侯金龙 陈阳

摘要：针对传统载荷谱典型测试工况选取方法中存在的问题，通过模糊聚类分析挖掘工艺参数间潜在关系，实现了工况数据分类初选，同时充分考虑了分类过程的模糊性并且避免了方案初选的主观随意性。在初选结果基础上引入层次分析法，综合考虑测试工况选取的典型性、全面性、试验开展的经济性以及编谱数据量4个综合评价指标，建立了系统层次结构模型，将定性分析和定量计算相结合，选取了具有代表性的测试工况，从而提高了典型测试工况选取的科学性和系统性。

關键词：载荷谱 典型测试工况 模糊聚类分析 层析分析法

中图分类号：U466   文献标识码：B   DOI： 10.19710/J.cnki.1003-8817.20220306

Abstract： To solve the problems existing in the selection method of typical test conditions of the traditional load spectrum， this paper explored the potential relationship between process parameters by fuzzy clustering analysis， and realized the classification and primary selection of operating conditions data， meanwhile， the fuzziness of the classification process was fully considered and the subjective randomness of the preliminary selection of the scheme was avoided. On the basis of the preliminary selection results， the Analytic Hierarchy Process （AHP） was introduced to comprehensively consider the 4 comprehensive evaluation indexes， namely， the typicality and comprehensiveness of the selection of test conditions， the economy of the test and the amount of spectral data. The hierarchical structure model of the system was established， and the representative test conditions were selected by combining qualitative analysis and quantitative calculation， thus improving the scientificity and systematization of the selection of typical test conditions.

Key words： Load spectrum， Typical test condition， Fuzzy cluster analysis， Analytic Hierarchy Process （AHP）

1 前言

数控机床载荷谱作为提高数控机床可靠性水平的重要手段，不仅能够为数控机床整机及其关键功能部件可靠性设计提供客观依据，还能够为数控机床可靠性试验提供模拟加载依据[1]。典型测试工况的选取作为载荷谱编制的关键技术之一，其选取的准确性直接影响着载荷谱编制的正确性和应用效果[2]。因此，如何选取具有典型性和代表性的测试工况一直是载荷谱编制的热点问题。

在数控机床领域，典型测试工况需要根据机床的类型确定典型的加工形式、加工工艺及其时间比例。目前，常见确定典型工艺参数方法[3]分为3种：基于统计的正交性原理，采用正交试验选择具有代表性的试验工况；基于切削工艺参数及其加工时间，建立工艺参数的概率密度函数从而完成对典型工况的选取；通过现场工艺数据利用切削载荷经验公式计算切削载荷，求解切削载荷的概率密度函数，将其概率密度函数划分多个区间，选取区间中位点对应的工艺参数作为典型测试工艺。传统方法存在一些不足和缺陷，例如正交试验选取的工艺参数组合可能为生产实践中不常见的工艺参数组合，缺乏代表性；通过切削载荷经验公式计算获取的切削载荷为静态载荷，与真实动态载荷的情况差异较大，且通过区间中点选取工艺参数具有随机性；典型测试工况选取过程中未考虑各个工艺参数间的潜在关系和分类过程的模糊性[4]，同时也未综合考虑工艺参数的典型性、测试试验的经济性以及测试数据量。

为解决上述问题，本文将典型测试工况选取视为模糊分类问题，通过采用F统计量对分类阈值[λ]进行初步确定，从而得到模糊聚类的初始分类簇数，再引入层次分析法建立多方面综合评价指标，主客观确定各因素权重[5]，从而优选典型测试工况方案。

2 研究方法

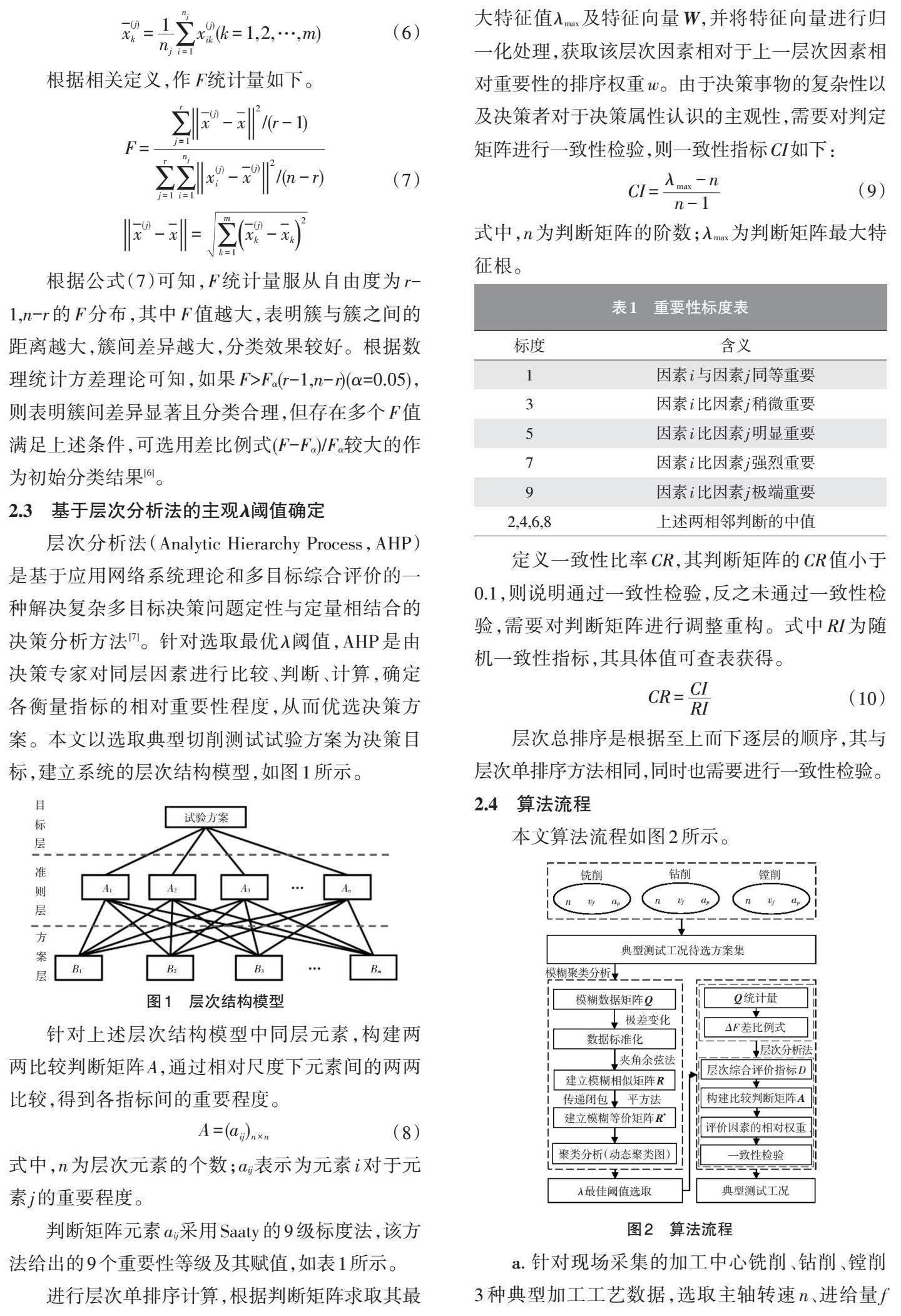
2.1 模糊聚类分析

模糊聚类（Fuzzy Cluster Analysis，FCM）分析模型是一种基于划分的多元分析方法，其算法一般步骤可分为数据标准化处理、标定（建立模糊相似矩阵）和聚类（求动态聚类图）[6]。

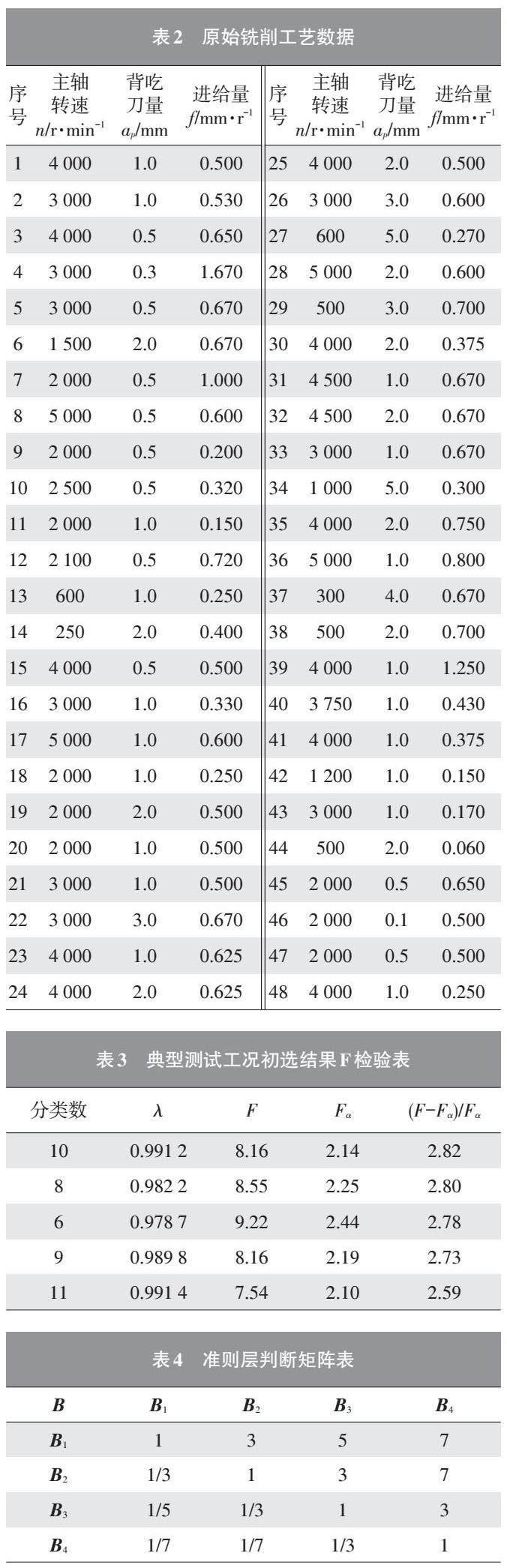
2.4 算法流程

本文算法流程如图2所示。

a. 针对现场采集的加工中心铣削、钻削、镗削3种典型加工工艺数据，选取主轴转速n、进给量f以及背吃刀量ap构建典型测试工况待选方案集A。

b. 采用模糊聚类分析获得工艺参数动态聚类图。

c. 计算各分类结果的F统计量进行显著性检验，并在分类效果显著的分类结果中选择差比例式（F-Fα）/Fα较大者作为初始分类结果。

d. 按照层次分析法中选取尽量少的指标反映最主要和最全面信息的选取原则，从典型性、全面性、经济性及数据量方面，确定典型工况选取层次综合评价指标：B={T，G，E，D}。T表示典型性，G表示全面性，E表示经济性，D表示数据量。

e. 采用层次分析法计算各元素的权重系数，通过比较各元素的权重系数，优选决策方案，并选取分类簇中加工时间占比大的工艺参数组合作为加工中心的典型测试工况参数组。

3 计算实例

本文以加工中心现场48组铣削工艺数据为例，采用上述方法对加工中心的典型测试工况进行优选。现场采集的原始铣削工艺数据如表2所示。

首先，对现场采集的48组原始铣削工艺数据进行模糊聚类分析，获得工艺参数的动态聚类图，进一步计算分类结果F统计量，对分类结果进行显著性检验，在聚类分析显著的结果中选择差比例式（F-Fα）/Fα较大值为对应的初始分类结果，则初选分类结果F检验表如表3所示。

按照层次分析法的相关步骤和规则，将上表典型测试工况的初选结果作为方案层A（分别用A1～A5表示），并将影响方案确定的主要因素T、G、E、D（分别用B1～B4表示）作为层次综合评价指标B，通过行业专家对各个因素重要程度进行两两比较，获得准则层判断矩阵，如表4所示。

依据准则层判断矩阵，通过方根法确定准则层各因素对目标层的相对权重，其权重向量为[WTB=（0.553 5，0.281 2，0.115 6，0.049 7）]，进行一致性检验，CI=0.004 6，CR=0.052（<0.1），满足一致性检验。

通过构造方案层因素对准则层中典型性、全面性、经济性及数据量5个因素的成对比较矩阵，如下所示。

采用方根法[8]求解方案层因素对准则层每一元素的相对权重[WA/Bi（i）=1～4]，并对每一个判断矩阵进行一致性验证，其计算结果如表5所示，由下表可知上述4个判断矩阵CR值均小于0.1，一致性可以接受。

确定方案层对目标层的组合权重，并进行层次总排序，各方案层权重值如表6所示。选取A5={4、6、13、19、20、23、25、27、38、42、44}为典型测试工况。

4 结论

a. 相比于传统典型测试工况选取方法，通过模糊聚类分析方法挖掘出各工艺参数间潜在关系，充分考虑分类过程中存在的模糊性，对分类结果进行F检验，获得典型测试工况初选结果，提高了典型测试工况选取的科学性。

b. 在初选结果基础上，引入层次分析法建立典型性、全面性、经济性及数据量4方面综合评价指标，引入专家决策主观评价因素，得到合理的权重矩阵，该方法较好地解决了多因素综合决策问题，通过科学合理决策优选典型测试工况方案。

c. 层次分析法作为一种定性与定量相结合的决策分析方法，避免单纯定量分析对工艺参数数据的依赖性，通过多种方案在多种评价指标下的比选，使得典型测试工况方案选择更加合理化和系统化。

参考文献：

[1] 杨兆军， 陈传海， 陈菲， 等. 数控机床可靠性技术的研究进展[J]. 机械工程学报， 2013， 49（20）： 10-10.

[2] 何佳龙. 数控车床切削力谱的编制及其在功能部件可靠性试验中的应用[D]. 长春： 吉林大学， 2017.

[3] 王升旭. 数控车床非平稳动态切削力谱的编制[D]. 长春： 吉林大学， 2021.

[4] 谢季坚， 刘承平. 模糊数学方法及其应用[M]. 武汉： 华中理工大学出版社， 2005.

[5] 常建娥， 蒋太立. 层次分析法确定权重的研究[J]. 武汉理工大学学报： 信息与管理工程版， 2007， 29（1）： 4-4.

[6] 梁保松， 曹殿立. 模糊数学及其应用[M]. 北京： 科学出版社， 2007.

[7] 宋久鵬， 董大伟， 高国安. 基于层次分析法和灰色关联度的方案决策模型研究[J]. 西南交通大学学报， 2002， 37（4）： 463-466.

[8] 吴文江. 基于方根法三阶判断矩阵一致性检验的准确性[J]. 建筑材料学报， 1994， 7（1）： 44-46.