直击随机变量及其分布中的数学思想
■河南大学附属中学 陈啸宇
数学解题,必须讲究思想方法,随机变量及其分布问题也不例外。那么在解决这个内容的问题时,我们会遭遇哪些数学思想呢?本文举例说明。
一、数形结合思想
例1(多选)设随机变量X~N(2,9),且P(X<3a-1)=P(X>a2+1),则实数a的值可能为( )。
A.0 B.1 C.2 D.-4
解析:因为随机变量服从X~N(2,9),所以正态曲线关于直线x=2对称。
因为P(X<3a-1)=P(X>a2+1),所以3a-1+a2+1=4,解得a=1或-4。
故选BD。
点评:对于正态分布问题,一般可根据正态分布曲线的对称性来求解,利用的数学思想就是数形结合思想。
二、函数思想
例2在一次新兵射击能力检测中,每人都可打5枪,只要击中靶标就停止射击,合格通过;5次全不中,则不合格。新兵A参加射击能力检测,假设他每次射击相互独立,且击中靶标的概率均为p(0<p<1),当p=p0时,他至少射击4次合格通过的概率才最大,则p0=_____。
解析:至少射击4 次合格通过的概率为f(p)=(1-p)3p+(1-p)4p=(1-p)3·(2p-p2)。
所以f'(p)=(1-p)2(5p2-10p+2)。
点评:用f(p)表示至少射击4次才合格通过的概率,并利用导数研究f(p)在(0,1)上的最值即可。
三、分类讨论思想
例3边长为2的正方形ABCD的中心为O,从A、B、C、D、O这5个点中任意选2点,以其中一点为起点、另一点为终点作向量,任取其中两个向量(不包括“向量和同端点的相反向量”),以它们的数量积的绝对值作为随机变量X,则其数学期望E(X)=_____。
点评:本题关键点有两点,一个是随机抽取向量时,基本事件的总数;另一个是抽取后,计算抽取向量的数量积的绝对值的可能情形,必须做到不重不漏。
四、转化思想
例4现在甲、乙两个靶,某射手向甲靶射击一次,命中的概率为,命中得1 分,没有命中得0分;向乙靶射击两次,每次命中的概率为,每命中一次得2分,没有命中得0 分。该射手每次射击的结果相互独立,假设该射手完成以上三次射击。
(1)求该射手恰好命中一次的概率;
(2)求该射手的总得分X的分布列。
解析:(1)设“该射手恰好命中一次”为事件A,“该射手射击甲靶命中”为事件B,“该射手第一次射击乙靶命中”为事件C,“该射手第二次射击乙靶命中”为事件D。
(2)根据题意知,X的所有可能取值为0,1,2,3,4,5。
根据事件的独立性和互斥性,得:
故X的分布列如表1。
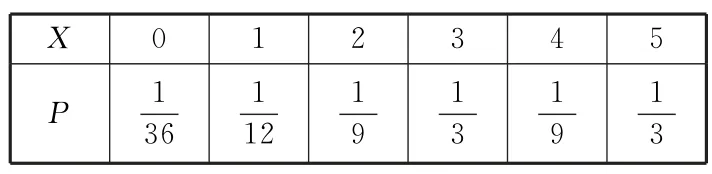
表1
点评:求解某些复杂事件的概率时,可以把复杂事件分解为一些互斥事件的和,利用概率加法公式求解;也可以利用“正难则反”的思想,先求出复杂事件的对立事件的概率,再利用求解。

