执行器受限下离散网络控制系统容错控制
张 跞,刘冠邦,徐川川,李 荣,熊师洵
(1.中国电子科技集团 第二十八研究所,南京 210023;2.太原理工大学 电气与动力工程学院,太原 030000;3.南京邮电大学 物联网学院,南京 210003)
0 引言
在传统控制系统中,由于采用点对点的通信方式,一般具有布线复杂、维护成本高以及无法远程控制等缺点,因此,随着大规模工业化的兴起,传统的点对点控制系统已经不能满足工业化控制的要求。20世纪80年代以来,随着智能传感器技术、计算机技术以及网络通信技术的飞速发展,控制系统逐渐从点对点控制发展到基于计算机的分布式控制系统,直至通信网络出现并逐渐融入计算机控制系统,从而出现基于通讯网络的控制系统,即网络控制系统[1-4]。与传统点对点控制相比,网络控制系统具有可靠性高、灵活性强、资源共享等优点,且易于远程操作与控制[5-6]。因此,网络控制系统逐渐在工业、交通、医疗以及军事等领域得到了广泛的应用[7-8]。所以,作为控制论、信息论以及计算机通信技术的交叉融合产物,网络控制系统正逐渐从理论研究延申到越来越多的实际应用中。
从20世纪50年代开始,对于离散系统的有关研究,逐渐开始被控制学界所重视,并取得了众多的研究成果。一开始,人们对连续信号进行Z变换处理,随着计算机技术在工业生产和生活中的广泛应用,离散信号通过采样开关获取后被提供给微型计算机,计算机识别离散信号后再进行分析和处理,因此,对于计算机来说,离散信号是其唯一可以识别利用的信号。所以对于计算机控制系统来说,就算采集得到的信号是连续信号,也必须离散化为离散信号,再进行稳定性分析等处理。除了在计算机系统中得到应用外,离散系统也广泛存在于日常生活中,比如热线电话的排队系统,人口数据统计及红绿灯交通系统等。近些年来,随着计算机技术和控制系统的结合越来越紧密,离散网络控制系统的应用变得十分广泛。值得注意的是,在目前网络控制系统研究的浪潮下,对于连续的网络控制系统的研究相对成熟,而对于离散网络控制系统的研究则相对没有那么充分。
对于网络控制系统来说,通信网络的引入虽然给控制系统带来了诸多优点,但是由于网络的一些自身特性以及不同节点共享网络,通常会带来一些新的问题。
对于网络控制系统来说,传感器,控制器,执行器的节点在地理上往往分布较为广泛,同时由于网络带宽是有限的,会导致传感器,控制器和执行器在进行数据交换时数据碰撞、连接中断、网络阻塞、数据重发等现象,从而引起数据交换和传输出现延迟,这种由网络自身特性引起的时延被称为网络诱导时延。网络诱导时延往往由3个部分组成:传感器到控制器的传输时延,控制器到执行器的传输时延以及控制器的计算时延。相比之下,计算时延比传输时延和小很多,甚至可以忽略不记。此外,数据包容量、网络负载、网络传输速率等因素还会导致网络诱导时延发生改变,数据在网络传输的过程中时常受一些外界因素的干扰,例如随机的外部干扰等,这些都会导致时延发生改变。网络控制系统中存在不同特性的网络诱导时延,可能是随机的,可能是恒定的有,也可能是有界的,这主要取决于网络的通信协议。
网络控制系统在实际运行中,由于非理想网络特性和被控系统自身物理特性等限制,控制资源往往不能完全实时满足控制性能需求[9]。首先,执行器饱和是实际控制系统中常见的现象,当控制输入达到其物理极限时,称为执行器饱和,这种现象必然会给控制系统分析与设计带来困难[10]。例如:现代工业生产过程如石油、化工、冶金、制药、食品、钢铁等多个行业中,都需要监测和控制液位的高度,而实际的液位控制系统往往存在控制输入饱和受限问题,这将影响控制系统的性能,甚至导致系统失稳。其次,故障主要来源于系统长时间工作导致的组件老化、磨损以及系统维修时操作不当或错误操作等。故障信号会直接降低系统性能,甚至影响系统稳定性,其中执行器故障对系统性能影响最大[11]。执行器故障在不同工况下呈现的程度不一,例如:执行器部分失效、参数漂移、卡死、随机故障等,对控制系统分析和设计提出了巨大挑战。
从20世纪90年代开始,线性矩阵不等式逐渐被广泛应用于解决系统中的控制问题。随着内点法的提出,以及Matlab中的LMItoolbox的出现,线性矩阵不等式作为解决系统控制问题的一个重要工具,已经得到了越来越广泛地应用。线性矩阵不等式经过30多年的发展,广泛应用于时滞系统、不确定系统、切换系统等稳定性分析和控制器设计中。在此之前的Riccati方程法,有大量的参数和对称正定矩阵需要预先调整,而线性矩阵不等式方法不需要预先调整任何参数和正定对称矩阵,大大降低了问题求解的保守性。
因此,本文针对存在执行器受限(执行器故障/饱和)的离散网络控制系统,针对执行器故障和饱和受限分别进行建模,在充分考虑了时变网络诱导时延和系统参数不确定的情况下,系统的稳定性分析问题,并且设计了一类容错控制器,利用Lyapunov稳定性理论和LMI技术求解控制增益,使得闭环系统在设计的控制器作用下渐近稳定,最后,通过仿真验证了提出方法是有效的并具有更小的保守性。
符号说明:I代表单位矩阵,diag{·}表示对角矩阵,(*)表示对称矩阵的对称结构。AT表示其为A的转置矩阵,sym(A)表示A+AT;若A为非奇异矩阵,则它的逆矩阵表示为A-1。对于对称矩阵A,A>0(A<0)表示A是正定(负定)的。除特殊说明外,本文涉及到的矩阵均是适维矩阵。
1 问题描述
考虑一类带有系统参数不确定的离散时间系统被控对象如下:
(1)
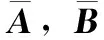
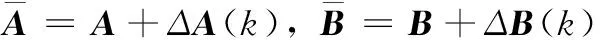
(2)
并且ΔA(k),ΔB(k)满足如下[13]:
(3)
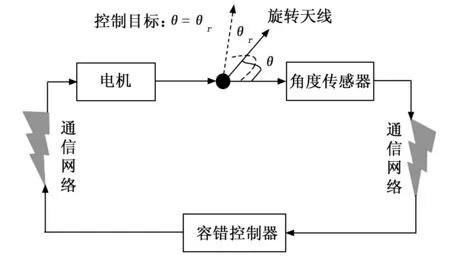
其中:D,E1,E2是已知常值矩阵,Δ(k)为时变矩阵且满足ΔT(k)Δ(k)≤I。控制结构框图如图1所示。
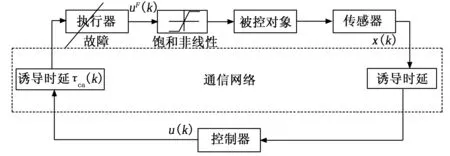
图1 网络控制系统结构框图
其中控制输入uF(k)收到饱和非线性的限制,可以表示为sat(uF(k)),其中sat(·)为饱和函数且有如下:
(4)
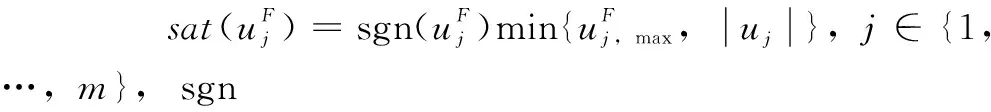

为了后文分析方便,给出如下假设条件:
假设1[14]:传感器系统采样信号数据为单包传输,且系统状态信息能够被测量。
假设2[15]:传感器是时间驱动的;控制器和执行器是事件驱动的。
假设3:为了分析方便,系统暂时不考虑传输丢包现象。
2 故障及饱和模型建模
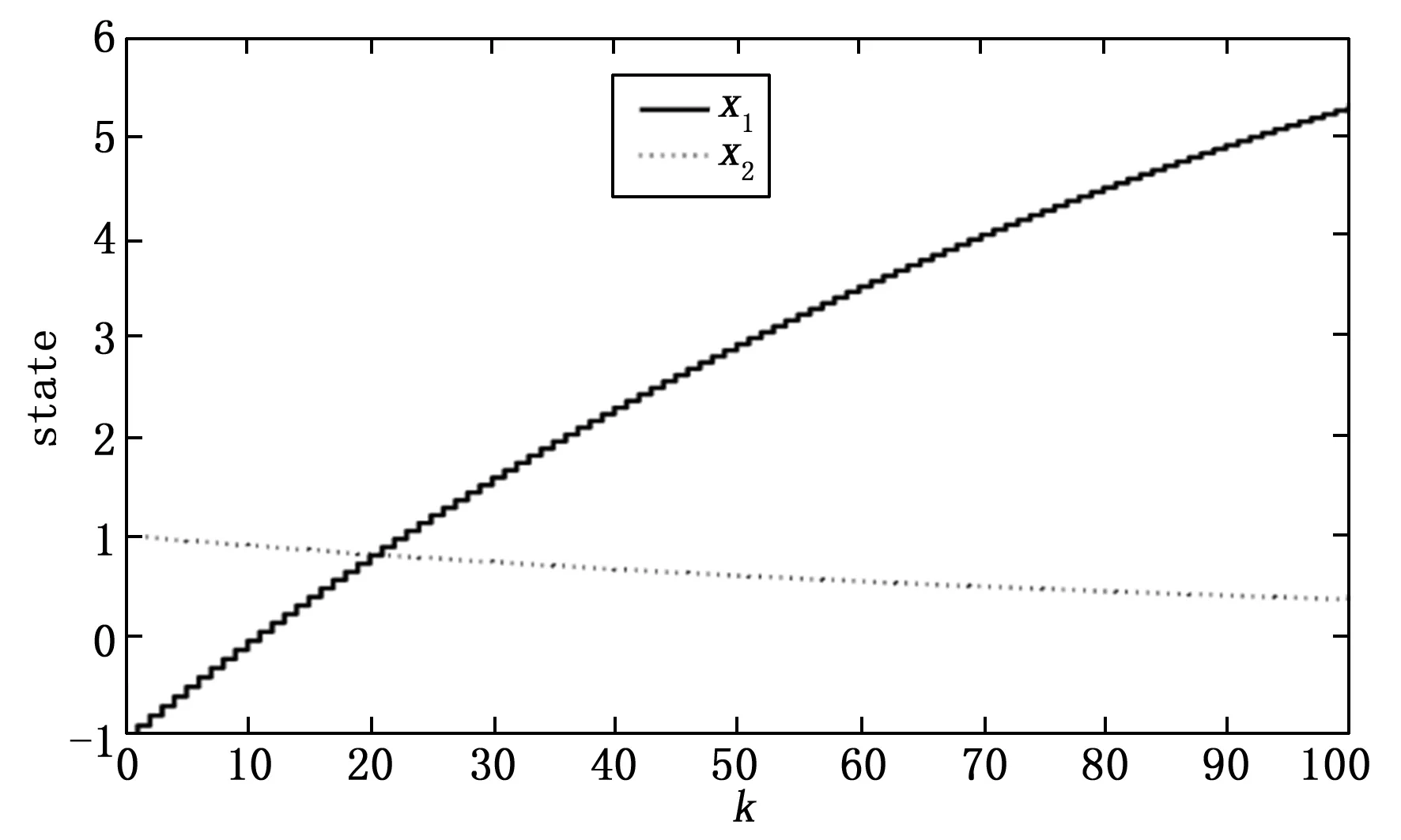
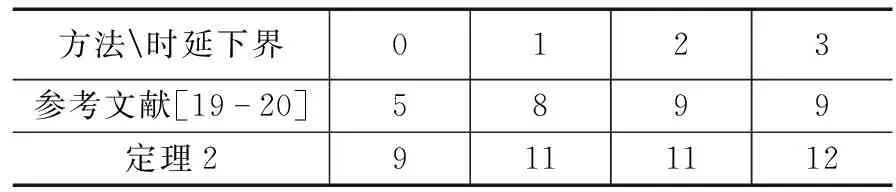
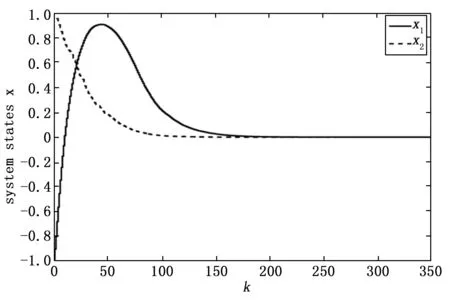
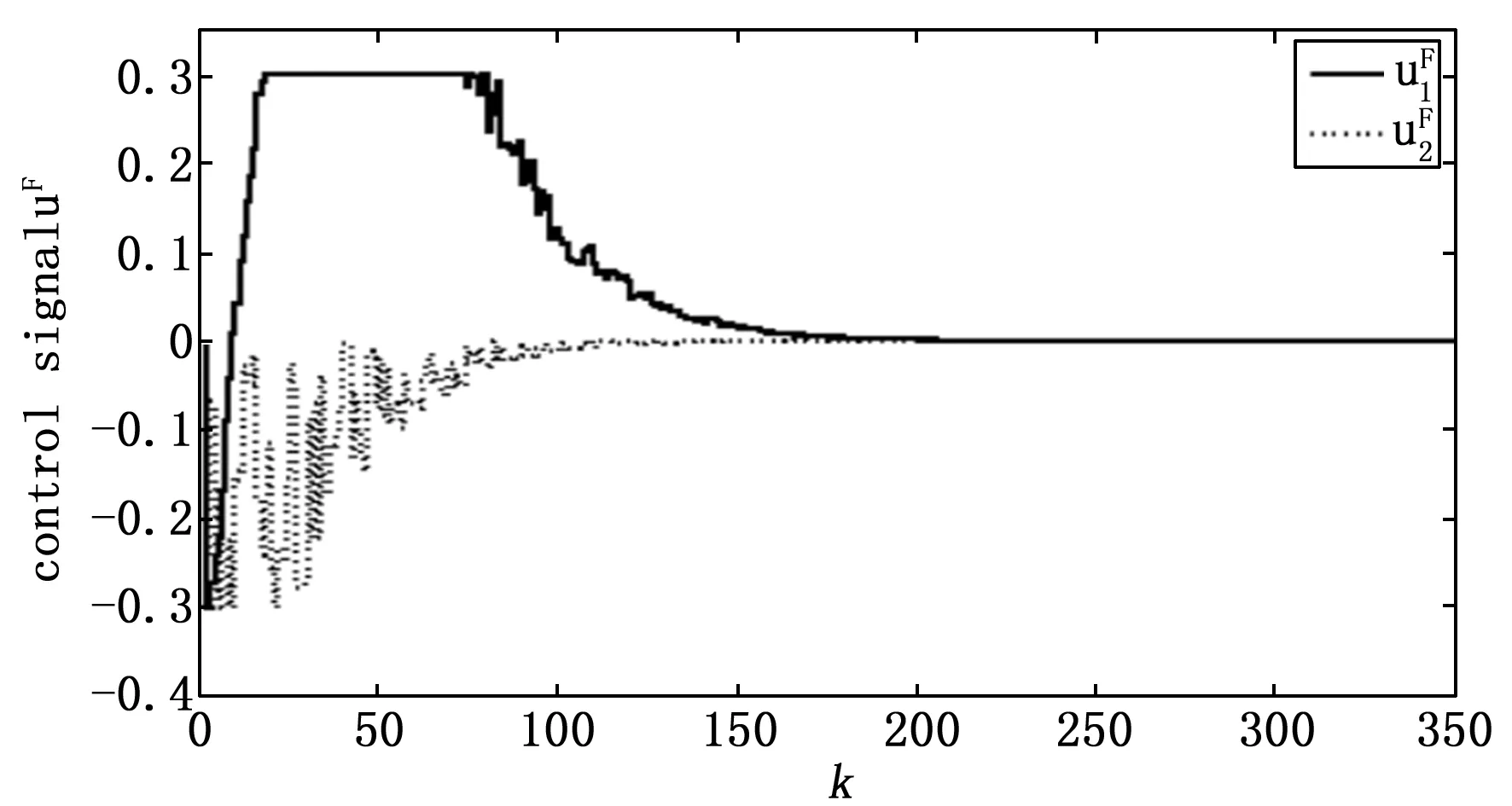
由于执行器存在故障,首先定义M(k)=diag{m1,m2,…,mm}为故障矩阵,其中mi=1(i=1,…,l)表示第i个执行器节点工作情况良好;mi=0,(i=1,…,l)表示第i个执行器节点存在全故障无法工作;0 mu=diag{mu1,…,mum},0 (5) ml为故障矩阵下界,可表示为: ml=diag{ml1,…,mlm},0 (6) 接下来定义矩阵: (7) (8) 根据式(8),可以得出|G(k)|≤I,其中|G(k)|=diag{|g1(k)|,…,|gm(k)|}。综合上面所述内容,M(k)可以等价为如下形式: M(k)=M0[I+G(k)] (9) 由于执行器同样存在饱和受限的现象,本文使用sat(uF(k))来表示执行器饱和受限,为了得到执行器饱和具体数学模型表达模式,给出了如下定义: 定义1[17-18]:如果非线性项Ψ(·)满足如下不等式: (Ψ(v)-H1v)T(Ψ(v)-H2v)≤0,∀v∈Rr (10) 其中:H1,H2∈Rr×r为实数矩阵且H=H2-H1。 H1为半正定矩阵,则称非线性项Ψ(·)满足[H1,H2]扇区限制条件。 根据文献[17]和[18],假设存在对角矩阵F1,F2且0≤F1≤I≤F2,因而饱和项sat(uF(k))可以表示为: sat(uF(k))=F1uF(k)+Ψ(uF(k)) (11) 其中:F1uF(k)为线性函数,Ψ(uF(k))为非线性项。根据定义1,如果设置H1=0和H2=F,则有: ΨT(uF(k))[Ψ(uF(k))-FuF(k)]≤0 (12) 其中:F=F2-F1。 接下来,针对上述存在执行器受限和执行器故障的离散网络控制系统进行控制器设计,得到闭环控制系统的稳定性分析结论,再基于LMI技术得到控制器增益的求解方案。 为了更好地得到后续结论,给出后文分析所需定义和引理。 定义1[12]:对于线性离散系统x(k+1)=f(x(k)),k=0,1,2,…且有f(0)=0,如果存在一个x(k)的变量函数V(x(k)),对所有的x(k)都满足: 1)V(x(k))>0 2)ΔV(x(k))<0,其中ΔV(x(k))=V(x(k+1))-V(x(k)) 那么平衡状态x=0是大范围渐近稳定的。 引理1[19]:(离散Jenson不等式)对于任意矩阵Z>0,正整数γ1>0,γ2>0满足γ2≥γ1≥1以及向量函数ω(·):[γ1,γ2]→Rn,则有如下不等式成立: 1)S<0; 引理3[20]:给定适当维数常数矩阵Γ,Λ与对称矩阵γ,对于任意满足FT(k)F(k)≤I的时变矩阵F(k),如果γ+ΓF(k)Λ+ΛTFT(k)ΓT<0成立,则对常数α>0,有如下不等式成立: γ+αΓΓT+α-1ΛTΛ<0 根据假设1,考虑传感器到执行器之间的网络诱导时延τsc(k),设计一类静态状态反馈控制器: u(k)=Kx(k-τsc(k)) (13) 其中:K∈Rm×n是需要待确定的控制器增益。考虑控制器到执行器通讯时延τca(k)以及执行器故障的影响,可以得到: uF(k)=M(k)u(k-τca(k)) (14) 根据式(13)和式(14),将τsc(k)和τca(k)组合成加性时延τ(k)=τsc(k)+τca(k),可以得到: uF(k)=M(k)u(k-τ(k)) (15) 根据式(11)和式(15),可以到如下闭环控制系统: (16) 首先,给出闭环系统(16)渐近稳定得成分条件。 为了后文分析方便,使用sym(A)代替A+AT。 定理1给出了闭环系统渐近稳定的条件。 (17) 其中: 则闭环控制系统(16)在控制器(13)作用下渐近稳定。 证明:记y(k)=x(k+1)-x(k),根据式(16),可以得到: (18) 接下来构造如下形式的Lyapunov-krasovskii泛函: V(k)=V1(k)+V2(k)+V3(k) (19) 其中: V1(k)=xT(k)Px(k) (20) (21) (22) 然后,基于闭环系统(16)对式(20)~(22)进行前向差分,可以分别得到: ΔV1(k)=2xT(k)Py(k)+yT(k)Py(k) (23) (24) (25) 针对式(25),利用引理1,可以得到: (26) 根据式(18),对于任意适当维数的常数矩阵L1,L2,L3则有如下恒等式成立: (27) 同时,基于式(12)和式(15),可以得到: (28) 定义增广向量ξ(k)为: ξT(k)= (29) 综合式(23)~(28),可以得到: ΔV(k)≤ξT(k)Πξ(k) (30) 根据式(17),可以得到ΔV(k)<0对任意ξ(k)≠0,根据Lyapunov稳定性定理,式(16)可以保证闭环系统渐近稳定,证明完毕。 注解1:定理1给出了判定闭环系统(16)渐近稳定的充分条件,但由于控制器增益K与其他未知矩阵耦合,同时由于存在参数不确定导致的时变未知矩阵,因此无法直接对控制增益K进行求解。下面,利用矩阵变换、不等式缩放、以及shur补引理等,建立基于LMI的控制器增益求解定理。 (31) 其中: 证明:根据式(9)和定理1中的结论,可以做如下形式的矩阵变换: (32) 其中: 而矩阵元素分别为如下所示: 由于GT(k)G(k)≤I,再根据引理1和引理3,如果存在正数α,使得如下不等式成立: (33) 其中相关矩阵元素分别为: 再根据式(1)和(3),Φ<0可以转化为如下形式: 其中:Φ可以表示为: 矩阵元素分别为如下: 接下来,根据引理3,可以知道存在 使得如下不等式成立: (34) 为了验证本文结论的有效性,选取文献[23]中的角度定位系统(angular position system)进行验证。角度定位系统如图2所示,由电机、角度传感器、控制器和旋转天线组成。 图2 角度定位系统示意图 被控对象状态空间模型如下所示: 同时,假设系统存在范数有界不确定: ΔA=DΔ(k)E1,ΔB=DΔ(k)E2 且有关参数分别为: 当u(k)=0时,开环系统状态响应曲线如图3所示,可以看出开环系统显然是不稳定的。 图3 开环系统状态响应曲线图 根据定理2,提前设定参数如下所示: 首先,为了说明本文提出方法可以降低结论的保守性,针对相同时延下的最大容许上界(MADB,maximun allowable delay bound)进行对比,从表1可以看出,使用定理2在不同时延下界下得到的最大容许上界均不低于使用参考文献[19-20]中的方法得到的最大容许上界,因此定理2得出的结论具有更小的保守性。 表1 不同时延下界下的MADB α=2.9547,λ=0.0392 因此可以得到控制器增益如下: 选取系统初始条件为xT(0)=[-1,1],在所设计的容错控制器(15)的作用下,闭环系统状态响应曲线和控制输入曲线分别如图4和图5所示。 图4 闭环系统状态响应曲线图 图5 控制输入信号曲线图 从图4和图5可以看出,被控系统虽然受到网络诱导时延、参数不确定、执行器饱和以及执行器故障等影响,控制输入始终受限在饱和幅值内,但所设计的容错控制器依然能让闭环系统保持渐近稳定,所以本文所得到的结论是有效的且具有更小的保守性。 在网络控制系统的实际应用中,由于工作环境的复杂性、外界干扰的存在以及自身节点物理特性的限制,系统的控制资源往往不能完全满足控制需求(执行器故障/饱和)。同时,由于通信网络的存在,网络诱导时延也是不可避免的。 本文针对离散时间网络控制系统存在网络诱导时延和系统参数不确定的情况,综合考虑了执行器饱和和执行器故障等控制资源受限的影响,研究了系统稳定性分析和控制器设计问题。将饱和项转化为一类存在扇形有界不确定性和非线性项,然后利用时延上界信息进行Lyapunov-krasovskii 泛函构造并利用离散Jenson不等式放大技术估计泛函差分更紧上界,再利用有关引理和矩阵不等式理论等将所获得的稳定性判据转化为容易求解的控制器增益求解方案,最后通过仿真验证比较,说明本章设计方法相较于现有相关文献具有更小的保守性,并且所设计的控制器在控制资源受限的情况下可以使得闭环系统保持稳定。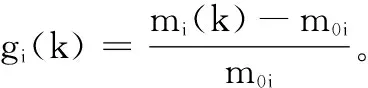
3 稳定性分析及控制器设计
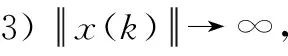
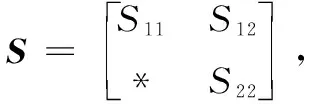
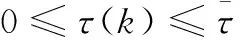
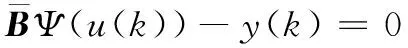
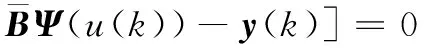
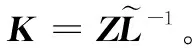
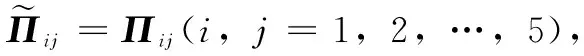
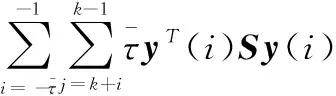
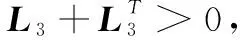
4 仿真验证
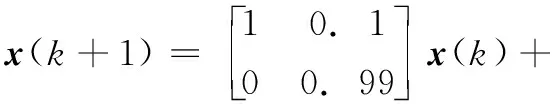

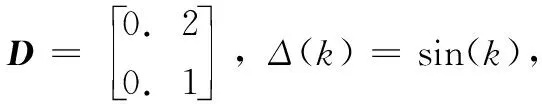
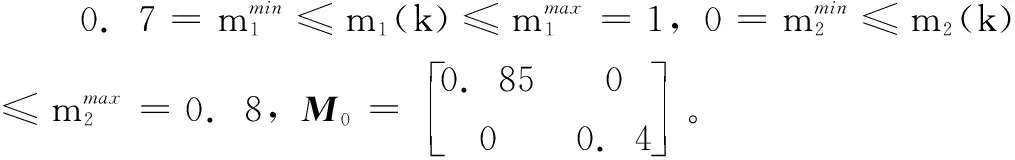
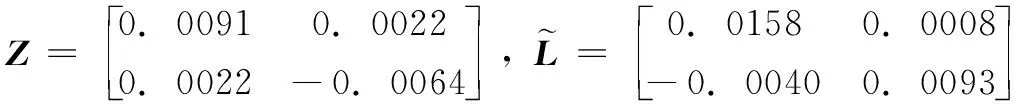

5 结束语

