空间向量在立体几何中的应用

■贵州省仁怀市周林高中 尹伟云

空间向量是高中数学的一个重要组成部分,在高考中具有较高的地位,是立体几何中的一个主要命题方向,往往以“证算并重”的方式进行考查。常以多面体为载体,考查用向量法确定空间点、线、面的位置关系,求解空间角、空间距离、立体几何中的动点探究性问题等。需要同学们借助向量的工具性作用,将空间几何量之间的位置关系转化为数量关系来求解。下面分类分析空间向量在立体几何中的应用。

1.证明共线与共面问题

例1如图1,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且|ED1|=2|DE|,|BF|=2|FB1|,线段EF的中点为M。

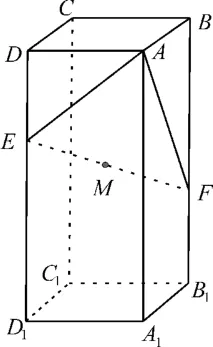
图1

求证:(1)点M在长方体的对角线AC1上;(2)点C1在平面AEF内。

由向量共面的充要条件知,点C1在平面AEF内。

评注:空间向量兼具代数与几何的双重特征,证明多点共线或多线共面问题也是从这两个方面入手,关键是掌握空间向量的线性运算法则和共线、共面的充要条件。

具体方法是:要证明三点共线,可以证明任意两点构成的一组向量共线且共点;要证明四点共面,可以利用向量共面的充要条件,即以其中一点A为起点,分别以另三点B,C,D为终点得到向量证明存在唯一的实数对(λ,μ),使成立即可;要证明两条直线共面,可以证明两条直线平行或相交,从而转化为两条直线的方向向量共不共线的问题,即若存在实数λ,使两条直线的方向向量a,b满足b=λa,则两条直线平行,若不存在实数λ满足b=λa,则两条直线相交。

2.证明线、面的平行与垂直关系

例2如图3所示,在直二面角D-ABE中,四边形ABCD是边长为2 的正方形,|AE|=|EB|,F为CE上的点,且BF⊥平面ACE,G为CE的中点。

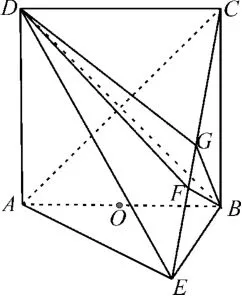
图3

求 证:(1)AE∥平 面BDG;(2)AE⊥平面BCE;(3)平面BDF⊥平面ABCD。

解析:因为ABCD为正方形,所以BC⊥AB。因为二面角D-AB-E为直二面角,平面DAB∩平面ABE=AB,所以BC⊥平面AEB。设线段AB的中点为O,连接OE。因为|AE|=|EB|,所以AB⊥OE。

评注:利用向量法证线面平行,一般有三个思路:一是用向量共面的充要条件,证明直线的方向向量能用平面内两条相交直线的方向向量表示出来,即这三个向量共面,根据共面向量概念和直线在平面外,得线面平行;二是先求出平面的法向量,再证明法向量与直线的方向向量垂直;三是证明已知直线与平面内的一条直线平行,也就是将其转化为证明线线平行的问题,再根据线面平行的判断定理得证。

证面面平行,一般有两个思路:一是利用向量证明一个平面内两条相交直线平行于另一个平面,根据面面平行的判定定理得证;二是求出两个平面的法向量,证明这两个法向量平行,则这两个平面平行。

证线线垂直,可转化为两条直线的方向向量垂直,即证明两条直线方向向量的数量积为0。

证线面垂直有两个思路:一是证平面的法向量与直线的方向向量平行;二是证直线与平面内两条相交直线垂直,再用线面垂直判定定理证明。

证面面垂直,先求出两个平面的法向量,通过证明这两个平面的法向量垂直即可。

以上思路大多要用到平面的法向量,当题中出现线面垂直时,则该直线的方向向量就是该平面的一个法向量,为减少计算量,无需另求法向量。

3.解决平行或垂直的探索性问题

例3如图5所示,在四棱柱ABCDA1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1 的正方形,侧棱|A1A|=2。

图5

(1)在棱A1B上是否存在一点M,使得A1D∥平面ACM?

(2)在棱A1A上是否存在一点P,使得平面AB1C1⊥平面PB1C1?

评注:涉及线段上的动点问题,先设出动点分线段的某个比值λ,根据两个向量共线的充要条件得数乘关系,从而用λ表示动点的坐标,再进行相关计算,这样可以减少未知量,简化过程。值得注意的是,应给出λ的取值范围。另外,建系时最好用右手直角坐标系且使几何元素尽量分布在坐标轴的正方向上。

4.求解点面距离或几何体的体积

例4如图7,在三棱柱ABC-A1B1C1中,棱AA1⊥侧面ABC,AB⊥BC,D为AC的中点,|AA1|=|AB|=2,|BC|=3,求三棱锥A1-BC1D的体积。

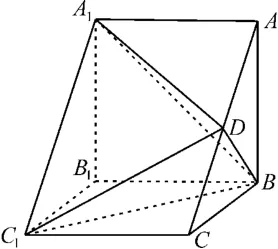
图7

解析:由题意知,B1C1,B1B,B1A1三条直线两两垂直,故以B1为坐标原点,建立空间直角坐标系B1-xyz,如图8所示。

5.求空间角

例5如图9,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,直线PA与底面ABCD成60°角,点N是PB的中点。

图9

(1)求异面直线DN与BC所成角的余弦值;(2)求直线PA与平面PBC所成角的正弦值;(3)求二面角P-NC-D的余弦值。

解二面角问题,是依据二面角两个半平面的法向量夹角与二面角相等或互补来处理。大多数情况下是根据图形判断该角是锐角还是钝角,有时也可以根据两个半平面的法向量的指向来判断。

6.结构不良型问题

例6(2022 年北京高考卷)如图11,在三棱柱ABC-A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,|AB|=|BC|=2,M,N分别为A1B1,AC的中点。

图11

(1)求证:MN∥平面BCC1B1。(2)再从条件①、条件②中选择一个作为已知条件,求直线AB与平面BMN所成角的正弦值。

条件①:AB⊥MN;条件②:|BM|=|MN|。

注:如果选择条件①和条件②分别解答,那么按第一个解答计分。

解析:(1)因为侧面CBB1C1为正方形,所以CB⊥BB1。又平面CBB1C1⊥平面ABB1A1,平面CBB1C1∩平面ABB1A1=BB1,CB⊂平 面CBB1C1,所以CB⊥平 面ABB1A1。

因为AB⊂平面ABB1A1,所以BC⊥AB。

评注:本题运用空间向量的三角形法则、平行四边形法则、数量积及模的运算,得到共面和垂直关系,避开了复杂的推理过程,无需添加辅助线,降低了思维难度,让人感到耳目一新。对于选择性条件的结构不良试题,应该选择一个易于入手的条件进行求解。

7.最值问题

例7(2022 年全国乙卷理数)如图13,在四面体A-BCD中,AD⊥CD,|AD|=|CD|,∠ADB=∠BDC,E为AC的中点。

图13

(1)证明:平面BED⊥平面ACD;(2)设|AB|=|BD|=2,∠ACB=60°,点F在棱BD上,当△AFC的面积最小时,求CF与平面ABD所成角的正弦值。

解析:(1)因为|AD|=|CD|,E为AC的中点,所以AC⊥DE。

又∠ADB=∠CDB,|DB|=|DB|,所以△ABD≌△CBD,|AB|=|CB|。连接BE,又因为E为AC的中点,所以AC⊥BE。

因为DE∩BE=E,所以AC⊥平 面BED。

因为AC⊂平面ACD,所以平面BED⊥平面ACD。

8.逆向探索性问题

例8已知四边形ABCD是梯形,S为AD的中点,BC∥AD,∠BCD=90°,|AD|=2|BC|=4。现将△ABS沿BS向上翻折,使A到A′,且二面角A′-BS-C为直二面角,E,F分别是A′S,A′B的中点,如图15所示。

图15

评注:对于距离、体积或空间角的逆向存在性问题,其求解思路是先假设条件存在,把假设当作新的已知条件进行推理,通过构造方程求解。若得到合理的数据,则假设成立;若出现矛盾,则假设不成立。对于翻折问题,关键是抓住翻折前后几何量的变与不变进行相关计算。