成对数据统计分析的五种考查方向

■西北师范大学附属中学 卢会玉

众所周知,独立性检验是统计学的一种检验方式,它是根据数据判断两类因子彼此相关或相互独立的假设检验。若要推断的论述为H1:“X与Y有关系”,可以利用独立性检验来考查两个变量是否有关系,并且能较精确地给出这种判断的可靠程度。具体的做法是,由表中的数据算出随机变量K2(即K的平方)的值,K2的值越大,说明“X与Y有关系”成立的可能性越大。独立性检验也是高考中的高频考点。若两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系。如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,这两个变量就具有线性相关关系。与线性相关有关的考查也是非常常见的。成对数据的统计分析,对同学们的数学建模、数学抽象、数据分析、数学运算等核心素养的提高,是非常具有意义的。

下文用几道例题对成对数据的统计分析进行盘点与分析。

方向一、成对数据的相关性

有时会借助散点图对成对数据进行分析,散点图中点的分布从左下角到右上角,两个变量正相关;点的分布从左上角到右下角,两个变量负相关。有时会借助样本相关系数对成对数据进行分析:当r＞0时,正相关;当r＜0时,负相关;|r|越接近于1,相关性越强。有时借助回归方程对成对数据进行分析:当＞0时,正相关;当＜0时,负相关。

例1某统计部门对四组数据进行统计分析后,获得如图1所示的散点图。

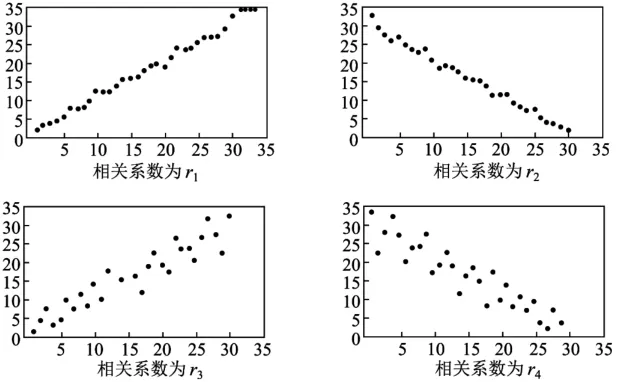
图1

下面关于相关系数的比较,说法正确的是( )。

A.r4＜r2＜r1＜r3

B.r2＜r4＜r1＜r3

C.r2＜r4＜r3＜r1

D.r4＜r2＜r3＜r1

解析:由图可知:r3,r1所对应的图中的散点呈现正相关,而且r1对应的相关性比r3对应的相关性要强,故0＜r3＜r1;r2,r4所对应的图中的散点呈现负相关,且根据散点的分布情况可知r2＜r4＜0。

因此,r2＜r4＜r3＜r1,选C。

例2对两个变量x,y进行线性相关检验,得线性相关系数r1=0.899 5,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是( )。

A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强

B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强

C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强

D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强

解析:依题意知r1=0.899 5,r2=-0.956 8,所以x,y正相关,u,v负相关。又|r1|＜|r2|＜1,故u,v的线性相关性较强,选C。

方向二、相关系数求解以及线性回归方程

例3重庆市位于北半球亚热带内陆地区,其气候特征恰如几句俗谚:春早气温不稳定,夏长酷热多伏旱,秋凉绵绵阴雨天,冬暖少雪云雾多。尤其是10月份,昼夜温差很大,某数学兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了2021年10月其中六天的昼夜温差情况与因患感冒而就诊的人数,得到资料(表1)。

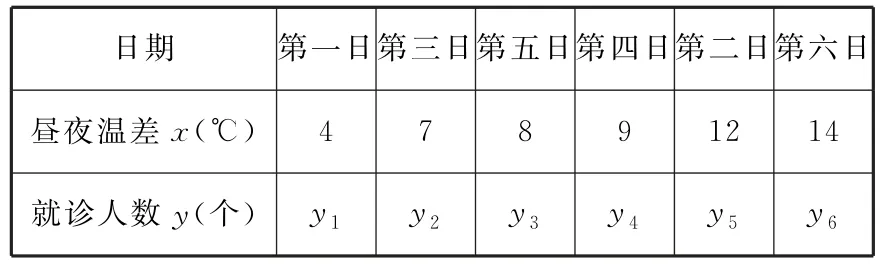
表1

(2)分析数据发现:第六日就诊人数y6=30,第一日就诊患者中有3个小孩,其他患者全是大人。现随机地从第一日所有就诊患者中选出2人,若2人中至少有1个小孩的概率为

①求y1的值;

②若y2＜y3＜y4＜y5,求y2,y3,y4,y5的值(只写结果,不写求解过程)。

例4某地经过多年的环境治理,已将荒山改造成了绿水青山。为估计一林区某种树木的总材积量,随机选取了10 棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如下数据(表2)。

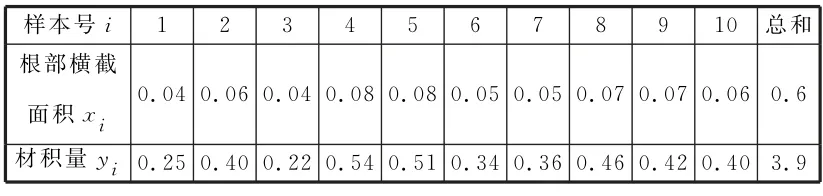
表2

(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量。

(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01)。

(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为186 m2。已知树木的材积量与其根部横截面积近似成正比,利用以上数据给出该林区这种树木的总材积量的估计值。

方向三、非线性回归方程

解决非线性回归问题的关键点是合理转化为线性回归问题,对运算能力的要求非常高。

例55G 网络是指第五代移动网络通信技术,它的主要特点是传输速度快,峰值传输速度可达每秒数十GB。作为新一代移动通信技术,它将要支持的设备远不止智能手机,而是会扩展到未来的智能家居、智能穿戴等设备。某科技创新公司基于领先技术的支持,经济收入在短期内逐月攀升,该公司1月份至6 月份的经济收入y(单位:万元)关于月份x的数据如表3所示,并根据数据绘制了如图2 所示的散点图。

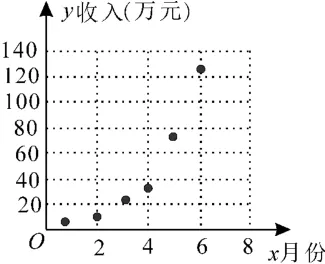
图2

表3

(1)根据散点图,判断y=ax+b与y=cedx(a,b,c,d均为常数)哪一个更适合作为经济收入y关于月份x的回归方程类型。(给出判断即可,不必说明理由)

(2)根据(1)的结果及表中数据,求出y关于x的回归方程。(结果保留两位小数)

(3)根据(2)所求得的回归方程,预测该公司7月份的经济收入。(结果保留两位小数)

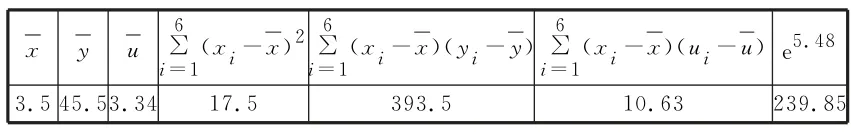
表4

其中u=lny,ui=lnyi(i=1,2,3,4,5,6)。

解析:(1)由散点图可知,y=cedx更适合作为经济收入y关于月份x的回归方程类型。

方向四、独立性检验

独立性检验不论是理解还是运算相对都要简单一些,正确解答的关键还是先理解题意后计算。

例62022 年北京冬奥组委发布的《北京2022年冬奥会和冬残奥会经济遗产报告(2022)》显示,北京冬奥会已签约45 家赞助企业,冬奥会赞助成为一项跨度时间较长的营销方式。为了解该45 家赞助企业每天销售额与每天线上销售时间之间的相关关系,某平台对45 家赞助企业进行跟踪调查,其中每天线上销售时间不少于8小时的企业有20家,余下的企业中,每天的销售额不足30万元的企业占统计后得到如下2×2列联表(表5)。

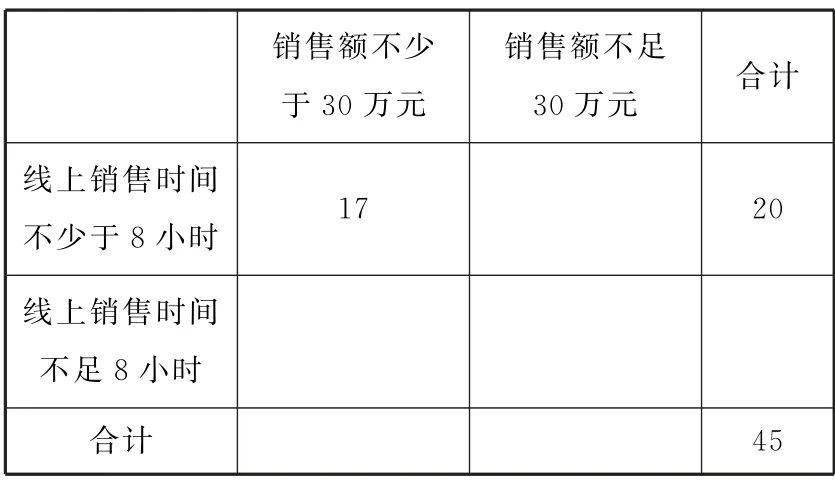
表5

(1)请完成上面的2×2 列联表,能否有99%的把握认为赞助企业每天的销售额与每天线上销售时间有关?

(2)按销售额在上述赞助企业中采用分层抽样方法抽取5家企业,在销售额不足30万元的企业中抽取时,记“抽到线上销售时间不少于8小时的企业数”为X,求X的分布列和数学期望。

附:

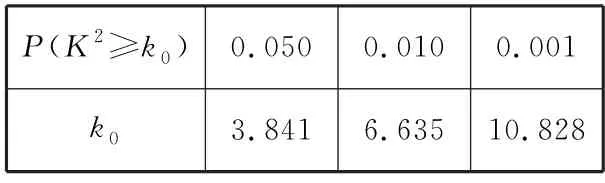
表6

参考公式:

解析:(1)由题意,可得下面的2×2列联表(表7)。

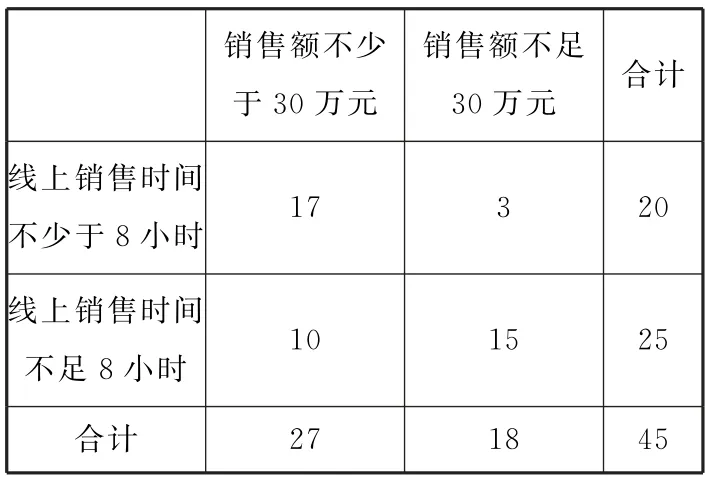
表7

根据上面的列联表得:

故有99%的把握认为赞助企业每天的销售额与每天的线上销售时间有关。

所以随机变量X的分布列如表8所示。

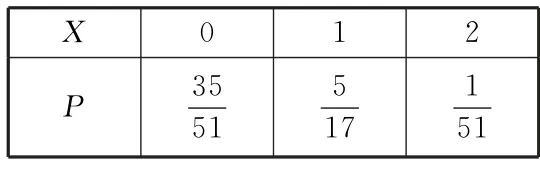
表8

方向五、成对数据的综合考查

例7共享汽车,是指许多人合用一辆车,即开车人对车辆只有使用权,而没有所有权,有点类似于在租车行业里的短时间租车。它手续简便,打个电话或通过网上就可以预约订车。某市为了了解不同年龄的人对共享汽车的使用体验,随机选取了100名使用共享汽车的体验者,让他们根据体验效果进行评分。

临界值表(表9)。

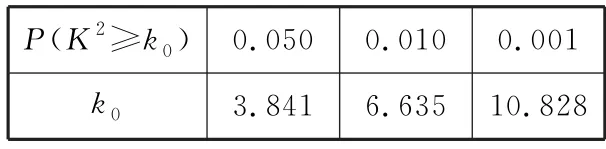
表9

(2)现将100名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请将列联表(表10)补充完整并判断是否有99.9%的把握认为对共享汽车的评价与年龄有关。

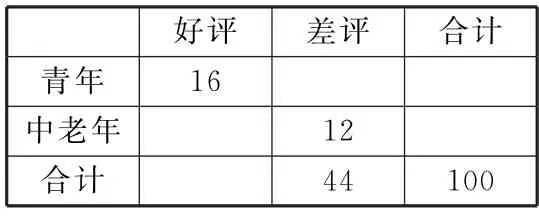
表10

因为0.9＞0.75,所以可以判断对共享汽车使用体验的评分与年龄的相关性很强。

(2)根据题意可得列联表(表11)。

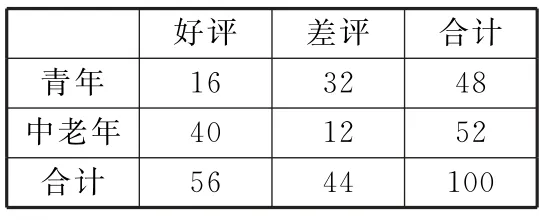
表11

解得:

成对数据的统计分析是高考考查的高频考点,如果每一种考查方向的关键点是明晰的,运算也是精准的,那对于同学们来说就会比较顺利。另一方面,成对数据的统计分析,对同学们的终身发展也是非常有意义的。