多智能体强化学习博弈训练方式研究综述

张人文,赖 俊,陈希亮

(陆军工程大学 指挥控制工程学院,江苏 南京 210007)

0 引 言

近年来,强化学习(Reinforcement Learning)[1]逐渐成为人工智能的热门研究领域。智能体(Agent)通过采取不同的动作(Action)与环境进行交互[2],改变自身状态(State),并获得奖励(Reward)。通过引导智能体获得更大收益的方式驱使智能体进行学习,完成任务。2017年,以强化学习算法为核心的AlphaGo战胜围棋世界冠军李世石,引发人们的广泛关注。随着研究深入,更符合现实需求的多智能体强化学习(Multi-agent Reinforcement Learning)获得人们重视,已在决策支持、智能推荐、即时战略游戏等领域取得进展。

博弈训练方式的运用为强化学习技术进一步赋能。采用种群训练的“FTW agent”[3]在《雷神之锤III竞技场》中达到人类玩家水平;采用联盟训练的AlphaStar[4]在《星际2》中战胜人类顶尖玩家;采用自我博弈训练的OpenAI Five[5]在《Dota 2》中战胜世界冠军,在即时战略游戏中击败世界冠军。

该文对多智能体强化学习基本理论、博弈基本理论、多智能体强化学习博弈训练方式分类、关键问题和前景展望进行综述。其中第二节对强化学习基本理论、博弈基本理论进行简要阐述;第三节结合多智能体博弈训练研究成果应用对典型博弈训练算法进行分类及介绍;第四节分析博弈训练的关键问题及挑战;第五节简要介绍现有部分多智能体强化学习博弈训练平台;最后对多智能体强化学习博弈训练的发展前景及展望进行讨论。

1 基本理论

本节对强化学习及博弈论的概念进行阐述,介绍博弈求解方式发展历程及博弈训练的基本含义。

1.1 强化学习基本理论

1.1.1 马尔可夫决策过程(MDP)

MDP由多元组构成,一般包括S,A,P,R,γ等,S表示智能体状态空间,A表示智能体动作空间,P为智能体状态转移函数, 其定义为[6]:

P:S×A×S→[0,1]

(1)

P代表智能体在状态s∈S的情况下,采用给定动作a∈A时,状态转移至下一状态s'∈S的概率分布。智能体的瞬时回报函数R为:

R:S×A×S→R

(2)

R表示智能体在状态s的情况下,采用动作a时,状态转移至下一状态s'所获得的即时回报。将所有即时回报累加,可得到智能体的总收益Rt:

(3)

式中,γ∈[0,1]是折扣系数,用于平衡智能体的瞬时回报和长期回报对总回报的影响[7]。

马尔可夫决策过程中,当智能体从一个状态转移到另一状态时,只需要考虑当前的状态与行为,不需要考虑以往所采取的行为以及所处的环境[8]。

1.1.2 强化学习

强化学习是智能体通过与环境交互以期获得最大收益而采取的学习方式。智能体通过采取最优的动作与环境进行交互,获得回报,进而学习到指导问题解决的最佳策略。通俗而言,强化学习即智能体在环境中不断“试错”,以最大化回报为驱动力,在试错过程中逐渐适应环境,达成学习的目的。

智能体与环境的交互过程可以由三个要素来描述:状态s、动作a、奖励r。智能体根据初始状态s,执行动作a并与环境进行交互,获得奖励r,转移至下一状态s'[9]。强化学习基本过程如图1所示。

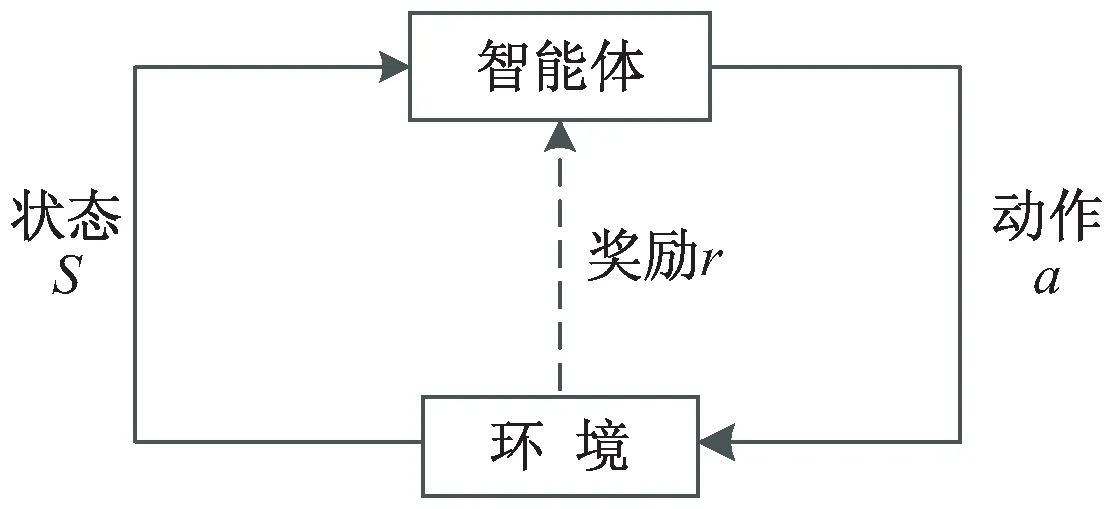
图1 强化学习基本过程

智能体学习成果是获得一个适合环境的策略π,π是智能体可能会选择某种行为的概率[8],表示为:

π:S×A→[0,1]

(4)

策略可分为确定性策略和随机性策略。确定性策略即智能体在不同时刻(t)或回合(episode)时,遇到相同状态均选择某一确定的动作。随机性策略为一个概率分布,即为智能体输入一个状态,输出选择某个动作的概率。随机性策略可表示为:

π(a|s)=p(at=a|st=s)

(5)

在智能体与环境交互的过程中,不断优化其目前使用的策略,使策略越来越好,这个过程即策略更新。策略更新在强化学习中迭代执行,以期智能体能得到一个最佳策略。为了判断智能体在某一状态s时策略的优劣,定义状态值函数Vπ(s):

Vπ(s)=E[Gt|st=s,π]

(6)

同样,为了判断智能体在某一状态s时执行动作a的优劣,定义状态动作值函数Qπ(s,a):

Qπ(s,a)=E[Gt|st=s,at=a,π]

(7)

其中,Gt是智能体从当前状态一直到交互过程结束所获得的总收益R,即累计回报。

在强化学习过程中,智能体通过对值函数进行评价,进而判定自身策略优劣并加以改进。

1.2 多智能体强化学习

现实场景往往有多个主体交互,多智能体系统(Multi-Agent System,MAS)[10]是对现实世界多主体交互场景进行的一种建模方式。多智能体强化学习(Multi-Agent Reinforcement Learning,MARL)[11]是采用强化学习方法对多智能体系统进行训练的人工智能方法,遵循随机博弈(Stochastic Game,SG)[12]过程。

在多智能体强化学习中,智能体的动作空间Ai(i=1,2,…,n)交互形成联合动作空间A:

A=A1×A2×…×An

(8)

策略、状态转移函数等也相应改变。如联合状态转移函数,即全部智能体在执行联合状态动作a时,由状态s转移至下一状态s'的概率分布。智能体的联合策略决定智能体的总回报。

多智能体强化学习算法可分为完全合作型、完全竞争型和混合型[13],采用多智能体强化学习能完成复杂任务,提升算法效率[6]。

1.3 博弈论

博弈论(Game Theory)[14]是对存在利益关系的理性行为实体之间的冲突或合作模型进行形式化研究的一门学科[15]。博弈论的形式化表述一般由玩家(Player)、策略(Strategy)、收益(Payoff)、理性(Rationality)等要素构成。

博弈论有多种分类。根据博弈过程玩家是否同时决策,可分为标准式博弈(静态博弈)、拓展式博弈(动态博弈);根据玩家对博弈过程信息是否了解,可分为完美信息博弈和不完美信息博弈等。

对于一般标准式博弈,进行如下形式化定义:

(9)

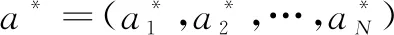
a-i=(a1,…,ai-1,ai+1,…,an)

(10)

根据理性假设,每名玩家在博弈中都试图通过寻求针对其他玩家的最优响应(Best Response)来获得更高收益。若当每名玩家均采用最优响应时,任何一方单独改变策略都不能使自己获得更高的收益,此时博弈达到一种稳定的局面,即纳什均衡(Nash Equilibrium)。

纳什均衡是博弈论的重要理论基础,纳什证明了标准式博弈中均衡点的存在[16],为博弈论的应用开创了理论基础。其形式化定义如下:

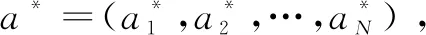
(11)

1.4 博弈求解方式的发展历程

纳什均衡提出后,求解纳什均衡成为研究的热点。自我博弈的使用在精神上类似于虚拟博弈[5]。

1951年,Brown[17]提出虚拟博弈(Fictitious Play,FP)的概念。Genugten[18]提出弱化形式的虚拟游戏(Weakened Fictitious Play,WFP),获得近似最优响应,加快收敛速度。Heinrich[19]提出Full-width extensive-form fictitious play(XSP)和Fictitious Self-Play(FSP),将虚拟博弈由标准式博弈推广到扩展式博弈。Heinrich等人[20]提出Neural Fictitious Self-Play (NFSP),是第一个在自我博弈中收敛到近似纳什均衡的深度强化学习方法。另一方面,McMahan等人[21]提出基于博弈论的Double Oracle(DO)算法,在此基础上,Lanctot等人[22]提出Policy Space Response Oracles (PSRO)算法,提升了博弈求解水平。Balduzzi 等人[23]提出PSRO-rectified Nash response(PSRO-rN),进一步提升了纳什均衡下策略的改进机率。Muller等人[24]提出α-PSRO算法,使用α-Rank[25]扩展PSRO的理论基础,避免求解纳什均衡面临的均衡选择问题[26]。McAleer等人[27]提出Pipeline PSRO(P2SRO),通过维护分层管道来并行化 PSRO。

1.5 博弈训练

博弈训练,是在对抗性环境中,智能体通过和当前的自己及自身历史版本进行博弈对抗的训练方式。一方面,如何在数据不足或有限的情况下,训练出符合要求的智能体,需要寻找一种能够平衡训练数据规模与智能体训练效果的方法。另一方面,如何在复杂场景中训练智能体获得更优的策略,突破策略循环,博弈训练开辟了一个新的途径。

2 博弈训练方式分类

根据基础原理的不同,可将博弈训练分为基于自我博弈的训练和基于博弈论的训练;根据从对手策略池中不同“挑选和应对对手”方法,基于自我博弈的训练又可划分为自我博弈、种群训练和联盟训练。

2.1 自我博弈训练

自我博弈(Self-Play,SP)是在多智能体训练的背景下出现的一种训练方案[28]。自我博弈训练的本质是通过自身行为模拟产生数据,并利用数据进行学习和提升[29]。自我博弈的实证成功挑战了经典观点,即专家对手是获得良好表现所必需的[30]。

Samuel[31]在跳棋程序中设计了自我对战,发现这种模式早期特别好。Epstein[32]指出,自我博弈训练的程序有条不紊地确定和探索自己在搜索空间中的路径。Tesauro等人[33]设计了TD-Gammon,在玩西洋双陆棋的能力上达到专家水平。在训练AlphaGo[34]的策略网络时,将当前正在训练的策略网络Pρ和从对手池中随机抽样的对手Pρ-进行对弈。AlphaGo Zero[35]的训练数据全部来自于自我博弈训练。Kaplanis等人[36]指出,每个智能体的经验分布会受到对手不断变化的策略影响。Balduzzi等人[23]描述了自我博弈训练算法,指出自我博弈适合由传递博弈建模的游戏。Hernandez 等人[28]使用形式符号定义了SP的通用框架,在该框架下统一了流行的SP算法的定义,进一步指出自我博弈表现出周期性的策略演变[37]。

2.1.1 自我博弈训练算法基本框架

Balduzzi等人[23]描述了一种自我博弈训练算法。其中oracle表示,从上帝视角,oracle能够找到一个智能体Vt',其能力比Vt更好。该定义描述,通过自我博弈训练,Vt+1的能力均比Vt要好,如算法1描述:

算法1 Self-Play算法。

输入:智能体V1

对t=1,2,…,T执行以下循环:

智能体Vt+1←oracle(智能体Vt',φvt(·))

结束循环

输出:智能体VT+1

Hernandez等人[37]定义了通用的自我博弈训练框架,描述了所有自我博弈训练方案的最小结构,同时未对策略交互的环境做出任何假设。

πο:πο∈ai;表示策略集(menagerie),智能体的行为从策略集中进行采样,集合包括当前的训练策略π,并随着训练的进行而不断改变。

Ω:Ω∈[0,1];表示策略抽样分布(policy sampling distribution),即策略集πο上的概率分布。

G:G∈[0,1];表示门控函数(gating function),决定是否将当前策略π引入策略集,及哪些策略π∈πο将丢弃,如算法2描述:

算法 2:强化学习Self-Play算法。

输入:环境等要素(S,A,O,P,R等);

输入:Self-Play要素(Ω,G);

输入:需要训练的策略π。

1 初始化策略集πο={π};

2 对e=0,1,2…执行以下循环:

3 根据策略抽样分布Ω从πο中抽取π';

4 将π'加入π中;

5 采样S0和O0;

6 对t=0,1,2…,直至终止,执行以下循环:

7 根据策略π及观察Ot选择动作并执行;

8 结合状态St和动作at,根据P得到St+1和Ot+1;

9 获得奖励rt;

10t=t+1;

11 结束循环;

12 更新π;

13 根据G决定是否将当前策略π加入策略集πο

14 结束循环

15 输出策略π

2.1.2 经典自我博弈训练算法

经典自我博弈训练算法(Naive Self-Play,NSP)是最典型的自我博弈训练算法,1959年Samuel在其论文中已经使用[31],智能体每次都与最新版本的自己进行对战,即智能体均在相同的最新策略的指导下进行交互[37]。形式化表述如下:

(12)

此时,门控函数G总是将最新版本的策略放入策略集πο中,且策略集中仅保持最新策略[37]。

G(π°,π)={π}

(13)

Samuel[31]使用经典自我博弈方法训练跳棋游戏,发现这种模式在训练早期阶段效果较好。Kaplanis等人[36]通过仅针对自身最新版本的自我博弈训练,来评估智能体的持续学习能力。通过将最终智能体与在训练的各个阶段的模型进行对比,发现智能体的能力得到了平稳的提高。但也发现存在少数被击败的情况。

2.1.3 成长式自我博弈训练算法

成长式自我博弈训练(Mature Self-Play,MSP)的核心是与过去的自我对战。即训练时将训练过程中产生的模型收集起来,加入到模型池(对手池)中,正在训练的智能体不仅与最新版本的自我对战,还采用多种抽样方式与过去版本的模型进行博弈对战。

Bansal等人[38]发现,智能体针对最新版本的自我进行博弈训练会导致训练不平衡。相反,针对随机旧版本对手的训练效果要好,可以获得更强大的策略。

根据博弈训练时新旧模型不同采样比例及不同采样方式,可分为多种算法:

(1)历史均匀训练法。

History Uniform Self-Play(HUSP)。即智能体在进行博弈训练时,以在整个历史版本上进行均匀随机采样选择对手,使用Uniform(0,v)方法,其中v是抽样时的模型版本总数。参考Hernandez等人[37]描述的自我博弈训练框架,将HUSP方法形式化描述如下:

Ω(π'|π°,π)=Uniform(0,M)

(14)

门控函数G采用确定性策略吸收新的策略。每次训练后,将当前策略加入到策略集中。

G(π°,π)=π°∪{π}

(15)

Al-Shedivat等人[39]在进行模型的预训练时,将模型自我博弈过程中的历史版本进行保存,用于后期的对抗训练。Silver等人[34]在训练AlphoGO的策略网络时,使用当前策略网络和随机选择的先前策略网络进行博弈对战,不断增强对手池的多样性。

(2)区间均匀训练法。

区间均匀法是Bansal等人[38]提出的考虑对手抽样时新旧版本占比的方法,目的是训练出能够击败自身随机旧版本的策略。即选取对手时,不是在整个历史版本上进行均匀随机采样,而是使用Uniform(δM,M)方法,其中M是抽样时对手池内所含模型版本数量。δ∈[0,1]是抽样比例的阈值。Hernandez等人[37]将该方法命名为δ-Uniform Self-Play(δ-USP),形式化描述为:

Ω(π'|π°,π)=Uniform(δM,M)

(16)

与历史均匀训练法相同,门控函数G为:

G(π°,π)=π°∪{π}

(17)

Bansal等人[38]发现,针对最新版本的对手进行自我博弈训练会导致最差的表现。δ的取值对不同的场景较为敏感,将直接影响博弈训练效果。

(3)区间限制训练法。

受到RL方法顺序数据收集方式影响,较早的对手比最近添加的对手被更加频繁地采样。Van Der Ree[40]发现,训练期间对手策略质量与智能体策略的潜在质量呈现相关性。相对而言,早期智能体版本的性能较差,可能影响智能体最终训练效果。

Hernandez等人[37]提出了一种新的博弈训练方法,命名为δ-Limit Uniform Self-Play(δ-LUSP)。通过改进对手抽样分布,定义了新的采样概率公式和归一化算法,增加后续策略被抽样的概率。

(18)

(19)

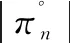
Hernandez等人[37]发现这种方法能够降低早期版本的抽样频率,但仍然存在策略循环的情况。

(4)回溯比例训练法。

回溯比例训练法是前述方法的结合,博弈训练时,以一定训练比例与最新的自我对战,其余训练比例与过去的版本对战。回溯比例训练法未舍弃任何过去的对手,所有历史对手均保存在对手池中。

该文给出回溯比例训练法的形式化描述:

(20)

lastestself表示与最新版本模型进行对战,即经典自我博弈;historyself表示与过去版本对手模型进行对战,可根据需求选择多种对手抽样算法;η∈[0,1]表示lastestself在总体训练中所占比例。

表1 典型自我博弈训练方法分类

OpenAI Five进行自我博弈训练时,80%的训练场次采用经典自我博弈法,20%的训练场次与过去的对手进行对战,即η=0.8。Berner等人[5]指出,保持与过去的版本进行对抗,获得更强大策略的同时,减小智能体忘记如何打败过去对手的可能性。

Inseok等人[41]使用了类似方式,但以概率p选择最近的k个版本对手,以1-p的概率选择其余版本,p以一定的方式下降,前期较大的p有助于快速适应对手,后期使用较小的p减轻灾难性遗忘的影响,稳定学习过程[41]。

2.2 种群训练

PBT(Population Based Training)算法[42]具有高效和易并行的特点,进化策略类似于遗传算法[43]。

图2 常见的参数调优方式

For The Win(FTW)[3]采用基于种群的自我博弈训练算法(Population Based Training Self-Play,PBTSF),将PBT算法与多智能体强化学习方法结合。智能体之间的关系是多样的,根据训练效果“优胜劣汰”,获得水平较高的智能体并保持鲁棒性。

种群内的每个智能体使用Elo分数[44]作为标准,抽样与其水平相近的对手,使对战结果具有不确定性,当智能体胜率低于70%时,将较好智能体的参数复制至较差智能体,同时对参数进行探索[3],这种方式思想上类似遗传算法的选择、交叉和变异阶段。

PBTSF使整个种群内的智能体相互对战,每个智能体都要进行学习,通过挑选高水平智能体并不断进行探索,使整个种群都变得更加智能。

2.3 联盟训练

由于策略循环非传递性问题的限制,自我博弈训练常常会陷入局部最优中,无法获得更好的表现。

Vinyals等人[4]为名为AlphaStar的星际争霸AI设计了一种新的博弈训练算法——联盟训练(League Training),旨在解决自我博弈训练中常见的循环问题,并整合各种策略[4]。对手抽样方面,Vinyals等人[4]设计了优先虚拟自我博弈算法(Prioritized Fictitious Self-Play,PFSP),PFSP使用了新的抽样匹配机制:

(21)

上式含义为:给定一个正在训练的智能体A,从对手池C中采样对手B的概率为p。式中,f:[0,1]→[0,∞)是权重函数,Vinyals等人[4]设计了fhard(x)和fvar(x)两种具体的函数:

fhard(x)=(1-x)2

(22)

fvar(x)=x(1-x)

(23)

fhard(x)是PFSP的默认式,智能体专注于较难战胜的对手。为了避免陷入只与最难对手对战的循环,PFSP还提出另外一种形式fvar(x),使智能体关注与自己水平相近的对手。

联盟由三种不同类型的智能体组成,包括主智能体(Main agents)、主利用者(Main exploiters)和联盟利用者(League exploiters)[4]。主智能体是最终需要的智能体,采用混合策略进行对手采样,且不会被重置。主利用者的目标是发现主智能体的缺陷。打败智能体了解的对手是不够的,培养更好的对手也很重要,他们表现出智能体不知道的行为[23]。联盟利用者的目标是发现整个联盟的弱点,使用PFSP在联盟中抽样对手进行训练,采用一定的规则被重置。

星际争霸指挥官(StarCraft Commander,SCC)[45]也采用了联盟训练方法。Wang等人[45]设计了智能体分支(Agent branching),使用当前主智能体初始化新的主利用者,而不使用监督学习的参数。Han等人[46]设计了TStarBot-X,采用多元化联盟训练(Diversified League Training ,DLT),丰富了联盟的多样性。

2.4 策略空间响应预言机

基于博弈论的博弈训练方面,Lanctot等人[22]定义了策略空间响应预言机(Policy Space Response Oracle,PSRO)算法,统一了多智能体训练的博弈论算法。

PSRO算法是双预言机(Double Oracle,DO)算法[21]的延伸,是基于博弈论的博弈训练方式,通过迭代生成相对于现有策略单调更强的策略解决博弈训练问题。DO算法根据对手历史策略求出纳什均衡,采取最优响应,若当前最优响应已在策略空间中,则算法终止,否则将此最优响应作为新的策略加入策略空间,继续迭代至终止[47]。

图3 Double Oracle算法示意图

PSRO算法迭代进行以下循环:在当前策略集上定义元博弈(meta-game),通过使用元求解器获得元博弈最优响应,每个博弈训练轮次加入新的策略(通过“Oracle”获得),近似最优响应不断提升。开始时仅有单个策略[22],最终得到近似最优响应。

与DO算法操作的“动作”不同,PSRO算法的操作对象是“策略”,不同的元求解器以及从元求解器生成新策略的过程是PSRO算法之间的区别所在。

PSRO具有泛化性明显的特点,但强化学习训练可能需要很长时间才能收敛到近似最优反应。Lanctot等人[22]提出深层认知层次(Deep Cognitive Hierarchies,DCH)算法,提升训练速度,但牺牲了部分准确性。Balduzzi等人[23]提出改进版本PSROrN(Response to the rectified Nash),鼓励智能体“放大自的优势并忽略自身的弱点”。Muller等人[24]提出α-PSRO算法,使用α-Rank[25]扩展PSRO的理论基础,避免求解纳什均衡的均衡选择问题[26],在扑克中得到更快收敛的实例[24]McAleer等人[27]提出Pipeline PSRO (P2SRO),通过维护分层管道来并行化PSRO,同时具有收敛保证。Smith等人[48]提出两种PSRO变体,减少应用深度强化学习所需的训练量。

3 博弈训练的关键问题与挑战

3.1 策略循环

在具备博弈对抗性质的现实场景中,多智能体强化学习可能会遇到传递性场景和非传递性场景。以游戏场景为例,传递性游戏[23]可以通过等级或积分的高低判断胜率;而诸如石头剪刀布等非传递性游戏[23]则极有可能表现出策略循环,为博弈训练带来挑战。

自我博弈对于传递性游戏有较好策略提升效果。Balduzzi等人[23]指出,自我博弈是一种开放式学习算法,具有传递性。然而,对于非传递性游戏,智能体的一个策略改进并不能保证针对其他策略均改进。

为了跳出非传递性场景中的策略循环,许多研究者利用游戏环境进行了尝试。OpenAI Five采用并行自我博弈生成训练数据,确保智能体对广泛的对手具有鲁棒性。联盟训练[4]采用不同类型的智能体组合,在解决策略循环问题上取得了一定进展。SCC[45]和TStarBot-X[46]对联盟训练进行了丰富和探索。Balduzzi等人[23]提出PSROrN算法,为应对策略循环挑战提供了新的思路。

3.2 策略遗忘

在多智能体强化学习博弈训练过程中,训练后期的模型对战前期版本的模型时胜率下降,甚至被前期版本击败,这种策略遗忘的情况广泛存在。

由于利用神经网络学习新任务时,需要更新相关参数,但前期任务提取出来的知识也储存在这些参数上,因此学习新任务时,智能体会遗忘旧知识。Fedus等人[49]建立了灾难性遗忘与强化学习中样本效率低下等核心问题的经验联系。Reed等人[50]构建了多任务智能体 Gato,在更高层次解决策略遗忘问题。

3.3 策略探索

探索(Exploration)是强化学习的一个关键挑战,其目的是确保智能体的行为不会过早收敛到局部最优[51]。通过博弈训练得到的模型,是否可以在真实的博弈环境中发挥很好的效果,取决于当前智能体所在的环境分布与真实分布之间的差距情况。

Epstein[32]指出,在自我博弈训练中,不能保证智能体探索的空间是最重要的部分,并且探索的区域可能与所需要的几乎无关。Tesauro等人[33]指出,在确定性博弈环境中,通过自我博弈训练的系统最终可能只探索状态空间非常狭窄的部分。Inseok等人[41]指出,自我博弈得到的策略空间并不能保证对具有较大问题空间的场景具有足够覆盖率。

为了应对探索难题,许多研究者进行了深入的探讨。Pathak等人[52]提出好奇心探索(Curiosity-driven Exploration)算法,使智能体能够进一步探索环境并学习有用的策略。Fortunato等人[53]提出NoisyNet算法,帮助智能体进行有效探索。Ecoffet等人[54]提出Go-Explore 算法,记录访问状态,提升了探索效率。

3.4 策略突破

如何在策略提升的过程中突破策略循环,是一个重要挑战。首先,对于剪刀石头布这样完全循环的博弈场景而言,哪个策略更好是没有实际意义的。其次,策略的探索和遗忘在一定程度上制约高质量策略的获得,同时受算法、硬件条件限制,存在现实困难。Czarnecki等人[55]分析了现实世界游戏的几何特性,指出现实世界的游戏是由传递部分和非传递部分混合而成,几何结构类似于旋转陀螺。

目前,研究者从设置规则、添加人类经验、利用人类玩家数据等方面进行了有益尝试。AlphaGO使用人类专家数据进行监督学习,而后通过自我博弈训练进行改进提升。AlphaStar[4]和SCC[45]在监督学习中利用高质量人类数据集进行初始化,在强化学习中利用联盟训练方式提升和改进智能体。JueWu[56]虽没有使用人类数据用于智能体初始化,但其将人类高质量数据用于分析英雄阵容。OpenAI Five[5]未直接使用人类数据,但在神经网络和奖励函数等设计中一定程度上融入了人类先验知识。

4 博弈训练测试框架及平台

4.1 MALib

MALib[57]是首个专门面向基于种群的多智能体强化学习的开源大规模并行训练框架(官网链接:https://malib.io/)。支持自我博弈、联盟训练及PSRO等多种博弈训练方式,已对接多种多智能体环境。

4.2 POAC

部分可观测异步智能体协同(POAC)平台[58]是多智能体强化学习算法的标准测试环境(官网链接:http://turingai.ia.ac.cn/app/detail/30),可用于兵棋AI人机对抗挑战,支持自我博弈、人机对抗等模式。

4.3 Go-Bigger

Go-Bigger是OpenDILab推出的多智能体强化学习博弈训练环境(文档链接:https://gobigger.readthedocs.io/en/latest/index.html),涵盖自我博弈、联盟训练等多种博弈训练方式,提供了直观、高效的平台。

4.4 RoboSumo

RoboSumo[39]是多智能体竞争环境,具有模拟物理特征,使用相扑规则,智能体观察敌我位置、速度等参数,在连续动作空间进行自我博弈训练。

5 博弈训练的前景展望

博弈训练方法为多智能体强化学习开拓了思路,解决现实场景的能力有了显著提升,必将成为未来博弈训练的重点研究方向。同时,博弈训练方法还存在一些亟待解决的问题。

一方面,目前的博弈训练方法大多是启发式的[59],具体的理论解释还不完善,如新旧版本的比例设定、抽样方式的设计,可解释性不强,泛化性较弱。

另一方面,正如通过博弈训练能否获得最强玩家一样,智能体的决策水平能否通过自身博弈无限地提升下去?智能体自我博弈学习是否存在极限[29]?从这两个方面来看,博弈训练方法的研究还处于起步阶段,需要进行更加深入细致的研究。

6 结束语

从智能体训练的角度出发,对多智能体强化学习博弈训练方法进行了梳理,介绍了博弈训练的基本概念、方式分类、关键问题、测试平台及前景展望等。通过该文可以看出,多智能体强化学习博弈训练是一种新兴的智能体训练方式,能够在许多现实复杂场景中获得较好表现,具有极大的发展潜力和应用价值。相信随着研究的深入,博弈训练必将不断在可解释性、解决策略循环、探索、突破等问题上取得进展,成为多智能体强化学习领域一颗闪亮的新星。