无控靶弹发射运动特性与设计分析

何 鹏，刘晓濛，王浩宇，郝义龙，王燕宾，孙福合

(上海航天动力技术研究所，上海 201108)

0 引言

靶弹能够模拟来袭导弹的外形尺寸、运动特性、红外辐射特性、微波反射特性以及对抗特性等,其使用贯穿于防空武器系统科研试验和应用的始终。高性能靶弹系统已经成为试验鉴定部门考核防空武器系统不可或缺的装备[1]。在靶弹发展过程中,始终存在着“好用”和“用得起”之间的根本矛盾,一方面,随着现代防御技术的快速发展,对靶弹技术水平提出了越来越高的要求;另一方面,由于靶弹是非作战装备,且属于一次性使用的消耗品,靶弹开发投入的人力和财力资源有限[2]。无控靶弹舍弃了弹上诸多控制设备,结构简单,是目前低成本靶标的一种。

无控靶弹需配合发射装置进行倾斜式定向发射。定向支承方式是影响发射初始扰动的重要因素,直接影响弹道散布[3],其设计合理与否直接关系到靶标任务的成败。弹体从定向装置上滑离的方式主要有非同时离轨、同时离轨和瞬时离轨3种。非同时离轨设计结构相对简单,但前定向件离轨后,弹体会产生低头力矩,使弹体绕后定向件下沉转动;同时离轨设计虽然没有低头力矩干扰,但是结构相对复杂,弹架设计、制造、维护成本也因此会增加许多;瞬时离轨的发射导向性差,不利于无控弹发射。对于讲究低成本的无控靶弹,工程上一般采用非同时离轨设计。

起始扰动[4]是对靶弹飞行散布偏差影响较大的主要因素之一,它是靶弹离架瞬间,弹架相互作用影响造成[5]。无控靶弹由于没有控制设备,发射后无法对飞行弹道纠偏,靶弹离轨时的状态参数就显得更为重要了。同时针对发射离轨运动特征进行弹架配合设计,避免靶弹与发射架滑轨非必要的擦刮,提高发射离轨过程的稳定性。

1 低成本无控靶弹设计

为开发一款低成本靶弹,导弹与靶弹发射阵地选取试验场已有平台,节省了阵地建设开销。同时靶弹发动机、发射架、发控设备等均采用已有产品进行选配,发射形式为倾斜、非同时离轨。基于弹道相似性条件,参考某型火箭弹进行靶弹缩比设计与气动仿真[6-7],减少设计与研制成本。以已有发动机结构为基础,搭配头锥、曳光舱、尾舱与弹翼等就可组成简易的低成本靶弹,如图1所示。曳光舱用于提供导弹跟踪的红外特征信号,发动机提供初始推力,其他结构件则用于提供外弹道所需的气动外形。

图1 简易靶弹结构组成Fig.1 Simple composition of the target projectile

与导弹不同,靶弹弹道并非以“快、准、狠”为目的,而是以在特定飞行空间内保持指定飞行状态为设计原则,满足导弹试训所需。指定飞行状态指的是导弹攻击时需要靶弹达到一定范围的高度、速度与弹道倾角等运动状态。满足这些所有因素“与”集的飞行状态,才能满足导弹打靶的需求。特定飞行空间主要指的是根据导弹发射阵地与靶弹发射阵地之间的布局,指定靶弹被攻击时的空间区域。尤其对于采用已有的发射试验阵地而言,靶弹弹道需要优先配合导弹的发射窗口,否则即使靶弹可以飞出指定的飞行状态,但由于此时空间上不适应导弹试训需求(迎攻或尾追等),那也不为所用。同时还要考虑靶弹落点应在试验场允许区域等。

无控靶弹由于无控制系统,其飞行姿态与稳定性它全依赖自身结构设计与弹架配合保证。而弹重、转动惯量、推力、发射角,轨道长度等,对靶弹离轨与弹道均有耦合影响,不同的参数搭配都有可能导致弹速、射高等过大或过小。通过调整靶弹设计参数进行靶弹弹道试算,并配合导弹试训的交汇弹道确定靶弹弹道。

设计前期为了尽快完成导弹与靶弹交汇弹道计算迭代,一般不考虑靶弹离轨过程[8]。但这忽略了靶弹非同时离轨工况给后续弹道计算带来的影响,后期设计可针对无控靶弹非同时离轨的工况对飞行弹道计算进行修正,进一步提高靶弹外弹道计算精准度。

2 靶弹非同时离轨运动数值仿真模型

当靶弹发动机点火后,靶弹在发动机推力、重力、摩擦力与滑轨约束力等作用下沿滑轨飞出。从靶弹启动至完全脱离滑轨,靶弹运动过程可分为2个阶段:1)双定向滑块在轨运动,靶弹在2个定向滑块支撑下沿滑轨向前滑动,直至前定向滑块离轨瞬间;2)单(后)定向滑块在轨运动,前定向滑块离轨后,靶弹仅在一个支撑点作用下(即后定向滑块)沿滑轨向前滑动,在重力、推力的作用下,靶弹将绕支撑点产生一小幅度的低头运动,直至后定向滑块离轨[9-10]。

为了研究问题的需要,在此作如下假设:1)将靶弹与发射架滑轨视为理想刚体,即无弯曲与扭转变形;2)不考虑发射架和靶弹的振动;3)在固定地面上发射靶弹;4)不考虑风的影响;5)由于滑块尺寸相对于弹长与滑轨长度来说很小,视前滑块、后滑块为理想支点;6)考虑推力偏心影响[11]。如图2,建立靶弹离轨过程中的坐标系Oxyz,取待发射时后滑块(支点)与滑轨的接触点为坐标原点O;Ox轴沿滑轨方向,发射方向为正;为y轴垂直于滑轨方向(即Ox轴),向上为正;Ox轴与Oy轴包含铅锤面内,Ox轴按右手定则确定。另外,l1为靶弹前滑块支点到滑轨顶点距离,l2为靶弹前、后滑块支点之间的距离,C为靶弹质心,θ0为滑轨与水平面之间的夹角,即发射角。

图2 坐标系设置Fig.2 Coordinate system

1)双定向滑块在轨运动,即x≤l1时:

(1)

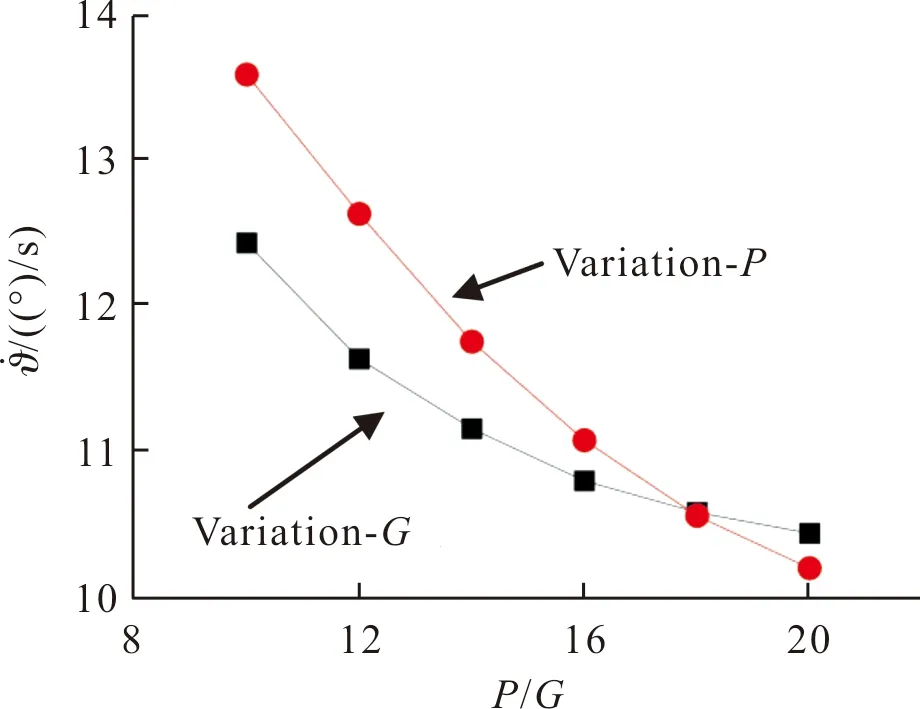
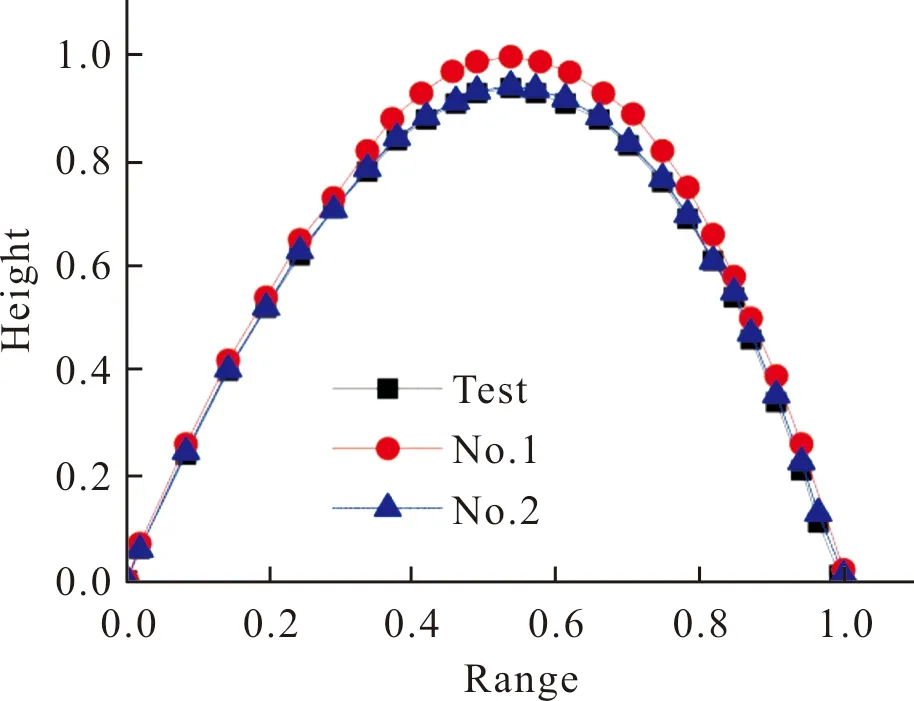
2)后定向滑块在轨运动,即l1

(2)

由式(1)、式(2)可知,靶弹离轨状态(速度、时间、转动角度、转动角速度)与弹重、转动惯量、发射角等参数有关。在一定推力条件下,调节弹体重量会同时影响靶弹推重比与转动惯量,两者对靶弹离轨的转动角速度有相反的影响,再结合发射角度,这些参数又会对无控靶弹外弹道具有直接影响,因此在设计无控靶弹结构时,需结合离轨运动计算与外弹道计算耦合考虑。

3 靶弹离轨运动特性分析

图3 前滑块离轨时间Fig.3 Derailment time of the front-slider

图4 前滑块离轨速度Fig.4 Derailment velocity of the front-slider

图5 后滑块离轨时间Fig.5 Derailment time of the rear-slider

图6 后滑块离轨速度Fig.6 Derailment velocity of the rear-slider

图7 弹体离轨转动角度Fig.7 Rotation angle when the target is out of orbit

图8 弹体离轨转动角速度Fig.8 Rotation angular velocity when the target is out of orbit

由图3～图6可知,相同发射角情况下,推重比越大则前、后滑块离轨时间越短,速度也越快,且影响程度明显:推重比由10增长20时,前、后滑块离轨时间缩短约28%,离轨速度提高约42.5%左右。

相同推重比情况下,发射角越大,则前、后滑块离轨时间越大,离轨速度越小,但这种影响程度很小:发射角由25°变化至60°,前、后滑块离轨时间延长仅约1.6%,离轨速度降低仅约1.3%。因此在无控靶弹设计时,推重比是调整离轨时间与速度的主要手段,但发射角调整则更多的应从外弹道设计方面考虑。

由图7、图8可知,提高发射角与推重比,对降低靶弹离轨瞬间的低头角度与低头角速度影响程度均较大。相同推重比(10～20)情况下,发射角由25°变化至60°,低头角度与角速度降低约43%、44%;相同发射角(25°～60°)情况下,推重比由10增长至20时,低头角度降低约42%,而低头角速度降低约16.5%。

由式(2)可知提高转动惯量可降低靶弹低头角速度。但根据图8的计算结果,在一定推力的条件下,增加重量可以提高转动惯量,最终却增加靶弹低头角速度。为说明该问题,这里假设靶弹重量、结构不变,即转动惯量不变,通过其他手段(药量、比冲等)调整平均推力达到推重比变化(不计药量变化重量),35°发射角度情况下靶弹低头角速度理论计算结果如图9所示,可知在保持结构重量的情况下(转动惯量不变),调整推重比(即推力)对低头转动速度影响相比更大,说明增大转动惯量虽然对减小低头转动速度有一定作用,但影响程度不及推重比。但这是针对本型靶弹中药量占弹重比例较小的情况,对于药量占比大的靶弹,推重比、转动惯量对离轨时的低头角速度影响程度要另外计算比较。

图9 发射角度35°时弹体离轨转动角速度Fig.9 Rotation angular velocity of the target off orbit when the firing angle is 35°

4 弹架运动干涉分析

由于靶弹离轨低头转动,靶弹与滑轨发生擦刮情况的地方有两处:1)在后滑块后端处。后滑块随弹体发生转动,若沿y向的位移大于滑块与滑轨之间的设计间隙,就会发生剧烈擦刮[12],增大对滑轨磨损程度,降低发射架有效使用寿命;2)在滑轨前端面处。靶弹会绕后滑块支点发生转动,在滑轨最前端位置(x=l1+l2)处弹体沿y向的下沉位移若大于弹体下表面距滑轨上表面的设计间隙,就会发生弹架擦刮,降低发射架架体稳定性,从而影响靶弹离轨的方位精度。

后滑块因靶弹离轨低头转动而产生沿y向的位移h1为:

h1=lh·sin ϑ

(3)

式中:lh为后滑块长度。

靶弹在滑轨前端面处沿y向的下沉位移h2为:

(4)

式中:L为滑轨长度;r为后滑块支点到弹轴的距离。

某型靶弹发射角为32°,推重比15,根据式(1)、式(2)计算得:靶弹前滑块离轨时间0.224 s,此时靶弹速度为30.307 m/s,此后靶弹开始以后滑块为支点继续滑行,并伴随低头转动,且角速度逐渐增大;0.254 s后,靶弹后滑块离轨,此时靶弹速度为34.991 m/s,低头转动角速度12.131°/s,最大转动角度为0.178°。

再联立式(3)～式(4),计算得出某型靶弹滑轨过程中后滑块垂直位移h1与靶弹在滑轨前端处垂直下沉位移h2的变化,见图10、图11。0.224 s前,靶弹前滑块未离开轨道,h1、h2为0。0.224 s后,前滑块离轨,h1随ϑ增大而单调上升,最大值为0.16 mm,考虑制造公差,滑块与滑轨设计间隙为0.4 mm,确保靶弹完全离轨前,后滑块不会因为靶弹转动而产生额外的接触应力;h2先逐渐增大,0.246 s时达到最大,最大值为0.46 mm,随后逐渐减小至0,整个过程ϑ逐渐增大,但支点(即后滑块)距导轨前端面距离,即(L-x)逐渐缩短。考虑制造公差,靶弹下表面距滑轨上表面距离设计间隙为3 mm,确保了离轨过程中不会导致靶弹与滑轨前端面有擦刮问题而影响发射稳定性。

图10 靶弹滑轨过程中h1变化Fig.10 Change in h1when the target is moving in orbit

图11 靶弹滑轨过程中h2变化Fig.11 Change in h2when the target is moving in orbit

5 靶弹弹道计算修正与分析

考虑靶弹非同时离轨运动影响,对无控靶弹弹道求解进行修正,本质上是对外弹道方程组数值求解中的计算参数初始赋值进行修正,而修正值由非同时离轨运动方程组求解得出。为此将靶弹从启动到落地的运动过程分为两部分串联计算:第一部分为非同时离轨运动方程组;第二部分为典型的外弹道方程组[13],由于篇幅原因,外弹道方程组不再冗述。

为实现串联计算,在非同时离轨运动方程组设定一个变量,用于适时的中止非同时离轨运动方程计算,转而继续执行外弹道方程组求解。这里设定的变量是后滑块运动距离x,当在离轨运动中x>(l1+l2)时,表征靶弹已离轨结束,根据计算结束步的各计算参数换算出靶弹离轨时刻、速度、质心相对位置、弹体俯仰角、弹体俯仰角速度等参数,为外弹道方程组初始计算参数赋值,最后完成外弹道计算。

表1 外弹道初始计算参数赋值情况Table 1 Initial value in calculation of ballistics

图12～图13为该型靶弹的2组计算工况的弹道仿真(高度—射程、速度—时间)结果与弹道实测曲线对比,数据进行了归一化处理。表2为两组仿真结果对实测数据在弹道平飞段(弹道倾角±15°)高度与速度的计算误差。

图12 靶弹归一化射程与高度曲线Fig.12 Range and height of the target(normalization)

图13 靶弹归一化飞行速度与时间曲线Fig.13 Flying speed of the target(normalization)

表2 弹道平飞段飞行速度与高度对比Table 2 Comparison of altitude in level flight

第二组采用离轨修正算法后对无控靶弹平飞段的飞行速度影响不大,但对飞行高度影响较大,且更吻合实测弹道。因此对于采用非同时离轨方式的无控靶弹,有必要考虑离轨运动对其后续弹道的修正。

6 结论

对无控靶弹非同时离轨发射工况进行研究,主要结论如下:

1)因前、后滑块非同时离轨会导致靶弹离轨过程中产生低头角度与角速度,这对于后续无控靶弹飞行弹道计算是不可忽视的修正因素。

2)发射角主要影响靶弹离轨角度与角速度,对离轨速度与时间影响较小,同时推重比对它们影响均较大。

3)靶弹滑块与发射架滑轨配合设计时应校核靶弹离轨过程中的弹体位移,避免弹架擦刮现象,降低发射架磨损程度,提高无控靶弹发射稳定性。

4)弹架干涉分析中假设靶弹与发射架滑轨为理想刚体,实际工程设计中靶弹与导轨配合设计应考虑一定结构变形量与生产制造偏差。