两栖战车海上行进间发射动力学研究

卢志伟，刘馨心，麻小明，胡建国，黄阳阳

(西安现代控制技术研究所，陕西 西安 710065)

0 引言

导弹发射技术随着科学技术的发展、作战使用的需求和导弹性能的改进而不断发展变化。传统的两栖战车受海浪波动影响,携带的武器无法在海上浮渡时实现高精度射击,若要实现行进间射击,其精度将受一定影响。行进间发射可以实现战车在水上行驶过程中完成对于导弹发射的准备过程,保证在第一时间对敌方进行火力打击。不同于静止水面,海浪的激励是一个随机激励,因此求得导弹发射的初始扰动分布情况对于导弹的设计和发射情况的判断至关重要。

对于两栖战车在海上行进间发射问题的研究,国内外学者[1-8]较多采用计算流体软件进行仿真,分别得到了两栖车的航行特性、航行姿态等参数,但并未对车载导弹的发射初始扰动进行研究;除了CFD计算,还采用了数值求解的方法,刘云等[9]用数值方法对行驶阻力进行了分析;居乃鵕[10]采用合理的假设,并根据动量定理和动量矩定理建立了某型战车海上运动方程,以及在随机海浪中行进的数值求解方法;麻小明等[11]在文献[10]基础上得出了战车的安全性和稳定性;余浩等[12]得出了航向角对于初始扰动影响规律。

文中基于数值分析的方法,将两栖战车在四级海况中行进间发射的模型进行简化,利用动力学仿真软件得到车上导弹在不同射角下发射的初始扰动,通过统计学计算得到导弹初始扰动的分布情况,采用正交实验设计的极差分析法判断导弹在两栖车上发射角度对于导弹发射初始扰动的影响。

1 车辆水上动力学方程

1.1 模型假设

基于两栖战车特性和海浪特性,进行如下假设:

1)随机海浪可以看成是正态平稳随机过程,是由无数个不同波长、波幅且沿着同一个方向传播的微幅余弦波叠加而成,这些波的初相位是一个随机变量;

2)两栖战车及其武器系统看做是质量特性和物理特性一定的刚体,不考虑变形对仿真带来的影响;

3)武器系统所受的力和力矩可简化为作用在系统质心的力和力矩,且因单发导弹的质量与武器系统相比可忽略不计,因此不考虑导弹发射过程中武器系统质心变化;

4)导弹所受风载荷对发射过程的影响可忽略不计。

以上假设可以在保证仿真准确性的前提下减少数据计算,提高计算效率。

1.2 坐标系描述

根据船舶通用的ITTC坐标系,结合车辆研究习惯,建立车辆随车坐标系,将车辆视为一个在水面上作六自由度运动的刚体,在车辆的质心处建立OXYZ坐标系,纵轴OX在其纵剖面内且平行于车体基线,正向指向车首; 横轴OY平行于车体基面,正向指向左侧;OZ轴垂直向上;同时简化车辆和导弹模型,如图1所示。

图1 车辆模型示意图Fig.1 Schematic diagram of vehicle model

两栖战车沿着坐标系中X,Y,Z轴的线位移x,y,z,线速度为u,v,w;绕着3个坐标轴转动的角位移为φ,θ,ψ,角速度为p,q,r。

1.3 车体受力分析

两栖战车在海上行进间发射受到的力和力矩主要有[12]:恢复力与恢复力矩Rk、附加质量惯性力与力矩Rm、阻尼力与力矩Rn、推力与力矩Rt、其他水动力与力矩Ra与Rb、操纵控制力与力矩Rc、导弹射击力Rg与力矩和海浪干扰力与力矩Rs。

将上述的力和力矩结合,得到两栖战车在海上行进间发射的外力和外力矩:

R=-Rk-Rm-Rn-Ra-Rb+Rt+Rc+Rg+Rs

(1)

1)恢复力和恢复力矩

在车辆的六自由度运动中,航行、侧滑和航向3个方向运动一般不存在恢复力和恢复力矩,而垂向、横摇和纵摇3个方向运动,当初始z0,φ0值和θ0不是运动的平衡位置时,存在着恢复力和恢复力矩,可使车辆从z0,φ0和θ0回到平衡位置。Rk可表示为:

Rk=(0,0,Zk,Kk,Mk,0)T

(2)

式中,Zk,Kk,Mk分别为车辆垂向、纵摇、横摇方向恢复力矩。

而Kk,Zk,Mk可表示为:

(3)

式中,kφ,kz,kθ分别为横摇、垂向和纵摇方向弹性系数。

2)附加质量惯性力和惯性力矩

Rm可表示为:

(4)

3)阻尼力和阻尼力矩

Rn可表示为:

(5)

式中n为阻尼特性参数。

4)推力和推力力矩

Rt可表示为:

Rt=(Xt,0,0,0,0,0)T

(6)

由航行特性分析可得:

Xt=T0-txu

(7)

式中:Xt为牵引力的大小;T0为拖桩牵引力;tx为推力速降系数。

5)操纵力和控制力矩

Rc可表示为:

Rc=(0,0,0,0,0,Nc)T

(8)

由航行特性分析可得:

Nc=(1-β)(nrT0-nrtxu)

(9)

式中:β为水门开度;nrT0,nrtx为考虑推力特性参量T0和tx的反喷操纵结构系数。

6)导弹发射干扰力和干扰力矩

导弹的发射力由试验测得作用在弹的尾部,相应的产生方向相反、大小相同的后坐力作用在发射箱上。

7)海浪干扰力和干扰力矩

车辆在海浪的作用下将做各种复杂的摇荡运动,若仅研究海浪对车辆横摇、纵摇和垂向运动的激励干扰过程,则海浪干扰力和干扰力矩向量中考虑垂向扰动力Zs、横摇扰动力矩Ks和纵摇扰动力矩Ms,即在随车坐标系中有:

Rs=(0,0,Zs,Ks,Ms,0)T

(10)

2 动力学仿真计算

2.1 无导弹发射时战车的运动情况

以两栖战车行进速度u=0 m/s、车辆所受浮力为0 N、海浪为四级海况(风速U=6.7 m/s),航向角γ=180°为初始条件,得到40 s内战车的前进速度u、线位移z、横摇角位移φ和纵摇角位移θ随时间变化曲线如图2～图6所示。

图2 车辆前进速度随时间变化曲线Fig.2 Curve of vehicle forward speed with time

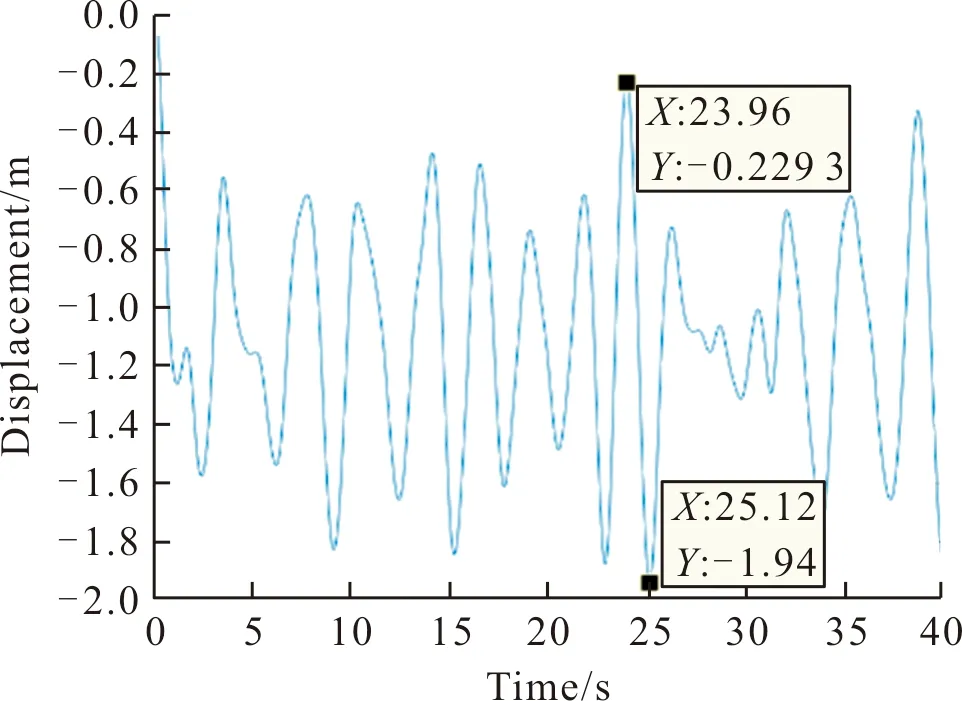
图3 车辆Z向位移随时间变化曲线Fig.3 Time variation curve of vehicle Z-direction displacement

图4 车辆横摇角度随时间变化曲线Fig.4 Curve of rolling angle with time

图5 车辆纵摇角度随时间变化曲线Fig.5 Curve of vehicle pitch angle with time

由图2可知,车辆在t=0 s时,前进速度为u=0 m/s;施加驱动力后,在t=2.52 s时,前进速度u=5.55 m/s,即u=20 km/h;随后前进速度u在18.25～21.75 km/h内波动。

由图3可知,车辆在t=0 s时,车辆垂向位移z=0 m;因重力大于浮力,车辆下沉,直至重力与浮力相等,车辆在海浪作用下做起伏运动。

由图4～图5可知,车辆的横摇角度在-0.003 2～0.003 6 rad之间变化,纵摇角度在-0.20～0.15 rad之间变化。

2.2 导弹初始扰动分布情况

因为海浪激励是随时间变化的随机激励,所以单独时刻发射导弹得到的导弹初始扰动并不能体现分布规律。从图2～图5可以看出:在施加随机海浪激励10 s后,战车运动姿态趋于稳定。因此选取在10～35 s时段内,每隔0.05 s进行一次计算,得到导弹初始扰动数据,采用Kolmogorov-Smirnov测试方法判断其分布情况,在显著度α=0.005的情况下,可以得出俯仰角速度、偏航角速度和滚转角速度符合正态分布。

发射水平射角30°、高低射角15°工况下,导弹的俯仰角速度、偏航角速度和滚转角速度分布情况及拟合正态分布曲线如图6～图8所示。

图6 滚转角速度分布情况Fig.6 Roll angle velocity distribution

图7 俯仰角速度分布情况Fig.7 Pitch angular velocity distribution

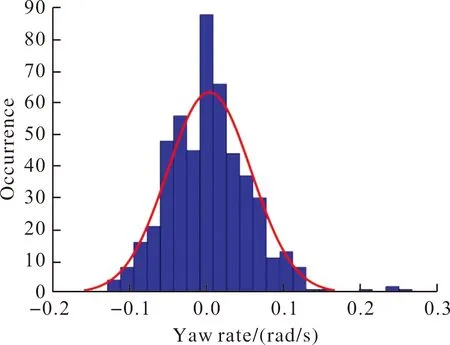
图8 偏航角速度分布情况Fig.8 Yaw angular velocity distribution

2.3 其余工况计算结果分析

文中研究内容为导弹发射架水平射角和高低射角对于导弹初始扰动的影响。其中水平射角可以分为0°、30°和60°三种情况、高低射角可以分为0°和15°两种情况,将水平射角和高低射角两两组合,一共可以得到6种工况。表1～表6为6种工况多次计算得到的初始扰动数据分布规律统计表。

表1 工况1(水平射角0°、高低射角0°)Table 1 Working condition I (horizontal shooting angle 0°, high and low shooting angle 0°)

表2 工况2(水平射角30°、高低射角0°)Table 2 Working condition II (horizontal shooting angle 30°, high and low shooting angle 0°)

表3 工况3(水平射角60°、高低射角0°)Table 3 Working condition III (horizontal shooting angle 60°, high and low shooting angle 0°)

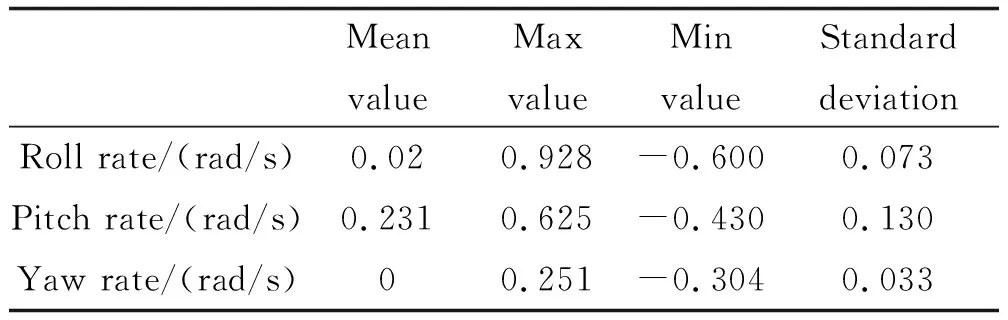
表4 工况4(水平射角0°、高低射角15°)Table 4 Working condition IV (horizontal shooting angle 0°, high and low shooting angle 15°)

表5 工况5(水平射角30°、高低射角15°)Table 5 Working condition V (horizontal shooting angle 30°, high and low shooting angle 15°)

表6 工况6(水平射角60°、高低射角15°)Table 6 Working condition VI (horizontal shooting angle 60°, high and low shooting angle 15°)

2.4 因素影响程度分析

计算数据拟合正态分布后,主要参数有2个:均值μ和标准差σ。为了研究初始扰动分布情况,选取各个工况计算得到的[μ-3σ,μ-3σ]区间中绝对值最大的值来描述该工况下可能对弹的初始扰动影响最大值。

表7 滚转角速度正交分析表Table 7 Orthogonal analysis table of roll angle speed

表8 俯仰角速度正交分析表Table 8 Orthogonal analysis table of pitch angular velocity

表9 偏航角速度正交分析表Table 9 Orthogonal analysis table of yaw angular velocity

根据极差R大小可以得出:

1)高低射角角度对弹的初始扰动影响大于水平射角角度影响。

2)水平射角角度大小对滚转角速度变化影响较大,对偏航角速度变化影响较小,对俯仰角速度变化基本无影响。

3)高低射角角度大小对滚转角速度变化影响较大,对偏航角速度变化影响较小,对俯仰角速度变化基本无影响。

根据K1～K3的值可以看出:

1)滚转角速度和偏航角速度分布偏离零点最小工况为水平射角0°、高低射角0°。

2)俯仰角速度分布偏离零点最小工况为水平射角60°、高低射角15°。

3 结论

利用动量定理和动量距定理,模拟两栖战车在四级海况下迎浪行进的过程,计算导弹发射初始扰动分布情况,得出以下结论:

1)导弹的初始扰动符合正态分布情况。

2)导弹的俯仰角速度较大,绝对值在0.2～0.3 rad/s;滚转角速度和偏航角速度绝对值小于0.1 rad/s。

3)高低射角对于初始扰动影响较大,水平射角影响程度较小。