基于全要素生产理论对数字经济新动能的测度

高畅 韩海波 鲁文梦

摘 要：全要素生产率与产业高质量发展密切相关，数字经济作为一种新型生产要素，已与劳动、资本、技术进步等投入要素并列。为了对我国数字新动能进行统计测度研究，本文采用DEA—Malquist指数法测算全要素生产率，并对其进行分解，测算数字新动能对其的贡献程度；采用索洛残差与DEA—Malquist指数相结合的方法对照分析全要素生产率及其变化趋势，构建包括劳动、资本和数字经济指标的三要素C-D生产函数模型测算我国2012—2019年的全要素生产率，再与两要素的C-D生产函数模差值得出残差便可以解释为数字经济给我国产出带来的影响。结果显示，运用索洛残差法得到2012—2019年我国全要素生产率变化趋势与运用DEA-Malmquist指数法得到的结果大致相似，即数字经济全要素生产率趋势自2011年逐年增加，且增速较快。当前，数字经济已融入人们的生产生活中，且不断提升，但全要素生产率在各个地区间存在一定的差异。

关键词：数字经济；全要素生产率；DEA-Malquist指数；索洛残差；科布道格拉斯生产函数

本文索引：高畅，韩海波，鲁文梦.<变量 2>[J].中国商论，2023（07）：-004.

中图分类号：F124 文献标识码：A 文章编号：2096-0298（2023）04（a）--04

1 绪论

随着全球经济的飞速发展，许多国家越来越重视数据及人工智能对全社会未来的影响，发展数字经济已成为一项重要课题且引起无数学者的关注。本文从全要素生产理论角度，对数字经济的问题进行了深入研究，探索数字经济的新动能。

1.1 研究背景

2019年，G20国家的数字经济都有着不同程度的增长。从国家层面来看，美国数字经济规模最高，以13.1万亿美元居首位，中国位居第二、德国第三名、日本第四名和英国第五名。在数据信息时代，发展数字经济已成为各国在国际中争夺话语权的有力手段。如今我国面临初生儿生育率下降、人口老龄化等问题，传统劳动力要素对经济的贡献程度逐渐收缩。1998年4月，美国商务部正式提出了数字经济概念，《新兴的数字经济》报告中提出的这一理论迅速引起各国的重视。近几年，许多国家在重要的国际会议上更是频繁地引入数字经济等相关议题。由于国情不同，我国数字经济方面的研究相对美国起步较晚，直至2010年之后，数字经济研究范围才有所扩大。数字经济在很大程度上改变了我国经济的生产、消费和分配模式，给人们提供了更高效的经济运作模式。

1.2 国内外研究现状

数学家科布（C.W.Cobb）和经济学家道格拉斯（Paul H. Douglas）在20世纪30年代提出了传统的科布道格拉斯生产函数，在一般的生产函数形式下引进技术进步这一因素来探究投入与产出的关系。20世纪60年代，美国著名经济学家肯德里克提出全要素生产率的概念（简称TFP），反映在生产过程中无法被定量分析的那些复杂要素对生产率的贡献，如技术进步、人力资本等。随着计算机的普及及网络的覆盖，数据已经成为一项重要的生产要素而与资本及劳动等并列对产出进行分析（王磊，2020）。范合君、吴婷（2020）对中国数字化的程度进行了系统测算并构建有关数字经济的指标体系。焦帅涛、孙秋碧（2020）研究我国数字经济发展与产业结构升级间的联系。许宪等（2021）系统研究了数字化转型背景下中国经济社会统计应用面临的风险与挑战。杨慧梅、江璐（2021）从生产率高低与区位优势两个方面，克服内生性等问题，系统阐释数字经济对全要素生产的影响。前人文献证明了数字经济这种新的要素不仅提高了本地区的全要素生产率，还对周围地区有着明显的溢出效应，本文对我国继续探索新的经济增长路径提供了理论支撑与政策参考。

2 研究设计

2.1 研究方法

2.1.1 DEA—Malmquist指数法

本文构建了t至t+1期的Malquist指数，即

其中，和表示在t期和t+1期的技术下t时期的距离参数；和表示在t期和t+1期的技术下t+1时期的距离函数。

DEA－Malmquist（Tfpc）指数在以规模收益不变的前提下可以分解为两方面。一方面是技术效率变化指数（Effch），另一方面是技术进步指数（Techch）。技术效率变化指数可进一步划分为纯技术效率变化指数（Pech）和规模效率变化指数（Sech），表示公式为：

2.1.2 索洛殘差法

索洛残差法简单来说，就是根据生产函数，利用产出的增长率减去各个基本要素增长率后得到的差值，即全要素增长率。C-D生产函数表达式为，由于假定规模报酬不变（α+β=1），则公式可变换为：

假定技术进步水平系数At保持不变，Yt为实际产出，Kt为实际资本投入，Lt为实际劳动投入。公式（4）为C-D生产函数两边分别取对数的形式；公式（5）中t代表全要素生产率增长率，b代表实际资本增长，c代表劳动增长，α为公式（4）线性回归所得估计出的系数，代表实际资本的产出弹性系数，β为实际劳动力的产出弹性系数。

2.2 数据来源及指标选取

2.2.1 数据来源

本文遵循科学性、可靠性、全面性等原则，从经济发展角度，选取我国各地区生产总值、固定资本形成总额、劳动就业人数、规模以上工业企业研究与实验发展（R&D）经费支出和能源的数据。省级层面的数据由于规模以上工业企业的R&D经费支出公布不全，本文进行填补后生成2011—2019年29个省份（不含新疆、西藏）的面板数据。数据来自国家统计局、《中国科技统计年鉴》《国家统计年鉴》、各省份统计年鉴等。

2.2.2 指标选取

（1）产出（Y）。为了实现全要素生产率的测算与分解过程，将各地区的国内生产总值作为产出指标，且根据GDP平减指数调整为以2001年为基期的各地区的实际生产总值。

（2）资本投入（K）。资本投入大多用资本存量表示。使用各省份固定资本形成总额，将其折算为资本存量。本文参考大多数文献的做法，定折旧率为5%，以2002年为基期。

（3）劳动投入（L）。使用各地区城镇就业人数来衡量。

（4）科学技术投入。结合数据的相关性和可获得性，选取规模以上工业企业研究与试验发展（R&D）经费支出作为衡量科技进步的一种生产投入。

3 实证分析

3.1 DEA-Malmquist指数法测算全要素生产率

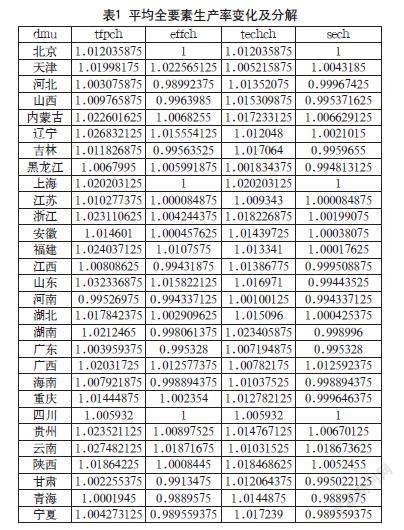
经Stata16测算结果显示，2011—2019年我国29个省份中，有28个省份的数字经济在全要素生产率上均有不同程度的增长，其中云南、福建、浙江和贵州增长幅度较大。河南省是数字经济全要素生产率唯一呈负增长的省份。由表1可以看出，浙江的技术效率呈现下降趋势。数字经济对各省技术效率在空间上的差异较为显著，存在区域异质性，其中甘肃、青海、宁夏、海南、重庆、湖南、广东、江西、山东、河南、河北、山西、吉林和黑龙江的数字经济规模效率均呈下降趋势，北京、上海和四川的数字经济规模效率保持不变，其余省份均上升，如表1所示。

3.2 索洛残差法测算全要素生产率

3.2.1 构建三要素的C-D函数模型

通常使用C-D模型作为生产函数的具体表现形式，除去已有的资本和劳动力要素，如将规模以上工业企业R&D经费支出作为第三种要素投入，我国产出对应的生产函数为：

Yt=At KαLβRγ   （6）

其中，t代表时期，Yt代表地区生产总值；At为希克斯中性技术系数，由于技术系数可能随时间变化，因此把技术的具体形式设定为At=A0ebt，用来反映广义的技术进步。K、L、R分别代表资本存量、劳动力和数字经济的投入。A0、b均为常量，α、β、γ分别代表资本、劳动力和规模以上工业企业R&D经费支出的产出弹性。取自然对数后，由于索洛残差法需假定规模收益不变，则α+β+γ=1，公式（6）变为：

（7）

此时，可以大致理解为全要素生产率增长等同于技术进步率。利用基于最小二乘法的回归方程可以得到A0、b、β、γ的估计，运用公式即可得到α，从而求出，t1～t2年的TPE增长率为。

但需要明确的是，在实际情况中，并不一定满足理想化规模收益α+β+γ=1假设条件，因此在具体测算之前需对这一前提进行检验，使用Wald方法检验，结果如表2所示。

表2 三要素模型Wald检验结果

原假设 F统计量值 P值

α+β+γ=1 0.05 0.8172

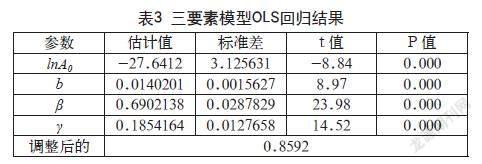
OLS回归结果显示，F统计量的P值大于0.05，表明在5%的显著性水平上不能拒绝原假设，因此我国的生产函数在2012—2019年表现为规模报酬不变。对公式（7）进行约束条件为γ=0的Wald检验，F统计量值为120.63，P值为0.000，表明当不加入规模以上工业企业R&D经费支出时，模型的解释能力明顯减弱，此时拒绝原假设。模型中需要保留R&D经费支出变量，使用Stata软件对公式（7）进行OLS回归分析，结果如表3所示。

3.2.2 构建两要素的C-D函数模型

我国数字经济产出对应的生产函数为：

解释同三要素模型，当规模收益不变时，有α+β=1，公式（8）变为：

此时，全要素生产率的增长率等于其他复杂因素如数字经济、技术创新带来的产出增长。Wald检验中，F值为86.02，P值为0.011，在显著性为1%的情况下接受规模收益不变假设。用OLS方程对数数据的拟合结果较好，可将各参数的估计值带入相关的公式中即可求得两要素2012—2019年数字经济的TFP，如表5所示。从TFP增长率正负波动来看，两要素模型在2016年出现过TFP迅速下降的情况，而三要素模型在2012—2019年一直呈递增趋势。两种模型均显示2016—2018年我国数字经济的TFP有较大幅度的提升。

4 结语

4.1 结论

本文通过上述实证分析的结果可以看出，无论是运用索洛残差法还是运用DEA-Malmquist指数法，得到的全要素生产率变化趋势的结果大致相似。数字经济全要素生产率趋势自2011年逐年增加，且增速较快，具体结论如下：

（1）从中国数字经济整体发展趋势来看，2013年之前中国数字经济全要素生产率呈负增长趋势；2013年开始数字经济推动全要素生产率不断增长，自此数字经济全要素生产率均处于正增长状态。由此可以推断出各行业的数字动能提高是其TFP改善的主要原因。

（2）从各省市的实证结果分析得出，全要素生产率在我国各省份存在明显区域异质性。除河南以外，其余省份数字经济TFP都呈递增趋势。从整体来看，数字经济是我国生产生活及经济增长的重要动力，但地区间发展不均衡的问题仍存在。

（3）以北京为例，先用索洛残差法对全要素生产率进行测算，再分别对两要素模型和三要素模型做OLS回归，计算全要素生产率对产出的贡献值。整体来看，TFP增长率的均值显著大于1且有明显递增趋势，虽存在小幅波动，但我国2012—2019年数字经济的TFP整体呈上升趋势，效果显著。

4.2 政策建议

4.2.1 提高对数字经济重要性的认识

与互联网前沿相关的技术还有很多，例如软件、通信技术、数字显示等，这些前沿技术可以更好地促进数字经济的发展，带动经济的增长。数字经济未来的发展，主要包括两个方面：一方面，建设与完善互联网的基础设施；另一方面，发展与互联网结合的前沿技术。简单来说，就是加快互联网建设的步伐，扩大光纤覆盖面积，使全体人民都可以共享数字经济带来的红利。若提高此方面的认知能力，未来经济发展、产业结构升级都将有不同程度的提升，促进其他产业与数字经济的良性协同发展，提高未来我国在各个领域上与其他国家的竞争力。

4.2.2 提供更强的技术创新支持力度

在数字经济的发展过程中，加快新动能发展有利于壮大技术创新。由于互联网发展迅猛，在其发展初期，数字经济通过在网络市场上获取的用户信息基础，前沿的数字经济技术产业得到了促进，逐渐在经济增长过程中占据主导地位，如我国国防军工中对前沿数字技术的应用，军民合作的政策使得数字技术向民用领域的扩散加快，使数字经济发展有更好的环境。

4.2.3 鼓励数字经济龙头企业做强做大，引领数字经济新格局

一方面，需国家政策支持我国数字经济强劲企业与发达国家企业的合作交流，大力输出我国在人工智能、5G 等领域的先进技术，积极参与国际合作；另一方面，需要增加与发展中国家的信息交流、完善信息站点的基础设施建设，把我国成功的数字经济商业模式、理论方法、实践经验推广至更多的城市及国家，一起联手共同进步，为我国数字经济的发展开创明天、引领未来。

参考文献

许宪春，张美慧.中国数字经济规模测算研究：基于国际比较的视角[J].中国工业经济，2020（5）：23-41.

吴志刚. 重构数据生产关系培育数据要素市场（上）[N]. 中国信息化周报，2021-03-22（12）.

范合君，吴婷.中国数字化程度测度与指标体系构建[J].首都经济贸易大学学报，2020，22（4）：3-12.

焦帅涛，孙秋碧.我国数字经济发展对产业结构升级的影响研究[J].工业技术经济，2021，40（5）：146-154.

许宪春，张美慧，张钟文.数字化转型与经济社会统计的挑战和创新[J].统计研究，2021，38（1）：15-26.

杨慧梅，江璐.数字经济、空间效应与全要素生产率[J].统计研究，2021，38（4）：3-15.