一种适用于弹性飞机飞行仿真的补丁方法

王培涵，吴志刚，，杨超，孙晓旭

1．北京航空航天大学 航空科学与工程学院，北京 100191

2．海鹰航空通用装备有限责任公司，北京 100070

飞行仿真技术是以飞行器的运动为研究对象，面向复杂系统的仿真分析方法[1-2］，是计算飞行力学研究的重要领域。传统飞行力学主要研究低速飞行器的运动特性和安全性，并逐步衍生出有控飞行力学、计算飞行力学等诸多领域[3-4］。在此基础上发展出的飞行仿真技术，大多基于刚性假设，在运动响应分析、飞行控制系统设计等方面展开研究。

随着航空技术的飞速发展，现代飞机呈现出轻结构、大柔性和低阻尼等特点[5］，气动弹性问题成为不可忽视的重要因素，使得飞行仿真中的刚性假设在特定情况下不再适用。弹性飞机飞行仿真的关键，在于刚体运动与弹性变形之间的耦合关系，需考虑结构的弹性效应、不同模态间的气动力耦合等诸多因素，情况较复杂。国内外学者大多将刚体自由度和弹性自由度统一考虑，选取适当的坐标系构建弹性飞机运动方程，包括平均体轴系、准坐标系及瞬态坐标系等[6］。

目前，平均体轴系在弹性飞机飞行仿真研究中应用较为广泛。Waszak 等[7-8］通过拉格朗日方程和片条理论构建弹性飞机的运动方程，实现了基于刚弹耦合的弹性飞机飞行仿真，为后续研究工作提供了理论基础。Schmidt 等[9］将弹性自由度添加到刚性飞机动力学模型中，统一考虑刚体和弹性模态广义坐标，并以B-1 和高速商用运输机为例，深入研究了基于刚弹耦合的弹性飞机飞行仿真。Saltari 等[10］推导了全耦合方程，构建了配平状态下小扰动线化气动弹性的状态空间方程，系统地讨论了惯性和气动耦合效应对稳定性、动态响应的影响。Liu 等[11］基于非线性耦合动力学方程对弹性飞机进行了仿真，研究了几何非线性对弹性飞机运动方程的影响。Zúñiga等[12］针对弹性飞行器进行了基于刚弹耦合的飞行仿真，深入探讨了弹性效应对短周期和长周期模态的影响。孙若琳[13］基于气动力降阶模型开展了弹性飞机飞行仿真研究，师妍等[14-15］进一步研究适用于飞行仿真的非线性、非定常气动力降阶建模，实现了低速飞机在强阵风作用下的飞行仿真分析。

由于刚弹耦合动力学方程需统一考虑刚体和弹性的自由度，有学者提出了将刚体和弹性模态广义坐标分开考虑，以简化弹性飞机飞行仿真的建模过程。Looye[16］结合气动模型，提出了仅考虑动力学增量对刚性飞机运动方程影响的研究思路。Kier 与Looye[17］合作，在小扰动线化模型中，利用该方法改进非线性运动方程的动态机动载荷分析模型，形成了统一的机动和阵风载荷建模分析方法。Castrichini 等[18］应用该思想，研究半气动弹性铰链装置对气动弹性、飞行动力学耦合效应的影响。Chen 等[19］以此思路为基础，设计了非线性动态飞行仿真（Dynamic Flight Simulation，DFS）工具，结合飞行动力学和气动弹性力学，实现了基于小扰动线化方程的弹性飞机飞行仿真。而后，美国空军研究实验室在StS-RtS 仿真程序中应用该飞行仿真工具，提高了载荷计算精度。Tuegel 根据DFS 便于集成的特点，在计算飞机寿命周期的数字孪生技术中，应用该方法考虑气动弹性对飞机疲劳载荷的影响，提高了寿命周期的计算精度[20］。

与刚性飞机的飞行仿真相比，基于刚弹耦合的弹性飞机建模方法相对复杂，使得动力学特性、控制系统设计等的研究和验证工作需要重新开发，不利于其在实际工程中的应用。分开考虑刚体和弹性自由度，通过引入气动弹性效应将原有刚性飞机飞行仿真推广到弹性飞机，具有便于集成的特点。但该方法基于小扰动线化模型，未推广至非线性6 自由度全量方程。而实际工程应用中，全量方程的刚性飞机飞行仿真占比较大，该方法的应用受到了限制。另外，这种分开考虑的思想在国内外研究中相对较少，具有深入分析的价值。

针对以上这些问题，本文提出了一种适用于弹性飞机飞行仿真的补丁方法。结合刚弹耦合动力学方程的特点，拆分广义气动力、提取出与弹性效应相关的部分叠加到刚性飞机运动方程中，以实现弹性飞机运动方程的求解；同时将弹性振动导致的测量信号增量叠加到刚性飞机运动响应中，实现了弹性飞机测量信号的模拟。这两部分共同构造了反映气动弹性效应的“补丁模块”。本文的补丁方法通过置入该模块，将6 自由度全量方程刚性飞机的飞行仿真推广到弹性飞机的飞行仿真。该方法能充分利用原有刚性飞机仿真模型，简化了弹性飞机的建模和验证过程，便于稳定性分析和控制系统设计等工作开展。

1 飞行仿真补丁方法总体思路

刚性飞机[2，21］和基于刚弹耦合的弹性飞机飞行仿真[7-8］，分别是采用6 自由度刚性飞机运动方程和刚弹耦合动力学方程来实现的，如图1 和图2所示。

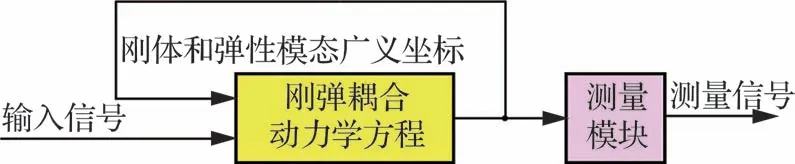
图2 基于刚弹耦合的弹性飞机飞行仿真Fig.2 Flight simulation of flexible aircraft based on rigid-elastic coupling equations

相比于6 自由度刚性飞机运动方程，图2 中的刚弹耦合动力学方程的特点在于引入了n个弹性自由度，方程总个数变为6+n。该变化使得飞行仿真从刚性飞机推广到弹性飞机时，飞行动力学模块的仿真程序需要做较大幅度改动。

通过分析刚弹耦合方程，考虑将广义气动力拆分，把飞机的弹性效应整理为气动弹性状态空间方程、刚体气动力的增量等几部分，并将它们组合成“补丁模块”。将补丁模块与已有的刚性飞机飞行仿真程序相结合，实现了弹性飞机的飞行仿真，飞行仿真方法的总体思路如图3 所示。图3 中的“刚性飞机运动方程”模块[22-23］已是成熟技术，这里不作赘述，本文重点讨论“补丁模块”的构建。

图3 基于“补丁模块”的弹性飞机飞行仿真示意图Fig.3 Schematic diagram of flight simulation of flexible aircraft based on patch module method

2 弹性飞机动力学模型

在弹性飞机的飞行仿真中，选择平均体轴系，可减弱或消除刚体和弹性自由度的惯性耦合，飞机的刚弹耦合方程可拆分成刚体运动和弹性振动方程，其中的气动弹性效应可通过弹性振动方程和广义气动力表征。

在平均体轴系下，应用拉格朗日方程推导弹性飞机的刚弹耦合动力学方程[7-9］，表达式为

式（1）为刚体动力学方程：M为飞机的质量；Ixx、Iyy、Izz为 飞 机 绕 体 轴 系3 个 轴 转 动 的 转 动 惯量；Ixy、Ixz、Iyz为交叉惯性积；U、V、W为飞行速度在体轴系3 个方向的投影；p、q、r为角速度在体轴系 上 的3 个 分 量；φ、θ、ψ为 欧 拉 角；Fx、Fy、Fz和Mx、My、Mz为除重力外，飞机所受的外力和外力矩在体轴系上的分量。式（2）为弹性振动方程：Mi、ξi、μi、ωi和Qξi分别为第i阶弹性模态的广义质量、广义坐标、阻尼比、无阻尼自然频率和广义力；n为弹性模态的阶数。整理式（1）和式（2）的右端项，得到广义力的表达式为

飞机所受的外力，包括重力、发动机推力、舵面偏转引起的惯性力，以及空气动力。重力已在式（1）左端给出，广义力的表达式为

式 中：T为 发 动 机 推 力 在 广 义 力 中 的 体 现；Mqδ为舵面耦合惯性质量为舵面偏转角的二阶导数；fA为广义气动力，由刚体运动和弹性振动耦合而成。

从式（1）和式（2）可以看出，在平均体轴系下，刚体与弹性自由度在惯性和刚度上不存在耦合，它们的耦合主要体现在广义气动力上，即为气动耦合[10］。

3 广义气动力拆分

根据刚弹耦合动力学方程，广义气动力由刚体运动和弹性振动耦合产生。因此，需定义表征刚体运动和弹性振动的变量。其中，刚体运动由状态变量η进行表征，表达式为η=

式中：X、Y为体轴系沿x、y轴方向的位移；H为高度的变化；α、β分别为迎角和侧滑角。

弹性振动由弹性模态广义坐标ξ定义，表达式为

不失一般性，式（4）中的广义气动力可表示为非线性形式，其表达式为

式中：δ为舵面偏转角；fη和fξ为刚体气动力、弹性模态广义气动力，其与η、ξ、δ存在非线性的函数关系。

在6 自由度全量方程的刚性飞机飞行仿真中，气动力一般采用非线性形式。而对于一般的弹性飞机，在线弹性小变形的假设条件下，弹性模态产生的广义气动力可以表示成线性形式。故将广义气动力拆分成非线性部分和线性增量的形式，其表达式为

式 中：h1(η，δ) 为 刚 性 飞 机 非 线 性 气 动 力；h2(η，δ)为刚体运动对弹性模态广义气动力的影响，同样为非线性形式；Δfη(ξ)和Δfξ(ξ)分别表示刚体气动力增量和弹性模态广义气动力增量，它们可由偶极子格网法[24］计算、并通过有理函数拟合技术[25-26］转化为时域形式，得到的表达式为

式中：R为对角阵，其对角线元素为气动力滞后根；Eξ为弹性模态广义坐标导数的系数矩阵。

拆分后的广义气动力中，h1(η，δ)和h2(η，δ)为非线性部分，Δfη和Δfξ为线性部分。

3.1 刚性飞机非线性气动力h1

在原有6 自由度全量方程的刚性飞机飞行仿真中，刚性飞机的气动力与状态变量η的非线性关系，一般不采用表达式的形式，而是根据气动力插值表等离散形式的数据库[2，21］，通过线性插值得到。这些数据库通常由CFD 计算、风洞试验或飞行试验等方式获得。以法向力系数Cn为例，给出气动力插值表示例如表1 所示。

表1 气动力Cn插值表示例Table 1 Examples of aerodynamic Cninterpolation

在飞行仿真过程中，根据每一时间步的飞行状态，例如迎角α和侧滑角β，可从气动力插值表中得到当前的气动力数据，用于刚性飞机运动方程求解。

3.2 弹性模态广义力h2 计算与修正

与h1有所不同，弹性模态广义气动力的非线性部分h2与弹性模态振型和气动力分布有关，一般无法通过试验获得，采用数值计算得到。若采用CFD 方法计算，时间较长，数据量也非常庞大，难以用于飞行仿真，因此本文采用面元法[27］计算。

在气动力计算时，需要给定飞机6 个刚体运动模态，包括3 个刚体平动模态Tx、Ty、Tz和3 个绕飞机质心的转动模态Rx、Ry、Rz，得到关于刚体模态的气动力影响系数矩阵。刚体模态与状态变量η之间的关系[28］为

需要说明的是：式（12）、式（13）实际上假设了φ、θ等为小量，不适合大转动等情况。最终可以得到由η和δ产生的刚体气动力和弹性模态广义气动力，这里记为和，它们的线性形式为

式中：为动压；Aηη、Aηξ、Aδη、Aδξ为 对应于η和δ的气动力影响系数矩阵，上标η和δ为矩阵对应的变量，下标η或ξ为对应刚体气动力或弹性模态广义气动力；hη0和hξ0分别为初始下洗角产生的气动力分量。

值得注意的是：在实际飞行仿真中使用的刚性飞机气动力h1(η，δ)具有非线性特性，与h1在数值上不匹配，需要对和修正。

假定由面元法计算的气动力分布在比例上是准确的，则修正思路为：将与h1相比较求得修正因子，再将修正因子应用于，从而得到飞行仿真中需要的h2(η，δ)。

以迎角α产生的气动力Cn为例，的气动力修正如图4 所示。由面元法计算得到的零舵偏时刚体气动力在体轴系的z向分量为初始下洗角产生的贡献为hz0。

首先，在刚性飞机非线性气动力h1(η，δ)中，获得零迎角、零舵偏时的法向力系数Cn0，根据Cn0与hz0的关系，计算截距的修正系数μ，即

式中：S为参考面积。

系数μ用于修正初始下洗角产生的气动力hη0和hξ0，然后对气动力影响系数进行修正。在飞行仿真的t时刻，从h1(η，δ)得到零舵偏时的非线性法向力系数则修正系数λ1(t)为

同理，由面元法计算得到的零迎角、舵偏δ产生的刚体法向气动力为从h1(η，δ)得到零迎角、舵偏δ对应的法向力系数增量ΔCn，则修正系数λ2(t)为

将 得 到 的 修 正 系 数λ1(t)、λ2(t)和μ应 用 于，得到飞行仿真中的h2(η，δ)，其表达式为

4 补丁模块构建

对比刚性飞机的气动力，式（8）增加了表征弹性效应的分量h2(η，δ)、Δfη和Δfξ。这些分量分别构成气动弹性状态空间方程、弹性模态广义气动力和刚体气动力的增量模块，用于实现弹性飞机的气动耦合，再与测量信号的弹性增量模块结合，共同构成补丁模块。

4.1 气动弹性状态空间方程

根据式（2）～式（8），忽略发动机推力对弹性振动的影响，整理弹性振动方程，表达式为

式中：M、C、K分别为广义质量、广义阻尼、广义刚度的矩阵形式；Mξδ为弹性模态与舵面偏转模态的耦合惯性质量。方程（19）左端各系数矩阵的表达式为

舵面耦合惯性质量Mqδ为6+n行的矩阵，各行分别对应式中的各广义力。其中的后n行对应矩阵Mξδ，两者之间的关系为

式中：Mηδ为刚体模态与舵面偏转模态的耦合惯性质量。

结合式（10）、式（11）和式（19），构建气动弹性状态空间方程，表达式为

各系数矩阵的表达式为

根据式（22）构建气动弹性的状态空间方程模块，输出弹性模态广义坐标及其导数ξ,以及气动力滞后根的状态变量xa用于后续计算，如图5所示。

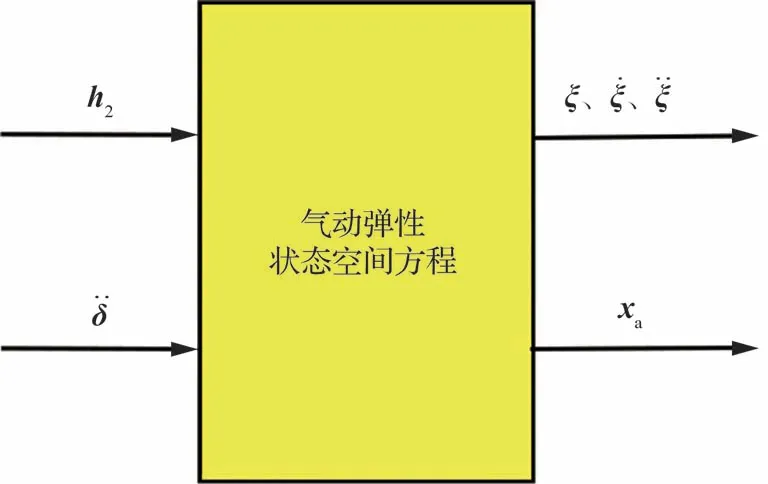
图5 气动弹性状态空间方程模块Fig.5 Module of aeroelastic state-space equation

4.2 弹性模态广义气动力

气动弹性状态空间方程需要输入弹性模态广义气动力的非线性部分h2(η，δ)。3.2 节给出了该部分的计算和修正方法，表达式如式（18）所示。因此，输入状态变量η和舵面偏转角δ，即可构建的弹性模态广义气动力模块如图6 所示。

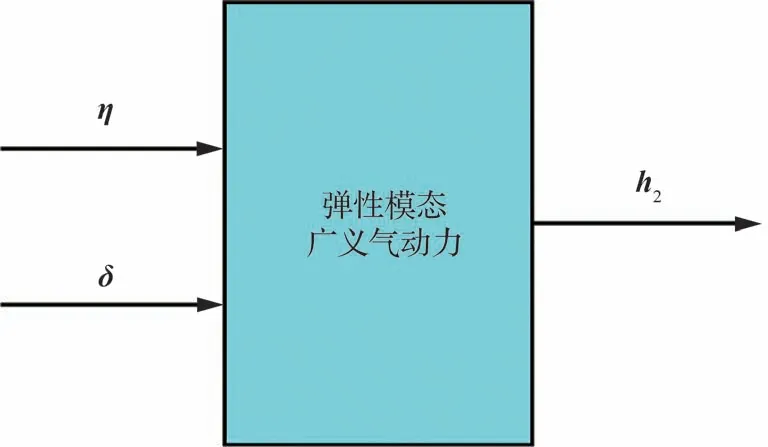
图6 弹性模态广义气动力模块Fig.6 Module of generalized aerodynamic forces based on elastic modes

4.3 刚体气动力增量

利用气动弹性状态空间方程的输出，根据式（9），计算刚体气动力的弹性效应增量Δfη，如图7 所示。根据式（8），将该增量作用于原有刚性飞机运动方程的非线性气动力h1(η，δ)中，实现刚体气动力的弹性效应修正。上述3 部分构成广义气动力的弹性效应模块，可将刚性飞机的运动方程拓展到弹性飞机的刚弹耦合动力学方程。

图7 刚体气动力的增量模块Fig.7 Module of increments of rigid aerodynamic forces

4.4 测量信号弹性增量

弹性飞机上的传感器可同时感受刚体运动和弹性振动信息，需要在原有刚性飞机运动响应的基础上，叠加弹性振动引起的测量信号增量。

在刚性飞机飞行仿真中，传感器测量飞机飞行的加速度、角速度和欧拉角。加速度的表达式为[29］

式中：x、y、z表示测量点在结构坐标系中的坐标，一般选取惯导和翼尖等需要关注的位置。

在此基础上，叠加弹性振动引起的测量信号增量，包括加速度、角速度和欧拉角的弹性效应增量，其表达式[10］为

式中：Δax、Δay、Δaz为加速度增量在体轴系3 个方向的投影；Δp、Δq、Δr为角速度增量在体轴系3个 方 向 的 分 量；Δφ、Δθ、Δψ为 欧 拉 角 的 增 量；分别为第i阶弹性模态振型的平动和转动分量。

引 入 弹 性 模 态 广 义 坐 标 及 其 导 数ξ、ξ̇、ξ̈，即可计算测量信号的弹性增量如图8 所示。将该部分与广义气动力的弹性效应模块结合，构成表征气动弹性效应的“补丁模块”。将该模块置入刚性飞机飞行仿真中，即可实现基于“补丁模块”的弹性飞机飞行仿真，如图9 所示。

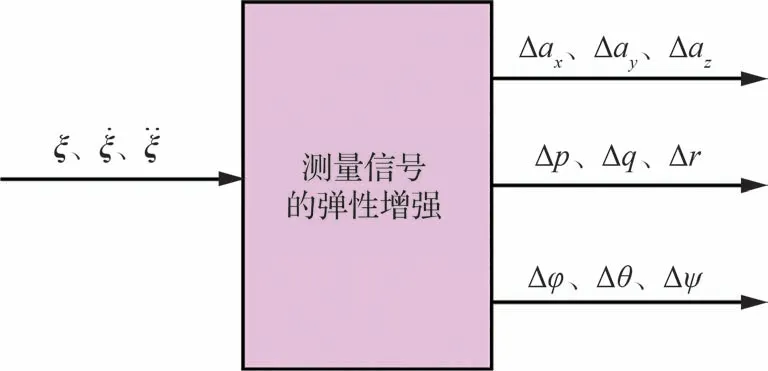
图8 测量信号的弹性增量模块Fig.8 Module of incremental measurement signals due to elastic vibrations

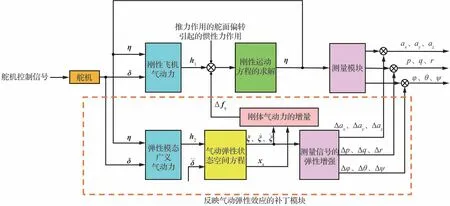
图9 基于“补丁模块”的弹性飞机飞行仿真Fig.9 Flight simulation of flexible aircraft based on patch module method

5 算例验证

以某大展弦比无人机[15］为研究对象，如图10所示，验证基于“补丁模块”的弹性飞机飞行仿真分析方法的可行性和准确性。根据飞机有限元模型，应用模态截断法[8］，选取前20 阶弹性模态进行验证。主要弹性模态频率如表2 所示，弹性模态振型如图11 和图12 所示。

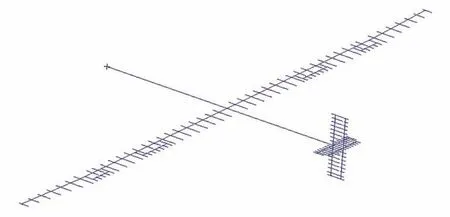
图10 某大展弦比无人机示意图Fig.10 Unmanned aerial vehicle with large aspect ratio

图12 机翼反对称一弯模态示意图Fig.12 Mode of the first antisymmetric bend

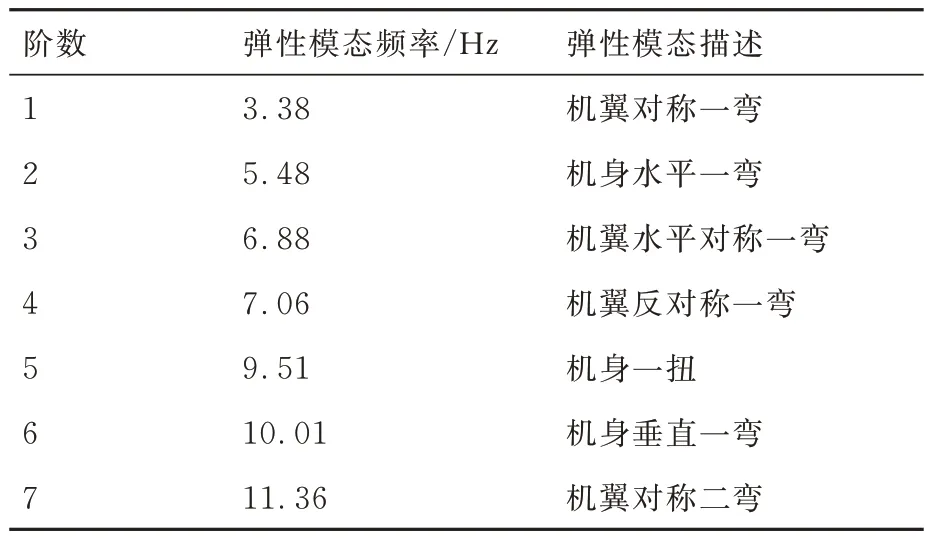
表2 主要弹性模态频率Table 2 Frequencies of main elastic modes

图11 机翼对称一弯模态示意图Fig.11 Mode of the first symmetric bend

针对该算例，研究基于“补丁模块”的弹性飞机飞行仿真分析，给出对应的配平方法，并对飞机的机动响应、闭环反馈、气动力非线性和气动伺服弹性稳定性，从不同方面对该飞行仿真方法验证。

5.1 配平方法

在飞行仿真工作开始之前，首先需要确定初始条件，即针对基于“补丁模块”的弹性飞机飞行仿真分析方法，研究飞机的配平问题。由于“补丁模块”在刚性飞机飞行仿真的基础上添加，该补丁方法保留了原有刚性飞机的配平结果。但该结果在弹性飞机在飞行仿真初期不能保持稳定，需重新给出针对弹性飞机的配平方法。

根据飞行仿真特点，给出2 种可行的配平方法，分别是刚弹耦合和闭环反馈辅助配平。刚弹耦合配平是直接应用刚弹耦合动力学方程，同时考虑刚体和弹性自由度进行配平。闭环反馈辅助配平是构建如图13 所示的迎角反馈回路辅助配平，a=0.036 为舵机参数；δ为升降舵偏转角；δc为舵机偏转指令信号；K为反馈系统的控制律。

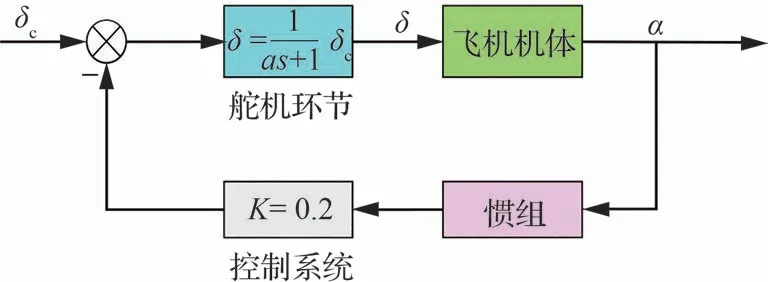
图13 迎角闭环反馈系统Fig.13 Close systems of angle of attack feedback

在高度6 km、飞行速度32.8 m/s 的飞行状态下，进行弹性飞机的飞行仿真，得到2 种配平方法的响应曲线，并与原有刚性飞机配平结果在弹性飞机中的响应曲线进行对比如图14 所示。

从图14 中可以看出，由于弹性自由度的存在，以原有刚性飞机配平结果为初始条件时，飞机响应存在明显的振荡收敛现象。但z方向（竖直方向）加速度和俯仰角速度无法收敛到0，导致俯仰角发散，弹性飞机无法保持稳定，故引入针对弹性飞机的配平方法是必要的。

图14 不同配平方法在弹性飞机中的响应曲线Fig.14 Response of flexible aircraft with different trim methods

在2 种配平方法中，刚弹耦合配平能够使得飞机处于稳定状态，不需要经过收敛过程。而闭环反馈辅助配平方法，通过迎角反馈使得加速度和俯仰角速度在1 s 内振荡收敛至0，使得俯仰角趋于稳定，满足配平要求。故这2 种配平方法都是行之有效的，可根据实际情况选择。

在工程实际中，可选择闭环反馈辅助配平的方法，减少“补丁模块”对原有刚性飞机飞行仿真的修改；而对于简单模型，选取刚弹耦合配平方法相对简单，易于实现。出于简化考虑，本文选取刚弹耦合配平方法进行后续研究工作。

5.2 俯仰机动响应

在刚弹耦合配平的基础上，研究基于“补丁模块”弹性飞机飞行仿真对机动响应的影响，分为俯仰机动响应、偏航和滚转机动响应这2 部分。在俯仰机动响应中，以如图15 所示的舵面偏转信号作为升降舵激励，对比刚性飞机飞行仿真、基于刚弹耦合的弹性飞机飞行仿真和基于“补丁模块”的弹性飞机飞行仿真，验证该补丁方法的可行性和准确性。俯仰机动响应曲线如图16 所示。

图15 舵面偏转信号示意图Fig.15 Deflection of control surfaces

由图16 的响应曲线可知，在纵向飞行仿真中，气动弹性效应使得飞机机动响应的超调量和峰值时间发生变化，导致弹性飞机的俯仰机动响应明显区别于刚性飞机。

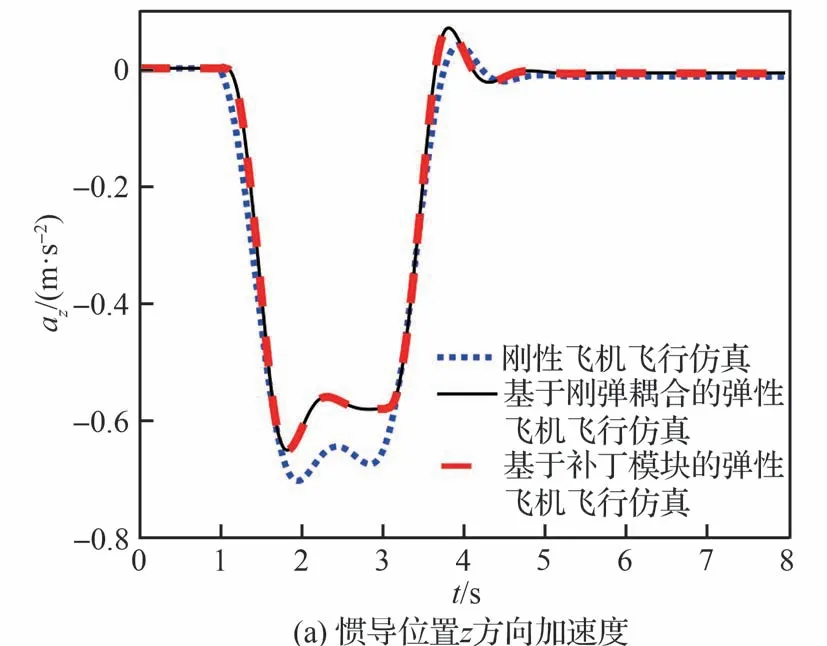
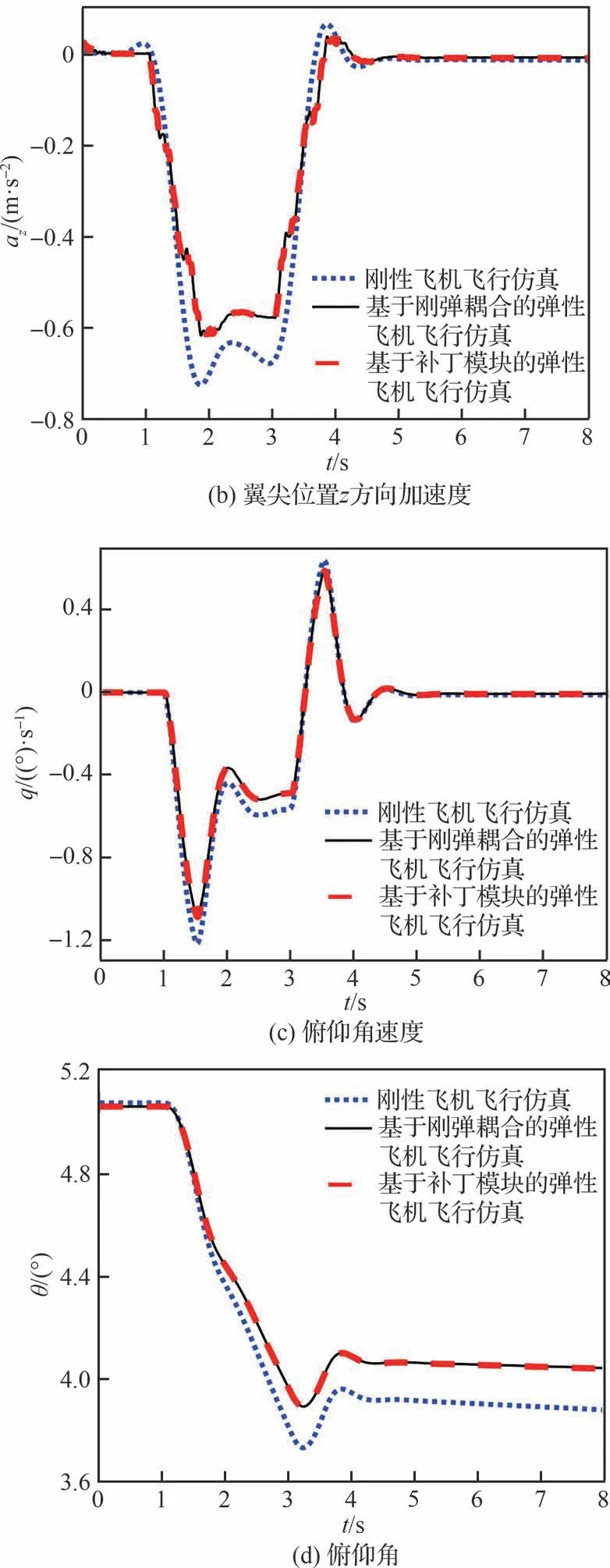
图16 俯仰机动响应曲线Fig.16 Response of pitch maneuver

对比2 种弹性飞机飞行仿真方法的结果，发现基于“补丁模块”弹性飞机飞行仿真与基于刚弹耦合飞行仿真具有一致的仿真结果。该结果表明“补丁模块”能够有效地引入气动弹性效应，将飞行仿真由刚性飞机推广到弹性飞机，验证了该方法在6 自由度全量方程刚性飞机飞行仿真俯仰通道上应用的可行性和准确性。

5.3 偏航和滚转机动响应

针对弹性飞机在6 自由度全量方程中的偏航和滚转通道，研究“补丁模块”引入气动弹性效应对偏航和滚转机动响应的影响效果。分别在方向舵和副翼上，作用如图15 所示的舵偏激励，研究表征横航向动力学特性的机动响应。其中，偏航机动响应曲线如图17 所示；滚转机动响应曲线如图18 所示。比较偏航和滚转的机动响应曲线可知，气动弹性效应对飞机横航向机动响应具有显著影响，在滚转机动的翼尖加速度响应中该现象尤为明显。

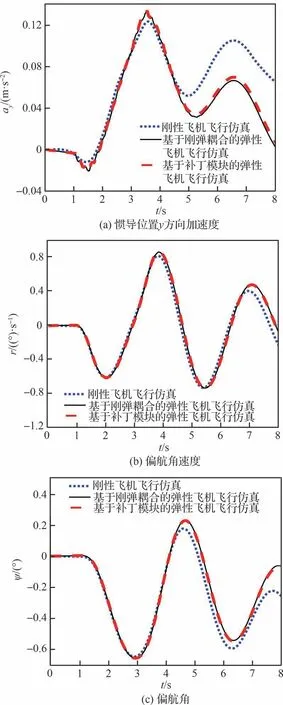
图17 偏航机动响应曲线Fig.17 Response of yaw maneuver

图18 滚转机动响应曲线Fig.18 Response of roll maneuver

基于“补丁模块”弹性飞机的飞行仿真与基于刚弹耦合的飞行仿真基本重合，能够很好地反映飞机的气动弹性效应，验证了“补丁模块”引入弹性效应在偏航和滚转通道上应用的可行性和准确性。

5.4 闭环反馈

与基于刚弹耦合弹性飞机的飞行仿真相比，“补丁模块”的优势在于，对弹性飞机进行控制系统设计、稳定性分析和验证工作时，仅需在原有刚性飞机飞行仿真模型中进行处理，减小了弹性自由度对其他设计和验证程序模块的影响。

因此，以具有简单控制系统的闭环反馈为例，验证补丁模块对闭环系统响应的影响。选取同样的无人机模型作为研究对象，设计简单的俯仰角速度反馈如图19 所示。

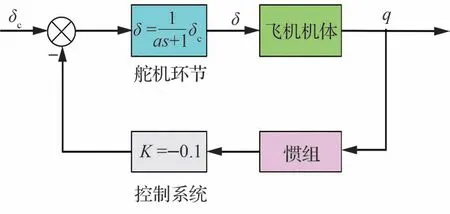
图19 俯仰角速度闭环反馈系统Fig.19 Close systems of pitch rate feedback

选取如图20 所示的阶跃信号作为升降舵机偏转指令，研究闭环系统在舵偏扰动下的俯仰机动特性如图21 所示。比较不同仿真方法的响应曲线可知，基于“补丁模块”的弹性飞机飞行仿真与基于刚弹耦合的弹性飞机飞行仿真具有相同结果，能够精确地反映闭环系统动响应特性，特别是翼尖加速度的振荡现象，验证了该方法在闭环系统响应仿真中应用的可行性和准确性，为弹性飞机控制系统设计和验证工作提供了新的思路。

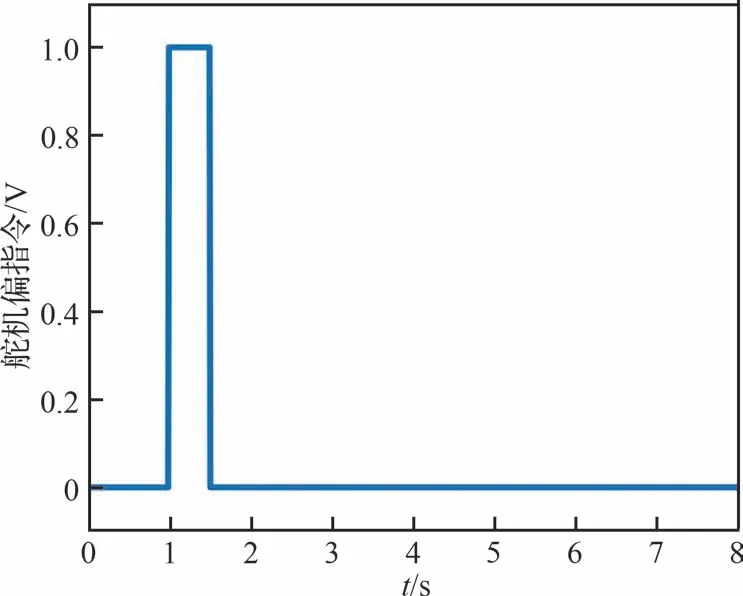
图20 舵机偏转指令信号Fig.20 Command signal of control surface deflections

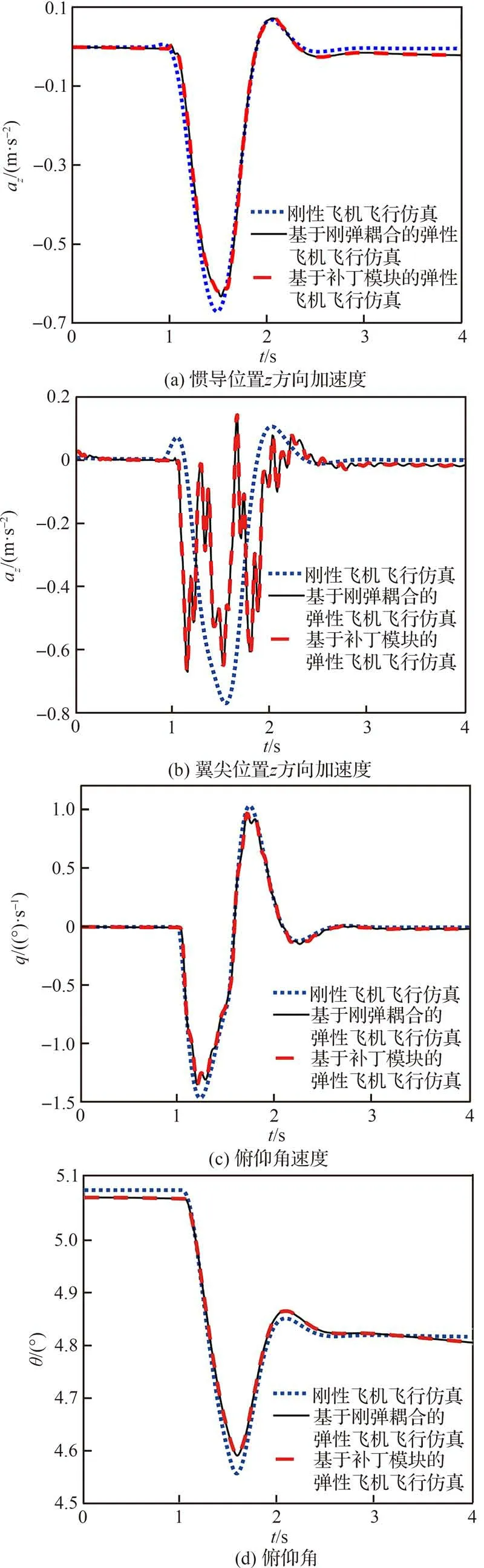
图21 闭环系统俯仰机动响应曲线Fig.21 Response of pitch maneuver in close system

5.5 非线性气动力验证

在6 自由度全量方程的刚性飞机飞行仿真中，气动力一般采用非线性形式。因此，需要验证基于“补丁模块”弹性飞机飞行仿真方法对气动力非线性情况的适用性。针对该大展弦比无人机算例，由CFD 技术分析得到法向力系数与迎角的关系如图22 所示。

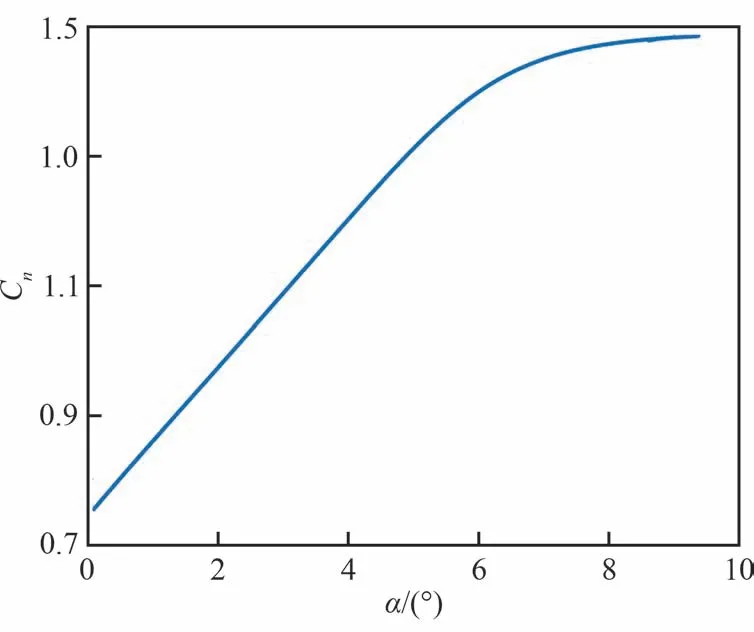
图22 法向力系数随迎角的变化曲线Fig.22 Curve of aerodynamic coefficient of normal force with angle of attack

根据该非线性法向力系数曲线，应用3.2 节对弹性模态广义气动力的非线性部分进行计算与修正，使得弹性模态广义气动力中与刚体运动相关部分，呈现出同样的非线性变化趋势。

以5.2 节中的俯仰机动响应为基础，将振幅为7°、图15 所示的激励信号作用到升降舵上，使得响应中的法向力系数达到非线性段。以第一阶弹性模态广义气动力系数为例，俯仰机动响应过程中，弹性模态广义气动力系数随迎角的非线性变化情况如图23 所示。

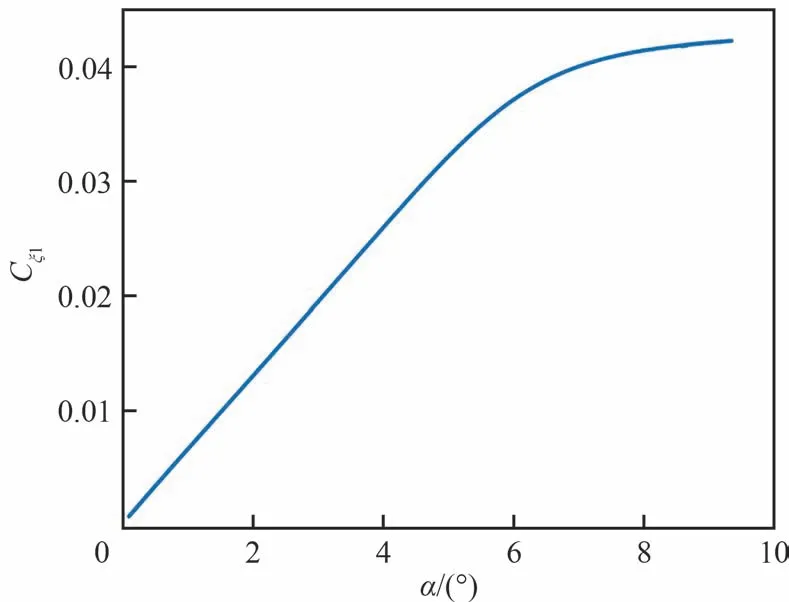
图23 第一阶弹性模态广义气动力系数随迎角变化曲线Fig.23 Curve of aerodynamic coefficient of the first elastic mode with angle of attack

应用线性和非线性气动力的刚性飞机飞行仿真、线性气动力的弹性飞机飞行仿真，以及非线性气动力的基于刚弹耦合和“补丁模块”的弹性飞机飞行仿真，进行升降舵偏转激励下的俯仰机动响应如图24 所示。根据仿真结果可知，非线性气动力改变了飞机动响应的变化趋势，惯导和翼尖处加速度、俯仰角速度响应的超调量明显降低，翼尖加速度存在明显的振荡现象；俯仰角的响应由于非线性气动力出现了不同的变化趋势。这些现象表明非线性气动力对刚性和弹性飞机的机动响应具有显著影响。

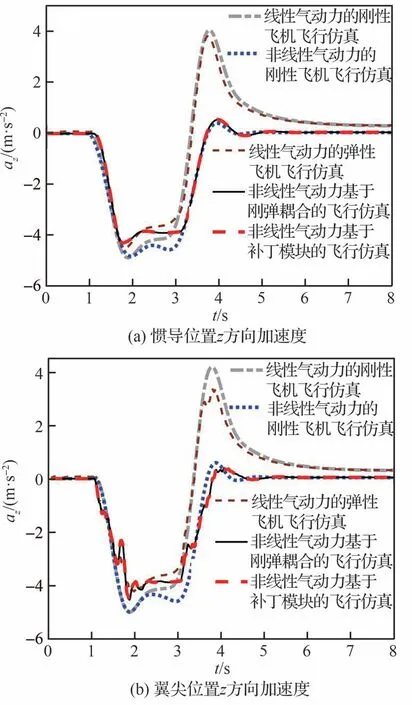
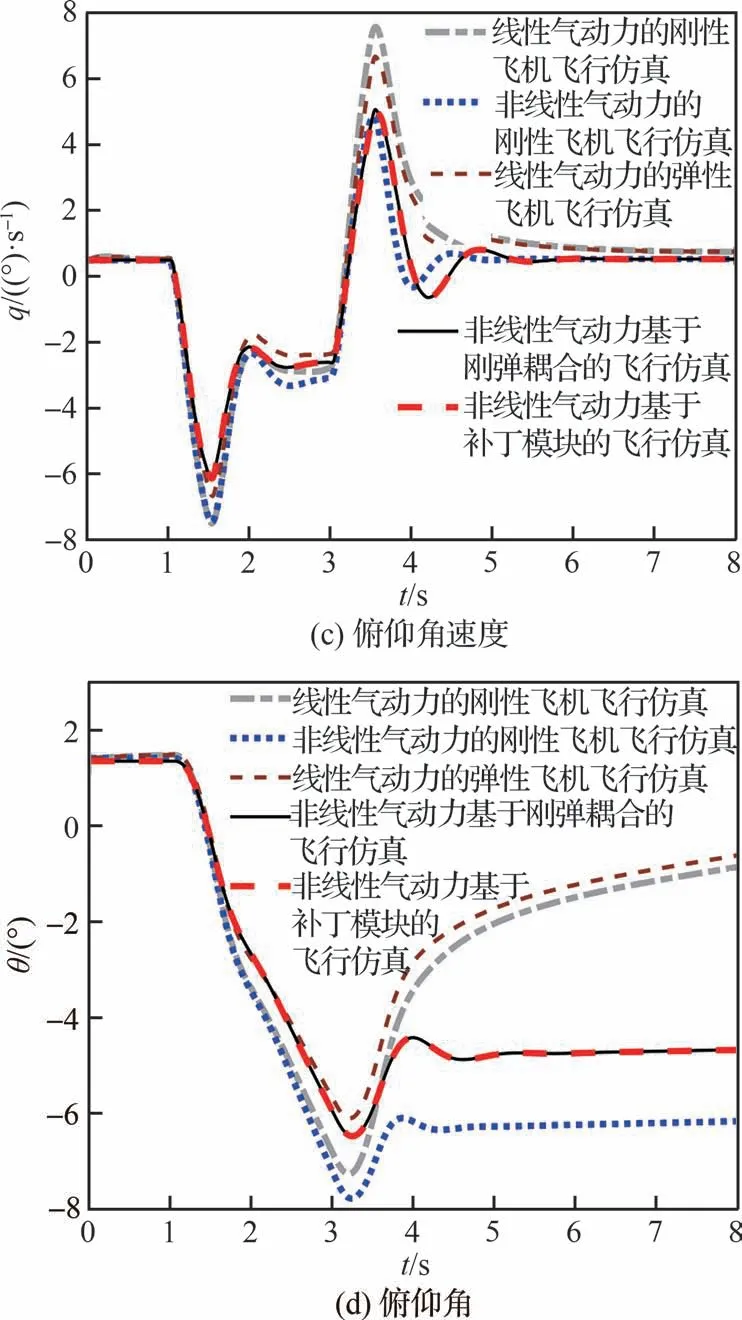
图24 气动力非线性时的俯仰机动响应曲线Fig.24 Response of pitch maneuver with nonlinear aerodynamics

对比基于刚弹耦合和“补丁模块”的弹性飞机飞行仿真响应曲线可知，在非线性气动力的条件下，“补丁模块”能够有效地引入气动弹性效应和非线性效果，与求解刚弹耦合方程具有相同的效果。因此，基于“补丁模块”的弹性飞机飞行仿真能够通过非线性气动力修正，有效地模拟弹性飞机的动响应，简化了弹性飞机飞行仿真的建模和分析流程。

5.6 气动伺服弹性稳定性

在弹性飞机闭环系统中，气动弹性和飞行控制系统存在一定的耦合现象，形成了气动伺服弹性力学[30-33］。气动伺服弹性稳定性便是其中的一个重要领域。

针对相同的算例模型，构建滚转角速度闭环反馈系统如图25 所示，δ为副翼偏转角。调节控制系统的增益系数至K=-3，使得弹性飞机的闭环系统处于临界稳定状态。此时，以如图20 所示的阶跃信号作为舵机输入，采用不同的方法进行飞行仿真分析，得到副翼偏转扰动下的动响应曲线如图26 所示。

图25 滚转角速度闭环反馈系统Fig.25 Close systems of rolling rate feedback

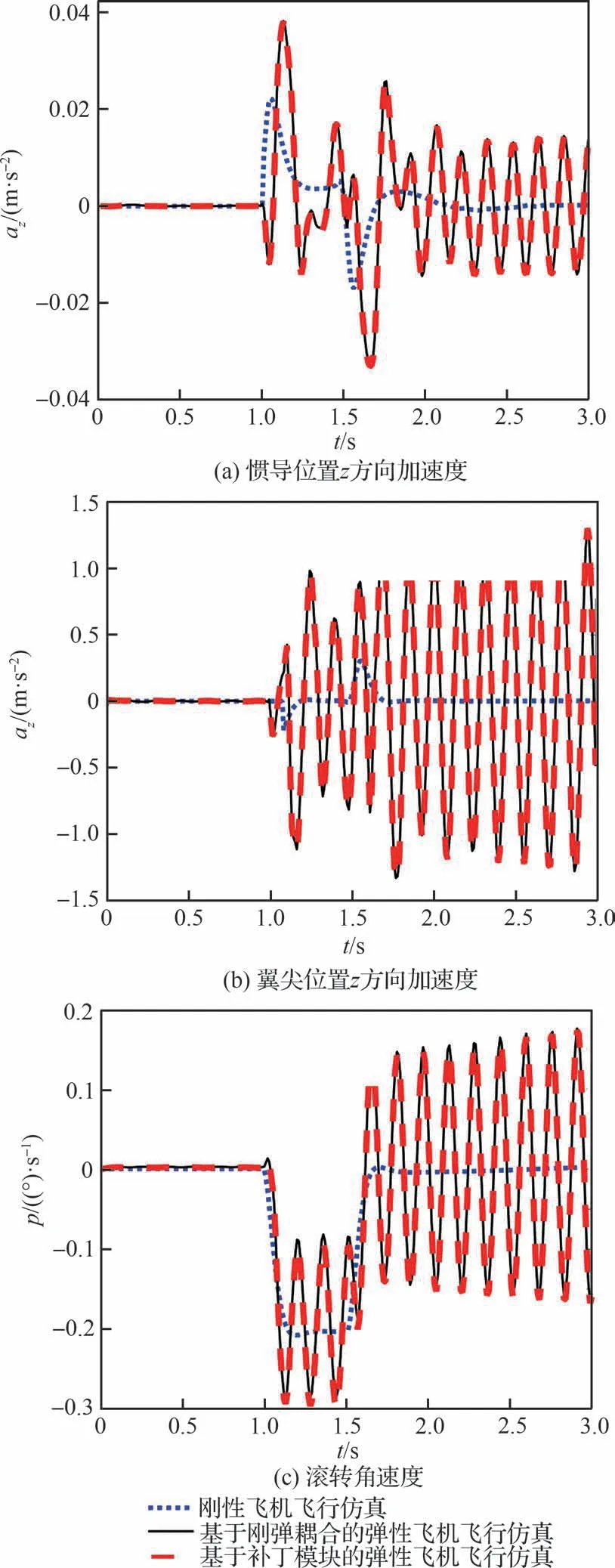
图26 气动伺服弹性临界稳定条件下的动响应曲线Fig.26 Dynamic response under condition of aeroservoelasticity critical stability

由响应曲线结果可知，刚性飞机在副翼偏转扰动下处于稳定状态，而弹性飞机由于引入气动弹性效应，气动弹性和控制系统存在一定的耦合，使得飞机处于临界稳定状态。当飞机受到副翼偏转扰动时，z方向（竖直方向）加速度和滚转角速度存在明显的振荡现象。该振荡现象的频率6.40 Hz，接近表2 中的机翼反对称一弯频率7.06 Hz。表明该临界稳定现象由机翼反对称一弯及其他模态耦合产生。

对比不同方法的仿真结果可知，基于“补丁模块”的弹性飞机飞行仿真能很好地反映气动弹性效应导致的临界稳定现象，与基于刚弹耦合的弹性飞机飞行仿真具有一致的响应结果。

因此，“补丁模块”能良好地反映弹性飞机的气动弹性效应，验证了该飞行仿真方法在气动伺服弹性稳定性分析中应用的可行性和准确性。同时，由于该方法能充分利用原有刚性飞机的飞行仿真模型，以及在此基础上设计的控制系统，丰富了气动伺服弹性稳定性的分析和验证方法。

6 结 论

1）建立了一种适用于弹性飞机飞行仿真的补丁方法。该方法通过广义气动力的拆分、测量信号弹性增量的叠加构建“补丁模块”，将该模块置入6 自由度全量方程的刚性飞机飞行仿真中，实现基于“补丁模块”的弹性飞机飞行仿真。

2）以某大展弦比无人机为例，给出了基于“补丁模块”弹性飞机飞行仿真方法的配平方法，验证了该飞行仿真方法针对飞机机动响应的可行性和准确性，显示了该方法能够考虑气动力的非线性，可应用于气动伺服弹性稳定性分析。

3）基于“补丁模块”弹性飞机飞行仿真能够在引入气动弹性效应的同时，充分利用原有刚性飞机飞行仿真的整体框架，便于将动力学特性研究、控制律设计与验证等工作直接推广到弹性飞机上，简化了弹性飞机的建模过程，为弹性飞机的飞行仿真提供了新思路。