驱动气体的密度梯度对弹丸发射速度的影响*

王马法，李俊玲，柳 森

（中国空气动力研究与发展中心超高速碰撞研究中心，四川 绵阳 621000）

超高速发射技术是地面模拟超高速撞击现象、开展超高速撞击效应研究必不可少的试验技术。轻气炮是目前超高速发射常用的设备，虽然有报道一些二级轻气炮的最高发射速度达到了10 km/s 以上[1-5]，但受到炮体材料性能的限制，常用的发射速度一般不超过8 km/s[6-7]，随着超高速碰撞领域研究的不断深入，8 km/s 的发射速度已经很难满足人们对超高速碰撞现象和机理的研究。以空间碎片为例，碎片的在轨平均速度为7～8 km/s，碎片相互撞击的平均速度约8～9 km/s[8-9]，与其他物体相撞的平均速度约10 km/s[10-11]。因此需要研究具备更高发射速度的技术。

为了实现在弹丸过载不太大的前提下获得更高的发射速度，从发射器的设计开始便一直追求能够实现匀加速发射的方法[12-13]。本文中提出一种更接近匀加速发射的方法—梯度气体驱动。梯度气体驱动是指采用重气体与轻质气体混合成具有一定梯度分布的气体作为气体炮的驱动气体，当冲击波在弹底反射后，在梯度气体中传播，一边向活塞运动，一边不断反射压缩波向弹底运动，而不需要传播到端部后再反射冲击波，因此可以缩减发射过程中冲击波的反射时间，达到持续增强弹底压力，抵消因弹丸运动产生的弹底压力下降问题。

为了分析梯度气体对发射过程和发射速度的影响，对等直径发射管中采用双气体填充的发射器结构进行理论分析，利用冲击波关系式建立弹丸运动速度的解析表达式，进而对影响发射性能的参数进行计算分析。研究结果可为梯度气体驱动技术中发射器的结构设计和装填参数选择提供参考。

1 等直径发射管模型及其作用过程波系结构

假设在一等直径发射管中存在2 种压力相同、密度不同的驱动气体，如图1 所示，其中气体1 的密度高于气体2。气体1 左端为活塞，气体2 右端为弹丸。活塞以恒定速度D向右推动驱动气体，将弹丸加速到一定的速度。

图1 发射器内弹道示意图Fig.1 Sketch of the constant cross-sectional area launch tube

根据一维不定常流理论可知，该等直径发射管作用过程的波系图如图2 所示，图中L1为气体1 的初始长度，L2为气体2 的初始长度。0 时刻活塞以速度D向右压缩气体1，形成右传冲击波，波后区为（11）区。当冲击波传播至气体界面处时，向气体2 内传入冲击波并向左反射稀疏波，在气体1 中形成（12）区、在气体2 中形成（21）区。气体2 中的右传冲击波作用在弹丸上开始驱动弹丸，同时向气体2 中反射左传冲击波，形成（22）区（在冲击波线上）。弹丸开始运动后向左传入稀疏波，形成（23）区。反射左传冲击波到达气体界面时会继续向气体2 中反射冲击波，并与（23）区的左传稀疏波相互作用形成（24）区，界面反射的右传冲击波会继续传播至弹丸底部，加大弹底压力，并在弹丸底部第2 次反射左传冲击波，第2 次反射的冲击波与（24）区相互作用形成（25）区。如此，冲击波在气体界面和弹丸底部来回反射，不断加大弹底压力。

图2 发射器作用过程的波系图Fig.2 Wave structure of the constant cross-sectional area launch tube

2 弹丸运动速度求解模型

下面利用冲击波关系式和稀疏波关系求解各区域的运动参数。（11）区参数可由冲击波关系式直接求解；（21）区和（12）区是（10）区冲击波与气体界面相互作用的结果，根据冲击波与界面的作用规律，（21）区透射冲击波，（12）区反射稀疏波，可由（21）区冲击波关系式和（12）区稀疏波方程联合界面连续条件求解。

2.1 冲击波与弹丸的相互作用

假设弹丸为刚体，且初始时刻静止，则反射冲击波波阵面（22）区上的参数可以由冲击波关系式和波后粒子速度u22=0 求得。

（23）区为以（22）区冲击波后状态为初始状态的简单波区，左行稀疏波是由弹丸运动产生的，其通解可表示为[14-15]：

弹丸的运动可以由牛顿第二定律得到：

式中：Mp为弹丸的面积质量；带下标b 的量表示壁面上的参数，即弹丸上的参数，如ub为弹丸的运动速度。

假设气体1 和气体2 均为多方气体，根据多方气体状态方程及声速的定义，有：

由于（23）区的参数u23、c23满足式(1)，壁面上的参数也应满足式(1)，有：

由式(4)可得cb(ub)，代入式(3)得到：

将式(5)代入式(2)并进行积分求解，得到：

式中：t1为弹丸开始运动的时刻，即冲击波到达弹丸的时刻。可由（20）区的冲击波速度D21求得：

式中：L2为气体2 的初始长度。

2.2 冲击波与弹丸二次作用

考虑到（23）区中，弹丸的运动速度相对较小，产生的稀疏波对压力的影响也相对较小，可假设（23）区为均匀区，其参数状态与（22）区相同，因此，反射波与界面的相互作用即为冲击波从气体2 向气体1 运动的过程。根据2 种气体的波阻抗关系可知，在界面上反射波和透射波均为冲击波。利用（13）区和（24）区的冲击波关系式和界面连续条件，可求得（13）区和（24）区的状态。

在（24）区经过界面反射的冲击波会再次与弹丸作用，此时，弹丸具有了一定的速度。为了确定此时弹丸的运动速度，先利用前面区域的冲击波速度和弹丸的运动速度求解冲击波与弹丸的二次作用时间。

根据图2 中的几何关系，可以得到反射冲击波与界面的作用时间t2为：

冲击波与弹丸第2 次作用的时间t3与冲击波速度和弹丸运动之间的关系为：

式中：xb(t3)为（23）区弹丸的运动距离，其表达式由弹丸运动速度(6)对时间积分得到：

利用数值解法可求得t3，代入式(6)，得到此时弹丸的运动速度ub(t3)。

利用（25）区冲击波的关系式和弹丸运动速度u25=ub(t3)，可以得到（25）区的流场参数p25、ρ25和c25。

与（23）区类似，采用牛顿第二定律可以得到（25）区弹丸的运动速度：

经过2 次反射后，气体2 中的冲击波已经比较小，冲击波马赫数Ma≈1，可以视为弱波或不考虑其影响。因此，在双气体驱动中，弹丸的运动速度可以表示为：

2.3 稀疏波的追赶与修正

活塞运动的终止会向驱动气体中传入稀疏波，如图2 所示，当稀疏波追赶上弹丸时，会降低弹丸底部的压力，使得加速度减小，最终降低弹丸的速度。假设活塞在时刻t4停止运动，产生向右传播的稀疏波，稀疏波以声速传播，波头运动速度为u+c，稀疏波需要依次经过（12）、（13）和（25）区。通过以上建立的波系分析方程，计算分别填充氖气、氩气和空气作为高密度气体的情况，可以得到（12）、（13）和（25）区的稀疏波波头运动速度。经分析表明，（13）区波速最小、（12）区居中、（25）区波速最大，且（12）区波速与3 个区域波速的平均值偏差不超过13%，（25）区的偏差不超过20%。同时，考虑到各稀疏波的追赶时间与各区的宽度也有关系，为简化计算，模型以（25）区的传播速度作为稀疏波的追赶速度，由此可以计算稀疏波追赶上弹丸的时刻t5。

时刻t5以后，由于稀疏波的作用，弹底压力开始迅速下降。假设此区域（26）的压力可以采用指数衰减规律进行描述：

式中：k为衰减系数。此时，弹丸的运动状态与（25）区类似，仍然是高压气体膨胀造成的加速运动，可采用式(11)计算得到，不同的是将式中的压力改为稀疏波过后的压力p26。因此，弹丸加速全过程的计算可以表示为：

3 模型验证

为了验证前述的模型，采用AUTODYN 有限元软件对直径8 mm 的等直径发射器进行仿真计算。

3.1 有限元仿真模型

发射器直径为8 mm，活塞与弹丸的距离为50 cm，气体1 为氖气、长度37.5 cm，气体2 为氦气、长度12.5 cm，弹丸材料为镁合金、厚度4 mm，发射管长度为50 cm。采用流固耦合方法进行计算，所建立的仿真计算模型如图3 所示。其中，氖气和氦气采用Euler 网格和理想气体状态方程；活塞、弹丸采用Lagrange 网格，活塞材料为钢，采用Johnson-Cook 模型和Grüneisen 状态方程，弹丸材料为镁合金，采用Steinberg Guinan 模型和Grüneisen 状态方程。弹丸和活塞材料参数均采用AUTODYN 材料库自带参数[16]。活塞运动采用自定义速度曲线边界条件设置，以7 km/s 的恒定速度向右移动40 cm。

图3 AUTODYN 仿真计算模型Fig.3 Finite elements simulation model

3.2 计算结果对比

分别改变气体初始压力（1.0、1.72、2.5 MPa）和2 种气体的界面位置（指气体界面离活塞的距离与整个充气长度的比值，即L1/（L1+L2））（55%、65%、75%），具体参数如表1 所示。采用有限元仿真对不同参数的发射器发射过程进行计算，并将式(14)中k的取值调整为-0.02 进行计算，得到的结果如表1 所示。从表1 中的结果可以看到，与有限元仿真结果相比，式(14)的计算误差不超过8.1%。同时可以看到，弹丸的发射速度随初始压力的升高而迅速增大。图4 中给出了不同初始压力下弹丸的加速过程曲线，可以看到，所建立的模型不仅能够较准确地计算最终的发射速度，同时还能较准确地计算发射速度历程。

图4 不同初始压力下弹丸的加速过程对比Fig.4 Velocity-time histories of launchers with different initial pressures

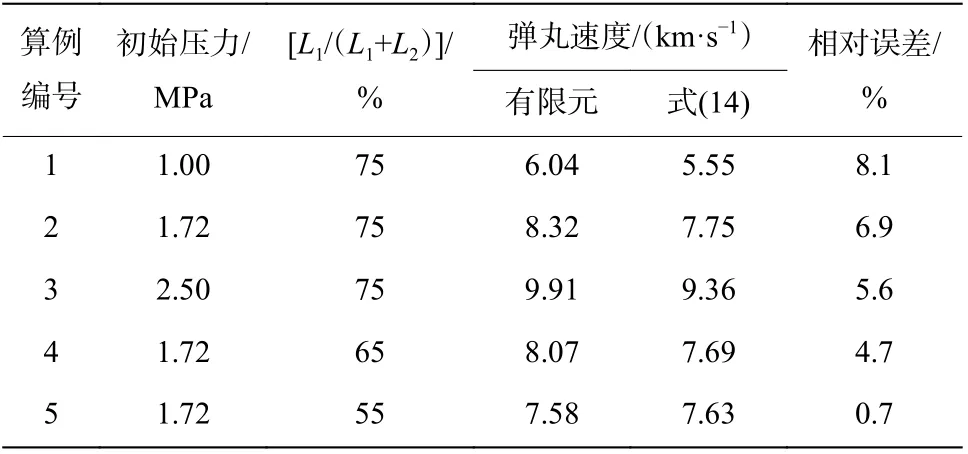
表1 理论模型与数值计算结果Table 1 Muzzle velocities obtained from simulation and analytical equation

随着初始界面位置的增加，发射速度略微增加。图5 中给出了填充1.72 MPa 气压、不同界面位置下，弹丸底部压力的变化曲线。可以看到，随着界面的位置增大，弹丸受第1 次冲击加载的时间延后，加载的时间长度缩短，第1 阶段获得的速度更低。但受第2 次冲击波加载后，弹底压力更高，二次冲击加载的时长变化不大，第2 阶段获得的速度更高，经过前2 个阶段的加载，不同初始界面位置状态下弹丸发射速度基本一致。发射速度略微增加的原因主要是，稀疏波追赶卸载后，弹底压力仍然保持了二次冲击加载后压力较高的特性，因此后续加速能力略高。

图5 不同界面位置下弹丸底部的压力对比Fig.5 Pressure-time histories of launchers with different initial gas interfaces

3.3 计算结果与单一氦气驱动对比

当采用单一氦气作为驱动气体时，仅考虑冲击波第1 次与弹丸的相互作用，此时可将公式(14)简化为：

式中：带下标12 的量是指气体冲击波与弹丸作用后区域的参数。利用式（15）对表1 中的状态进行计算，通过调整充气压力使得发射过载pb,max（即pb最大值）或发射速度ub与式(14)结果相同，获得的相同过载时的发射速度和相同发射速度时的过载分别如图6～7 所示，图中横坐标n为与表1 中对应的算例编号。可以看到，在相同过载pb,max下，采用梯度气体获得的弹丸速度比采用单一氦气获得的速度高0.4～1.4 km/s；在相同发射速度下，采用梯度气体可降低发射过载0.2～0.9 GPa。说明采用梯度气体代替单一气体驱动能够有效提升发射速度或降低发射过载。

图6 发射速度结果与单一氦气驱动对比（相同过载）Fig.6 Muzzle velocities compared with the launchers with only helium driven gas (under the same pb,max)

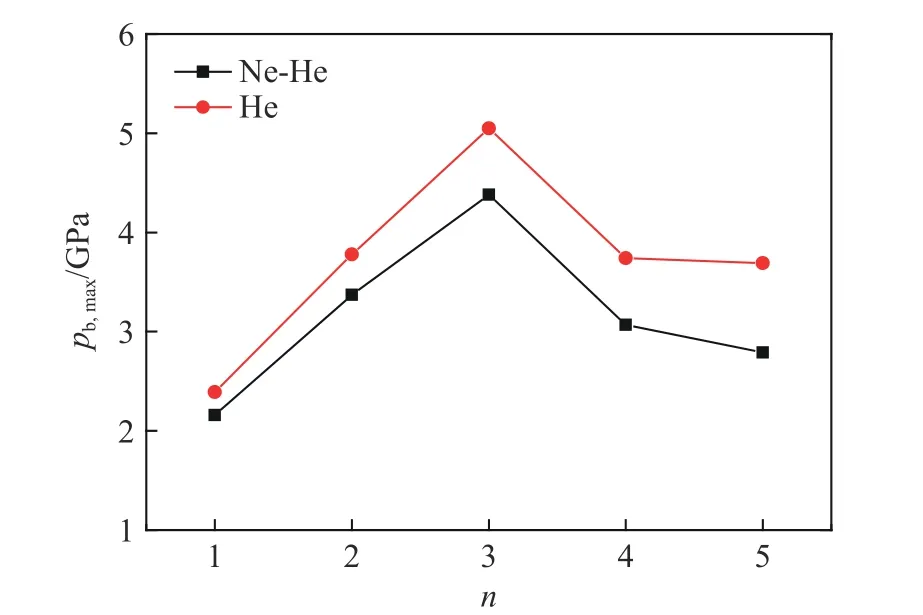
图7 发射过载结果与单一氦气驱动对比（相同过载）Fig.7 Maximum base pressures compared with the launchers with only helium driven gas (under the same ub)

4 发射速度、弹底压力影响参数分析

可能影响弹丸发射结果的因素有气体1 的类型、活塞运动的距离Lpist/(L1+L2)、活塞速度D、初始填充压力、界面初始位置等。其中气体1 的类型不同主要体现在气体的密度和多方气体指数两个参数。下面分别利用公式(14)对不同状态下弹丸的发射速度和最大弹底压力进行计算，分析上述因素对弹丸两种发射参数的影响程度。

4.1 初始填充压力与界面位置

以Ne 作为气体1、活塞运动距离Lpist/(L1+L2)=80%、活塞恒定运动速度D=7 km/s 为基础，改变初始填充压力和界面初始位置，计算得到的弹丸发射速度和弹底最高压力分别如图8～9 所示。从图中可以看出，发射速度随界面位置的变化不明显，但随填充压力的增大而迅速增大；最大弹底压力随界面位置和填充压力的增大而均显著增大。最大弹底压力随界面位置增大显著增大的原因是，界面位置越大意味着界面与弹丸之间的距离越小，造成二次压缩波到达弹丸底部的时间更短，两次冲击波强度叠加后的强度增强，最终使得弹底压力增大。

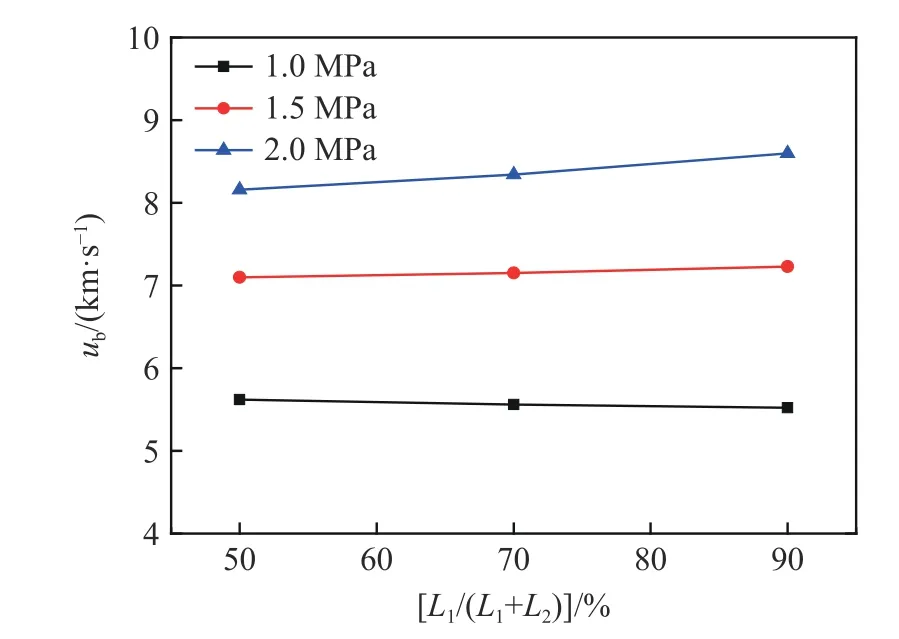
图8 界面位置和初始填充压力对速度的影响Fig.8 Muzzle velocities of launchers with different initial pressure and position of gas interface

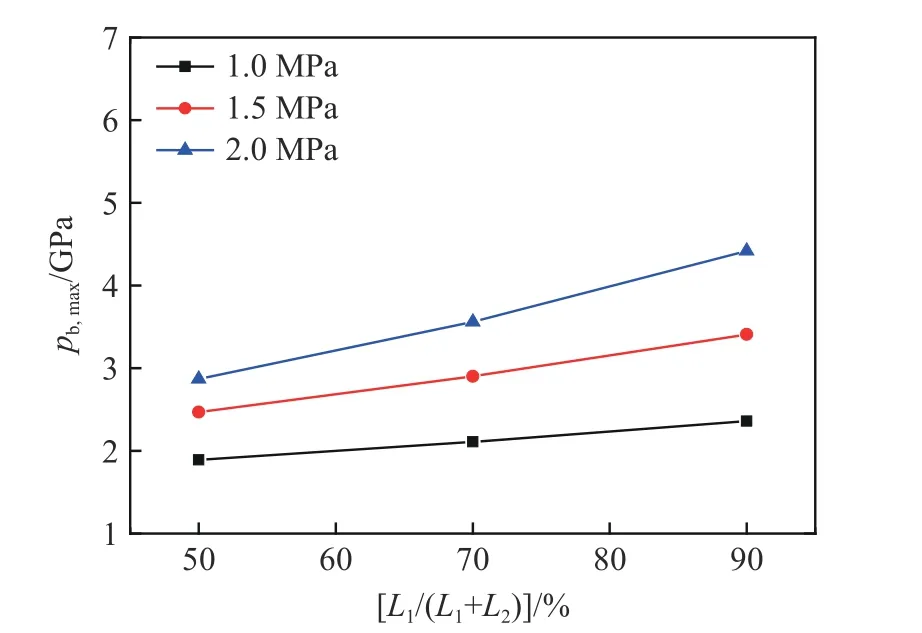
图9 界面位置和初始填充压力对过载的影响Fig.9 Maximum base pressures of launchers with different initial pressure and position of gas interface

4.2 活塞运动距离与速度

仍以Ne 作为气体1，设置填充压力为2.0 MPa、界面位置L1/(L1+L2)=70%，改变活塞运动距离与速度，计算结果如图10～11 所示。可以看到，发射速度和最大弹底压力均随活塞速度的增大而近似线性增大，这是由于活塞运动速度的增大使得冲击波强度增强，从而提升了弹底压力。随着活塞运动距离的增大，发射速度也会增大，但最大弹底压力却几乎不变。这是由于活塞运动距离仅影响活塞的终止时间，运动距离越大，活塞运动时间也越长，稀疏波追赶上弹丸的时间也越长，从而使弹底保持高压的时间也越长，发射速度也就越大；而最大弹底压力是由二次冲击加载形成的，与活塞运动距离造成的稀疏波的追赶时间无关。

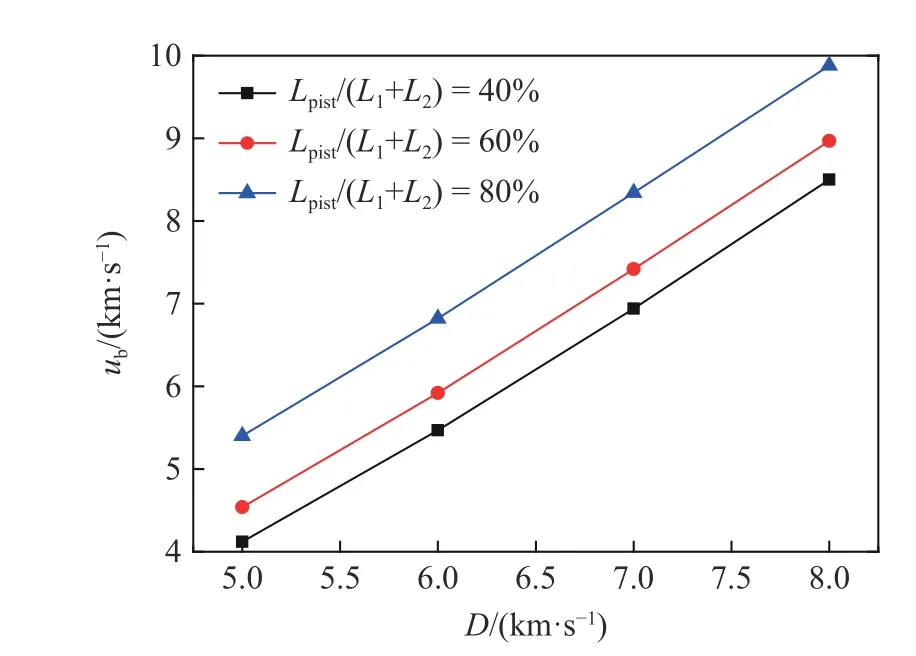
图10 活塞运动距离与活塞速度对速度的影响Fig.10 Muzzle velocities of launchers with different D and displacement of the piston

图11 活塞运动距离与活塞速度对过载的影响Fig.11 Maximum base pressures of launchers with different D and displacement of the piston

4.3 气体1 的密度和多方气体指数

设置填充压力为2.0 MPa、界面位置L1/(L1+L2)=70%、活塞运动速度为7 km/s、活塞运动距离Lpist/(L1+L2)=80%、气体2 为Ne，改变气体1 的密度ρ10和多方气体指数γ1。为便于对比，气体1 的 密度以Ne 的密度为基数，以相对密度形式变化，即同等压力下Ne 的相对密度为1.0。计算结果如图12～13 所示。从图中可以看到，随着多方气体指数的增大，弹底压力逐渐减小；而发射速度随气体相对密度的增大而增大，且随多方气体指数的增大发射速度的增幅也会变大。因此，气体1 应选择多方气体指数和密度较大的气体，如Ne、Ar 等。

图12 气体1 参数对速度的影响Fig.12 Muzzle velocities of launchers with different ρ10 and γ1

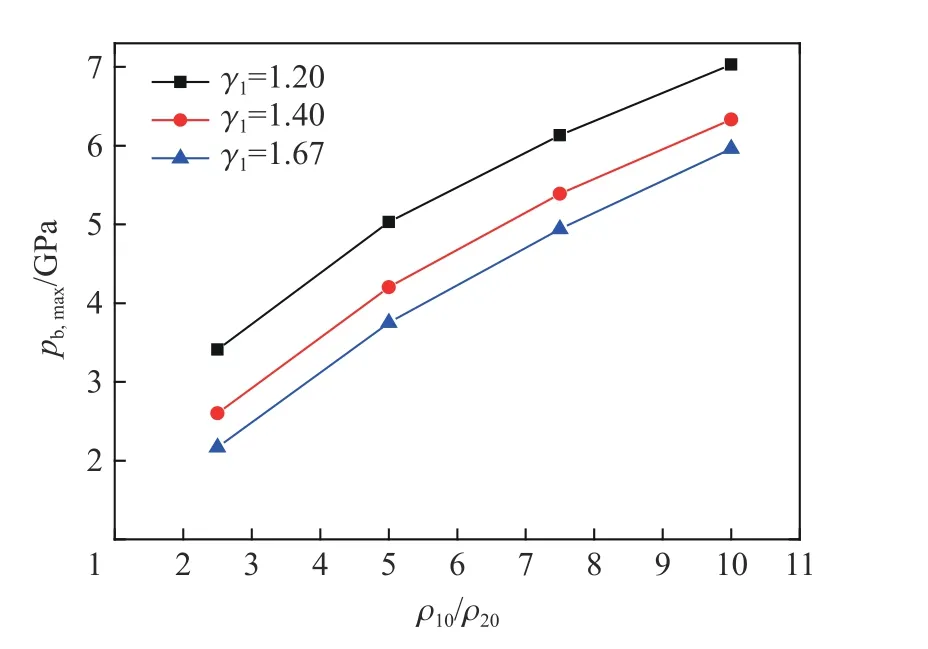
图13 气体1 参数对过载的影响Fig.13 Maximum base pressures of launchers with different ρ10 and γ1

4.4 各参数敏感性分析

对比图8～13，在所计算的参数范围内，各参数的变化对发射速度和过载的影响如表2 所示。从表中可以看出，气体压力的变化（1～2 MPa）能够将发射速度提升2.54～3.08 km/s、发射过载提高0.98～2.06 GPa；界面位置变化（50%～90%）可使发射速度提升不超过0.5 km/s、发射过载提高0.47～1.55 GPa；活塞运动距离变化（40%～80%）可使发射速度提升1.28～1.4 km/s，但发射过载几乎不变；活塞运动速度变化（5～8 km/s）可使发射速度提升4.38～4.48 km/s、发射过载提高2.85 GPa；高密度气体的密度变化（（2.5～10）倍低密度气体的密度）可使发射速度提升4.08～6.02 km/s、发射过载提高3.62～3.79 GPa；高密度气体多方气体指数的变化（1.2～1.67）可使发射速度提升-0.14～1.80 km/s、发射过载降低1.24～1.07 GPa。从以上分析可知，发射速度对气体密度和活塞运动速度最敏感，气体压力次之，再次为多方气体指数和活塞运动距离，对界面位置最不敏感；发射过载也对气体密度和活塞运动速度最敏感，其次为气体压力、界面位置和多方气体指数，对活塞运动距离不敏感。

表2 发射能力对各参数的敏感性分析Table 2 The sensitivity of parameters in affecting launch performance

从以上对各参数的定性和定量分析可以看出，要提高发射器的发射速度，气体1 应选择多方指数和密度较大的气体、活塞速度和运动距离越大越好，气体界面初始位置应在保证能够实现二次冲击加载的前提下尽量小、填充气体压力越大越好。

5 结 论

对双气体填充的等直径发射器建立了理论求解模型，采用理论模型对发射器的结构和装填参数进行了分析，获得了发射速度和最大弹底压力随气体1 的密度和多方气体指数、气体界面位置、活塞运动速度和距离、初始压力等的变化规律。获得以下主要结论：

(1)提出了一种采用梯度气体替代单一气体驱动的方式，并建立了双气体驱动理论求解模型，与有限元仿真获得的加速过程和发射速度结果吻合，发射速度误差不超过8.1%；

(2)通过对比采用单质氦气和梯度气体作为驱动气体时弹丸的发射速度和发射过载，发现采用梯度气体作为发射器的驱动气体能够有效降低发射过载、提升发射速度；

(3)气体密度和活塞运动速度对发射速度和过载的影响最大，其次为气体压力和多方气体指数，在设计等直径梯度气体驱动发射器时，应当选择多方气体指数较高的气体作为高密度气体，活塞速度和运动距离尽可能大。

感谢加拿大麦吉尔大学Andrew Higgins 教授就本文中梯度气体的驱动方法进行的有益讨论与指导！