神经网络状态方程在强爆炸冲击波数值模拟中的应用*

李秦超，姚成宝，程 帅，张德志，刘文祥

（西北核技术研究所，陕西 西安 710024）

数值模拟是分析爆炸力学现象的重要手段之一，目前普通爆炸的数值模拟方法相对成熟[1]，计算可靠性较好。强爆炸数值模拟方法与普通化学爆炸数值模拟方法的主要区别体现在爆炸产物状态方程（equation of state, EOS）上，状态方程的准确性是决定强爆炸数值模拟结果可靠性的关键。

强爆炸产物的初始状态非常极端，参数跨度范围特别大。目前常用的JWL、BKW 等状态方程均是基于单一方程形式的半经验或经验公式[2]，此类状态方程在强爆炸产物状态参数跨度下维持适用性显然较为勉强。神经网络具有强大的非线性逼近能力，能够处理复杂的多维、非线性问题，因此在材料本构模型及仿真等方面具有广泛的应用。1990 年，Ghaboussi 等[3]首次提出使用神经网络建立复杂材料本构模型来代替传统数学方程，后来学者们围绕该课题开展了广泛的应用研究，例如：Sungmoon 等[4]使用自进步神经网络建立率相关材料本构模型；曹吉星[5]使用遗传神经网络生成混凝土的本构模型并进行了有限元仿真；何龙等[6]建立了基于BP 神经网络的高温合金本构模型，并能准确地预测合金高温流变应力；崔浩等[7]提出了一种利用BP 神经网络-遗传算法和冲击Hugoniot 关系来确定未反应炸药JWL 状态方程参数的方法。从理论上来说，神经网络在强爆炸产物状态方程上具有很大的应用潜力，但目前将神经网络应用于强爆炸产物状态方程的研究极少。

本文应用BP（back propagation）神经网络学习强爆炸产物状态的数据库，得到神经网络状态方程的显式表达，并将神经网络植入到爆炸冲击波数值模拟程序中，求解与参考数据相吻合的强爆炸冲击波参数，以探索将神经网络状态方程应用于强爆炸冲击波数值模拟的可行性。

1 基于机器学习的强爆炸产物状态方程

1.1 神经网络状态方程

由于实际的强爆炸装置材料组成较为复杂，选取合适的等效方式进行处理能够使问题简化，乔登江[8]提出使用铁蒸气的参数进行强爆炸流体动力学的数值模拟，应用Saha 电离平衡理论求解铁蒸气的状态参数，并归纳为数值表形式的状态方程，数值计算时通过双线性插值的方法进行查询、计算，所得结果与实际比较符合。

传统插值方法形式直观，但是数据样本无规律时，插值将极其复杂，且插值算法对数据具有一对一的针对性，无法泛化推广。此外，插值方法需要频繁的搜索、查询操作，在大规模数值计算时的计算效率不高。由于神经网络在处理高维、大样本的非线性数据库时具有算法高效、泛化能力强等优势，利用同一种神经网络算法，可以处理分布各异的数据样本，且数据样本越多，神经网络预测越精确，不存在计算效率与精度之间的对立矛盾。因此，利用神经网络来对存储物质状态参数的状态方程数据库进行数据的训练和驱动，将对提升状态方程的准确性和计算效率起到至关重要的作用。其中，强爆炸的铁蒸气等效神经网络状态方程概念如图1 所示，图中p为爆炸产物的压力，ρ 为产物的密度，e为产物的比内能。

图1 神经网络状态方程概念Fig.1 Conceptual sketch of equation of state using neural network

1.2 状态方程数据库

1.2.1 芝麻数据库

芝麻数据库（Sesame EOS data）[9-10]，由LASL（Los Alamos Science Laboratory）研制，是比较先进的状态方程数据库，其数据可以在很宽的密度和温度范围内，精确地表示密度、温度、压力以及能量之间的函数关系，相较于解析形式状态方程具有很强的普适性与先进性。库中包括铁蒸气的特性参数与EOS 数据，表1 截取了芝麻数据库中铁蒸气的部分数据，铁蒸气所有数据样本中密度的最大值达到157 kT·m-3，比内能最大值达到3 310.6 GJ·kg-1，压力最大值达到3.371 0 × 1020Pa。

表1 芝麻数据库中铁蒸气数据（部分）Table 1 Iron steam data in sesame data(part)

1.2.2 数据预处理

芝麻数据库的数据范围广、应用场景广，可应对多种工况，乃至极端工况下的物质状态，但同时也为数据处理带来了极大的困难。由于数据跨度极大，且数据点分散，数据在线性空间分布极不均匀，对后续神经网络进行数据学习提出了很大的挑战。

为解决上述问题，在数据集方面，对3 类数据变量（密度ρ、比内能e、压力p）进行预处理，具体步骤如下。

(1) 对数变换—对三类变量均取对数，将线性空间内的分布状态转化至对数空间。

(2) 去噪—将数据噪点、边缘毛刺样本去除，提升样本光滑度。

(3) 归一化—将大跨度的数据整合至[-1, 1]区间内，提升神经网络预测精度，采用下式对数据进行归一化处理：

式中：为第i个未归一化处理的值，Ki为其经过归一化后的值，Kmax和Kmin分别对应于数据集中的最大值和最小值。

预处理前后样本分布情况具有直观的对比。图2(a)为以铁蒸气的密度、比内能为横轴、压力值为纵轴的原始样本分布散点图，可以看出样本分布极不均匀。由于纵轴压力值的数量级跨度极大，导致小数量级的散点在视觉上产生聚集。图2(b)为经过预处理后的散点图，其中 ¯ρ、e¯ 和p¯ 为经过归一化的值。样本曲线拟合近似线性，样本分布均匀且光滑，在数据集上能够满足对神经网络训练样本的需求。

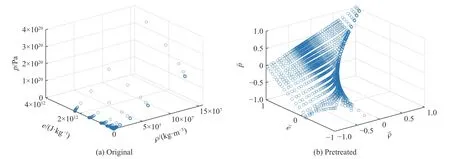
图2 数据样本散点图Fig.2 Data sample scatter plot

1.3 神经网络的搭建与训练

1.3.1 BP 神经网络

BP 神经网络是经典的机器学习算法，具有结构简单、非线性能力强等优点，在提出多隐含层的网络结构后，成为深度学习的重要算法之一。采用BP 神经网络生成状态方程模块，假设神经网络的隐含层数为L，每一层上的节点数均为N，则神经网络的参数结构如图3 所示。

图3 神经网络参数结构Fig.3 Neural network parameter structure

神经网络层数与节点数受到具体问题与数据集的约束，一般来说，训练样本数应为总权数的2～10 倍[11]。可根据“2 倍原则”来确定神经网络的理论单层最大节点数，本文的训练样本数S= 2 202，神经网络权值的总个数MW和阈值的总个数Mb以及其应当满足的约束关系分别为

计算得到的理论最大节点数见表2。

表2 不同隐含层数量对应的理论单层最大节点数Table 2 The number of the maximum nodes of single layer

BP 神经网络的特点是误差反向传播，训练步骤主要分为4 步：(1) 信息正向传播，计算神经网络前向传播值；(2) 误差逆向传播，计算神经网络误差函数的反向传播值；(3) 更新权值阈值，该过程使用近似的梯度下降法；(4) 重复以上三步，交替进行正向传播与逆向传播，不断对神经网络权值与阈值进行更新，当达到设定目标时，训练终止。本文在神经网络状态方程训练过程中选用的误差函数为均方误差（mean squared error,MSE），神经网络状态方程建立过程的主要步骤如图4 所示，图中上方虚线框内为训练集生成和神经网络初始化过程，下方虚线框内为神经网络训练过程。

图4 神经网络状态方程建立过程Fig.4 Establishment process of equation of state using neural network

1.3.2 神经网络结构优化

结构优化的最终的目的是选取均方误差较小且结构较简单的神经网络结构，进而提升该状态方程模型的计算精度和效率，最终提升后续数值模拟的计算精度和效率。依据图4 中的流程，在神经网络初始化阶段设置不同的L和N，对比测试其训练完成后的MSE 大小，值越小则拟合精度越高，则神经网络拟合误差参量可定义为MSE 的大小。由于神经网络的初始权值阈值的随机性，同一种结构的测试结果也不尽相同，为避免偶然性，对每种结构分别进行6 次测试，去除MSE 最大值和最小值后剩余4 个值作为有效结果，分别记为δ1、δ2、δ3、δ4，将δ1、δ2、δ3、δ4的平均值记为δ，见表3，其中最大节点数的选取参考表2。

表3 神经网络结构测试均方误差Table 3 Mean squared error of different Neural network structure

当实际节点数量达到理论单层最大节点数时，神经网络可能出现误差放大，也可能出现输出精度的跳跃，即同一种结构神经网络多次训练结果差异较大，这反映了该神经网络的训练过程不够稳定。在神经网络的预测误差差距不大的情况下，优先选择结构更简单、权值数量更少的神经网络。表中共有5 种神经网络结构的平均预测均方误差小于1.2×10-5，其中4 层10 节点网络结构相对简单，因此选择该网络结构，如图5 所示。

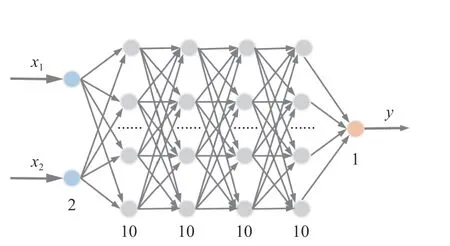
图5 神经网络结构Fig.5 Neural network structure

该模型在神经网络训练过程中均方误差大小δ 随迭代次数n的变化如图6 所示，蓝色实线为训练集表现，绿色实线为验证集表现，红色实线为测试集表现，在迭代至323 步时神经网络获得最优验证集表现并且在图中采用虚线及圆圈对其进行了标识。迭代过程中误差曲线下降较为平滑，表明训练过程稳定收敛。

图6 神经网络训练表现Fig.6 Neural network training performance

由此已经获得了能够预测强爆炸产物压力值的神经网络状态方程模型，其具有4 个隐含层，每个隐含层均具有10 个神经元节点，下面将继续介绍如何应用该模型进行准确性验证。

2 神经网络与数值计算的融合

由于神经网络“黑箱”般的复杂结构，必然导致神经网络状态方程模型具有较为繁杂的运算过程和参数组成。本节将通过分析神经网络状态方程的算法结构，给出其具体的数学表达式和参数，为将其植入数值计算程序提供依据，并简要介绍了所采用的数值计算方法。

2.1 神经网络状态方程的显式表达

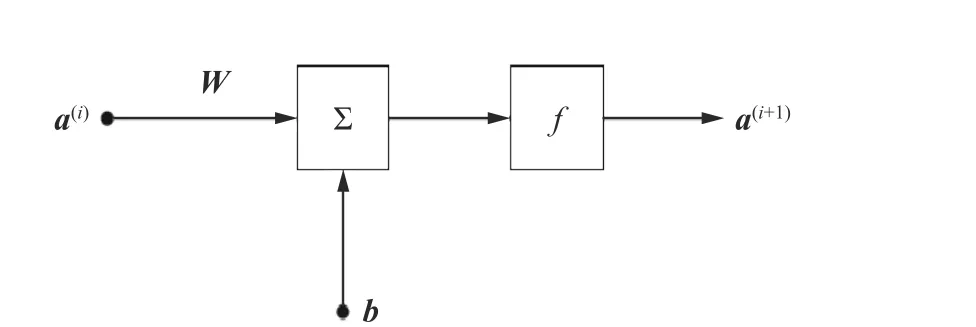
神经网络状态方程的整体运算结构见图7，图中首尾正方形代表输入输出，矩形代表层结构，其中Layer 5 为输出层，其余为4 个隐含层，圆圈代表各层之间的数据交互，a代表前向传播的数据（即中间变量），是层与层的中间变量，右上角括号内数字代表神经网络层数。图8 为第i个层结构的内部运算结构，其中W代表权值，b代表阈值，f为激活函数，其余隐含层的结构也是类似的。

图7 神经网络整体运算结构Fig.7 The overall operational structure of neural network

图8 中f代表的激活函数包括线性函数（y=x）和双曲正切函数（y=tanhx）等，其中x为函数输入，y为函数输出。神经网络的运算参数组成如表4所示，其中，各数值仅代表参数数量，数据结构“10×2”代表10 行2 列的矩阵，该神经网络有330 个权值，以及41 个阈值，一共371 个参数值。

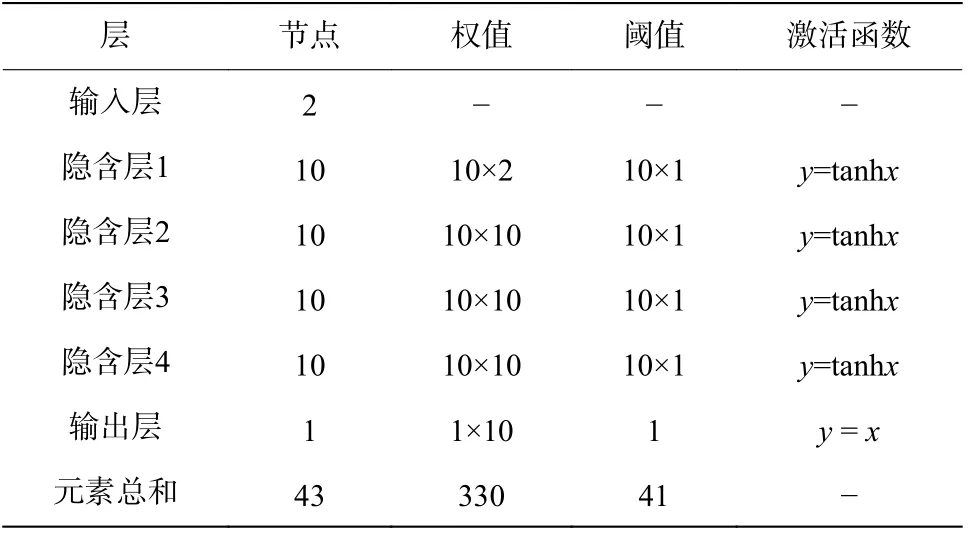
表4 神经网络参数组成Table 4 Neural network parameter composition

在第i个隐含层，信息向前传递的方式为：

根据式(5)，神经网络状态方程p=fn(ρ,e) 可由如下步骤的表达式表示：

式中：第1 步为输入值的对数变换及归一化，第2～5 步为神经网络隐含层计算，第6 步为神经网络输出层计算，第7 步为输出值的反归一化和反对数变换；密度ρ、比内能e为神经网络的输入；压力p为神经网络的输出，p为归一化的压力值；a为中间变量矩阵，由每步计算得出；右上角括号内数字代表神经网络层数，例如W(1)代表神经网络第一隐含层的权值矩阵；系数k、c为归一化（或反归一化）系数。至此，神经网络状态方程模型的运算表达式已经得到完整描述，其归一化系数kρ= 0.135 542，ke= 0.091 564 7，kp=14.702 6，cρ= -0.621 631，ce= 0.047 042 8，cp= 7.235 89，权值矩阵和阈值矩阵参数数量庞大，此处不再赘述。

2.2 数值计算

根据预处理数据集优化后的数据范围，以及神经网络实际测试效果，结合实际工况应用需求，确定了神经网络状态方程的应用范围，即密度大于等于61.33 kg·m-3，比内能大于等于20 MJ·kg-1。

神经网络状态方程应用的工况范围对应于强爆炸前期距爆心较近的核心区域的强爆炸产物，具有较高的密度与比内能，其余工况对应于常规区域内压力处于常规范围的爆炸产物，此时使用经典的理想气体状态方程即可，具体见下式：

式中：γ = 1.4 为理想气体绝热指数。数值计算过程中对爆炸产物的压力计算方法依据上式进行。

爆炸冲击波数值模拟的控制方程采用一维球对称形式的Euler 方程组：

式中：u为速度；r为距离；E为单位体积的总能量，且满足E=ρe+ρu2/2。

采用有限体积方法对式(8)进行数值离散，其中空间方向利用local Lax-Friedrich 数值通量函数来计算单元边界上的数值通量，时间方向采用向前Euler 方法进行数值离散。详细的数值求解过程请参考文献[12]，此处不再赘述。

3 数值算例与验证

3.1 神经网络验证

对神经网络输出性能的评价，主要从输出的相对误差大小、是否过拟合等方面判断。神经网络模型对训练集的输出误差小，说明神经网络预测精准，很好地发挥了拟合作用；神经网络对未知的测试集也有良好的精度，说明未发生过拟合，泛化性能优秀。

3.1.1 预测精度

对训练集进行验证，训练集由满足2.2 节中神经网络状态方程应用范围内的训练样本组成。图9 对比了神经网络的预测输出与原始样本，可直观地看出，几乎所有代表预测值的点均精准地落在了代表原始样本点的空心圆之中。神经网络对训练集的输出相对误差随输入变量的分布见图10，拟合的最大相对误差为10.89%，最小相对误差为0.000 97%，平均相对误差为0.75%，计算结果表明神经网络对训练集的表现良好。

图9 训练集检测拟合精度Fig.9 Fitting accuracy of training set

图10 神经网络压力输出相对误差Fig.10 Relative error of pressure output value of neural network

3.1.2 过拟合检测

将训练集插值处理形成测试集，测试集更加密集，包含神经网络未学习训练过的数据。测试结果如图11 所示，点代表测试输出，三角形代表原始样本，较密集的测试输出平滑地镶嵌于较稀疏的原始样本间，没有产生明显的波动与偏离，神经网络对测试集的表现良好，未发生过拟合现象。

3.2 数值算例

3.2.1 初始工况

一般情况下，爆炸装置的实际物理结构为球形结构，球体半径大小变化不大，而质量会随当量发生变化，选取强爆炸当量为15 kt TNT，参考相关文献[13-15]大致确定其初始质量与初始半径，进一步换算得到爆炸产物的初始密度与初始比内能。爆炸装置的具体初始参数见表5。

表5 装置初始参数Table 5 Initial device parameter

计算表中装置起爆后产生的强爆炸冲击波参数。计算的物理时间为0.5 s，物理空间为410 m，假设爆炸在标准大气压下的空中自由场中发生，忽略所有障碍物与地面。

3.2.2 结果分析

在时间t为爆后166 ms 时爆炸流场随爆心距r的分布如图12 所示，在离爆心距离r为100 m 的位置处冲击波参数随时间t变化的曲线如图13 所示。

图12 爆后166 ms 爆炸流场分布Fig.12 Explosive flow field distribution at 166 ms after the explosion

图13 爆炸流场历程曲线Fig.13 Explosive flow field history curve

以比距离为横坐标，分别对峰值超压、冲击波到时的计算值进行验证，参考值来自相应的经验公式[16]，结果如图14 所示。可以发现，数值计算结果与参考值曲线符合较好，部分观察点极为接近。选取不同爆心距的4 个点位，计算其数值计算与标准结果的相对误差，结果见表6。爆心距大于200 m 后的峰值超压计算值偏大，但是总体来看，数值计算的相对误差大多数能控制在15%以下。

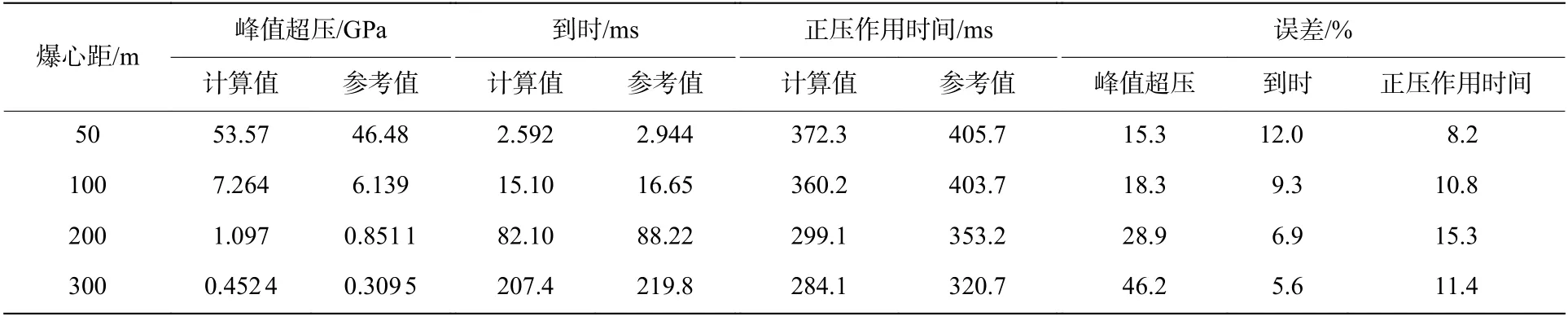
表6 数值计算误差Table 6 Error of numerical simulation

图14 数值计算结果对比Fig.14 Comparison of numerical results

4 结 语

强爆炸产物的状态方程是非线性模型，其参数范围跨度大、非线性程度高，状态方程数据库中的热力学数据能够较为准确地描述产物的热力学状态。神经网络具有强大的非线性拟合能力，基于大量的热力学数据，能够建立起复杂的映射关系从而表征强爆炸产物的状态方程关系。神经网络状态方程模型具有拟合精度高、未过拟合、可快速调用的优点，可以作为状态方程的优化方案从而取代传统状态方程，应用于数值模拟程序之中。现有的计算结果表明，神经网络状态方程计算获得的强爆炸冲击波结果与标准结果的一致性较好，该方法具有一定的应用价值。