关注“构造思想”在解题中的活用
张文景
江苏省常熟市浒浦高级中学
数学中的“构造思想”,是指在观察、分析的基础上,灵活构造适当的数学模型,进而找出解决问题的方法,其具有直观性、灵活性、构造性、可行性和思维的多样性等特点.在解题教学中,有意识地加强学生对“构造思想”的理解与运用,不仅有利于提高学生的数学学习能力,而且有利于拓展学生的数学思维能力[1].
1 构造等差数列,巧解题
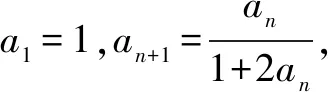
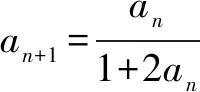
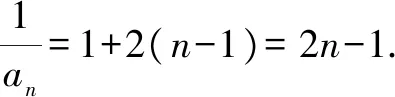

评注:本题求解关键在于三点.一是对数列递推式“取倒数”变形;二是根据等差数列的定义,灵活构造等差数列;三是灵活运用等差数列的通项公式,巧解题.
2 构造等比数列,巧解题
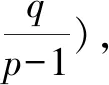
例2已知数列{an}中,a1=1,an=2an-1+3(n≥2,且n∈N*),求an.
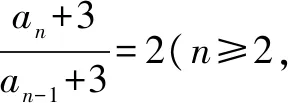
于是,数列{an+3}是首项为4,且公比为2的等比数列.
所以,可得an+3=4·2n-1=2n+1.
故所求an=2n+1-3.
评注:上述求解的关键是先利用“同加”变形,构造等比数列;再灵活运用等比数列的通项公式,巧解题.
3 构造函数,巧解题
处理函数与不等式的交汇问题时,若题设中给出了与导数有关的不等式,则往往需要考虑导数的运算法则,先灵活构造新函数,再根据新函数的单调性加以巧解.
例3已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x) A.f(2)>e2f(0),f(100) B.f(2) C.f(2)>e2f(0),f(100)>e100f(0) D.f(2) 从而,可得f(2)>e2f(0),f(100)>e100f(0). 故答案选C. 评注:从目标问题出发,通过观察各选项所给不等式的外在结构特点,很容易想到构造函数,进而灵活运用函数的单调性解决问题. 评注:上述解法中需关注两点:一是如何根据函数表达式,灵活构造向量;二是利用向量不等式求解最值问题时,必须具体考查不等式取等号的条件是什么. 处理有关解三角形的问题时,我们往往关心的是正、余弦定理在解题中的灵活运用.实际上,有不少这样的解三角形问题,往往可通过构造直角三角形巧妙获解[2]. 图1 评注:①结合AB=AC或∠ADC=45°,本题应作BC边上的高;②本题如果不作辅助线,则应综合运用正、余弦定理解题,整个过程相对较繁! 一般地,设d表示圆心到直线的距离,r表示圆的半径,则直线与圆有公共点(即相切或相交)⟺d≤r.灵活运用这一结论,可顺利解决许多貌似与直线和圆无关的数学问题,往往巧妙之极,真的令人拍案叫绝! 例6(2014·浙江卷)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是______. 评注:本题结合直线方程ax+by+c=0和圆的标准方程(x-a)2+(y-b)2=r2的外在结构特征,很容易想到利用已知方程的几何意义,去构造直线和圆,巧解题. 由于长方体和正方体是特殊的立体图形,它们均具有许多特殊的性质,所以分析、解决有关三棱锥(即四面体)的问题时,往往可通过构造长方体或正方体加以巧妙求解. 图2 不难发现,关注“构造思想”在解题中的灵活运用,有利于等价转化目标问题,有利于变换角度看透问题的本质,有利于培养学生在数学抽象方面的核心素养[3]!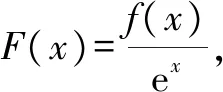
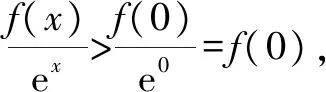
4 构造向量,巧解题
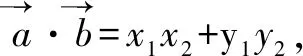

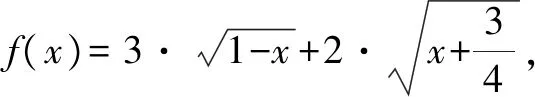
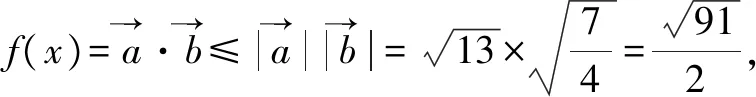
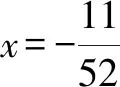
5 构造直角三角形,巧解题
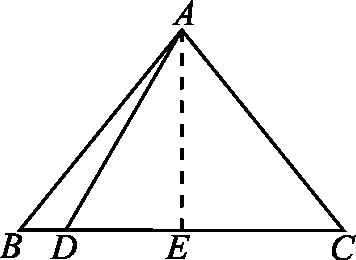
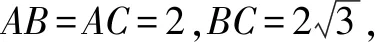
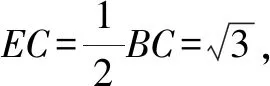

6 构造直线和圆,巧解题
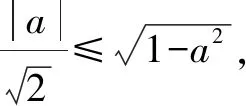
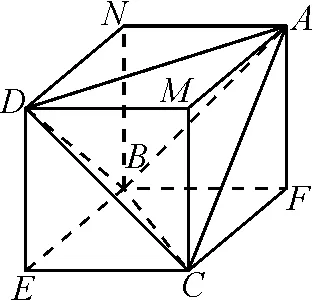
7 构造特殊的几何体,巧解题