基于风险的战略物资补充优化模型*

吕学志，刘玉梁，冯晓容

（陆军研究院，北京 100021）

0 引言

战略物资储备指为了应付战争和其他意外情况，保障国民经济正常运行和国防需求，国家在平时有计划建立的一定数量的重要物质资料储存或积蓄，是国家为了保障非常时期战略物资供应的一种重要方式［1］。

我国学者主要从理论分析角度对我国战略物资储备体系［2-4］、体制［5］、法规［6-7］进行定性研究，还有部分学者从量化分析角度对战略物资储备进行定量研究。曹丽认为应当根据未来“危态”下对于战略物资的需求趋势，以及对战略物资的动员能力等，合理确定储备量和动员量，保障“危态”下战略物资供给，优化战略物资的储备规模。但是并没有建立量化模型，只是进行了定性分析［8］。杨凯等基于系统动力学原理和方法，建立了战略物资储备控制系统动力学仿真模型，分析了不同要素对战略物资储备控制的影响［9］。张永领在综合考虑影响应急物资储备的主要因素的基础上，将应急物资分5类；界定了3 类应急物资储备方式；采用层次分析法对应急物资的储备方式进行了研究［10］。包玉梅以政府为本位，以应急反应绩效和应急成本为约束条件，研究在应急预案、应急物资储备管理制度和应急物资储备策略这3 个维度的政府应急效用最大化，并建立了理论模型［11］。

由于涉及国家机密，国外在国家战略物资储备方面公之于众的研究成果也很少。综观美国、日本、德国等发达国家对于国家战略物资储备相关问题的研究，他们普遍非常重视战略物资储备，经过多年的不断发展，其战略物资储备体系在法律制度上、储备规模上、储备方式上已基本完善。特别是美国政府早在20 世纪70 年代以来，就根据目标设计来确定物资收储，目标不同，储存品种也随之变化。由此建立优化模型，权衡储备的费用和收益，并设立指标体系，评价投入产出的比值。该评价体系的建立，弥补了政府对各类储备的费用收益分析的空白，尽管不尽完美，但对美国的政府储备的计划、采购、收储、动用都进行了量化，储备目标更加明确，非常值得学习和借鉴。文献［12］建立了战略物资的动态规模模型。文献［13］提出了一种在各种供需条件下确定战略石油储备（SPR）的最佳规模、补充和动用率的模型。文献［14］介绍了用于确定公司采购策略的信息系统。文献［15］提出了一种在军队内部权衡费效比、优化战略物资储备的模型。

本文提出的优化模型是为了优化完善国家战略物资风险管理，在一定费用和风险约束的范围内，得到最具效费比的战略物资补充方案。该模型不同于传统的战略物资储备规划过程，即估计战略物资缺口，并对获取和储存战略物资数量给出建议，转向一种基于风险的战略物资补充优化过程，以最小化战略物资的剩余短缺风险。同时模型考虑了战争可能性、战略物资短缺严重程度、成功补充的可能性，以及决策者风险偏好。

1 问题描述

本文考虑的战略物资补充优化问题是一个风险-费用权衡问题，即在费用和风险约束条件，找到最小化战略物资短缺期望总风险的战略物资补充组合方案。在管理战略物资短缺风险的过程中，考虑多种补充方式，其与传统储备在降低风险和成本方面的有效性不同。因此，在针对可能的规划场景制定优化方案时，必须估计和考虑到不同补充方式的费用，及其降低风险的效力。

1.1 补充方式

考虑5 种战略物资补充方式，作为弥补战略物资缺口的选项：

1）循环储备。国家购买和储存战略物资，保证国家国民经济按比例协调发展和应付战争、自然灾害等可能遭到的意外困难；储备的战略物资可以出售，一旦不再需要，其费用就可以收回，补偿预算费用。

2）缓冲库存。国家与物资供应商或制造商签订合同，令其存储一定数量的战略物资；国家将在需要战略物资的时候，支付租金和采购费用。

3）出口限制。国家作出政策决定，在紧急情况下限制该类战略物资及其相关产品的出口，优先确保国内物资供应。可能需要支付无法完成出口合同的违约金。

4）替代。使用其他物资或产品替代该类战略物资。

5）紧急购买。在战争和自然灾害等非常时期，国家在国内外市场紧急购买该类战略物资（价格可能较高）。

通过根据战略物资补充方式的能力、成功可能性和预期费用，确定建议使用哪些战略物资补充方式，并确定在何种程度上弥补战略物资的缺口。

1.2 风险度量

传统的战略物资储备规划过程为估算缺口，按照缺口估算量进行补充。本文采用一种基于风险的过程，即评估采用多种补充方式后的战略物资短缺风险，获得最佳的补充方案以减少这种风险。为此，首先必须定义用于优化模型的风险。风险的衡量标准如下：

平均风险= 初始缺口风险×平均剩余缺口风险因子

其中，初始缺口风险=战争概率×短缺严重程度。

战争概率是造成战略物资短缺的战争每年发生的概率；短缺严重程度是由专家根据一定的评价标准进行打分。

平均剩余缺口风险因子=平均剩余缺口/初始缺口

平均剩余缺口=初始缺口－补充方式带来的供应增加或需求减少；初始缺口是计划之前每种战略物资的短缺量。

1.3 补充费用

为评估总费用，为每一种补充方式设计了预期的净成本公式。虽然出口限制和替代从数学上讲是减少了战略物资需求，而不是增加战略物资供应，但是本文确实将其当作战略物资补充的来源。净成本对于循环储备尤其重要，因为它考虑了补偿，即在不再需要缓解短缺风险之后出售储备战略物资（假设在若干年的规划周期后进行补偿）。对缓冲库存、出口限制、替代和紧急购买来说，要使用期望费用，因为除非出现这种情况，否则通过这两种方式获得战略物资是不产生费用的。许多补充方式缓解战略物资短缺的能力是有限的，因此，即使是零成本，补充方式也不一定能够完全弥补战略物资的缺口。各种补充方式费用公式如下。

循环储备费用=（计划数量×单位价格）－（补偿率×补偿期贴现率×计划数量×单位价格）

补偿期贴现率=1/（（1+贴现率）补偿期长度-1）

贴现率适用于所有未来的成本和收益，具体描述公式为：现值=期值/（1+贴现率）期数。贴现率为10%，明年的100 块在今年就相当于100/（1+10%）=90.909 090...块钱，也就是说，今年用90.909 090...块可以买到的东西，相当于明年100 块可以买到的东西。

缓冲库存期望费用=（租金率×规划期限×平均贴现率×计划金额×单位价格）＋（战争概率×平均贴现率×成功概率×计划数量×单位价格）

平均贴现率=（1/规划期限）（（1+贴现率）0+...+（1+贴现率）规划期限-1）

出口限制期望费用=战争概率×平均贴现率×成功概率×计划数量×单位价格×（1+赔偿价格率）

赔偿价格率=单位违约金/单位价格

替代期望费用=战争概率×平均贴现率×成功概率×计划数量×单位价格×替代价格率

替代价格率=替代物资单位价格/单位价格

紧急购买期望费用= 战争概率× 平均贴现率× 成功概率× 计划数量× 单位价格× 战时价格率

2 建立模型

本文考虑的战略物资补充优化问题，本质上是希望用最小的代价换取最大的利益，而线性规划就是解决这类问题的一个重要方法，下面将介绍模型假设、变量和线性规划模型。

2.1 模型假设

模型的假设条件：

1）考虑|I|种战略物资，战略物资i 属于战略物资集合为I。对于每种战略物资有|J|种补充方式，补充方式j 属于补充方式集合J；j=1 表示循环储备；j=2 表示缓冲库存；j=3 表示出口限制；j=4 表示替代；j=5 表示紧急购买。

2）决策变量为·xij，表示通过补充方式j 提供的战略物资i 数量。

3）yij为通过补充方式j 提供战略物资i 的平均数量=Pijxij，其中，Pij为通过补充方式j 缓解战略物资i 短缺的成功概率；TYi为通过所有方式提供战略物资i 的平均数量=∑j∈Jyij。

5）不同类型补充方式之间没有相互作用，因此，它们的作用是可累加的。Ci1为战略物资i 通过储备方式补充的费用，其中，Qi为战略物资i 的单位价格为战略物资i 的补偿率为战略物资i 补偿期的贴现率，为战略物资i 的补偿期长度，即经过该时间段将战略物资按照一定补偿率进行出售。

Ci2为战略物资i 通过缓冲库存方式补充的期望费用，其中为战略物资i 缓冲库存租赁费用率，L 为规划期限，FAD为平均贴现率=（1/L）（（1+D）0+...+（1+D）L-1），PW为战争概率。

Ci3为战略物资i 通过出口限制方式补充的费用，其中：战略物资i 的赔偿价格率。Ci4为战略物资i 通过替代方式补充的费用

3 求解方法

由于战略物资补充优化模型是一个非线性规划模型，在极其特殊的条件下，才是线性规划模型。常规的解析求解法只适用于模型的几种特殊的情况，例如线性规划模型和二次规划模型。要想设计通用的模型求解算法需要利用智能求解算法。由于粒子群算法设计简单，适合求解连续优化问题，所以本文将采用粒子群算法对模型进行求解。

3.1 粒子的编码与初始化

粒子群中第l 个粒子可以表示为向量Xl（l=1，2，3，...，N），N 为粒子群规模，Xl=［Xl1，Xl2，…，Xl|I|］，粒子向量中的每个元素代表一种战略物资数量。

为了缩小粒子群算法求解空间，并减少迭代求解时间，将模型特殊情况下（∀Ei=1（i∈I））的线性规划模型解作为粒子群算法的初始解。可以使用MATLAB 中的linprog（）函数对模型特殊情况下的线性规模模型进行求解［16］。其使用方法：［x，fval］=linprog（f，A，b，Aeq，beq，lb，ub），用于求解以下模型：

其中，x 是决策变量向量；f 是目标函数向量；fval 表示最优解处的目标函数值；A 是不等式约束系数矩阵；b 是不等式约束常数向量；Aeq 是等式约束系数矩阵；beq 是等式约束常数向量；lb 和ub 分别表示决策变量的下界和上界，若不存在可以用空矩阵代替。本模型并不涉及等式约束，所以模型求解的关键是将模型中的参数构建linprog（）函数中的参数f、A、b、lb、ub。

3.2 适应度函数

计算粒子的适应度值

If 粒子满足约束（1～3）then

适应度f（Xl）为RT

Else

适应度值f（Xl）为inf

Endif

3.3 位置更新

4 应用示例

4.1 假设与数据

4.1.1 战略物资缺口数据

表1 列出了的初始缺口、初始缺口风险、价格、战时价格率、赔偿价格率、替代价格率等数据。

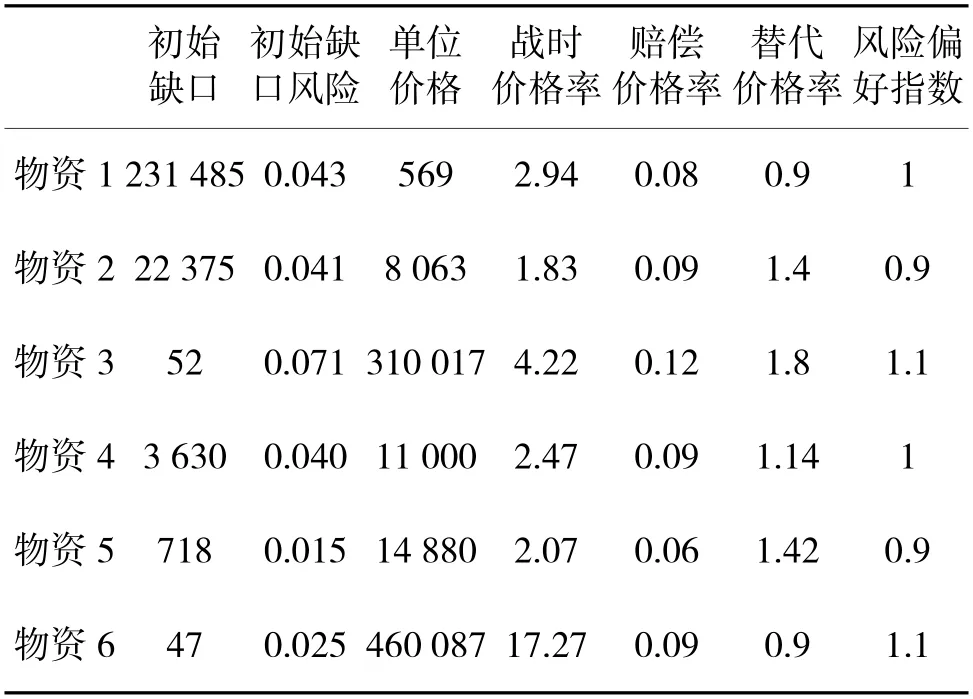
表1 战略物资缺口数据Table 1 Material shortfall data

4.1.2 规划假设与参数

战争概率PW=0.003 7

规划期限L=5 年

储备补偿率FR=0.84

缓冲库存租金率FBR=每年15%

假设事件发生在中期五年计划期间的贴现率，平均贴现率FAD=0.992，

补偿期的贴现率FRD=0.927

4.1.3 成功概率

每种战略物资5 种不同补充方式的成功概率（单位：%），如表2 所示。0 表示该战略物资的该种补充方式不可行。

表2 成功概率Table 2 Success probability

4.1.4 上限

每种战略物资不同补充方式的补充上限率如表3 所示（乘以初始缺口，即为变量xi1、xi2、xi3、xi4和xi5的上限）。

表3 补充上限率Table 3 Replenishment upper bound rate

平均总费用的上限CUB，示例中将取1 000 万元、2 000万元进行实验比较；战略物资i 的平均风险上限为战略物资i 初始风险的k 倍，示例中将取k=1、0.6、0.3 进行实验比较。

4.2 因素影响分析

粒子群算法控制参数为：N=40，M=40，1=0.5，2=0.5，ω=1。

4.2.1 费用和风险上限

表4 和表5 是当k=1～0.6、平均总费用的上限CUB=1 000 万时的优化方案、费用、效果，最小平均总风险为0.051 924，平均总费用达到极限1 000 万。

表4 优化方案（k=0.6，CUB=1 000 万）Table 4 Optimal solution（k=0.6，CUB=107）

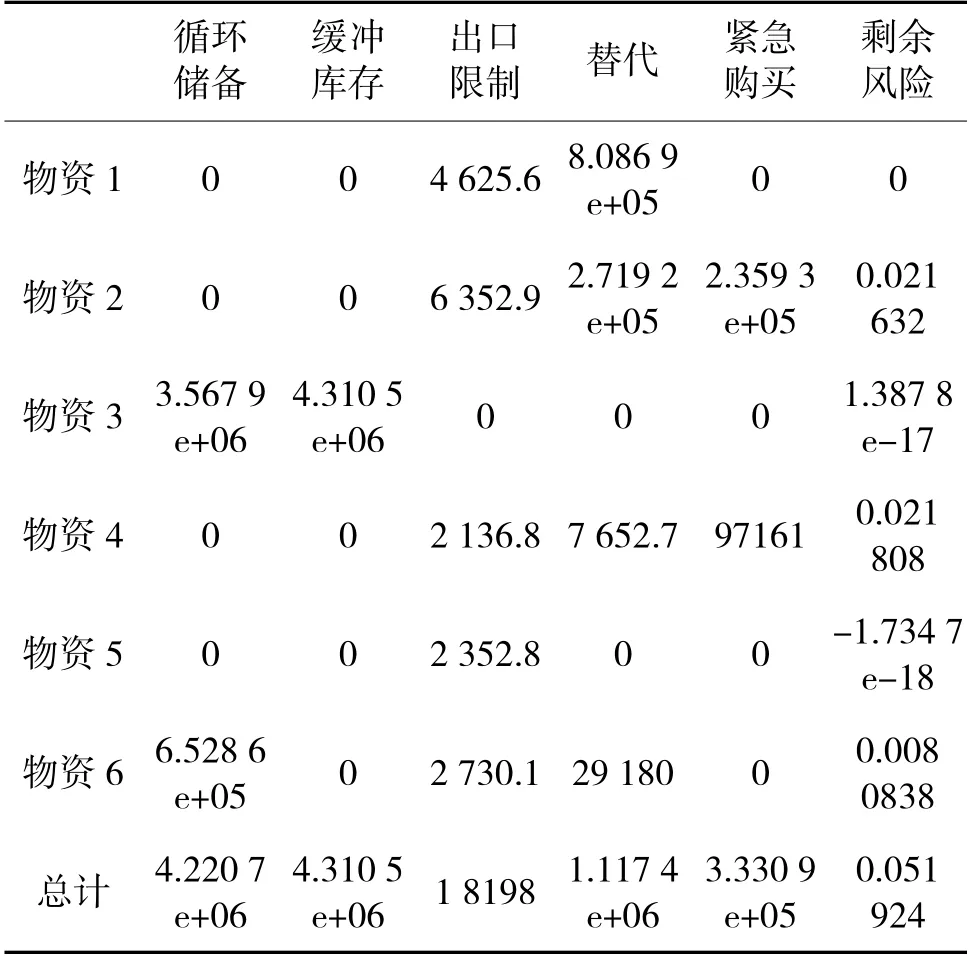
表5 方案费用和效果（k=0.6，CUB=1 000 万）Table 5 Cost and effect of solution（k=0.6，CUB=107）

表6 和表7 是当k=0.5、平均总费用的上限CUB=1 000 万时的优化方案、费用、效果，最小平均总风险为0.056 413，平均总费用达到极限1 000 万。当k＜0.5，则无法得到最优解。

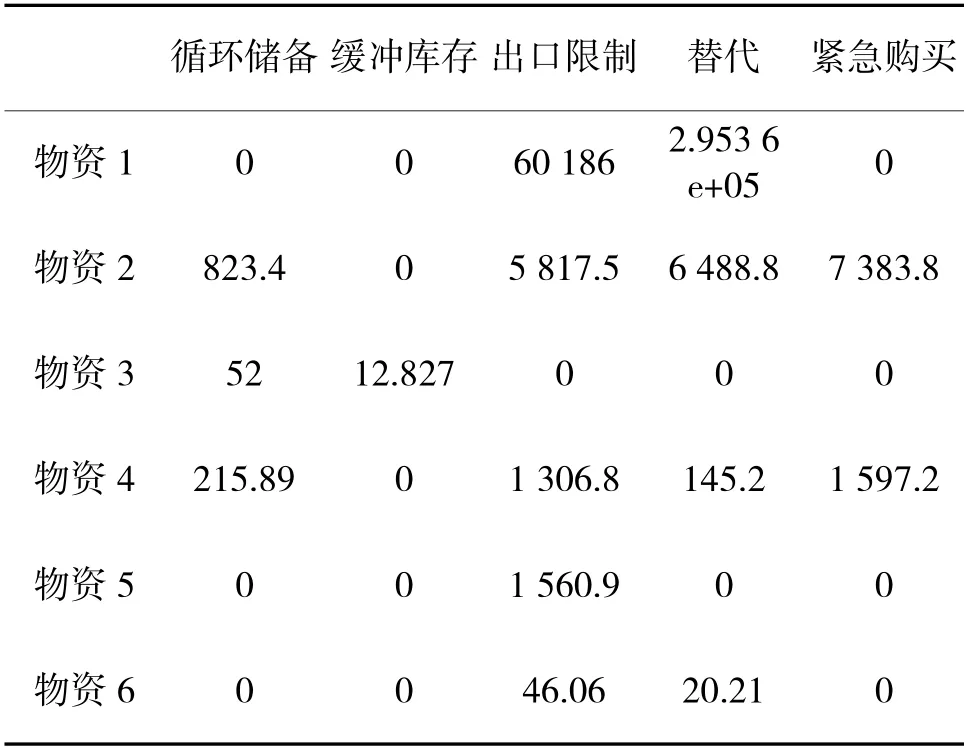
表6 优化方案（k=0.5，CUB=1 000 万）Table 6 Optimal solution（k=0.5，CUB=107）

表7 方案费用和效果（k=0.5，CUB=1 000 万）Table 7 Cost and effect of solution（k=0.5，CUB=107）

表8 和表9 是当k=1～0.5、平均总费用的上限CUB=2 000 万时的优化方案、费用、效果，最小平均总风险为0.020 423，平均总费用达到极限2 000 万。

表8 优化方案（k=1，CUB=2 000 万）Table 8 Optimal solution（k=1，CUB=2×107）

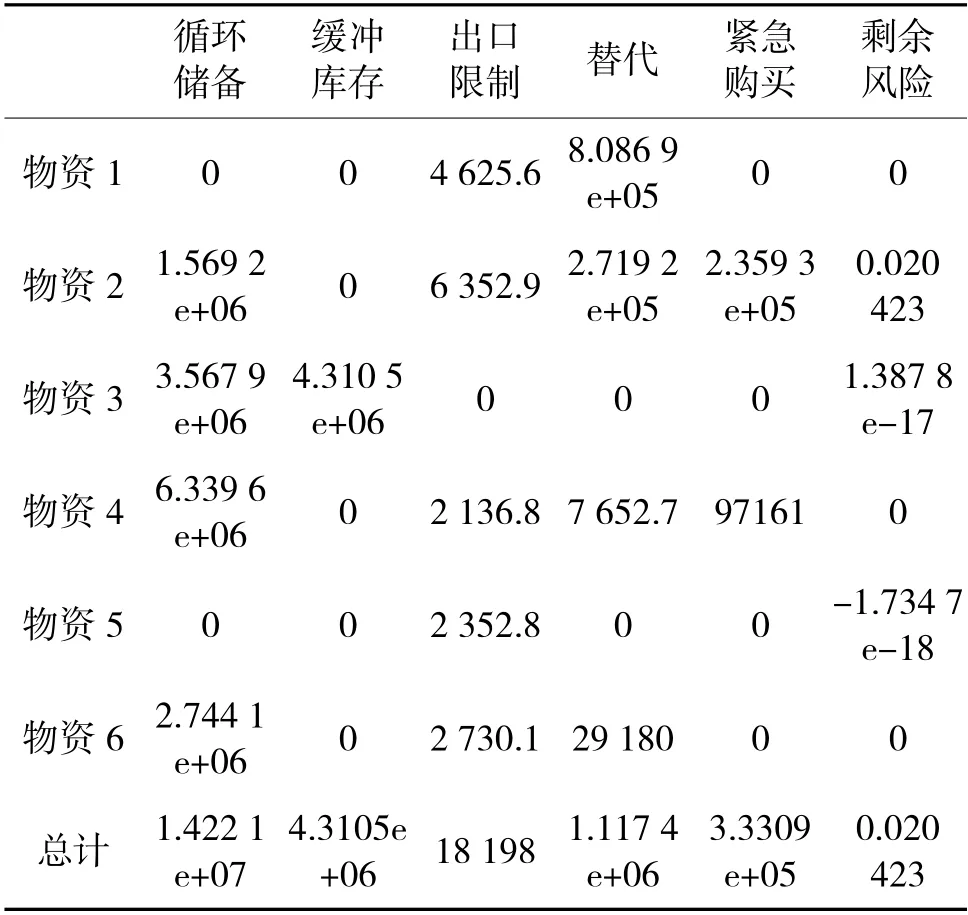
表9 方案费用和效果（k=1，CUB=2 000 万）Table 9 Cost and effect of solution（k=1，CUB=2×107）

表10 和表11 是当k=0.4、平均总费用的上限CUB=2 000万时的优化方案、费用、效果，最小平均总风险为0.034 614，平均总费用达到极限2 000万。

表10 优化方案（k=0.4，CUB=2 000 万）Table 10 Optimal solution（k=0.4，CUB=2×107）

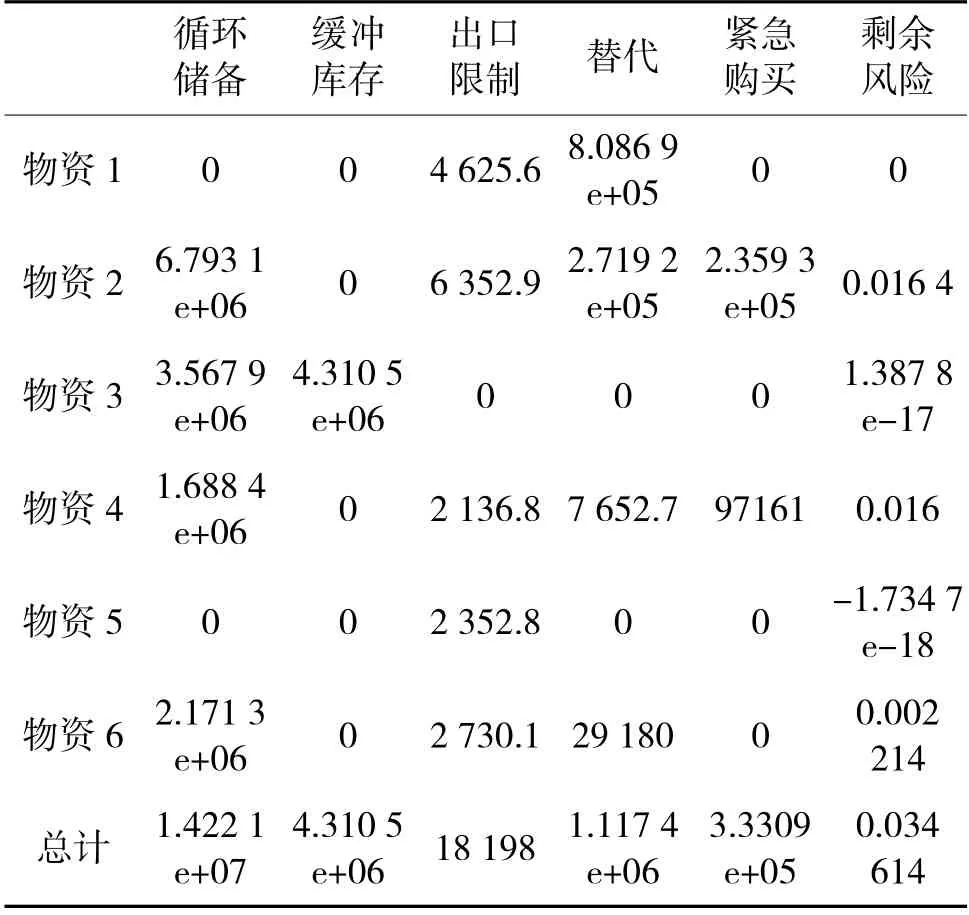
表11 方案费用和效果（k=0.4，CUB=2 000 万）Table 11 Cost and effect of solution（k=0.4，CUB=2×107）

表10 和表11 是当k=0.35、平均总费用的上限k=2 000万时的优化方案、费用、效果，最小平均总风险为0.043 237，平均总费用达到极限2 000 万。当k＜0.35，则无法得到最优解。

表12 优化方案（k=0.35，CUB=2 000 万）Table 12 Optimal solution（k=0.35，CUB=2×107）

通过比较表4～表13，随着预算费用增加，平均总风险随之降低；反之减少预算费用，平均总风险随之增加。随着每种战略物资的风险上限降低，平均总风险随之增加；反之每种战略物资的风险上限提高，平均总风险随之降低。可以这样理解，随着预算费用增加，风险上限提高，可行解范围扩大，更可能减少平均总风险，反之则会增加平均总风险。

表13 方案费用和效果（k=0.35，CUB=2 000 万）Table 13 Cost and effect of solution（k=0.35，CUB=2×107）

4.2.2 战争概率

当将战争概率调高PW=0.037，（k=0.6，CUB=1 千万）优化方案、费用、效果如表14～表15。与表4～表5 进行比较，战争概率调高之后，用于紧急购买的费用增加。这也就是说，当得知战争发生概率较大时，应更多选择紧急购买这种方式。

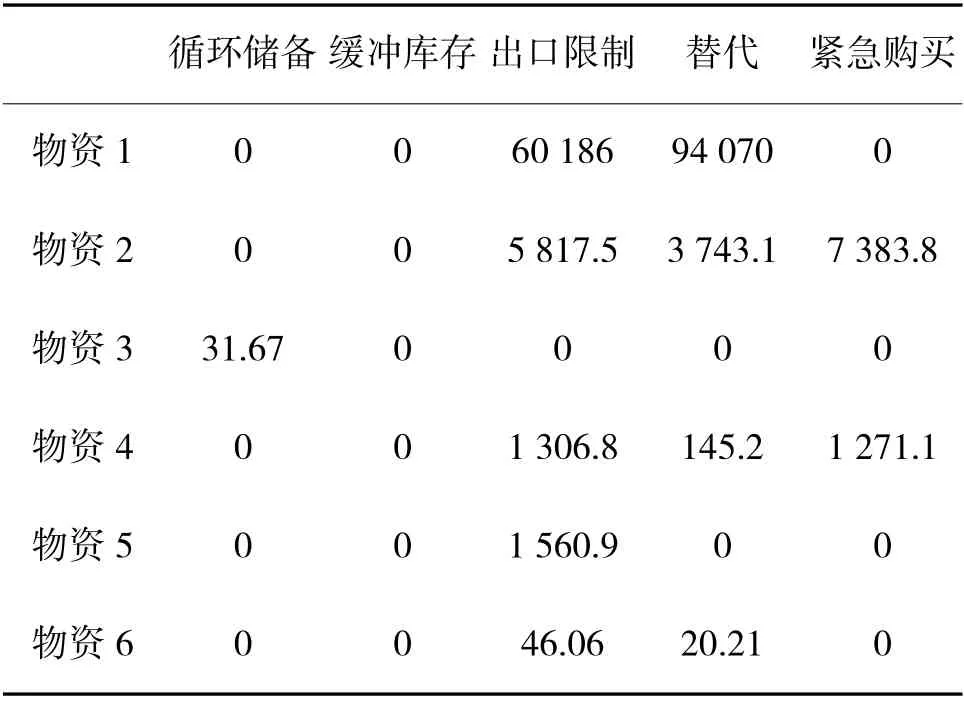
表14 优化方案（k=0.6，CUB=1 千万，PW=0.037）Table 14 Optimal solution（k=0.6，CUB=107，PW=0.037）

表15 方案费用和效果（k=0.6，CUB=1 000 万，PW=0.037）Table 15 Cost and effect of solution（k=0.6，CUB=107，PW=0.037）

4.2.3 缓冲库存租金率

缓冲库存租金率FBR=0.03，（k=0.6，CUB=1 000万）优化方案、费用、效果如表16～表17。与表4～表5 进行比较，缓冲库存租金率降低之后，用于缓冲库存的费用增加，缓冲库存成为比较有竞争力的补充方式。

表16 优化方案（k=0.6，CUB=1 000 万，FBR=0.03）Table 16 Optimal solution（k=0.5，CUB=107，FBR=0.03）

表17 方案费用和效果（k=0.6，CUB=1 000 万，FBR=0.03）Table 17 Cost and effect of solution（k=0.6，CUB=107，FBR=0.03）

5 结论

本文给出了一种基于风险的战略物资补充优化模型。描述了战略物资补充问题，分别介绍了补充方式、风险度量、补充费用计算。给出了模型假设，以及建立了非线性规划模型，提出了基于粒子群算法的模型求解算法。示例中给出了相关假设和数据，对平均总费用上限、风险上限、战争概率等因素进行了分析，验证了方法的可行性与有效性。该模型为管理战略物资储备提供了一种可行的方法，它基于战略物资风险，综合考虑许多规划参数（风险、费用、战争可能性、战略物资短缺严重程度、成功补充的可能性，以及决策者风险偏好），可以得到效费比较高的战略物资补充方案。