基于粗糙集的装甲兵分队作战能力评估*

程 燕，冯传茂，李为贵，刘家路，赵一唯

（陆军装甲兵学院蚌埠校区，安徽 蚌埠 233000）

0 引言

装甲兵分队是联合作战中地面突击作战的主要力量，采用科学有效的方法对其作战能力进行评估，能够为上级指挥员的决策部署提供可靠依据，对提高装甲兵分队整体作战效能有重要作用［1］。

在作战能力评估过程中，评估指标体系模型（基础）、评估方法（核心）和评估指标权重（关键）是3 个重要的方面，其直接影响评估结果的可信度和准确性［2］。目前，关于装甲兵分队作战能力评估问题的研究主要集中在评估方法和指标权重的确定，缺少对评估指标体系模型优化的研究。如：王钦钊等利用层次分析法（analytic hierarchy process，AHP）对装甲分队模拟训练成绩进行评估［3］，建立了成绩评估的数学模型，给出了指标权重计算方法，在实际的模拟训练成绩评估中取得理想效果；邵杰将AHP 法与改进的数据包络分析法有机结合［4］，建立装甲兵部队信息化作战能力的评估模型，给出权重计算方法，通过构建最优与最差的虚拟对象为标杆，以此对作战能力进行排序。叶志祥等构建了装甲分队作战能力评估体系［1］，对指标进行了重要性比较和筛选，利用AHP 法和熵权法确定指标权重，最后通过加权逼近于理想解的排序方法对评估结果进行排序。

上述方法存在以下问题：1）都是基于AHP 法确定指标权重，AHP 法依赖于专家经验、主观性强，会带来评估结果不准确的问题。2）缺少对评估指标体系模型优化的研究，仅文献［1］中通过专家咨询法来确定各指标的重要度，根据指标重要度进行比较和筛选，获得优化后的评估指标体系模型，但该方法同样受限于专家的专业领域、知识水平，优化结果带有较强的个人偏好。因此，评估指标体系模型优化的进一步研究是十分必要的。在实际应用中，为了使装甲兵分队作战能力评估指标更加全面，在构建评估指标体系时总是力图包含所有指标，这样会导致指标多、权重小、评估结果失真的问题［1，3］，也会导致评估模型维度较高、计算复杂等问题。由于各指标对评估结果的影响程度都是不同的，通常的做法是选取影响程度大的指标，剔除影响程度小的指标［1，5］。

根据以上分析，为了解决现有方法评估结果不准确、计算复杂的问题，本文提出基于粗糙集的装甲兵分队作战能力评估方法。粗糙集理论是一种能够有效处理不完整性和不确定性信息的数学工具［6-8］，其优势在于不要多组数据，从原始数据本身中就能挖掘潜在的信息；在保留关键信息的前提下消除重复、冗余的属性；根据数据本身的规律计算属性权重［9-11］。从作战要素的角度构建装甲兵分队作战能力评估指标体系，然后基于粗糙集属性重要度理论，给出评估指标约简和权重计算的方法，通过装甲兵分队真实演习数据进行评估分析，其结果与利用AHP 方法获得的结果进行相比，验证了本文方法的可靠性和有效性。

1 作战能力评估指标体系构建及指标的预处理

1.1 构建评估指标体系

在合成营的编成内，装甲兵作为合成营地面突击作战的主要力量，装甲兵分队的作战能力是指装甲兵在某个条件下完成作战任务的能力。由于面向作战任务具有较强的针对性，适用性较低，而面向作战要素具有简单明了、通用性较强的特点［2］。从装甲兵分队作战要素的角度进行分析，参考文献［1］中建立的装甲分队训练成绩评估指标体系，以及合成营新的作战能力构成，考虑主要从指挥决策、机动、火力打击、抗击突击和防护等5 个作战要素，构建装甲兵分队作战能力评估指标体系。在选择指标时，遵循系统性、关键性、可度量性和客观性的原则［3］。本文构建的评估指标体系层次图，如图1所示。

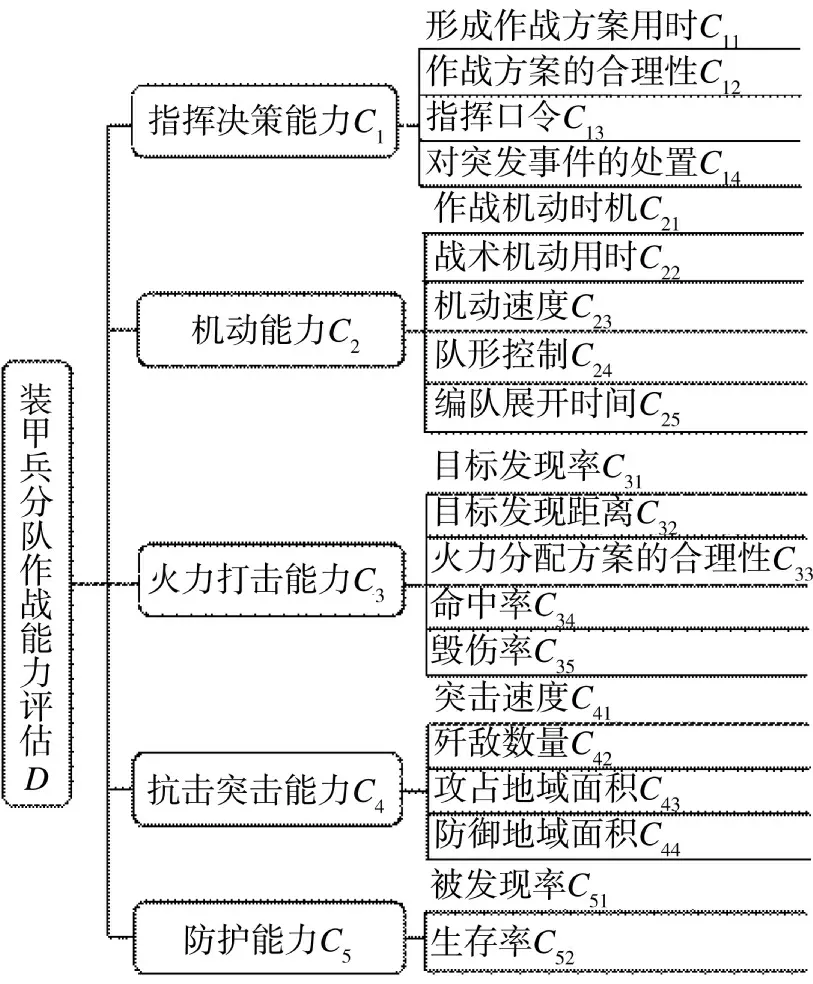
图1 装甲兵分队作战能力评估指标体系层次图Fig.1 Hierarchical figure of operational capability assessment indication system

1.2 评估数据的无量纲处理

从上述构建的评估模型可以看出，指标体系中既有定量指标也有定性指标，各指标的意义不同，需要进行无量纲处理。按百分制对各指标进行量化处理时，可分为4 类：

1）对于容易测量，取值越小越好的指标，此类指标有：C11、C51。

2）对于容易测量，取值越大越好的指标，此类指标有：C31、C32、C34、C35、C42、C43、C44、C52。

3）对于容易测量，取值适中的指标，此类指标有：C21、C22、C23、C25、C41。

4）对于不易测量的指标，采用多组专家打分综合评判的方式赋值，设置“优秀，良好，中等，一般，较差”5 个等级，按照百分制表示为［90，100］，［80，90），［70，80），［60，70），［0，60）。此类指标有：C1、C2、C3、C4、C5、C12、C13、C14、C24、C33。

对于上述第1）、2）和3）类指标，参考文献［3］中的处理方法，由于篇幅有限，不具体列出。

2 基于粗糙集的作战能力评估方法

2.1 评估指标体系约简方法

2.1.1 粗糙集理论［5，13］

定义1 决策表系统定义为S= {U，R，V，f }，其中，U 是非空有限对象集，称为论域；R={C∪D}，C∩D=Ø，C 和D 分别称为条件和决策属性集；对于r∈R，V=∪Vr是属性值的集合，Vr是属性r 的值域；f：U×R→V 是信息函数，其功能是给每个对象x∈U 的每个属性r∈R 赋值，即：f（x，r）∈Vr。

每一个属性子集P⊆R 决定一个等价关系ind（P），即：

等价关系ind（P）构成U 上的一个划分，用U/ind（P）表示，简记为U/P。

定义2 正域的定义。给定决策表系统S=（U，R，V，f），R={C∪D}，C∩D=Ø，属性ci∈C（i=1，2，...，m），U/ci表示ci对U 的划分，则D 的ci正域Posci（D）定义为：

在决策表中，为了获得属性的重要性，可以通过删除表中的某属性，看删除该属性后关系划分发生的变化，若发生的变化较大，则说明该属性的重要性高；反之，若发生的变化较小，则说明该属性的重要性低。

定义3 属性重要度的定义。给定决策系统S=（U，R，V，f），R={C∪D}，C∩D=Ø，属性ci∈C，D 的ci正域为PosP（D），ci和D 之间的依赖度定义为γci（D），ci关于D 的重要度定义为σ（ci），即：

根据定义可以看出，若|σ（ci）|＞0，说明删除属性ci后，关系划分发生了变化，则该属性是必要的；若|σ（ci）|=0，则说明删除属性ci后，关系划分没有变化；则该属性是不必要的；

定义4 属性权重的定义。给定决策系统S=（U，R，V，f），R={C∪D}，C∩D=Ø，C 和D 分别称为条件和决策属性集，ci∈C（i=1，2，...，m），则属性ci的权重为：

2.1.2 装甲兵分队作战能力评估指标约简方法

对于装甲兵分队作战能力评估，其决策表系统S={U，R，V，f }，其中，R=C∪D，C∩D=Ø，C 和D 分别称为条件属性集和决策属性集，即C 表示装甲兵分队作战能力评估指标的集合，ci∈C（i=1，2，...，m）表示其评估指标体系中某一个指标，D 表示装甲兵分队作战能力。

根据上述粗糙集属性重要度理论，对于装甲兵分队作战能力评估决策表系统，评估指标体系约简方法，步骤如下：

Step1：由式（1）计算ind（C）和ind（D）；

Step2：对于集合C=ci（i=1，2，...，m），依次删除ci后，同理计算ind（C-ci）；

Step3：由式（2）依次计算PosC（D）和PosC-ci（D）；

Step4：由式（3）和式（4）计算各指标的重要度σ（ci），若|σ（ci）|＞0，则ci为必要的指标，保留在装甲兵分队作战能力评估指标体系中；否则ci为不必要的指标，则从装甲兵分队作战能力评估指标体系中约简；

Step5：约简后的装甲兵分队作战能力评估指标体系为red（C）：

2.2 确定指标权重

根据上述指标重要度的计算结果和式（5）计算各指标的权重。指标的重要度越高，其权重就会越大。

2.3 作战能力评估

根据上述获取的各指标权重，利用线性加权法计算各次装甲兵分队作战能力［14］，即：

其中，wi为某指标的权重；yi为指标的值。

3 实例分析

本文以某重型合成营所属的装甲兵分队在训练基地进行对抗演习为背景，选择12 组代表性的实际收集的数据（考核评估数据、导调人员记录数据、专家打分数据等）为例，对其作战能力进行评估的具体处理步骤如下页图2 所示。

图2 作战能力评估步骤Fig.2 Operational capability assessment steps

3.1 初始数据无量纲处理和离散化处理

根据1.2 节内容，原始数据无量纲转换处理后，得到如表1 和表2 所示的无量纲数值。为了更好地对结果进行分析，对表1 和表2 进行离散化（数据取值范围为{1，2，3，4，5}）处理后，得到粗糙集知识表达系统［15］，如下页表3 和表4 所示。

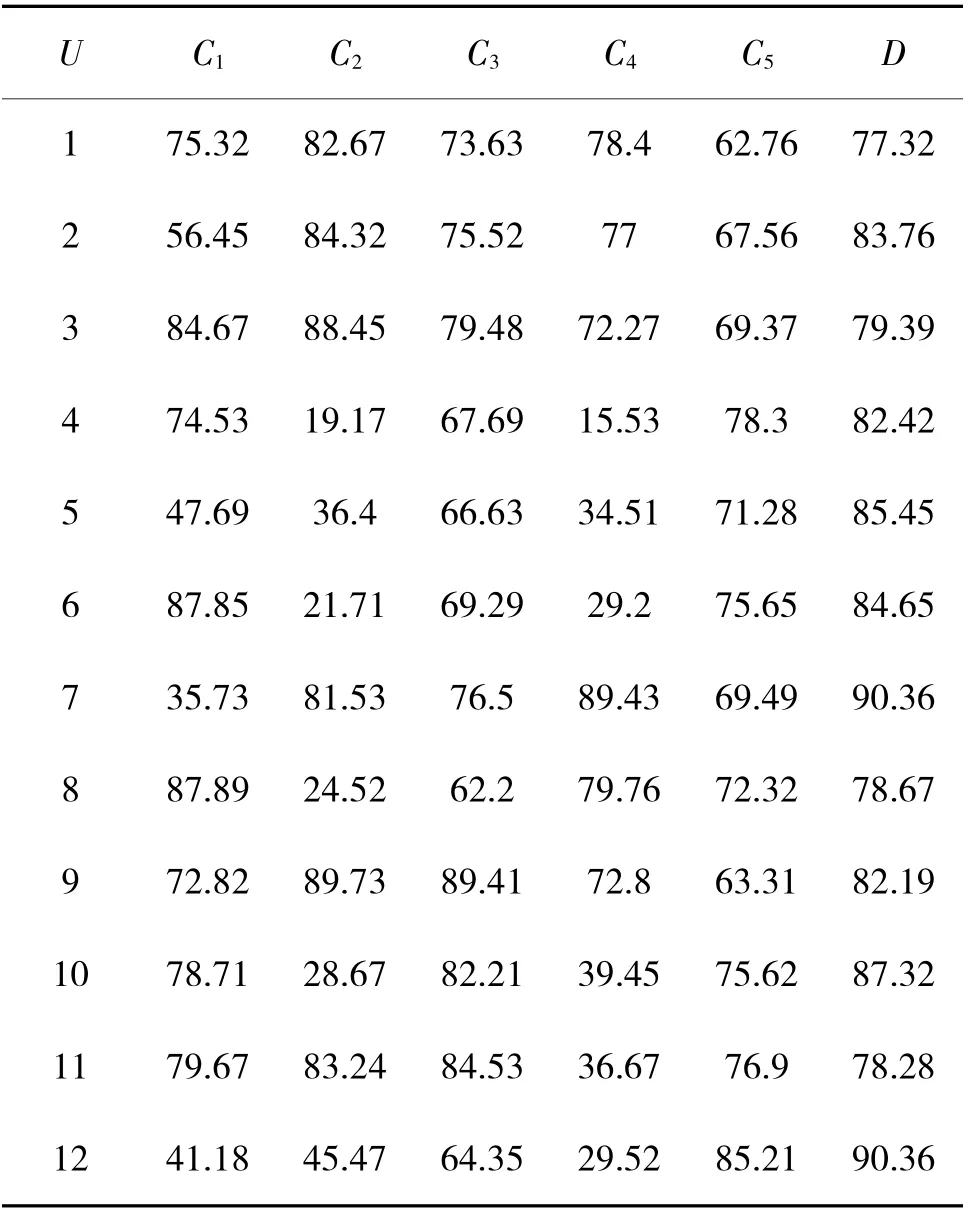
表1 一级指标无量纲数值Table 1 Dimensionless numbers of first-level indicators

表2 二级指标无量纲数值Table 2 Dimensionless numbers of second-level indicators

3.2 一级指标约简

根据表3 数据和2.1.2 节约简方法，可得：

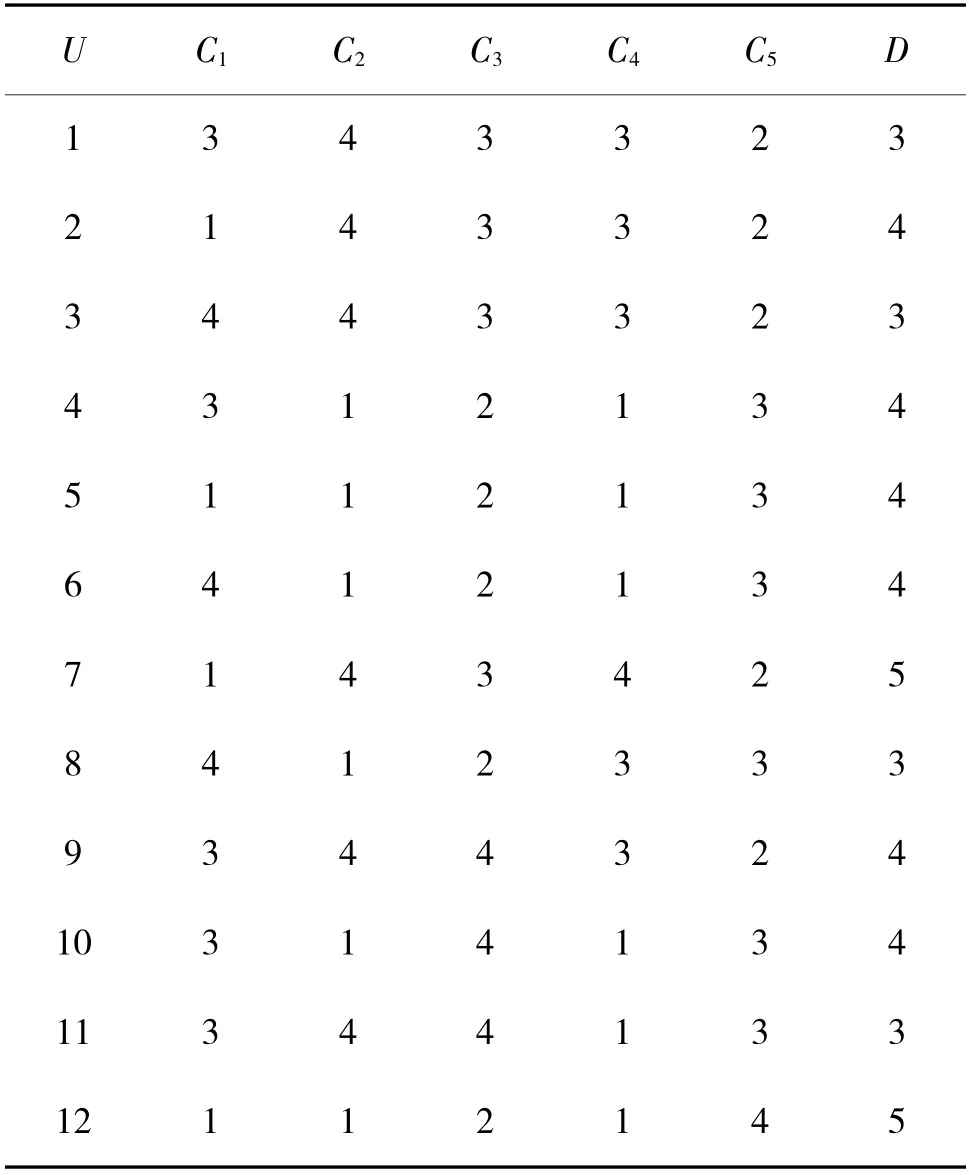
表3 一级指标离散化数值Table 3 Discretized values of first-level indicators

σ（C1）=γC（D）-γC-C1（D）=6/12，

σ（C2）=γC（D）-γC-C2（D）=2/12，

σ（C3）=γC（D）-γC-C3（D）=4/12，

σ（C4）=γC（D）-γC-C4（D）=4/12，

σ（C5）=γC（D）-γC-C5（D）=2/12；

因为σ（C1）＞0，σ（C2）＞0，σ（C3）＞0，σ（C4）＞0，σ（C5）＞0，所以5 个一级指标都是不可约简的，即Red（C）={C1，C2，C3，C4，C5}。

3.3 二级指标约简

根据表4 数据和上述2.1.2 节约简方法，同理可得：

表4 二级指标离散化数值Table 4 Discretized values of second-level indicators

1）在一级指标指挥决策能力C1下属的二级指标中，σ（C11）=3/12，σ（C12）=6/12，σ（C13）=2/12，σ（C14）=4/12。因此，C11、C12、C13和C14是必要指标，不可约简，即Red（C1）={C11，C12，C13，C14}。

2）在一级指标机动能力C2下属的二级指标中，σ（C21）=2/12，σ（C22）=3/12，σ（C23）=2/12，σ（C24）=0，σ（C25）=0。因此，C21、C22、C23是必要指标，不可约简，C24、C25是不必要指标，可约简，即Red（C2）={C21，C22，C23}。

3）在一级指标火力打击能力C3下属的二级指标中，σ（C31）=2/12，σ（C32）=0，σ（C33）=0，σ（C34）=2/12，σ（C35）=4/12。因此，C31、C34、C35是必要指标，不可约简，C32、C33是不必要指标，可约简，即Red（C3）={C31，C34，C35}。

4）在一级指标抗击突击能力C4下属的二级指标中，σ（C41）=0，σ（C42）=0，σ（C43）=7/12，σ（C44）=6/12。因此，C43、C44是必要指标，不可约简，C41、C42是不必要指标，可约简，即Red（C4）={C43，C44}。

5）在一级指标防护能力C5下属的二级指标中，σ（C51）=10/12，σ（C52）=11/12。因此，C51、C52是必要指标，不可约简，即Red（C5）={C51，C52}。

3.4 约简后的作战能力评估指标体系

根据上述一级和二级评估指标约简后的结果，可得出约简后的装甲兵分队作战能力评估指标体系，如图2 所示。

3.5 确定指标权重

根据上述各指标属性重要度的计算结果，由式（5）可得：

1）确定一级指标权重

一级指标C1、C2、C3、C4和C5相对于作战运用效能D 的权重为：

WD={C1，C2，C3，C4，C5}={0.333 3，0.111 1，0.222 2，0.222 2，0.111 1}。

图3 约简后的装甲兵分队作战能力评估指标体系Fig.3 The research assessment indication system about operational capability

2）确定二级指标权重

C1下属的4 个二级指标相对于C1的权重WC1={C11，C12，C13，C14}={0.2，0.4，0.133 3，0.266 7}；

C2下属的5 个二级指标相对于C2的权重WC2={C21，C22，C23，C24，C25}={0.2857，0.4286，0.2857，0，0}；

C3下属的5 个二级指标相对于C3的权重WC3={C31，C32，C33，C34，C35}={0.25，0，0，0.25，0.5}；

C4下属的4 个二级指标相对于C4的权重为WC4={C41，C42，C43，C44}={0，0，0.538 4，0.461 6}；

C5下属的2 个二级指标相对于C5的权重为：WC5={C51，C52}={0.476 2，0.523 8}。

根据上述计算结果，可得出指标体系中各二级指标相对于装甲分队模拟训练成绩D 的权重WD={C11，C12，C13，C14，C21，C22，C23，C24，C25，C31，C32，C33，C34，C35，C41，C42，C43，C44，C51，C52}={0.066 7，0.133 3，0.044 4，0.088 9，0.031 7，0.047 6，0.03 17，0，0，0.055 6，0，0，0.055 6，0.111 1，0，0，0.119 6，0.102 7，0.052 9，0.058 2}。

3）作战能力评估及结果分析

利用上述实例获取的装甲兵分队作战能力评估指标体系的权重，对装甲兵分队作战能力进行评估。选择3 组装甲兵分队对抗演习收集的数据，经过无量纲处理后，如表5 所示。

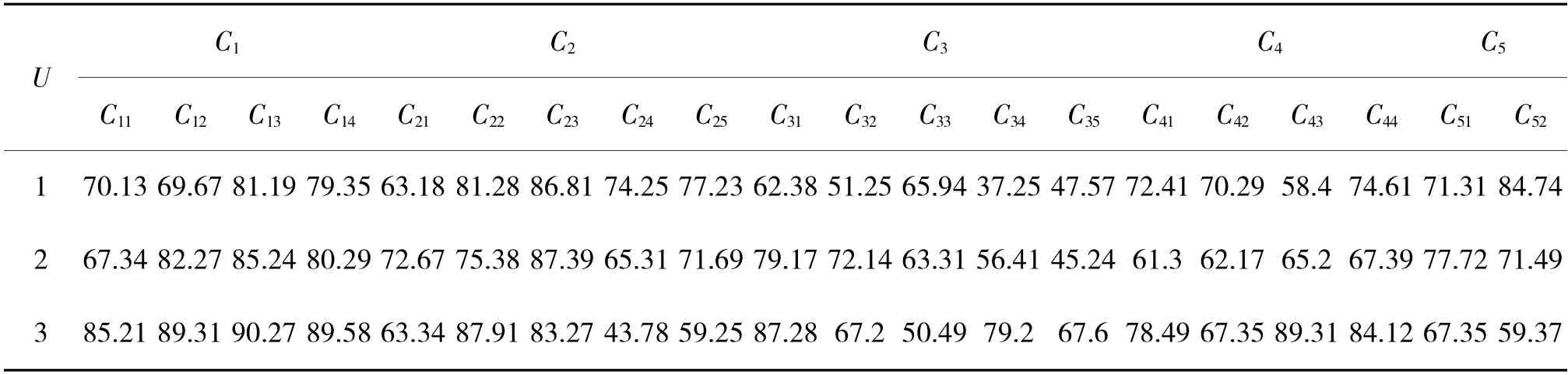
表5 装甲兵分队各评估指标评价结果无量纲数值Table 5 Dimensionless numbers of each assessmentindicator result of detachment of armored forces

为了验证本文提出的基于粗糙集理论的装甲兵分队作战能力评估方法的有效性和可靠性，通过与AHP 法［3］获得的评估结果进行比较。

利用AHP 法（本文省略AHP 方法计算过程）得到 的 各 指 标 权 重W'D={C11，C12，C13，C14，C21，C22，C23，C24，C25，C31，C32，C33，C34，C35，C41，C42，C43，C44，C51，C52}={0.056 8，0.165 5，0.033 8，0.098 4，0.0302，0.047 8，0.018 3，0.007 5，0.010 5，0.040 8，0.015 7，0.024 8，0.067 1，0.106 3，0.013 3，0.015 5，0.084 6，0.068 9，0.031 3，0.062 9}。

则利用本文方法获得的指标权重得到的各装甲兵分队的作战能力分数为：D1=67.42，D2=70.6，D3=81.5。

则利用层次分析法获得的指标权重得到的各装甲兵分队的作战能力分数为：D'1=67.05，D'2=70.26，D'3=79.73。

结果分析：

1）将本文方法与AHP 法获得的指标权重进行对比，如下页图4 所示，其中，RS 表示本文方法。从图中可以看出，指标C12权重都是最大的，本文RS方法约简的指标C24、C25、C32、C33，C41和C42在AHP方法中也是“次要”指标，权重值小于或远远小于0.02，对作战能力的评估影响较小。因此，两种方法获得的指标权重分布基本相近。而RS 法是根据装甲兵分队真实数据获取指标权重，不完全依赖于专家偏好，减少了人为的主观因素的干扰，使结果更具真实性。同时，RS 法对评估指标体系进行约简，简化了指标体系，降低了评估模型维度，提高了计算速度。

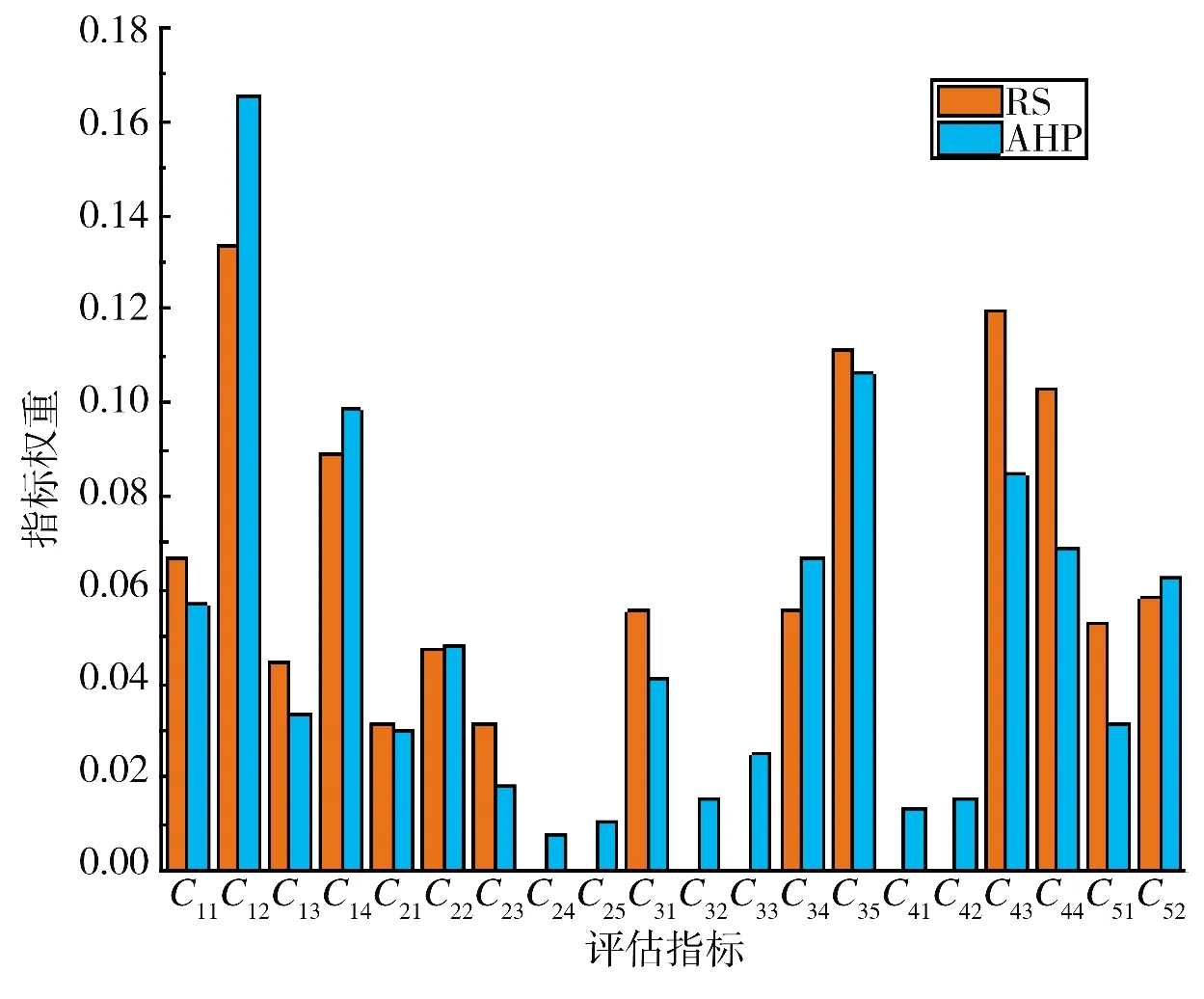
图4 评估指标权重对比图Fig.4 Weight comparison chart of assessment indicators

2）比较两种方法所获得的装甲兵分队作战能力评估结果，均为：D3＞D2＞D1（D'3＞D'2＞D'1），都是第3组装甲兵分队作战能力最强。

通过以上分析，验证了本文提出的基于粗糙集属性重要度理论的装甲兵分队作战能力评估方法的可靠性和有效性。

4 结论

本文针对装甲兵分队作战能力评估结果不准确、计算复杂的问题，提出了基于粗糙集理论的计算方法。首先，构建了基于作战要素的装甲兵分队作战能力评估指标体系，然后，基于粗糙集属性重要度理论给出了评估指标体系进行约简和权重确定的方法，克服了因评估指标多和依赖专家经验知识带来的评估结果不准确、计算复杂问题的不足，为装甲兵分队作战能力评估提供了更加合理的指标体系和指标权重。通过装甲兵分队真实演习数据进行评估分析，与AHP 方法获得的结果进行对比，本文方法有更好的评估结果和评估性能，验证了该方法的有效性和可靠性，为装甲兵分队作战能力评估提供了一种新的思路，为上级指挥员决策部署提供了可靠的依据。