超声速无尾飞行器最小阻力增量控制分配方法*

苏茂宇，胡剑波，王应洋，贺子厚，丛继平，韩霖骁

（空军工程大学装备管理与无人机工程学院，西安 710051）

0 引言

近年来，穿透性制空作战飞机在如何发展下一代战斗机的讨论中被广泛提及，其全向隐身性、超机动性、远航久航等系列能力将会推动未来空战形态发生革命性变化［1］。而超声速无尾飞行器（supersonic tailless aerial vehicle，STAV）在低可探测性、超声速性能等方面均具有优异表现［2-3］，是进行穿透性制空作战的绝佳选择。

垂直尾翼的取消使STAV 的雷达反射面积（radar cross section，RCS）减小、隐身性能增强，但也导致STAV 的水平控制效率及横向稳定性有所下降。为此设计者开发了新型的操纵面系统，将常规舵面与嵌入面、全动翼尖等新型操纵面相结合，以保证足够的操纵效率，同时系统的冗余性使飞行器有多种操纵面偏转方案满足控制需求［4］。不同偏转方案下的飞行阻力存在较大差异［5］，寻求一种使飞行阻力维持在较低水平的偏转组合，即求解最小阻力控制分配问题，可以减少STAV 在飞行过程中，尤其是超声速巡航阶段的燃料消耗，对其增大航程、发挥超声速性能优势具有重要意义。

然而，解决STAV 的最小阻力控制分配问题面临以下困难：一是STAV 操纵面系统控制效率非线性强、交叉耦合作用严重，线性控制分配方法无法实现控制指令的有效分配；二是舵面偏转与飞行阻力间的关系复杂，多以气动数据的形式呈现，难以用显式表达式进行准确描述，进而无法将阻力写为数学规划类方法可以求解的性能指标。

针对控制效率非线性问题，文献［6］选取三阶多项式函数对非线性舵效模型进行拟合，并使用序列二次规划算法进行求解，但该方法的精度受限于拟合多项式函数的阶数，阶数过低时无法达到精度要求，阶数过高又会导致计算负担超出能力范围；遗传算法［7］、强化学习［8］等智能方法也被用于处理该问题，此类方法虽然结果较为理想，但运算速度偏慢；针对舵面间交叉耦合作用，文献［9］将其视为一种不确定性，基于混合优化的原理提出了一种鲁棒控制分配方法，但该方法在克服耦合作用的同时牺牲了耦合舵面的部分控制潜力，使舵面利用率降低；文献［10］提出一种基于补偿的线性规划方法处理飞翼布局飞机的交叉耦合作用，但通用性不强。

针对最小阻力控制分配问题，文献［11］采用直接分配法进行了最早研究，将阻力作为一个新的维度添加到力矩可达集（attainable moment subset，AMS）构成目标可达集（attainable objective subset，AOS），但由于非线性舵效的AMS 求取十分困难，这种方法应用局限性较大；针对飞行阻力与舵面偏转关系复杂的问题，文献［12］将最小阻力模态用最小舵偏模态进行近似，但对STAV 这种不同操纵面控制效率差异较大的系统，所得舵面偏转组合产生的阻力仍有较大缩减空间；文献［13］采用文献［6］的基本思想，通过三阶多项式对阻力系数曲线进行拟合，而后作为性能指标通过数学规划类方法进行优化。

本文基于增量非线性控制分配［14］（incremental nonlinear control allocation，INCA）方法，将STAV 非线性舵效模型改写为增量形式，使线性控制分配（linear control allocation，LCA）方法可用于非线性控制分配（nonlinear control allocation，NCA）问题的求解。在此基础上，给出一种同时考虑分配精度与飞行阻力的增量形式混合优化性能指标，并利用有效集二次规划算法解算最小阻力操纵面偏转组合。最后，在MATLAB/Simulink 仿真环境下，对本文提出的STAV最小阻力控制分配方案的有效性进行综合验证。

1 STAV 的控制分配问题

STAV 进行穿透性制空作战需具备良好的跨声速与超机动性能，但现有的飞翼布局飞行器多将进气道设置在机体上方，限制了大迎角和航向机动性。美国Lockheed Martin 公司设计的先进控制面（innovative control effectors，ICE）飞行器模型在隐身性、机动性与超声速性能方面性能优异，是一种极具潜力的STAV 构型［15］，其结构如图1 所示。

图1 ICE 飞行器结构示意图Fig.1 Sketch map of structure of ICE flight vehicle

ICE 飞行器配置有多轴推力矢量及11 个气动操纵面，详细特性如表1 及式（1）所示。

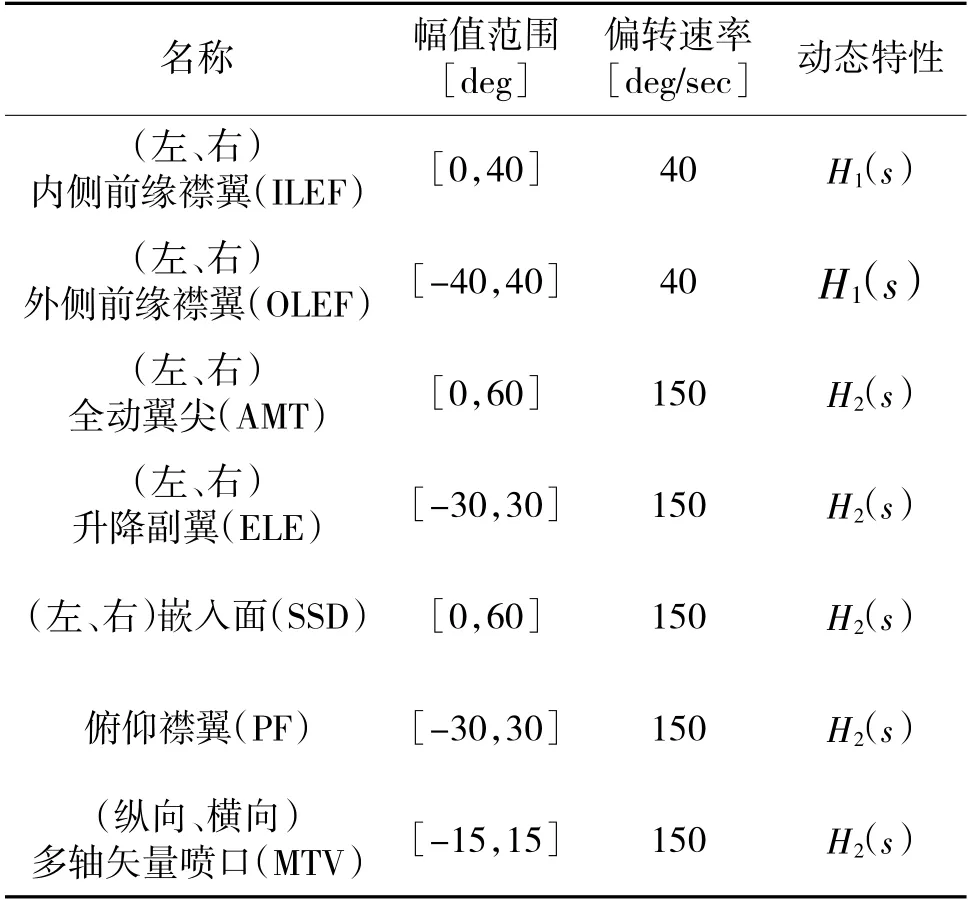
表1 ICE 飞行器操纵面特性Table 1 Control surface feature of ICE flight vehicle

为协调冗余操纵面进行合理偏转，ICE 飞行器的飞行控制系统采用图2 所示的模块化设计，即将飞行控制律和控制分配律分为两个模块单独进行设计［16］。飞行控制律解算出飞行器姿态、位置变化所需的虚拟控制指令c，而后利用控制分配律对各操纵面的偏转量δ 进行求解，以产生与虚拟控制指令相等或偏差足够小的虚拟控制量。控制分配的一般数学描述及简化形式如式（2）所示。

图2 多操纵面飞行器的典型控制结构图Fig.2 Typical control structure of multi control surface flight vehicle

然而，如图3 和图4 所示：在Ma=1.2、H=4 572 m的条件下，左全动翼尖的偏转与俯仰力矩系数之间呈现非单调非线性特点，且这种关系在不同迎角下差异巨大，若使用基于多项式拟合的数学规划求解方法，每当迎角α 等飞行条件发生改变时都要重新拟合，步骤复杂且实时性差；嵌入面的偏转对位于其气流下游的升降副翼影响巨大，当嵌入面偏转超过20°时，升降副翼产生俯仰力矩的效率几乎降为零，基于补偿的线性规划方法难以处理这种强耦合作用；在其他操纵面保持配平角度不变的情况下，左全动翼尖偏转角度与阻力系数间的关系无法用线性表达式描述，多项式拟合也会存在较大误差；图4（b）体现出舵面间的耦合作用对阻力产生效率有巨大影响，这使得ICE 飞行器的阻力特性更加难以刻画。通过上述典型现象可以看出，处理最小阻力非线性控制分配问题的传统方法对STAV 这一对象难以适用，需要一套从舵效非线性处理到性能指标构建，再到舵偏量求解的控制分配新方法。

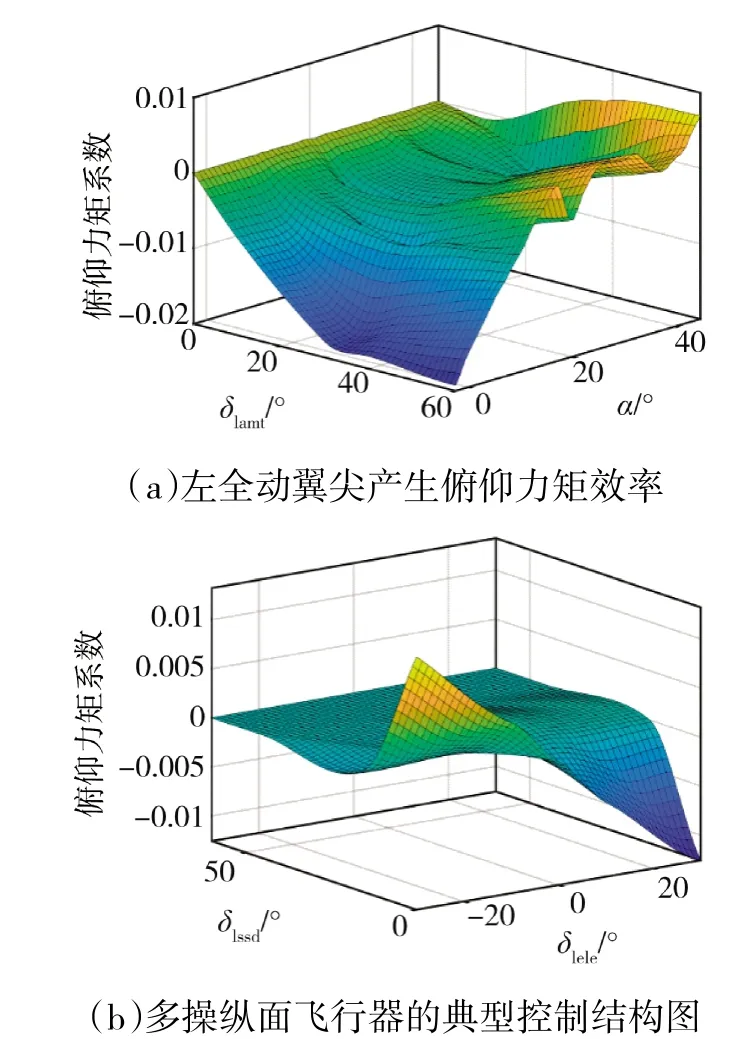
图3 ICE 飞行器部分操纵面控制效率图Fig.3 Control efficiency figure of partial control surface of ice flight vehicle

图4 ICE 飞行器部分操纵面阻力效率曲线Fig.4 Drag efficiency curve of partial control surface of ice flight vehicle

2 最小阻力增量控制分配

针对现有方法无法满足STAV 最小阻力控制分配要求的问题，本文在充分考虑分配误差、实时性、实现难易程度的基础上，使用INCA 方法，按照舵效模型增量形式重构、混合优化性能指标构建、数学规划求解的思路进行设计。

2.1 INCA 方法

INCA 方法基于分段线性化思想和时间尺度分离原则，将非线性舵效模型改写为增量形式，并将舵效模型雅可比矩阵作为局部控制效率矩阵，根据操纵面位置反馈不断更新，利用再分配广义逆、数学规划等传统方法求解每一运算周期内的舵偏增量。首先，对舵效模型表达式在点处进行一阶泰勒展开：

式中，x0、δ0、分别为上一运算周期结束时的飞行状态、操纵面偏转角及虚拟控制量。

由于飞控计算机的采样频率通常在100 Hz 左右，采样间隔足够小，根据时标分离原则，飞行状态x 相对于操纵面偏转量δ 为慢变量，在一个步长内可将状态x 视为常值，式（4）可简化为雅可比矩阵乘以相邻两步操纵面偏转量差值的形式：

由此即完成了控制分配问题在增量形式下的重构，将NCA 问题转化为LCA 方法可以解决的形式。INCA 方法流程如图5 所示。

图5 INCA 方法流程图Fig.5 INCA method flow

飞行控制律解算出虚拟控制指令c后，与操纵面上一步产生的虚拟控制量做差得到Δc，输入到INCA 模块中，以随着操纵面偏转量δ 实时更新的雅可比矩阵作为操纵面控制效率矩阵，利用再分配广义逆、二次规划等常用分配算法解算出舵偏变化量Δδ，并与前一步的总舵偏量δ0相加得到舵偏指令δc，最终使舵面偏转δ、产生虚拟控制量。

根据INCA 的构建过程可以看出其主要具有以下优势：

1）精度较高且实时性较好。INCA 充分考虑了飞控计算机的离散运行方式，通过实时计算雅可比矩阵得到局部控制效率矩阵，将NCA 问题转化为每个运算周期内的LCA 问题，使得运算量小的常规LCA 方法仍然适用。

2）消除了操纵面动态特性带来的分配误差。传统控制分配方法往往假设δc=δ，忽略了操纵面动态特性导致的分配误差，而INCA 通过操纵面实时位置δ0与虚拟控制量 的反馈，有效补偿了操纵面动态误差。

3）可以有效处理操纵面约束。幅值与速率限制被统一为式（8）所示的增量形式，降低了操纵面约束，尤其是速率约束给控制分配问题带来的困难。

2.2 最小阻力性能指标构建

飞行器阻力可分为两类，一类是与操纵面偏转无关的零升阻力、诱导阻力等，一类是由操纵面偏转产生的型阻与波阻［17］。其中，配平舵偏越小型阻越小，对阻力维持在较低水平越有利，因此，有控制分配研究将总舵偏量最小（minimum deflection，MD）近似为最小阻力性能指标，形式如式（9）：

为便于在INCA 框架下利用数学规划类方法进行求解，可将上式改写为混合优化形式：

然而，如图6 所示，由于STAV 各操纵面的阻力产生效率差异大，优先使阻力产生效率较高的操纵面维持在较小的偏转角度往往可以使飞行阻力更小，因此，可以对式（10）中权值矩阵W 各元素的大小进行设置，给产生阻力效率高的操纵面设置一较高的惩罚值，以尽量避免这类舵面的偏转。

图6 ICE 飞行器操纵面阻力效率曲线Fig.6 Drag efficiency curve of control surface of ICE flight vehicle

但这种基于权值设置（weights setting，WS）方法存在明显缺陷：操纵面偏转角度与其产生的阻力系数之间并非线性关系，固定的权值矩阵无法在各类条件下均保证阻力最小。为避免这一缺陷，仍可以采用INCA 的基本思想，将阻力系数的增量与分配误差相结合形成最小阻力混合优化指标，使每一次运算在满足分配精度要求的同时，阻力增量尽量小，并最终使飞行器阻力在整个过程中维持于较低水平。

将飞行器产生的阻力系数写为增量形式：

其中，阻力系数CD通过对飞行器在机体坐标系下，各轴上的力系数及飞行器推力系数CT进行坐标变换求得：

β 为飞行器侧滑角。

式（12）中的偏导数仍通过类似于式（7）的方式求得：

将虚拟控制指令跟踪误差最小与阻力最小两个目标结合，写为混合优化形式：

进一步考虑到基于阻力系数增量（drag coefficient increment，DCI）的性能指标为达到最小，会过度使用阻力产生效率较低且力矩产生效率较高的操纵面，导致其过早达到饱和。这会产生两个问题，一是饱和操纵面将无法再参与剩余力矩指令的分配，从而被迫使用阻力产生效率较高的操纵面，导致飞行器无法始终达到阻力最小；二是频繁达到幅值边界会使操纵面故障概率增加，不利于飞行器整体可靠性。上文提到，飞行器的配平偏角越小，阻力也越小，因此，可考虑将该方法与MD 性能指标相结合，达到既缓解舵面饱和又进一步降低阻力的目的。这种基于改进型阻力系数增量（modified drag coefficient increment，MDCI）的混合优化性能指标形式如式（17）所示：

式中，ε 为调节因子，取为一极小量，保证舵偏最小不会成为主要目标；W 仍取为单位阵。

注1：该性能指标的构建机理在于综合考虑飞行器操纵面总偏转量与阻力效率的非线性这两个因素对飞行阻力的综合影响，兼具MD、DCI 两种性能指标在减小飞行阻力方面的优势，在满足分配精度要求的前提下达到图7 所示的效果。

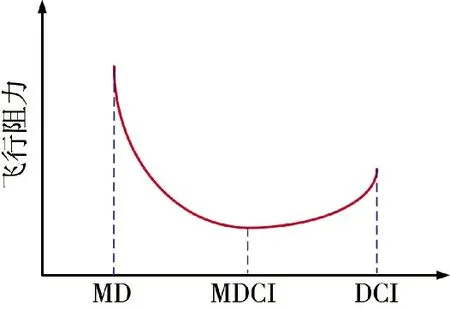
图7 MDCI 预期效果图Fig.7 Anticipated effect of MDCI

注2：在明确相关物理量数量级的前提下对矩阵Q 中各元素及调节因子ε 进行设置，这直接关系到分配精度、阻力大小及操纵面饱和程度。阻力与分配精度是一对矛盾，应首先给Q 设置的足够大，然后逐步向下调整，再适度增大ε，根据误差和阻力要求确定参数。

在完成增量形式下的控制分配问题重构及最小阻力混合优化性能指标构建的基础上，需要对操纵面实际偏转量进行最终求解。二次规划的有效集方法与线性规划问题中的单纯形法基本思想一致，均为迭代点沿约束边界前进，直至到达问题的最优点。该方法与在分配广义逆法、不动点法相比，运算时间在同一数量级上，但解的质量更好，故本文选择使用有效集二次规划算法执行这一步骤。

由此便完成了STAV 最小阻力控制分配问题的建模与求解，图8 对方法流程进行了总结：

图8 最小阻力INCA 方法流程Fig.8 Minimum drag INCA method flow

3 仿真与分析

为验证INCA 方法及本文提出的基于气动数据的抗饱和混合优化性能指标在处理STAV 最小阻力控制分配问题中的有效性，在Matlab/Simulink 环境中，以包含操纵面动态特性的ICE 飞行器模型为对象，在超声速巡航条件下给定力矩指令，使用INCA方法结合本文提到的MD、WS、DCI、MDCI 4 种性能指标进行对比分析。

3.1 仿真参数设置

在Ma=1.2、H=4 572 m（15 000 ft）、α=2°、β=0°的飞行条件下，参照文献［7］给定力矩指令为

操纵面动态特性与表1 一致，采样频率为100 Hz。文献［8］指出，飞行器在巡航阶段应尽量避免矢量操纵面的偏转以延长矢量装置使用寿命，且这不会影响任务执行效果，故本文使用ICE 飞行器的11个气动操纵面进行控制分配方案验证。4 种最小阻力INCA 方案参数设置如表2 所示。

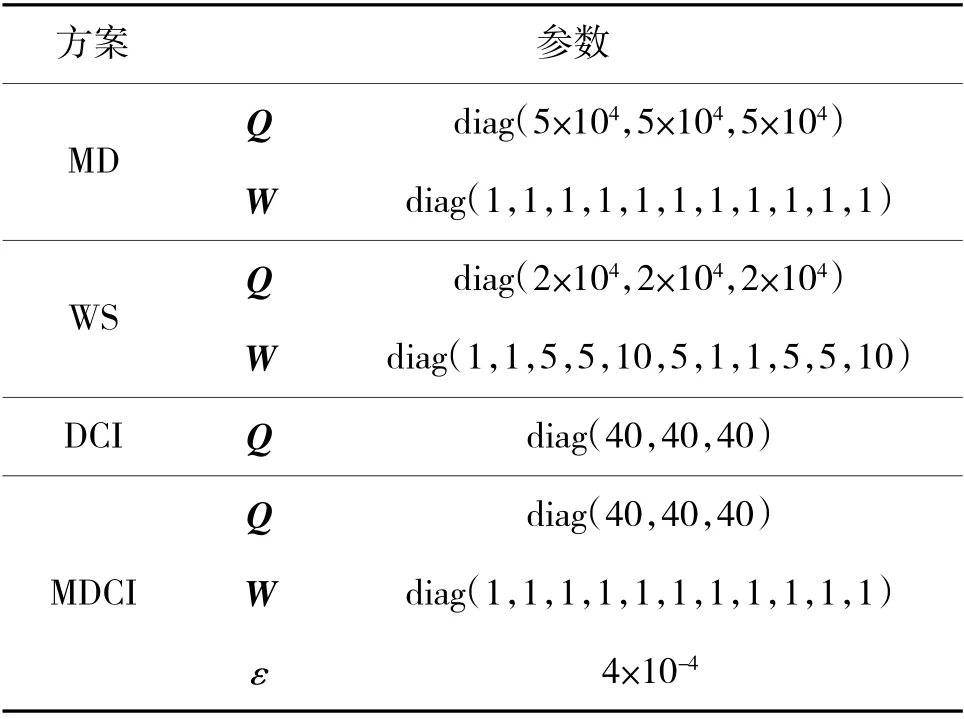
表2 性能指标参数设置Table 2 Performance index parameter setting

3.2 性能比较

将平均误差定义为式（19）所示的标准差形式：

n 为采样次数。4 种INCA 方案实际产生的力矩及平均分配误差分别如图9、下页表3 所示。可以看出，使用有效集二次规划进行求解的INCA 方法可以实现力矩指令的有效分配，其中，MD 方案误差最小，MDCI 方案误差最大，但在对控制分配精度要求较低的中高空条件下，这种差异往往可以忽略不计。

表3 4 种INCA 方案性能对比Table 3 Performance comparison of 4 kinds of INCA schemes

图9 力矩指令跟踪曲线Fig.9 Torque command tracking curve

进一步分析4 种INCA 方案对应的操纵面实际偏转曲线及平均偏转量结果如下页图10 和图11所。不同性能指标下操纵面偏转情况差异较大，MD方案相较于其他3 种方案更多使用阻力产生效率较高的嵌入面，故在图12 阻力曲线中，使用该方案产生的阻力相对最高；DCI 与MDCI 操纵面偏转大致接近，主要差别在于MDCI方案对俯仰襟翼的使用更少，饱和现象有所缓解，而图13 所示的调节因子与飞行阻力间的关系曲线与图7 变化趋势一致，当调节因子较小时，MDCI 方案与DCI 方案接近，当调节因子较大时，MDCI 方案与MD 方案接近，ε 取值在3.2×104左右时，MDCI 方案效果最佳，这证明了MD 方案与DCI 方案的适当结合，可以在牺牲一定分配精度的条件下实现飞行阻力的进一步降低。

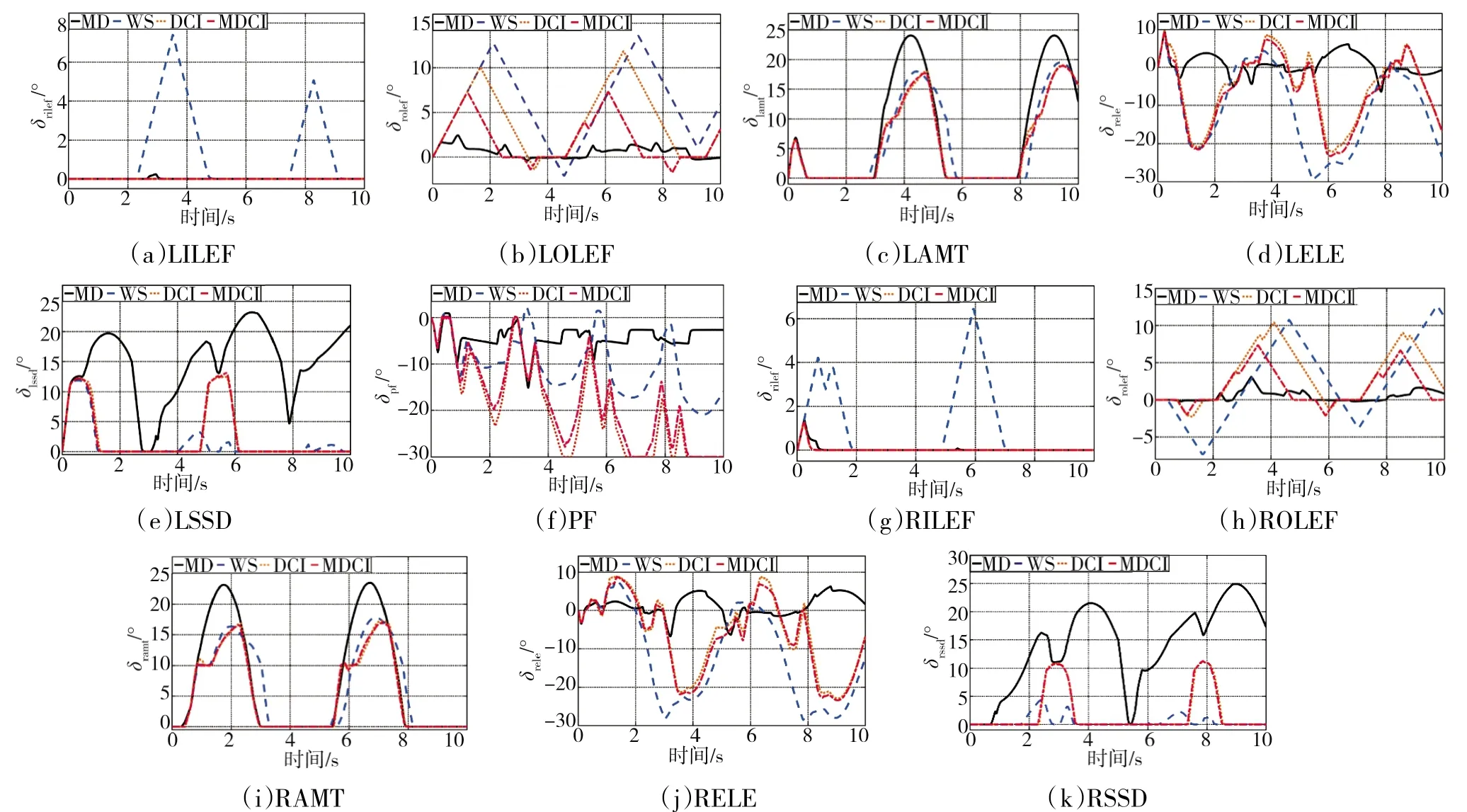
图10 操纵面偏转曲线Fig.10 Deflection curve of control surface

图11 操纵面平均偏转量Fig.11 Average amount of deflection of control surface

图12 4 种INCA 方案下飞行阻力变化曲线Fig.12 Flight drag variation curve of 4 kinds of INCA schemes

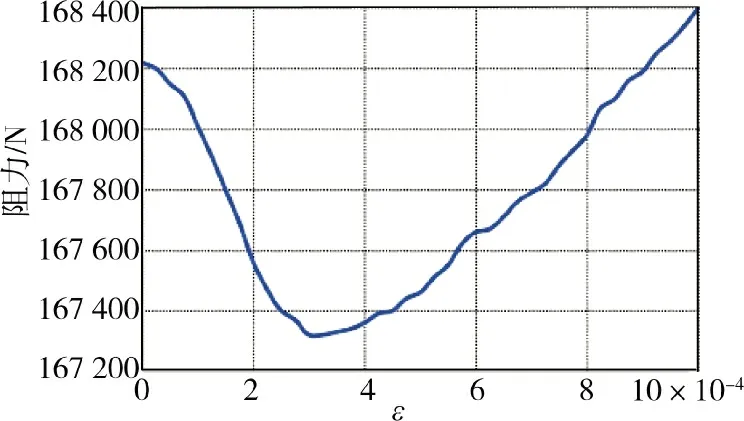
图13 阻力-调节因子变化曲线Fig.13 Drag-ε variation curve

4 结论

本文针对STAV 在超声速巡航条件下的最小阻力控制分配问题完成了以下工作：

1）采用INCA 方法对STAV 控制分配问题进行了重构，使传统的LCA 方法仍可以处理NCA 问题。

2）在INCA 框架下提出了一种基于阻力系数增量的混合优化性能指标，结合有效集二次规划算法，形成了一套完整的STAV 最小阻力控制分配问题解决方案。

3）以ICE 飞行器为模型，在超声速条件下对本文方法的指令分配精度及飞行阻力进行了仿真实验，通过对比分析验证了INCA 处理STAV 非线性控制分配问题的有效性。

本文提出的DCI、MDCI 方案可降低超声速巡航阶段20%以上的飞行阻力，对STAV 降低飞行阻力、减少燃料消耗具有积极意义，也可以此为基础进一步开展STAV 的多目标控制分配等研究。