数学之美:杨辉三角的奇特性质
2023-04-12 07:02:12万广磊摘编
初中生世界 2023年11期
万广磊 摘编
杨辉三角,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉1261 年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡在1654年发现这一规律,所以这个排列又叫作帕斯卡三角形。
就是这个看上去平平无奇的数字三角形,却有一些非常奇妙甚至是神秘的特性,本文将一一为同学们揭晓。
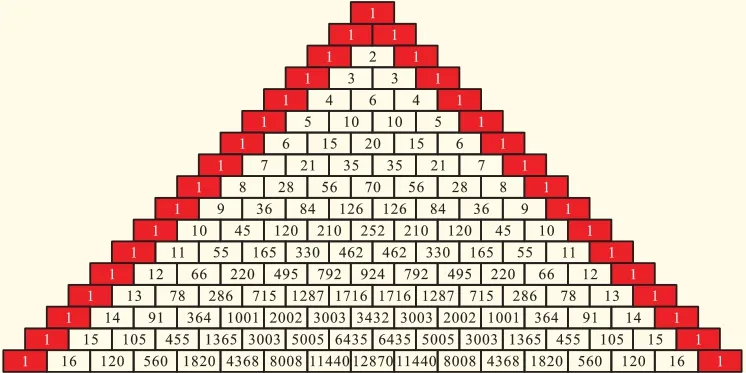
最外层的数字始终是1

第二层是自然数列

第三层是三角数列
什么是三角数列?看此图,这个数列中的数字始终可以组成一个完美的等边三角形。比如:3=1+2,此等边三角形可以分为2行,从上到下每一行分别是1 个点、2 个点;6=1+2+3,此等边三角形可以分为3行,从上到下每一行分别是1 个点、2 个点、3 个点;10=1+2+3+4,此等边三角形可以分为4 行,从上到下每一行分别是1 个点、2 个点、3 个点、4个点……
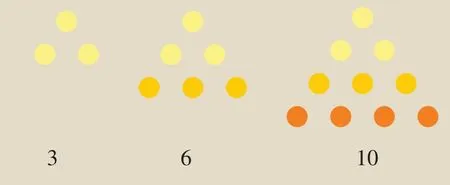

三角数列相邻数字相加可得方数数列
什么又是方数数列呢?与三角数列相似,它的数字始终可以组成一个正方形。

每一层的数字之和是一个呈2倍增长的数列,为2的n-1 次方。

斐波那契数列
没错,如果按照一定角度将直线上的数字相加,我们也可以从杨辉三角中找到隐藏的斐波那契数列。

分形结构
可以被特定数整除的数字,形成了奇妙的分形结构。

可以被2 整除的数字

可以被3 整除的数字
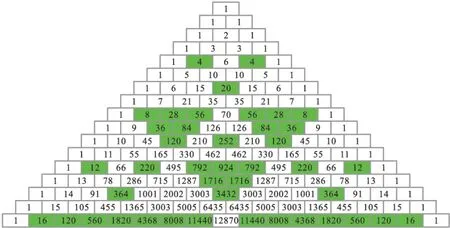
可以被4 整除的数字

可以被5 整除的数字
猜你喜欢
课堂内外·小学版(低年级)(2023年4期)2023-04-29 00:44:03
动漫星空(兴趣百科)(2020年10期)2020-10-26 06:43:22
中学生数理化(高中版.高二数学)(2019年5期)2019-06-05 08:35:54
中等数学(2018年2期)2018-08-01 06:41:36
小天使·一年级语数英综合(2018年1期)2018-06-22 10:05:16
数学小灵通·3-4年级(2016年6期)2016-04-11 08:05:30
今古传奇·故事版(2015年13期)2015-05-30 00:04:47
河南教育学院学报(自然科学版)(2015年1期)2015-03-27 06:15:11
山东理工大学学报(自然科学版)(2013年4期)2013-12-18 03:22:14
伴侣(2013年9期)2013-04-29 00:44:03

