运用“待定系数法”求解多项式新定义考题

文／盛正才

新定义考题是近年来各地中考的高频题型。本文选取一道与多项式有关的新定义考题，和大家谈谈“待定系数法”在解决这类问题中的作用。

例题对于代数式，不同的表达形式能表现出它的不同性质。例如代数式A=x2-6x+11，若将其写成A=（x-3）2+2 的形式，就能看出该多项式有最小值是2；若将它写成A=（x-1）2-4（x-1）+6 的形式，就能与代数式B=x2-4x+6建立联系。下面我们改变x的值，研究A、B两个代数式取值的规律：

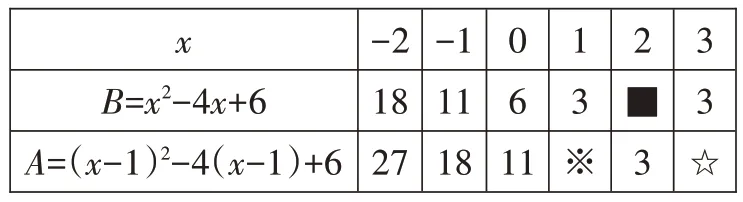
（1）表中※=____，■=____，☆=____。

（2）观察表格可以发现：若x=m时，B=x2-4x+6=n，则x=m+1 时，A=（x-1）2-4（x-1）+6=x2-6x+11=n。我们把这种现象称为代数式A参照代数式B取值后移，此时后移值为1。

①若代数式C参照代数式B取值后移，相应的后移值为2，求代数式C；

②已知代数式ax2-7x+2b参照代数式2x2-3x+c取值后移，求出a+2b-c的值。

【简答】（1）6，2，2。

（2）①C=（x-2）2-4（x-2）+6=x2-8x+18。

②设后移值为m。由题意知，a=2。

2（x-m）2-3（x-m）+c=2x2-7x+2b。

2x2+（-4m-3）x+2m2+3m+c=2x2-7x+2b。

解得m=1，2b-c=5。

∴a+2b-c=7。

【解后回顾】本例题的本质是多项式的变形，解题的关键是灵活运用待定系数法。现在来看这道新定义题的简化问题。

【简化问题】用（x+1）幂的形式表示多项式x2+4x-2。

【分析】可先设x2+4x-2=（x+1）2+p（x+1）+q，进一步求p、q的值，有两种不同的思路。

思路1：将（x+1）2+p（x+1）+q展开，得x2+（2+p）x+p+q+1，将各项系数对应起来，可得到关于p、q的方程组。p+2=4，p+q+1=-2，解得p=2，q=-5，即x2+4x-2=（x+1）2+2（x+1）-5。

思路2：将x取特殊值0、-1，可得-2=1+p+q，-5=q，解得p=2，q=-5。

【变式】若x=m时，B=x2-4x+7=n，则x=m+2 时，A=x2-8x+19=n。我们把这种现象称为代数式A参照代数式B取值延后，此时延后值为2。

（1）若代数式D参照代数式B取值延后，相应的延后值为1，请直接写出代数式D；

（2）已知代数式ax2-12x+b参照代数式2x2-4x+c取值延后，求c-b的值。

【简答】（1）∵代数式D参照代数式B取值延后，相应的延后值为1，

∴D=（x-1）2-4（x-1）+7=x2-6x+12。

（2）2x2-12x+b=2（x-m）2-4（x-m）+c，

∴4+4m=12，解得m=2。

∴b=2m2+4m+c。

∴c-b=-16。